6.2: Використання властивостей множення показників
- Page ID
- 58980
До кінця цього розділу ви зможете:
- Спрощення виразів за допомогою експонентів
- Спрощення виразів за допомогою властивості продукту для експонентів
- Спрощення виразів за допомогою властивості Power для експонентів
- Спрощення виразів за допомогою продукту до властивості живлення
- Спрощення виразів за допомогою застосування декількох властивостей
- Множення мономіалів
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спрощення:\(\frac{3}{4}\cdot \frac{3}{4}\)
Якщо ви пропустили цю проблему, перегляньте Вправу 1.6.13. - Спростити:\((−2)(−2)(−2)\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.5.13.
Спрощення виразів за допомогою експонентів
Пам'ятайте, що показник вказує на повторне множення однієї і тієї ж величини. Наприклад,\(2^4\) означає добуток\(4\) факторів\(2\), значить\(2^4\) значить\(2·2·2·2\).
Давайте розглянемо словниковий запас для виразів з показниками.
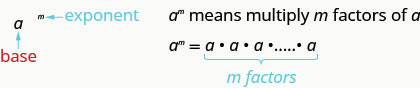
Це\(a\) читається\(m^{th}\) владі.
У\(a^{m}\) виразі показник\(m\) вказує нам, скільки разів ми використовуємо базу a як фактор.

Перш ніж ми почнемо працювати зі змінними виразами, що містять експоненти, давайте спростимо кілька виразів, що включають тільки числа.
Спростити:
- \(4^{3}\)
- \(7^{1}\)
- \(\left(\frac{5}{6}\right)^{2}\)
- \((0.63)^{2}\)
- Відповідь
-
- \(\begin{array}{ll} & 4^{3}\\ {\text { Multiply three factors of } 4 .} & {4 \cdot 4 \cdot 4} \\ {\text { Simplify. }} & {64}\end{array}\)
- \(\begin{array}{ll} & 7^{1}\\ \text{Multiply one factor of 7.} & 7\end{array}\)
- \(\begin{array}{ll} &\left(\frac{5}{6}\right)^{2}\\ {\text { Multiply two factors. }} & {\left(\frac{5}{6}\right)\left(\frac{5}{6}\right)} \\ {\text { Simplify. }} & {\frac{25}{36}}\end{array}\)
- \(\begin{array}{ll} &(0.63)^{2}\\ {\text { Multiply two factors. }} & {(0.63)(0.63)} \\ {\text { Simplify. }} & {0.3969}\end{array}\)
Спростити:
- \(6^{3}\)
- \(15^{1}\)
- \(\left(\frac{3}{7}\right)^{2}\)
- \((0.43)^{2}\)
- Відповідь
-
- 216
- 15
- \(\frac{9}{49}\)
- 0,1849
Спростити:
- \(2^{5}\)
- \(21^{1}\)
- \(\left(\frac{2}{5}\right)^{3}\)
- \((0.218)^{2}\)
- Відповідь
-
- 32
- 21
- \(\frac{8}{125}\)
- 0.047524
Спростити:
- \((-5)^{4}\)
- \(-5^{4}\)
- Відповідь
-
- \(\begin{array}{ll} &(-5)^{4}\\{\text { Multiply four factors of }-5} & {(-5)(-5)(-5)} \\ {\text { Simplify. }} & {625}\end{array}\)
- \(\begin{array}{ll} &-5^{4}\\{\text { Multiply four factors of } 5 .} & {-(5 \cdot 5 \cdot 5 \cdot 5)} \\ {\text { Simplify. }} & {-625}\end{array}\)
Зверніть увагу на подібності та відмінності в прикладі\(\PageIndex{4}\) частини 1 і Приклад\(\PageIndex{4}\) частини 2! Чому відповіді різні? Коли ми стежимо за порядком операцій у частині 1, дужки говорять нам про те,\((−5)\) щоб підняти їх до 4-ї потужності. У частині 2 ми піднімаємо якраз\(5\) до 4-ї потужності, а потім приймаємо протилежну.
Спростити:
- \((-3)^{4}\)
- \(-3^{4}\)
- Відповідь
-
- 81
- −81
Спростити:
- \((-13)^{4}\)
- \(-13^{4}\)
- Відповідь
-
- 169
- −169
Спрощення виразів за допомогою властивості продукту для експонентів
Ви бачили, що коли ви комбінуєте подібні терміни шляхом додавання та віднімання, вам потрібно мати однакову базу з однаковим показником. Але коли ви множите і ділите, показники можуть бути різними, а іноді основи можуть бути різними, теж.
Ми виведемо властивості експонентів, шукаючи шаблони в декількох прикладах.
Для початку ми розглянемо приклад, який веде до Product Product Property.
 |
|
| Що це означає? Скільки факторів взагалі? |
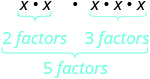 |
| Отже, у нас є | 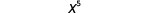 |
| Зверніть увагу, що 5 - це сума показників, 2 і 3. | 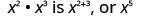 |
Пишемо:\[\begin{array}{c}{x^{2} \cdot x^{3}} \\ {x^{2+3}} \\ {x^{5}}\end{array}\]
База залишилася такою ж, і ми додали експоненти. Це призводить до властивості продукту для експонентів.
Якщо\(a\) є дійсним числом,\(m\) і\(n\) підраховують числа, то
\[a^{m} \cdot a^{n}=a^{m+n}\]
Щоб помножити з подібними основами, додайте показники.
Приклад з цифрами допомагає перевірити цю властивість.
\[\begin{array}{rll} {2^3\cdot2^2} &\stackrel{?}{=} & 2^{2+3}\\ {4\cdot 8} &\stackrel{?}{=} & 2^{5} \\ {32} &=& 32\checkmark\end{array}\]
Спростити:\(y^{5} \cdot y^{6}\)
- Відповідь
-
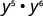
Використовувати властивість продукту,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Спростити. 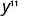
Спростити:\(b^{9} \cdot b^{8}\)
- Відповідь
-
\(b^{17}\)
Спростити:\(x^{12} \cdot x^{4}\)
- Відповідь
-
\(x^{16}\)
Спростити:
- \(2^{5} \cdot 2^{9}\)
- \(3\cdot 3^{4}\)
- Відповідь
-
а.

Використовувати властивість продукту,\(a^{m} \cdot a^{n}=a^{m+n}\). 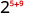
Спростити. 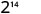
б.
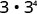
Використовувати властивість продукту,\(a^{m} \cdot a^{n}=a^{m+n}\). 
Спростити. 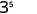
Спростити:
- \(5\cdot 5^{5}\)
- \(4^{9} \cdot 4^{9}\)
- Відповідь
-
- \(5^{6}\)
- \(4^{18}\)
Спростити:
- \(7^{6} \cdot 7^{8}\)
- \(10 \cdot 10^{10}\)
- Відповідь
-
- \(7^{14}\)
- \(10^{11}\)
Спростити:
- \(a^{7} \cdot a\)
- \(x^{27} \cdot x^{13}\)
- Відповідь
-
а.
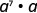
Рерайт,\(a = a^1\) 
Використовувати властивість продукту,\(a^m\cdot a^n = a^{m+n}\). 
Спростити. 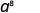
б.

Зверніть увагу, основи однакові, тому додайте експоненти. 
Спростити. 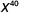
Спростити:
- \(p^{5} \cdot p\)
- \(y^{14} \cdot y^{29}\)
- Відповідь
-
- \(p^{6}\)
- \(y^{43}\)
Спростити:
- \(z \cdot z^{7}\)
- \(b^{15} \cdot b^{34}\)
- Відповідь
-
- \(z^{8}\)
- \(b^{49}\)
Ми можемо розширити властивість продукту для експонентів до більш ніж двох факторів.
Спростити:\(d^{4} \cdot d^{5} \cdot d^{2}\)
- Відповідь
-
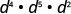
Додайте експоненти, оскільки основи однакові. 
Спростити. 
Спростити:\(x^{6} \cdot x^{4} \cdot x^{8}\)
- Відповідь
-
\(x^{18}\)
Спростити:\(b^{5} \cdot b^{9} \cdot b^{5}\)
- Відповідь
-
\(b^{19}\)
Спрощення виразів за допомогою властивості влади для експонентів
Тепер давайте розглянемо експоненціальний вираз, який містить владу, підняту до влади. Подивіться, чи зможете ви відкрити загальну власність.
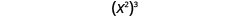 |
|
| Що це означає? Скільки факторів взагалі? |
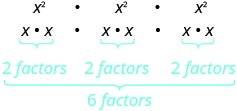 |
| Отже, у нас є | 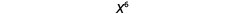 |
| Зверніть увагу, що 6 є добутком показників, 2 і 3. | 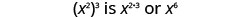 |
Пишемо:
\[\begin{array}{c}{\left(x^{2}\right)^{3}} \\ {x^{2 \cdot 3}} \\ {x^{6}}\end{array}\]
Ми помножили показники. Це призводить до властивості влади для експонентів.
Якщо\(a\) є дійсним числом, а\(m\) і\(n\) є цілими числами, то
\[\left(a^{m}\right)^{n}=a^{m \cdot n}\]
Щоб підняти силу до сили, помножте показники.
Приклад з цифрами допомагає перевірити цю властивість.
\[\begin{array} {lll} \left(3^{2}\right)^{3} &\stackrel{?}{=}&3^{2 \cdot 3} \\(9)^{3} &\stackrel{?}{=} & 3^{6} \\ 729 &=&729\checkmark \end{array}\]
Спростити:
- \(\left(y^{5}\right)^{9}\)
- \(\left(4^{4}\right)^{7}\)
- Відповідь
-
а.
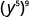
Використовуйте властивість влади,\(\big(a^m\big)^n = a^{m\cdot n}\). 
Спростити. 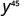
б.
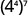
Використовуйте властивість power. 
Спростити. 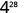
Спростити:
- \( \left(b^{7}\right)^{5} \)
- \(\left(5^{4}\right)^{3}\)
- Відповідь
-
- \( b^{35}\)
- \(5^{12}\)
Спростити:
- \(\left(z^{6}\right)^{9}\)
- \(\left(3^{7}\right)^{7}\)
- Відповідь
-
- \(z^{54}\)
- \(3^{49}\)
Спрощення виразів за допомогою продукту до властивості живлення
Зараз ми розглянемо вираз, що містить продукт, який піднятий до влади. Чи можете ви знайти цю закономірність?
\(\begin{array}{ll}{\text { What does this mean? }} & {\text { (2x) }^{3}} \\ {\text { We group the like factors together. }} & {2 x \cdot 2 x \cdot 2 x} \\ {\text { How many factors of } 2 \text { and of } x ?} & {2 \cdot 2 \cdot x^{3}} \\ {\text { Notice that each factor was raised to the power and }(2 x)^{3} \text { is } 2^{3} \cdot x^{3}}\end{array}\)
\(\begin{array}{ll}\text{We write:} & {(2 x)^{3}} \\ & {2^{3} \cdot x^{3}}\end{array}\)
Показник застосовується до кожного з факторів! Це призводить до продукту до властивості влади для експонентів.
Якщо\(a\) і\(b\) є дійсними числами і\(m\) є цілим числом, то
\[(a b)^{m}=a^{m} b^{m}\]
Щоб підняти продукт до влади, підніміть кожен фактор до цієї сили.
Приклад з цифрами допомагає перевірити це властивість:
\ [\ begin {масив} {lll} (2\ dot 3) ^ {2} &\ стекер {?} {=} &2^ {2}\ крапка 3^ {2}\\ 6^ {2} &\ стекер {?} {=} &4\ cdot 9\\ 36 &=&36
\ галочка\ кінець {масив}\]
Спростити:
- \((-9 d)^{2}\)
- \((3mn)^{3}\).
- Відповідь
-
а.
б.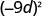
Використовувати силу властивості продукту,\((ab)^m=a^m b^m\). 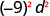
Спростити. 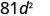
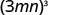
Використовувати силу властивості продукту,\((ab)^m=a^m b^m\). 
Спростити. 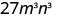
Спростити:
- \((-12 y)^{2}\)
- \((2 w x)^{5}\)
- Відповідь
-
- \(144y^{2}\)
- \(32w^{5} x^{5}\)
Спростити:
- \((5 w x)^{3}\)
- \((-3 y)^{3}\)
- Відповідь
-
- 125\(w^{3} x^{3}\)
- \(-27 y^{3}\)
Спрощення виразів за допомогою застосування декількох властивостей
Тепер у нас є три властивості для множення виразів з показниками. Давайте підсумуємо їх, а потім ми зробимо кілька прикладів, які використовують більше одного з властивостей.
Якщо\(a\) і\(b\) є дійсними числами, а\(m\) і\(n\) є цілими числами, то
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
Усі властивості експоненти мають значення true для будь-яких дійсних чисел\(m\) і\(n\). Зараз ми використовуємо лише цілі показники кількості.
Спростити:
- \(\left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\)
- \(\left(-6 x^{4} y^{5}\right)^{2}\)
- Відповідь
-
- \(\begin{array}{ll}& \left(y^{3}\right)^{6}\left(y^{5}\right)^{4}\\ {\text { Use the Power Property. }}& y^{18} \cdot y^{20} \\ {\text { Add the exponents. }} & y^{38} \end{array}\)
- \(\begin{array}{ll}& \left(-6 x^{4} y^{5}\right)^{2}\\ {\text { Use the Product to a Power Property. }} & {(-6)^{2}\left(x^{4}\right)^{2}\left(y^{5}\right)^{2}} \\ {\text { Use the Power Property. }} & {(-6)^{2}\left(x^{8}\right)\left(y^{10}\right)^{2}} \\ {\text { Simplify. }} & {36 x^{8} y^{10}}\end{array}\)
Спростити:
- \(\left(a^{4}\right)^{5}\left(a^{7}\right)^{4}\)
- \(\left(-2 c^{4} d^{2}\right)^{3}\)
- Відповідь
-
- \(a^{48}\)
- \(-8 c^{12} d^{6}\)
Спростити:
- \(\left(-3 x^{6} y^{7}\right)^{4}\)
- \(\left(q^{4}\right)^{5}\left(q^{3}\right)^{3}\)
- Відповідь
-
- 81\(x^{24} y^{28}\)
- \(q^{29}\)
Спростити:
- \((5 m)^{2}\left(3 m^{3}\right)\)
- \(\left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3}\)
- Відповідь
-
- \(\begin{array}{ll}& (5 m)^{2}\left(3 m^{3}\right)\\{\text { Raise } 5 m \text { to the second power. }} & {5^{2} m^{2} \cdot 3 m^{3}} \\ {\text { Simplify. }} & {25 m^{2} \cdot 3 m^{3}} \\ {\text { Use the Commutative Property. }} & {25 \cdot 3 \cdot m^{2} \cdot m^{3}} \\ {\text { Multiply the constants and add the exponents. }} & {75 m^{5}}\end{array}\)
- \(\begin{array}{ll} & \left(3 x^{2} y\right)^{4}\left(2 x y^{2}\right)^{3} \\ \text{Use the Product to a Power Property.} & \left(3^{4} x^{8} y^{4}\right)\left(2^{3} x^{3} y^{6}\right)\\\text{Simplify.} & \left(81 x^{8} y^{4}\right)\left(8 x^{3} y^{6}\right)\\ \text{Use the Commutative Property.} &81\cdot 8 \cdot x^{8} \cdot x^{3} \cdot y^{4} \cdot y^{6} \\\text{Multiply the constants and add the exponents.} & 648x^{11} y^{10}\\ \end{array}\)
Спростити:
- \((5 n)^{2}\left(3 n^{10}\right)\)
- \(\left(c^{4} d^{2}\right)^{5}\left(3 c d^{5}\right)^{4}\)
- Відповідь
-
- 75\(n^{12}\)
- 81\(c^{24} d^{30}\)
Спростити:
- \(\left(a^{3} b^{2}\right)^{6}\left(4 a b^{3}\right)^{4}\)
- \((2 x)^{3}\left(5 x^{7}\right)\)
- Відповідь
-
- 256\(a^{22} b^{24}\)
- 40\(x^{10}\)
Множення мономіалів
Оскільки мономіал - це алгебраїчний вираз, ми можемо використовувати властивості експонент для множення мономов.
Помножити:\(\left(3 x^{2}\right)\left(-4 x^{3}\right)\)
- Відповідь
-
\ (\ begin {масив} {ll} &\ left (3 x^ {2}\ праворуч)\ left (-4 x^ {3}\ right)\\ text {Використовуйте комутативну властивість для перестановки термінів.} & 3\ cdot (-4)\ cdot x^ {2}\ cdot x^ {3}\
\ текст {Множення.} & -12 x^ {5}\ кінець {масив}\)
Помножити:\(\left(5 y^{7}\right)\left(-7 y^{4}\right)\)
- Відповідь
-
\(-35 y^{11}\)
Помножити:\(\left(-6 b^{4}\right)\left(-9 b^{5}\right)\)
- Відповідь
-
54\(b^{9}\)
Помножити:\(\left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\)
- Відповідь
-
\(\begin{array}{ll} & \left(\frac{5}{6} x^{3} y\right)\left(12 x y^{2}\right)\\ \text{Use the Commutative Property to rearrange the terms.} & \frac{5}{6} \cdot 12 \cdot x^{3} \cdot x \cdot y \cdot y^{2}\\ \text{Multiply.} &10x^{4} y^{3}\end{array}\)
Помножити:\(\left(\frac{2}{5} a^{4} b^{3}\right)\left(15 a b^{3}\right)\)
- Відповідь
-
6\(a^{5} b^{6}\)
Помножити:\(\left(\frac{2}{3} r^{5} s\right)\left(12 r^{6} s^{7}\right)\)
- Відповідь
-
8\(r^{11} s^{8}\)
Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики з використанням властивостей множення показників:
- Властивості множення показників
Ключові концепції
- Експоненціальне позначення
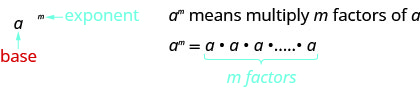
- Властивості експонентів
- Якщо\(a\) і\(b\) є дійсними числами і\(m\) і\(n\) є цілими числами, то
\[\begin{array}{llll} \textbf{Product Property } & a^{m} \cdot a^{n}&=&a^{m+n} \\ \textbf {Power Property } &\left(a^{m}\right)^{n}&=&a^{m n} \\ \textbf {Product to a Power } &(a b)^{m}&=&a^{m} b^{m} \end{array}\]
