6.5: Розділити мономи
- Page ID
- 58982
До кінця цього розділу ви зможете:
- Спрощення виразів за допомогою властивості частки для експонентів
- Спрощення виразів з нульовими показниками
- Спрощення виразів за допомогою коефіцієнта до властивості живлення
- Спрощення виразів за допомогою застосування декількох властивостей
- Розділити мономи
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Спростити:\(\dfrac{8}{24}\).
Якщо ви пропустили цю проблему, перегляньте Вправа 1.6.4. - Спростити:\((2m^3)^5\).
Якщо ви пропустили цю проблему, перегляньте Вправа 6.2.22. - Спрощення:\(\dfrac{12x}{12y}\)
Якщо ви пропустили цю проблему, перегляньте Вправу 1.6.10.
Спрощення виразів за допомогою властивості частки для експонентів
Раніше в цьому розділі ми розробили властивості експонент для множення. Ми підсумуємо ці властивості нижче.
Якщо a і b є дійсними числами, а m і n - цілими числами, то
\[\begin{array}{ll}{\textbf { Product Property }} & {a^{m} \cdot a^{n}=a^{m+n}} \\ {\textbf { Power Property }} & {\left(a^{m}\right)^{n}=a^{m n}} \\ {\textbf { Product to a Power }} & {(a b)^{m}=a^{m} b^{m}}\end{array}\]
Тепер ми розглянемо властивості показника для ділення. Швидке оновлення пам'яті може допомогти, перш ніж ми почнемо роботу. Ви навчилися спрощувати дроби, діливши загальні множники з чисельника та знаменника за допомогою властивості еквівалентних дробів. Ця властивість також допоможе вам працювати з алгебраїчними дробами, які також є частками.
Якщо a, b і c - цілі числа де\(b\neq 0,c\neq 0\).
\[\text{then} \quad \dfrac{a}{b}=\dfrac{a \cdot c}{b \cdot c} \quad \text{and} \quad \dfrac{a \cdot c}{b \cdot c}=\dfrac{a}{b}\]
Як і раніше, ми спробуємо виявити нерухомість, розглянувши деякі приклади.
\[\begin{array}{lclc}{\text { Consider }} & \dfrac{x^{5}}{x^{2}} & \text{and} & \dfrac{x^{2}}{x^{3}}\\ {\text { What do they mean? }}&\dfrac{x \cdot x \cdot x \cdot x \cdot x}{x \cdot x} && \dfrac{x \cdot x}{x \cdot x \cdot x}\\ {\text { Use the Equivalent Fractions Property. }} & {\dfrac{x \not\cdot x \not\cdot x \cdot x \cdot x}{x \not\cdot\not x}} && \dfrac{\not x \cdot\not x \cdot 1}{x \not \cdot\not x \cdot x}\\ {\text { Simplify. }} & {x^{3}} & & \dfrac{1}{x}\end{array}\]
Зверніть увагу, в кожному випадку основи були однаковими, і ми віднімали показники.
Коли більший показник був у чисельнику, ми залишилися з множниками в чисельнику.
Коли більший показник був у знаменнику, ми залишилися з факторами в знаменнику - зверніть увагу на чисельник 1.
Пишемо:
\[\begin{array}{cc}{\dfrac{x^{5}}{x^{2}}} & {\dfrac{x^{2}}{x^{3}}} \\ {x^{5-2}} & {\dfrac{1}{x^{3-2}}} \\ {x^{3}} & {\dfrac{1}{x}}\end{array}\]
Це призводить до частки властивість для експонентів.
Якщо a - дійсне число\(a\neq 0\), а m і n - цілі числа, то
\[\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}, n>m\]
Пара прикладів з цифрами може допомогти перевірити цю властивість.
\[\begin{array} {llllll} \dfrac{3^{4}}{3^{2}} &=&3^{4-2}& \dfrac{5^{2}}{5^{3}} &=&\dfrac{1}{5^{3-2}} \\ \dfrac{81}{9} &=&3^{2} & \dfrac{25}{125} &=&\dfrac{1}{5^{1}} \\ 9 &=&9\checkmark& \dfrac{1}{5} &=&\dfrac{1}{5} \checkmark \end{array}\]
Спростити:
- \(\dfrac{x^{9}}{x^{7}}\)
- \(\dfrac{3^{10}}{3^{2}}\)
- Відповідь
-
Щоб спростити вираз з часткою, нам потрібно спочатку порівняти показники в чисельнику і знаменнику.
1.
Починаючи з 9 > 7, є більше множників х в чисельнику. 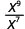
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 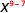
Спростити. \(x^2\) 2.
Зверніть увагу, що коли більший показник знаходиться в чисельнику, ми залишаємося з множниками в чисельнику.Починаючи з 10 > 2, є більше множників х в чисельнику. 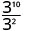
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=a^{m-n}\) 
Спростити. \(3^8\)
Спростити:
- \(\dfrac{x^{15}}{x^{10}}\)
- \(\dfrac{6^{14}}{6^{5}}\)
- Відповідь
-
- \(x^{5}\)
- \(6^9\)
Спростити:
- \(\dfrac{y^{43}}{y^{37}}\)
- \(\dfrac{10^{15}}{10^{7}}\)
- Відповідь
-
- \(y^{6}\)
- \(10^8\)
Спростити:
- \(\dfrac{b^{8}}{b^{12}}\)
- \(\dfrac{7^{3}}{7^{5}}\)
- Відповідь
-
Щоб спростити вираз з часткою, нам потрібно спочатку порівняти показники в чисельнику і знаменнику.
1.
Починаючи з 12 > 8, в знаменнику більше факторів b. 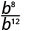
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 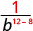
Спростити. 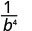
2.
Зверніть увагу, що коли більший показник знаходиться в знаменнику, ми залишаємося з факторами в знаменнику.Починаючи з 5 > 3, в знаменнику більше факторів 3. 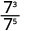
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 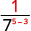
Спростити. 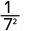
Спростити. 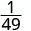
Спростити:
- \(\dfrac{x^{18}}{x^{22}}\)
- \(\dfrac{12^{15}}{12^{30}}\)
- Відповідь
-
- \(\dfrac{1}{x^{4}}\)
- \(\dfrac{1}{12^{15}}\)
Спростити:
- \(\dfrac{m^{7}}{m^{15}}\)
- \(\dfrac{9^{8}}{9^{19}}\)
- Відповідь
-
- \(\dfrac{1}{m^{8}}\)
- \(\dfrac{1}{9^{11}}\)
Зверніть увагу на різницю в двох попередніх прикладах:
- Якщо ми почнемо з більшої кількості факторів у чисельнику, ми закінчимо множниками в чисельнику.
- Якщо ми почнемо з більшої кількості факторів у знаменнику, ми закінчимо множниками в знаменнику.
Першим кроком у спрощенні виразу за допомогою Коефіцієнтної властивості для експонентів є визначення того, чи є показник більшим у чисельнику або знаменнику.
Спростити:
- \(\dfrac{a^{5}}{a^{9}}\)
- \(\dfrac{x^{11}}{x^{7}}\)
- Відповідь
-
1. Чи є експонентою більшого в чисельнику або знаменнику? Починаючи з 9 > 5, є більше а в знаменнику, і тому ми закінчимо з факторами в знаменнику.
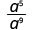
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 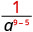
Спростити. 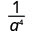
2. Зверніть увагу, що в чисельнику більше факторів xx, починаючи з 11 > 7. Таким чином, ми закінчимо з факторами в чисельнику.
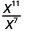
Використовуйте властивість частки,\(\dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}\) 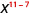
Спростити. 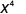
Спростити:
- \(\dfrac{b^{19}}{b^{11}}\)
- \(\dfrac{z^{5}}{z^{11}}\)
- Відповідь
-
- \(b^{8}\)
- \(\dfrac{1}{z^{6}}\)
Спростити:
- \(\dfrac{p^{9}}{p^{17}}\)
- \(\dfrac{w^{13}}{w^{9}}\)
- Відповідь
-
- \(\dfrac{1}{p^{8}}\)
- \(w^{4}\)
Спрощення виразів з показником нуля
Особливий випадок часткового властивості - це коли показники чисельника та знаменника рівні, наприклад, вираз на кшталт\(\dfrac{a^{m}}{a^{m}}\). З вашої попередньої роботи з дробами ви знаєте, що:
\[\dfrac{2}{2}=1 \quad \dfrac{17}{17}=1 \quad \dfrac{-43}{-43}=1\]
У словах число, розділене саме по собі, дорівнює 1. Отже, для будь-якого\(\dfrac{x}{x}=1\)\(x(x\neq 0)\), так як будь-яке число, розділене саме по собі, дорівнює 1.
Коефіцієнтна властивість для експонентів показує нам, як спростити,\(\dfrac{a^{m}}{a^{n}}\) коли\(m>n\) і коли\(n<m\), віднімаючи показники. Що робити, якщо\(m=n\)?
Розглянемо\(\dfrac{8}{8}\), який ми знаємо 1.
\(\begin{array} {lrll} & \dfrac{8}{8} &=&1 \\ \text { Write } 8 \text { as } 2^{3} . & \dfrac{2^{3}}{2^{3}} &=&1 \\ \text { Subtract exponents. } & 2^{3-3} &=&1 \\ \text { Simplify. } & 2^{0} &=&1 \end{array}\)
Тепер ми спростимо двома\(\dfrac{a^{m}}{a^{m}}\) способами, щоб привести нас до визначення нульового показника. Загалом, для\(a\neq 0\):
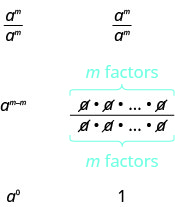
Ми бачимо\(\dfrac{a^{m}}{a^{m}}\) спрощує до\(a^{0}\) і до 1. Отже\(a^{0} = 1\).
Якщо a - ненульове число, то\(a^{0} = 1\).
Будь-яке ненульове число, підняте до нульової потужності, дорівнює 1.
У цьому тексті ми припускаємо, що будь-яка змінна, яку ми піднімаємо до нульової потужності, не дорівнює нулю.
Спростити:
- \(9^{0}\)
- \(n^{0}\)
- Відповідь
-
Визначення говорить, що будь-яке ненульове число, підняте до нульової потужності, дорівнює 1.
- \(\begin{array}{ll} & 9^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
- \(\begin{array}{ll} & n^0\\ \text{Use the definition of the zero exponent.} & 1 \end{array}\)
Спростити:
- \(15^{0}\)
- \(m^{0}\)
- Відповідь
-
- 1
- 1
Спростити:
- \(k^{0}\)
- \(29^{0}\)
- Відповідь
-
- 1
- 1
Тепер, коли ми визначили нульовий показник, ми можемо розширити всі властивості експонентів, щоб включити ціле число експонентів.
Як щодо підняття виразу до нульової потужності? Давайте подивимося на\((2x)^0\). Ми можемо використовувати продукт до правила влади, щоб переписати цей вираз.
\[\begin{array}{ll} & (2x)^0\\ {\text { Use the product to a power rule. }} & {2^{0} x^{0}} \\ {\text { Use the zero exponent property. }} & {1 \cdot 1} \\ {\text { Simplify. }} & 1\end{array}\]
Це говорить нам про те, що будь-який ненульовий вираз, піднятий до нульової потужності, є одиницею.
Спростити:
- \((5b)^0\)
- \((−4a^{2}b)^0\).
- Відповідь
-
- \(\begin{array}{ll} & (5b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
- \(\begin{array}{ll} & (−4a^{2}b)^0\\ {\text {Use the definition of the zero exponent.}} & 1\end{array}\)
Спростити:
- \((11z)^0\)
- \((−11pq^{3})^0\).
- Відповідь
-
- 1
- 1
Спростити:
- \((-6d)^0\)
- \((−8m^{2}n^{3})^0\).
- Відповідь
-
- 1
- 1
Спрощення виразів за допомогою коефіцієнта до властивості влади
Тепер ми розглянемо приклад, який приведе нас до частки до власності влади.
\[\begin{array}{lc} & {\left(\dfrac{x}{y}\right)^{3}} \\ \text{This means:} & {\dfrac{x}{y} \cdot \dfrac{x}{y} \cdot \dfrac{x}{y}} \\ \text{Multiply the fractions.} &{\dfrac{x \cdot x \cdot x}{y \cdot y \cdot y}} \\ \text{Write with exponents.} & {\dfrac{x^{3}}{y^{3}}}\end{array}\]
Зверніть увагу, що показник застосовується як до чисельника, так і до знаменника.
\[\begin{array}{lc}{\text { We see that }\left(\dfrac{x}{y}\right)^{3} \text { is } \dfrac{x^{3}}{y^{3}}} \\ {\text { We write: }} & \left(\dfrac{x}{y}\right)^{3} \\ & {\dfrac{x^{3}}{y^{3}}} \end{array}\]
Це призводить до частки до властивості влади для експонентів.
Якщо a і b є дійсними числами\(b\neq 0\), а m - рахунковим числом, то
\[\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\]
Щоб підняти дріб до степеня, підніміть чисельник і знаменник до цієї міри.
Приклад з цифрами може допомогти розібратися в цій властивості:
\[\begin{aligned}\left(\dfrac{2}{3}\right)^{3} &=\dfrac{2^{3}}{3^{3}} \\ \dfrac{2}{3} \cdot \dfrac{2}{3} \cdot \dfrac{2}{3} &=\dfrac{8}{27} \\ \dfrac{8}{27} &=\dfrac{8}{27}\checkmark \end{aligned}\]
Спростити:
- \(\left(\dfrac{3}{7}\right)^{2}\)
- \(\left(\dfrac{b}{3}\right)^{4}\)
- \(\left(\dfrac{k}{j}\right)^{3}\)
- Відповідь
-
1.
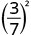
Використовуйте властивість частки,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 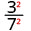
Спростити. 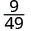
2.
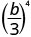
Використовуйте властивість частки,\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\) 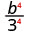
Спростити. 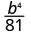
3.

Підняти чисельник і знаменник до третього ступеня. 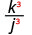
Спростити:
- \(\left(\dfrac{5}{8}\right)^{2}\)
- \(\left(\dfrac{p}{10}\right)^{4}\)
- \(\left(\dfrac{m}{n}\right)^{7}\)
- Відповідь
-
- \(\dfrac{25}{64}\)
- \(\dfrac{p^{4}}{10,000}\)
- \(\dfrac{m^{7}}{n^{7}}\)
Спростити:
- \(\left(\dfrac{1}{3}\right)^{3}\)
- \(\left(\dfrac{-2}{q}\right)^{3}\)
- \(\left(\dfrac{w}{x}\right)^{4}\)
- Відповідь
-
- \(\dfrac{1}{27}\)
- \(\dfrac{-8}{q^{3}}\)
- \(\dfrac{w^{4}}{x^{4}}\)
Спрощення виразів за допомогою застосування декількох властивостей
Тепер ми підсумуємо всі властивості експонентів, щоб вони всі разом посилатися, оскільки ми спрощуємо вирази, використовуючи кілька властивостей. Зверніть увагу, що тепер вони визначені для цілих числових показників.
Якщо a і b є дійсними числами, а m і n - цілими числами, то
\[\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\]
Спростити:\(\dfrac{\left(y^{4}\right)^{2}}{y^{6}}\)
- Відповідь
-
\(\begin{array} {ll} & \dfrac{\left(y^{4}\right)^{2}}{y^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{y^{8}}{y^{6}}\\ \text{Subtract the exponents.} &y^{2} \end{array}\)
Спростити:\(\dfrac{\left(m^{5}\right)^{4}}{m^{7}}\)
- Відповідь
-
\(m^{13}\)
Спростити:\(\dfrac{\left(k^{2}\right)^{6}}{k^{7}}\)
- Відповідь
-
\(k^{5}\)
Спростити:\(\dfrac{b^{12}}{\left(b^{2}\right)^{6}}\)
- Відповідь
-
\[\begin{array} {ll} &\dfrac{b^{12}}{\left(b^{2}\right)^{6}} \\ \text{Multiply the exponents in the numerator.} & \dfrac{b^{12}}{b^{12}}\\ \text{Subtract the exponents.} &b^{0} \\ \text{Simplify} & 1\end{array}\]
Зверніть увагу, що після того, як ми спростили знаменник на першому кроці, чисельник і знаменник були рівними. Таким чином, кінцеве значення дорівнює 1.
Спростити\(\dfrac{n^{12}}{\left(n^{3}\right)^{4}}\).
- Відповідь
-
1
Спростити\(\dfrac{x^{15}}{\left(x^{3}\right)^{5}}\).
- Відповідь
-
1
Спростити:\(\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\)
- Відповідь
-
\[\begin{array} {ll} &\left(\dfrac{y^{9}}{y^{4}}\right)^{2}\\ \text{Remember parentheses come before exponents.} &\\ \text{Notice the bases are the same, so we can simplify} &\left(y^{5}\right)^{2} \\ \text{inside the parentheses. Subtract the exponents.} & \\\text{Multiply the exponents.} &y^{10} \end{array}\]
Спростити:\(\left(\dfrac{r^{5}}{r^{3}}\right)^{4}\)
- Відповідь
-
\(r^{8}\)
Спростити:\(\left(\dfrac{v^{6}}{v^{4}}\right)^{3}\)
- Відповідь
-
\(v^{6}\)
Спростити:\(\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\)
- Відповідь
-
Тут ми не можемо спочатку спростити всередині дужок, оскільки основи не однакові.
\(\begin{array} {ll} &\left(\dfrac{j^{2}}{k^{3}}\right)^{4}\\ \text{Raise the numerator and denominator to the third power} & \\ \text{using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{\left(j^{2}\right)^{4}}{\left(k^{3}\right)^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{j^{8}}{k^{12}} \end{array}\)
Спростити:\(\left(\dfrac{a^{3}}{b^{2}}\right)^{4}\)
- Відповідь
-
\(\dfrac{a^{12}}{b^{8}}\)
Спростити:\(\left(\dfrac{q^{7}}{r^{5}}\right)^{3}\)
- Відповідь
-
\(\dfrac{q^{21}}{r^{15}}\)
Спростити:\(\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\)
- Відповідь
-
\(\begin{array} {ll} &\left(\dfrac{2 m^{2}}{5 n}\right)^{4}\\ \text{Raise the numerator and denominator to the fourth} &\dfrac{\left(2 m^{2}\right)^{4}}{(5 n)^{4}} \\ \text{power, using the Quotient to a Power Property,}\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}} &\dfrac{2^{4}\left(m^{2}\right)^{4}}{5^{4} n^{4}}\\ \text{Use the Power Property and simplify.} & \dfrac{16 m^{8}}{625 n^{4}} \end{array}\)
Спростити:\(\left(\dfrac{7 x^{3}}{9 y}\right)^{2}\)
- Відповідь
-
\(\dfrac{49 x^{6}}{81 y^{2}}\)
Спростити:\(\left(\dfrac{3 x^{4}}{7 y}\right)^{2}\)
- Відповідь
-
\(\dfrac{9 x^{8}}{49 v^{2}}\)
Спростити:\(\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\)
- Відповідь
-
\(\begin{array}{ll}&\dfrac{\left(x^{3}\right)^{4}\left(x^{2}\right)^{5}}{\left(x^{6}\right)^{5}}\\ \text{Use the Power Property,}\left(a^{m}\right)^{n}=a^{m \cdot n} &\dfrac{\left(x^{12}\right)\left(x^{10}\right)}{\left(x^{30}\right)}\\ \text{Add the exponents in the numerator.} &\dfrac{x^{22}}{x^{30}}\\ \text{Use the Quotient Property,} \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}}&\dfrac{1}{x^{8}}\end{array}\)
Спростити:\(\dfrac{\left(a^{2}\right)^{3}\left(a^{2}\right)^{4}}{\left(a^{4}\right)^{5}}\)
- Відповідь
-
\(\dfrac{1}{a^{6}}\)
Спростити:\(\dfrac{\left(p^{3}\right)^{4}\left(p^{5}\right)^{3}}{\left(p^{7}\right)^{6}}\)
- Відповідь
-
\(\dfrac{1}{p^{15}}\)
Спростити:\(\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\)
- Відповідь
-
\(\begin{array} {ll} &\dfrac{\left(10 p^{3}\right)^{2}}{(5 p)^{3}\left(2 p^{5}\right)^{4}}\\ \text { Use the Product to a Power Property, }(a b)^{m}=a^{m} b^{m}&\dfrac{(10)^{2}\left(p^{3}\right)^{2}}{(5)^{3}(p)^{3}(2)^{4}\left(p^{5}\right)^{4}}\\ \text { Use the Power Property, }\left(a^{m}\right)^{n}=a^{m \cdot n}&\dfrac{100 p^{6}}{125 p^{3} \cdot 16 p^{20}}\\ \text { Add the exponents in the denominator. }&\dfrac{100 p^{6}}{125 \cdot 16 p^{23}} \\ \text { Use the Quotient Property, } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{n-m}} & \dfrac{100}{125 \cdot 16 p^{17}} \\ \text { Simplify. } & \dfrac{1}{20 p^{17}} \end{array}\)
Спростити:\(\dfrac{\left(3 r^{3}\right)^{2}\left(r^{3}\right)^{7}}{\left(r^{3}\right)^{3}}\)
- Відповідь
-
9\(r^{18}\)
Спростити:\(\dfrac{\left(2 x^{4}\right)^{5}}{\left(4 x^{3}\right)^{2}\left(x^{3}\right)^{5}}\)
- Відповідь
-
\(\dfrac{2}{x}\)
Розділити мономи
Тепер ви ознайомилися з усіма властивостями експонентів і використовували їх для спрощення виразів. Далі ви побачите, як використовувати ці властивості для поділу мономов. Пізніше ви будете використовувати їх для поділу многочленів.
Знайдіть частку:\(56 x^{7} \div 8 x^{3}\)
- Відповідь
-
\[\begin{array} {ll} &56 x^{7} \div 8 x^{3}\\ \text { Rewrite as a fraction. }&\dfrac{56 x^{7}}{8 x^{3}}\\ \text { Use fraction multiplication. }&\dfrac{56}{8} \cdot \dfrac{x^{7}}{x^{3}}\\ \text { Simplify and use the Quotient Property. }&7 x^{4}\end{array}\]
Знайдіть частку:\(42y^{9} \div 6 y^{3}\)
- Відповідь
-
\(7y^{6}\)
Знайдіть частку:\(48z^{8} \div 8 z^{2}\)
- Відповідь
-
\(6z^{6}\)
Знайдіть частку:\(\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\)
- Відповідь
-
Коли ми ділимо мономіали з більш ніж однією змінною, ми пишемо один дріб для кожної змінної.
\(\begin{array} {ll} &\dfrac{45 a^{2} b^{3}}{-5 a b^{5}}\\ \text { Use fraction multiplication. }&\dfrac{45}{-5} \cdot \dfrac{a^{2}}{a} \cdot \dfrac{b^{3}}{b^{5}}\\\text { Simplify and use the Quotient Property. }&-9 \cdot a \cdot \dfrac{1}{b^{2}}\\\text { Multiply. }&-\dfrac{9 a}{b^{2}}\end{array}\)
Знайдіть частку:\(\dfrac{-72 a^{7} b^{3}}{8 a^{12} b^{4}}\)
- Відповідь
-
\(-\dfrac{9}{a^{5} b}\)
Знайдіть частку:\(\dfrac{-63 c^{8} d^{3}}{7 c^{12} d^{2}}\)
- Відповідь
-
\(\dfrac{-9 d}{c^{4}}\)
Знайдіть частку:\(\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\)
- Відповідь
-
\(\begin{array} {ll} &\dfrac{24 a^{5} b^{3}}{48 a b^{4}}\\ \text { Use fraction multiplication. }&\dfrac{24}{48} \cdot \dfrac{a^{5}}{a} \cdot \dfrac{b^{3}}{b^{4}}\\\text { Simplify and use the Quotient Property. }&\dfrac{1}{2} \cdot a^{4} \cdot \dfrac{1}{b}\\\text { Multiply. }&\dfrac{a^{4}}{2 b}\end{array}\)
Знайдіть частку:\(\dfrac{16 a^{7} b^{6}}{24 a b^{8}}\)
- Відповідь
-
\(\dfrac{2 a^{6}}{3 b^{2}}\)
Знайдіть частку:\(\dfrac{27 p^{4} q^{7}}{-45 p^{12} q}\)
- Відповідь
-
\(-\dfrac{3 q^{6}}{5 p^{8}}\)
Після того, як ви ознайомитеся з процесом і практикуєте його крок за кроком кілька разів, ви можете спростити частку за один крок.
Знайдіть частку:\(\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\)
- Відповідь
-
Будьте дуже обережні, щоб спростити,\(\dfrac{14}{21}\) розділивши загальний коефіцієнт, і спростити змінні, віднімаючи їх показники.
\(\begin{array} {ll} &\dfrac{14 x^{7} y^{12}}{21 x^{11} y^{6}}\\ \text { Simplify and use the Quotient Property. } & \dfrac{2 y^{6}}{3 x^{4}}\end{array}\)
Знайдіть частку:\(\dfrac{28 x^{5} y^{14}}{49 x^{9} y^{12}}\)
- Відповідь
-
\(\dfrac{4 y^{2}}{7 x^{4}}\)
Знайдіть частку:\(\dfrac{30 m^{5} n^{11}}{48 m^{10} n^{14}}\)
- Відповідь
-
\(\dfrac{5}{8 m^{5} n^{3}}\)
У всіх прикладах досі не було роботи в чисельнику або знаменнику перед спрощенням дробу. У наступному прикладі ми спочатку знайдемо добуток двох мономов у чисельнику, перш ніж спростити дріб. Це випливає за порядком операцій. Пам'ятайте, що смужка дробу - це символ угруповання.
Знайдіть частку:\(\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\)
- Відповідь
-
\(\begin{array} {lc} &\dfrac{\left(6 x^{2} y^{3}\right)\left(5 x^{3} y^{2}\right)}{\left(3 x^{4} y^{5}\right)}\\ \text { Simplify the numerator. }&\dfrac{30 x^{5} y^{5}}{3 x^{4} y^{5}} \\ \text { Simplify. } &10 x \end{array}\)
Знайдіть частку:\(\dfrac{\left(6 a^{4} b^{5}\right)\left(4 a^{2} b^{5}\right)}{12 a^{5} b^{8}}\)
- Відповідь
-
\(2 a b^{2}\)
Знайдіть частку:\(\dfrac{\left(-12 x^{6} y^{9}\right)\left(-4 x^{5} y^{8}\right)}{-12 x^{10} y^{12}}\)
- Відповідь
-
\(-4 x y^{5}\)
Отримайте доступ до цих онлайн-ресурсів для додаткового навчання та практики з розділенням мономій:
- Раціональні вирази
- Розділення мономов
- Розділення мономов 2
Ключові поняття
- Частота властивість для експонентів:
- Якщо a - дійсне число\(a\neq 0\), а m, n - цілі числа, то:\(\dfrac{a^{m}}{a^{n}}=a^{m-n}, m>n \text { and } \dfrac{a^{m}}{a^{n}}=\dfrac{1}{a^{m-n}}, n>m\)
- Нульовий показник
- Якщо a - ненульове число, то\(a^{0} =1\).
- Коефіцієнт до властивості влади для експонентів:
- Якщо a і b є дійсними числами\(b\neq 0\), а mm - рахунковим числом, то:\(\left(\dfrac{a}{b}\right)^{m}=\dfrac{a^{m}}{b^{m}}\)
- Щоб підняти дріб до степеня, підніміть чисельник і знаменник до цієї міри.
- Резюме властивостей експоненти
- Якщо a, b - дійсні числа, а m, nm, n - цілі числа, то\(\begin{array}{lrll} \textbf{Product Property} & a^{m} \cdot a^{n} &=&a^{m+n} \\\textbf{Power Property} & \left(a^{m}\right)^{n} &=&a^{m \cdot n} \\\textbf{Product to a Power} & (a b)^{m} &=&a^{m} b^{m} \\ \textbf{Quotient Property} & \dfrac{a^{m}}{a^{n}} &=&a^{m-n}, a \neq 0, m>n \\ & \dfrac{a^{n}}{a^{n}} &=&1, a \neq 0, n>m \\\textbf{Zero Exponent Definition} &a^0&=&1,a\neq 0 \\\textbf{Quotient to a Power Property} & \left(\dfrac{a}{b}\right)^{m} &=&\dfrac{a^{m}}{b^{m}}, b \neq 0 \end{array}\)
