6.4E: Вправи

Практика робить досконалим

Квадрат біном з використанням візерунка біноміальних квадратів

У наступних вправах, квадрат кожного бічлена за допомогою біноміальних квадратів візерунок.

Вправа 1

$(w+4)^2$

Вправа 2

$(q+12)^2$

Відповідь

$q^2+24q+144$

Вправа 3

$(y+14)^2$

Вправа 4

$(x+\frac{2}{3})^2$

Відповідь

$x^2+\frac{4}{3}x+\frac{4}{9}$

Вправа 5

$(b−7)^2$

Вправа 6

$(y−6)^2$

Відповідь

$y^2−12y+36$

Вправа 7

$(m−15)^2$

Вправа 8

$(p−13)^2$

Відповідь

$p^2−26p+169$

Вправа 9

$(3d+1)^2$

Вправа 10

$(4a+10)^2$

Відповідь

$16a^2+80a+100$

Вправа 11

$(2q+13)^2$

Вправа 12

$(3z+15)^2$

Відповідь

$9z^2+65z+125$

Вправа 13

$(3x−y)^2$

Вправа 14

$(2y−3z)^2$

Відповідь

$4y^2−12yz+9z^2$

Вправа 15

$(15x−17y)^2$

Вправа 16

$(18x−19y)^2$

Відповідь

$164x^2−136xy+181y^2$

Вправа 17

$(3x2+2)^2$

Вправа 18

$(5u^2+9)^2$

Відповідь

$25u^4+90u^2+81$

Вправа 19

$(4y^3−2)^2$

Вправа 20

$(8p^3−3)^2$

Відповідь

$64p^6−48p^3+9$

Множення кон'югатів за допомогою добутку візерунка кон'югатів

У наступних вправах помножте кожну пару кон'югатів, використовуючи візерунок «Твір кон'югатів».

Вправа 21

$(m−7)(m+7)$

Вправа 22

$(c−5)(c+5)$

Відповідь

$c^2−25$

Вправа 23

$(x+34)(x−34)$

Вправа 24

$(b+\frac{6}{7})(b−\frac{6}{7})$

Відповідь

$b^2−\frac{36}{49}$

Вправа 25

$(5k+6)(5k−6)$

Вправа 26

$(8j+4)(8j−4)$

Відповідь

$64j^2−16$

Вправа 27

$(11k+4)(11k−4)$

Вправа 28

$(9c+5)(9c−5)$

Відповідь

$81c^2−25$

Вправа 29

$(11−b)(11+b)$

Вправа 30

$(13−q)(13+q)$

Відповідь

$169−q^2$

Вправа 31

$(5−3x)(5+3x)$

Вправа 32

$(4−6y)(4+6y)$

Відповідь

$16−36y^2$

Вправа 33

$(9c−2d)(9c+2d)$

Вправа 34

$(7w+10x)(7w−10x)$

Відповідь

$49w^2−100x^2$

Вправа 35

$(m+\frac{2}{3}n)(m−\frac{2}{3}n)$

Вправа 36

$(p+\frac{4}{5}q)(p−\frac{4}{5}q)$

Відповідь

$p^2−\frac{16}{25}q^2$

Вправа 37

$(ab−4)(ab+4)$

Вправа 38

$(xy−9)(xy+9)$

Відповідь

$x^{2}y^2−81$

Вправа 39

$(uv−\frac{3}{5})(uv+\frac{3}{5})$

Вправа 40

$(rs−\frac{2}{7})(rs+\frac{2}{7})$

Відповідь

$r^{2}s^2−\frac{4}{49}$

Вправа 41

$(2x^2−3y^4)(2x^2+3y^4)$

Вправа 42

$(6m^3−4n^5)(6m^3+4n^5)$

Відповідь

$36m^6−16n^{10}$

Вправа 43

$(12p^3−11q^2)(12p^3+11q^2)$

Вправа 44

$(15m^2−8n^4)(15m^2+8n^4)$

Відповідь

$225m^4−64n^8$

Розпізнавання та використання відповідного спеціального зразка продукту

У наступних вправах знайдіть кожен продукт.

Вправа 45

а.$(p−3)(p+3)$

б.$(t−9)^2$

c.$(m+n)^2$

д.$(2x+y)(x−2y)$

Вправа 46

а.$(2r+12)^2$

б.$(3p+8)(3p−8)$

c.$(7a+b)(a−7b)$

д.$(k−6)^2$

Відповідь

а.$4r^2+48r+144$

б.$9p^2−64$

c.$7a^2−48ab−7b^2$

д.$k^2−12k+36$

Вправа 47

а.$(a^5−7b)^2$

б.$(x^2+8y)(8x−y^2)$

c.$(r^6+s^6)(r^6−s^6)$

д.$(y^4+2z)^2$

Вправа 48

а.$(x^5+y^5)(x^5−y^5)$

б.$(m^3−8n)^2$

c.$(9p+8q)^2$

д.$(r^2−s^3)(r^3+s^2)$

Відповідь

а.$x^{10}−y^{10}$

б. в.$m^6−16m^{3}n+64n^2$

$81p^2+144pq+64q^2$

д.$r^5+r^{2}s^2−r^{3}s^3−s^5$

Щоденна математика

Вправа 49

Психічна математика Ви можете використовувати добуток шаблону кон'югатів для множення чисел без калькулятора. Скажімо, потрібно помножити 47 разів 53. Подумайте про 47 як 50−3, а 53 як 50+3

1. Помножте (50−3) (50+3), використовуючи добуток візерунка сполучень,$(a−b)(a+b)=a^2−b^2$
2. Помножте 47·53 без використання калькулятора.
3. Який шлях вам легше? Чому?

Вправа 50

Психічна математика Ви можете використовувати шаблон біноміальних квадратів для множення чисел без калькулятора. Скажімо, потрібно квадрат 65. Подумайте про 65 як 60+5.

1. $(60+5)^2$Помножте за допомогою візерунка біноміальних квадратів,$(a+b)^2=a^2+2ab+b^2$
2. Квадрат 65 без використання калькулятора.
3. Який шлях вам легше? Чому?

Відповідь

1. 4 225
2. 4 225
3. Відповіді будуть відрізнятися.

Письмові вправи

Вправа 51

Як ви вирішуєте, який візерунок використовувати?

Вправа 52

Чому$(a+b)^2$ призводить до триноміалу, але (a−b) (a+b) призводить до біноміалу?

Відповідь

Відповіді будуть відрізнятися.

Вправа 53

Марта виконала наступну роботу над домашнім роботом:

$$\begin{array}{c} {(3−y)^2}\\ {3^2−y^2}\\ {9−y^2}\\ \nonumber \end{array}$$

Поясніть, що не так з роботою Марти.

Вправа 54

Скористайтеся порядком операцій, щоб показати, що$(3+5)^2$ це 64, а потім використайте цей числовий приклад, щоб пояснити, чому$(a+b)^2 \ne a^2+b^2$

Відповідь

Відповіді будуть відрізнятися.

Самостійна перевірка

ⓐ Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

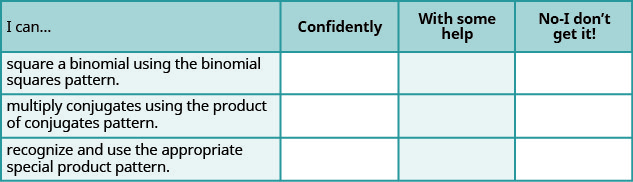
ⓑ За шкалою 1-10, як би ви оцінили своє володіння цим розділом у світлі ваших відповідей на контрольний список? Як ви можете це покращити?