Skip to main content
LibreTexts - Ukrayinska

6.4: Спеціальні продукти

  1. Last updated
  2. Save as PDF
  • Page ID
    59006

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Квадратний двочлен за допомогою візерунка біноміальних квадратів
    • Множення кон'югатів за допомогою візерунка добутку кон'югатів
    • Розпізнайте та використовуйте відповідний спеціальний візерунок продукту
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    Спрощення: а.\(9^2\) б.\((−9)^2\) с\(−9^2\).

    Якщо ви пропустили цю проблему, перегляньте Вправа 1.5.13.

    Квадрат біном з використанням візерунка біноміальних квадратів

    Математики люблять шукати закономірності, які полегшать їх роботу. Хорошим прикладом цього є квадратні двочлени. Хоча ви завжди можете отримати продукт, написавши біном двічі і використовуючи методи останнього розділу, менше роботи, якщо ви навчитеся використовувати візерунок.

    \[\begin{array}{ll}{\text { Let's start by looking at }(x+9)^{2} \text { . }}& \\ {\text { What does this mean? }} &{(x+9)^{2}} \\ {\text { It means to multiply }(x+9) \text { by itself. }} & {(x+9)(x+9)}\\ {\text { Then, using FOIL, we get: }} & {x^{2}+9 x+9 x+81}\\ {\text { Combining like terms gives: }} &{x^{2}+18 x+81} \\ \\ {\text { Here's another one: }} & {(y-7)^{2}} \\ {\text { Multiply }(y-7) \text { by itself. }} & {(y-7)(y-7)} \\ {\text { Using FOIL, we get: }} & {y^{2}-7 y-7 y+49} \\ {\text { And combining like terms: }} & {y^{2}-14 y+49} \\ \\ {\text { And one more: }} & {(2 x+3)^{2}} \\ {\text { Multiply. }} & {(2 x+3)(2 x+3)} \\ {\text { Use FOIL: }} & {\text { 4x }+6 x+6 x+9} \\ {\text { Combine like terms. }} & {4 x^{2}+12 x+9}\end{array} \nonumber\]

    Подивіться на ці результати. Ви бачите якісь візерунки?

    А як щодо кількості термінів? У кожному прикладі ми склали біноміал, і результат був триноміальним.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Тепер подивіться на перший термін в кожному результаті. Звідки воно взялося?

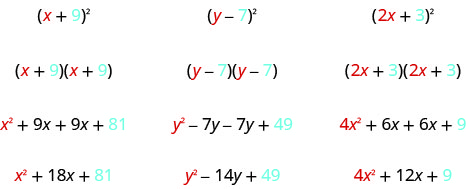
    Ця цифра має три стовпчики. Перший стовпець містить вираз x плюс 9, у дужках, у квадраті. Нижче це твір х плюс 9 і х плюс 9. Нижче це х квадрат плюс 9x плюс 9x плюс 81. Нижче це х квадрат плюс 18x плюс 81. Другий стовпець містить вираз y мінус 7, в дужках, в квадраті. Нижче цього добуток y мінус 7 і y мінус 7. Нижче це y в квадраті мінус 7y мінус 7y плюс 49. Нижче це вираз y в квадраті мінус 14y плюс 49. Третій стовпець містить вираз 2x плюс 3, в дужках, у квадраті. Нижче це продукт 2x плюс 3 і 2x плюс 3. Нижче це 4x квадрат плюс 6x плюс 6x плюс 9. Нижче це 4x квадрат плюс 12x плюс 9.

    Перший термін - це добуток перших членів кожного біноміала. Оскільки біноміали ідентичні, це просто квадрат першого члена!

    \[(a+b)^{2}=a^{2}+\underline{\qquad}+\underline{\qquad}\nonumber \]

    Щоб отримати перший термін виробу, квадратний перший член.

    Звідки взявся останній термін? Подивіться приклади і знайдіть викрійку.

    Останній термін - добуток останніх термінів, який є квадратом останнього члена.

    \[(a+b)^{2}=\underline{\qquad}+\underline{\qquad}+b^{2}\nonumber \]

    Щоб отримати останній термін виробу, квадратний останній термін.

    Нарешті, подивіться на середній термін. Зверніть увагу, що це сталося з додавання «зовнішнього» та «внутрішнього» термінів - які однакові! Таким чином, середній термін є подвійним добутком двох членів біноміального.

    \[(a+b)^{2}=\underline{\qquad}+2ab+\underline{\qquad}\nonumber \]

    \[(a+b)^{2}=\underline{\qquad}-2ab+\underline{\qquad}\nonumber \]

    Щоб отримати середній термін добутку, помножте добуток і подвоюйте їх добуток.

    Збираємо все разом:

    Біноміальний квадратний візерунок

    Якщо\(a\) і\(b\) є дійсними числами, то біноміальний квадратний візерунок

    \[\underbrace{(a+b)^{2}}_{(\text{binomial})^2} = \underbrace{a^{2}}_{(\text{first term})^2}  +  \underbrace{2 a b}_{2 \times (\text{product of terms})} + \underbrace{a^{2}}_{(\text{last term})^2} \nonumber\]

    Застосовуючи це до двох біноміальних типів:

    \[\begin{align*} (a+b)^{2} &= a^{2}+2 a b+b^{2} \\[4pt] (a-b)^{2} &=a^{2}- 2 a b + b^{2} \end{align*}\]

    Для квадратного двочлена:

    1. квадрат перший член
    2. квадрат останній термін
    3. подвоїти свій продукт

    Приклад чисел допомагає перевірити візерунок.

    \(\begin{array}{ll} & {(10+4)^{2}} \\{\text { Square the first term. }}& {10^{2}+\underline{\qquad}+\underline{\qquad}} \\ {\text { Square the last term. }} & {10^{2}+\underline{\qquad}+\frac{1}{4^{2}}} \\ {\text { Double their product. }} & {10^{2}+2 \cdot 10 \cdot 4+4^{2}} \\ {\text { Simplify. }} & {100+80+16} \\ {\text { Simplify. }} & {196}\end{array}\)

    Для множення\((10+4)^2\) зазвичай слід дотримуватися Порядку операцій.

    \[\begin{array}{c}{(10+4)^{2}} \\ {(14)^{2}} \\ {196}\end{array}\nonumber \]

    Візерунок працює!

    Приклад\(\PageIndex{1}\)

    \(\text { Multiply: }(x+5)^{2}\)

    Рішення:

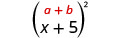      x плюс 5, в дужках, в квадраті. Над виразом знаходиться загальна формула a плюс b, в дужках, в квадраті.
    Квадратний перший член. х в квадраті плюс порожній плюс порожній. Над виразом знаходиться загальна форма a в квадраті плюс 2 a b плюс b в квадраті.
    Квадратний останній термін. х в квадраті плюс порожній плюс 5 в квадраті.
    Подвоїти виріб. х в квадраті плюс 2 рази х разів 5 плюс 5 в квадраті. Над цим виразом знаходиться загальна формула a в квадраті плюс 2 рази на b плюс b в квадраті.
    Спростити. \(x^{2}+10 x+25\)
    Спробуйте! \(\PageIndex{1}\)

    Помножити:\((x+9)^{2}\)

    Відповідь

    \(x^{2}+18 x+81\)

    Спробуйте! \(\PageIndex{2}\)

    Помножити:\((y+11)^{2}\)

    Відповідь

    \(y^{2}+22 y+121\)

    Приклад\(\PageIndex{2}\)

    Помножити:\((y-3)^{2}\)

    Рішення:

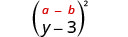      y мінус 3, в дужках, в квадраті. Над виразом знаходиться загальна формула a мінус b, в дужках, в квадраті.
    Квадратний перший член. Y в квадраті мінус порожній плюс порожній. Над виразом знаходиться загальна форма a в квадраті плюс 2 a b плюс b в квадраті.
    Квадратний останній термін. y в квадраті мінус порожній плюс 3 в квадраті.
    Подвоїти виріб. 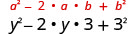Y в квадраті мінус y раз у раз 3 плюс 3 в квадраті. Над цим виразом знаходиться загальна формула a в квадраті плюс 2 рази на b плюс b в квадраті.
    Спростити. \(y^{2}-6 y+9\)
    Спробуйте! \(\PageIndex{3}\)

    Помножити:\((x-9)^{2}\)

    Відповідь

    \(x^{2}-18 x+81\)

    Спробуйте! \(\PageIndex{4}\)

    Помножити:\((p-13)^{2}\)

    Відповідь

    \(p^{2}-26 p+169\)

    Приклад\(\PageIndex{3}\)

    Помножити:\((4 x+6)^{2}\)

    Рішення:

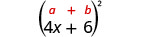      4 х плюс 6, в дужках, в квадраті. Над виразом знаходиться загальна формула a плюс b, в дужках, в квадраті.
    Використовуйте викрійку. 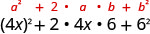4 х в квадраті плюс 2 рази 4 х рази 6 плюс 6 в квадраті. Над цим виразом знаходиться загальна формула a в квадраті плюс 2 рази на b плюс b в квадраті.
    Спростити. \(16 x^{2}+48 x+36\)
    Спробуйте! \(\PageIndex{5}\)

    Помножити:\((6 x+3)^{2}\)

    Відповідь

    \(36 x^{2}+36 x+9\)

    Спробуйте! \(\PageIndex{6}\)

    Помножити:\((4 x+9)^{2}\)

    Відповідь

    \(16 x^{2}+72 x+81\)

    Приклад\(\PageIndex{4}\)

    Помножити:\((2 x-3 y)^{2}\)

    Рішення:

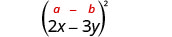      містить 2 x мінус 3 y, в дужках, у квадраті. Над виразом знаходиться загальна формула a плюс b, в дужках, в квадраті.
    Використовуйте викрійку. 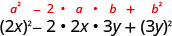2 х в квадраті мінус 2 рази 2 х рази 3 y плюс 3 у квадраті. Над цим виразом знаходиться загальна формула a в квадраті мінус 2 рази на b плюс b в квадраті.
    Спростити. \(4 x^{2}-12 x y+9 y^{2}\)
    Спробуйте! \(\PageIndex{7}\)

    Помножити:\((2 c-d)^{2}\)

    Відповідь

    \(4 c^{2}-4 c d+d^{2}\)

    Спробуйте! \(\PageIndex{8}\)

    Помножити:\((4 x-5 y)^{2}\)

    Відповідь

    \(16 x^{2}-40 x y+25 y^{2}\)

    Приклад\(\PageIndex{5}\)

    Помножити:\(\left(4 u^{3}+1\right)^{2}\)

    Рішення:

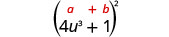      4 у кубі плюс 1, в дужках, в квадраті. Над виразом знаходиться загальна формула a плюс b, в дужках, в квадраті.
    Використовуйте викрійку. 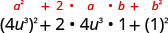4 у кубі, в дужках, в квадраті, плюс 2 рази 4 u куб раз 1 плюс 1 квадрат. Над цим виразом знаходиться загальна формула a в квадраті плюс 2 рази на b плюс b в квадраті.
    Спростити. \(16 u^{6}+8 u^{3}+1\)
    Спробуйте! \(\PageIndex{9}\)

    Помножити:\(\left(2 x^{2}+1\right)^{2}\)

    Відповідь

    \(4 x^{4}+4 x^{2}+1\)

    Спробуйте! \(\PageIndex{10}\)

    Помножити:\(\left(3 y^{3}+2\right)^{2}\)

    Відповідь

    \(9 y^{6}+12 y^{3}+4\)

    Множення кон'югатів за допомогою добутку візерунка кон'югатів

    Ми щойно побачили шаблон для квадратування бічленів, який ми можемо використовувати, щоб полегшити множення деяких біноміалів. Аналогічно існує візерунок і для іншого твору біноміалів. Але перш ніж ми перейдемо до цього, нам потрібно ввести певний словниковий запас.

    Що ви помічаєте про ці пари біноміалів?

    \[(x-9)(x+9) \qquad(y-8)(y+8)\qquad (2x-5)(2x+5) \nonumber\]

    Подивіться на перший член кожного біноміала в кожній парі.

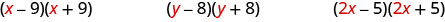
    Ця цифра має три вироби. Перший - х мінус 9, в дужках, раз х плюс 9, в дужках. Другий - у мінус 8, в дужках раз у плюс 8, в дужках. Останній - 2x мінус 5, в дужках, раз 2x плюс 5, в дужках

    Зверніть увагу, що перші терміни однакові в кожній парі.

    Подивіться на останні терміни кожного біноміала в кожній парі.

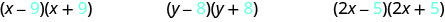
    Ця цифра має три вироби. Перший - х мінус 9, в дужках, раз х плюс 9, в дужках. Другий - у мінус 8, в дужках раз у плюс 8, в дужках. Останній - 2x мінус 5, в дужках, раз 2x плюс 5, в дужках.

    Зверніть увагу, що останні терміни однакові в кожній парі.

    Зверніть увагу, як кожна пара має одну суму і одну різницю.

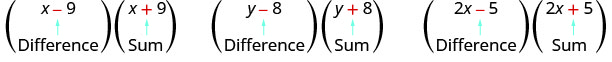
    Ця цифра має три вироби. Перший - х мінус 9, в дужках, раз х плюс 9, в дужках. Нижче х мінус 9 знаходиться слово «різниця». Нижче х плюс 9 знаходиться слово «сума». Другий - у мінус 8, в дужках раз у плюс 8, в дужках. Нижче у мінус 8 знаходиться слово «різниця». Нижче y плюс 8 - слово «сума». Останній - 2x мінус 5, в дужках, раз 2x плюс 5, в дужках. Нижче 2x мінус 5 - слово «різниця», а нижче 2x плюс 5 - слово «сума».

    Пара біноміалів, кожен з яких має однаковий перший член і той самий останній член, але один - сума, а один - різниця, має спеціальну назву. Вона називається сполученою парою і має вигляд (a−b), (a+b).

    Визначення: Сполучених пар

    Спряжена пара - це два двочлени виду

    \[(a-b),(a+b)\nonumber \]

    Пара біноміалів має один і той же перший член і той самий останній член, але один біноміал - це сума, а інший - різниця.

    Існує приємний візерунок для знаходження твору кон'югатів. Ви могли б, звичайно, просто ФОЛЬГА, щоб отримати продукт, але використання візерунка полегшує вашу роботу.

    Давайте подивимося на візерунок, використовуючи FOIL для множення деяких сполучених пар.

    \[\begin{array}{cc}{(x-9)(x+9)} & {(y-8)(y+8)} & (2x-5)(2x+5)\\ {x^{2}+9 x-9 x-81} & {y^{2}+8 y-8 y-64} & {4 x^{2}+10 x-10 x-25} \\ {x^{2}-81} & {y^{2}-64} & {4 x^{2}-25}\end{array}\nonumber \]

    Кожен перший член є добутком перших членів біноміалів, а оскільки вони ідентичні, це квадрат першого члена.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-}\underline{\qquad} \\ {\text { To get the}\textbf{ first term, square the first term. }}\end{array}\nonumber \]

    Останній термін прийшов з множення останніх членів, квадрата останнього члена.

    \[\begin{array}{c}{(a+b)(a-b)=a^{2}-b^{2}} \\ {\text { To get the}\textbf{ last term, square the last term. }}\end{array}\nonumber \]

    Що ви спостерігаєте щодо продуктів?

    Добуток двох біноміалів також є біноміальним! Більшість продуктів, отриманих з ФОЛЬГИ, були тріноміалами.

    Чому немає середнього терміну? Зверніть увагу на два середні члени, які ви отримуєте від FOIL об'єднати до 0 у кожному випадку, результат одного додавання та одного віднімання.

    Твір кон'югатів завжди має форму\(a^2-b^2\). Це називається різницею квадратів.

    Це призводить до закономірності:

    ВИРІБ З КОН'ЮГАТІВ ВІЗЕРУНКОМ

    Якщо\(a\) і\(b\) є дійсними числами,

    Ця цифра розділена на дві сторони. З лівого боку розташована наступна формула: добуток мінус b і a плюс b дорівнює квадрату мінус b в квадраті. З правого боку знаходиться та сама формула, позначена: мінус b і a плюс b позначені «сполученими», квадрат a і b в квадраті позначені квадратами, а знак мінус між квадратами позначається «різниця». Тому добуток двох спряжених називається різницею квадратів.

    Твір називається різницею квадратів.

    Щоб помножити сполучені, квадрат перший член, квадрат останній член, а твір запишіть як різницю квадратів.

    Давайте перевіримо цей шаблон на числовому прикладі.

    \(\begin{array}{ll} & (10-2)(10+2)\\ {\text { It is the product of conjugates, so the result will be the }} \\ {\text { difference of two squares. }} & \underline{\qquad} - \underline{\qquad}\\ {\text { Square the first term. }}& 10^2 - \underline{\qquad} \\ {\text { Square the last term. }} & 10^2 - 2^2\\ {\text { Simplify. }} & 100 -4\\ {\text { Simplify. }} & 96\\ {\text { What do you get using the Order of Operations? }} \\ \\ & (10-2)(10+2) \\ & (8)(12) \\ & 96 \end{array}\)

    Зверніть увагу, результат той же!

    Приклад\(\PageIndex{6}\)

    Помножити:\((x-8)(x+8)\)

    Рішення:

    По-перше, визнайте це як твір кон'югатів. Біноміали мають однакові перші члени, і ті ж останні члени, і один біноміал - це сума, а інший - різниця.

    Він підходить по викрійці. 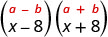Твір х мінус 8 і х плюс 8. Вище це загальна форма a мінус b, в дужках раз на плюс b, в дужках.
    Квадрат першого члена, x. 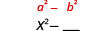x в квадраті мінус порожній. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Квадрат останнього члена, 8. 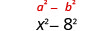х в квадраті мінус 8 в квадраті.
    Твір являє собою різницю квадратів. 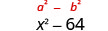х в квадраті мінус 64.
    Спробуйте! \(\PageIndex{11}\)

    Помножити:\((x-5)(x+5)\)

    Відповідь

    \(x^{2}-25\)

    Спробуйте! \(\PageIndex{12}\)

    Помножити:\((w-3)(w+3)\)

    Відповідь

    \(w^{2}-9\)

    Приклад\(\PageIndex{7}\)

    Помножити:\((2 x+5)(2 x-5)\)

    Рішення:

    Чи є біноміали кон'югати?

    Це твір кон'югатів. 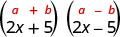Твір 2х плюс 5 і 2х мінус 5. Вище це загальна форма a мінус b, в дужках раз на плюс b, в дужках.
    Квадрат першого члена, 2 х. 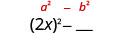2 х квадрат мінус порожній. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Квадрат останнього члена, 5. 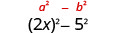2 х в квадраті мінус 5 в квадраті.
    Спростити. Твір являє собою різницю квадратів. 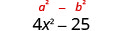4 х в квадраті мінус 25.
    Спробуйте! \(\PageIndex{13}\)

    Помножити:\((6 x+5)(6 x-5)\)

    Відповідь

    \(36 x^{2}-25\)

    Спробуйте! \(\PageIndex{14}\)

    Помножити:\((2 x+7)(2 x-7)\)

    Відповідь

    \(4 x^{2}-49\)

    Біноми в наступному прикладі можуть дивитися назад — змінна знаходиться у другому семестрі. Але два біноміали все ще є сполученими, тому ми використовуємо один і той же візерунок для їх множення.

    Приклад\(\PageIndex{8}\)

    Знайдіть товар:\((3+5 x)(3-5 x)\)

    Рішення:

    Це твір кон'югатів. 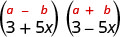Твір 3 плюс 5 х і 3 мінус 5 х Вище це загальна форма a плюс b, в дужках раз на мінус b, в дужках.
    Використовуйте викрійку. 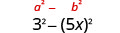3 в квадраті мінус 5 х в квадраті. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Спростити. \(9-25 x^{2}\)
    Спробуйте! \(\PageIndex{15}\)

    Помножити:\((7+4 x)(7-4 x)\)

    Відповідь

    \(49-16 x^{2}\)

    Спробуйте! \(\PageIndex{16}\)

    Помножити:\((9-2 y)(9+2 y)\)

    Відповідь

    \(81-4 y^{2}\)

    Тепер ми помножимо кон'югати, які мають дві змінні.

    Приклад\(\PageIndex{9}\)

    Знайдіть товар:\((5 m-9 n)(5 m+9 n)\)

    Рішення:

    Це підходить до викрійки. 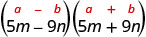5 м мінус 9 п і 5 м плюс 9 п Вище це загальна форма a плюс b, в дужках раз на мінус b, в дужках.
    Використовуйте викрійку. 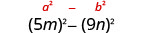5 м в квадраті мінус 9 п в квадраті. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Спростити. \(25 m^{2}-81 n^{2}\)
    Спробуйте! \(\PageIndex{17}\)

    Знайдіть товар:\((4 p-7 q)(4 p+7 q)\)

    Відповідь

    \(16 p^{2}-49 q^{2}\)

    Спробуйте! \(\PageIndex{18}\)

    Знайдіть товар:\((3 x-y)(3 x+y)\)

    Відповідь

    \(9 x^{2}-y^{2}\)

    Приклад\(\PageIndex{10}\)

    Знайдіть товар:\((c d-8)(c d+8)\)

    Рішення:

    Це підходить до викрійки. 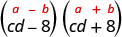Твір c d мінус 8 і c d плюс 8. Вище це загальна форма a плюс b, в дужках, раз на мінус b, в дужках.
    Використовуйте викрійку. 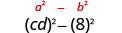c d в квадраті мінус 8 в квадраті. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Спростити. \(c^{2} d^{2}-64\)
    Спробуйте! \(\PageIndex{19}\)

    Знайдіть товар:\((x y-6)(x y+6)\)

    Відповідь

    \(x^{2} y^{2}-36\)

    Спробуйте! \(\PageIndex{20}\)

    Знайдіть товар:\((a b-9)(a b+9)\)

    Відповідь

    \(a^{2} b^{2}-81\)

    Приклад\(\PageIndex{11}\)

    Знайдіть товар:\(\left(6 u^{2}-11 v^{5}\right)\left(6 u^{2}+11 v^{5}\right)\)

    Рішення:

    Це підходить до викрійки. 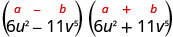Твір 6 u в квадраті мінус 11 v на п'яту потужність і 6 u в квадраті плюс 11 v на п'яту потужність. Вище це загальна форма a плюс b, в дужках, раз на мінус b, в дужках.
    Використовуйте викрійку. 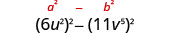6 u в квадраті, в дужках, квадрат, мінус 11 v до п'ятої потужності, в дужках, в квадраті. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Спростити. \(36 u^{4}-121 v^{10}\)
    Спробуйте! \(\PageIndex{21}\)

    Знайдіть товар:\(\left(3 x^{2}-4 y^{3}\right)\left(3 x^{2}+4 y^{3}\right)\)

    Відповідь

    \(9 x^{4}-16 y^{6}\)

    Спробуйте! \(\PageIndex{22}\)

    Знайдіть товар:\(\left(2 m^{2}-5 n^{3}\right)\left(2 m^{2}+5 n^{3}\right)\)

    Відповідь

    \(4 m^{4}-25 n^{6}\)

    Розпізнавання та використання відповідного спеціального зразка продукту

    Ми тільки що розробили спеціальні шаблони продуктів для біноміальних квадратів і для добутку кон'югатів. Вироби виглядають аналогічно, тому важливо визнати, коли доречно використовувати кожен з цих візерунків і помітити, чим вони відрізняються. Подивіться на дві моделі разом і зверніть увагу на їх подібності та відмінності.

    ПОРІВНЯННЯ СПЕЦІАЛЬНИХ МОДЕЛЕЙ ТОВАРУ

    \(\begin{array}{ll }{\textbf { Binomial Squares }}&{\textbf { Product of Conjugates }} \\ {(a+b)^{2}=a^{2}+2 a b+b^{2}} & {(a-b)(a+b)=a^{2}-b^{2}} \\ {(a-b)^{2}=a^{2}+2 a b+b^{2}} \\ {\text { - Squaring a binomial }}& {\text { - Multiplying conjugates }} \\ {\text { - Product is a trinomial }} & {\text { - Product is a binomial }} \\ {\text { - Inner and outer terms with FOIL are the same. }} &{\text { - Inner and outer terms with FOIL are opposites. }} \\ {\text { - Middle term is double the product of the terms. }} &{\text { - There is no middle term. }} \end{array}\)

    Приклад\(\PageIndex{12}\)

    Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:

    1. \((2 x-3)(2 x+3)\)
    2. \((8 x-5)^{2}\)
    3. \((6 m+7)^{2}\)
    4. \((5 x-6)(6 x+5)\)

    Рішення:

    1. \((2x−3)(2x+3)\)Це кон'югати. Вони мають однакові перші числа, і ті ж останні числа, і один біноміал - це сума, а інший - різниця. Він підходить до виробу з кон'югатів візерунком.

    Це підходить до викрійки. 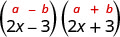Твір 2 х мінус 3 і 2 х плюс 3. Вище це загальна форма a плюс b, в дужках, раз на мінус b, в дужках.
    Використовуйте викрійку. 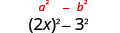2 х в квадраті мінус 3 в квадраті. Над цим є загальна форма a в квадраті мінус b в квадраті.
    Спростити. \(4 x^{2}-9\)

    2. \((8 x-5)^{2}\)Нас просять квадрат біном. Він підходить для візерунка біноміальних квадратів.

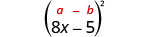      8 х мінус 5, в дужках, в квадраті. Над цим - загальна форма a мінус b, в дужках, в квадраті.
    Використовуйте викрійку. 8 х в квадраті мінус 2 рази 8 х разів 5 плюс 5 в квадраті. Над цим є загальна форма a в квадраті мінус 2 a b плюс b в квадраті.
    Спростити. \(64 x^{2}-80 x+25\)

    3. \((6 m+7)^{2}\)Знову ж таки, ми будемо квадратувати біном, тому ми використовуємо шаблон біноміальних квадратів.

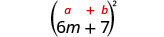      6 м плюс 7, в дужках, в квадраті. Над цим є загальна форма a плюс b, в дужках, в квадраті.
    Використовуйте викрійку. 6 м в квадраті плюс 2 рази 6 м раз 7 плюс 7 в квадраті. Вище це загальна форма a в квадраті плюс 2 a b плюс b в квадраті.
    Спростити. \(36 m^{2}+84 m+49\)

    4. \((5 x-6)(6 x+5)\)Цей виріб не підходить по викрійках, тому будемо використовувати фольгу.

    \(\begin{array}{ll} & (5 x-6)(6 x+5)\\ {\text { Use FOIL. }} & {30 x^{2}+25 x-36 x-30} \\ {\text { Simplify. }} & {30 x^{2}-11 x-30}\end{array}\)

    Спробуйте! \(\PageIndex{23}\)

    Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:

    1. \((9b−2)(2b+9)\)
    2. \((9p−4)2\)
    3. \((7y+1)^2\)
    4. \((4r-3)(4r+3)\)
    Відповідь
    1. ФОЛЬГА;\(18 b^{2}+77 b-18\)
    2. Біноміальні квадрати;\(81 p^{2}-72 p+16\)
    3. Біноміальні квадрати;\(49 y^{2}+14 y+1\)
    4. Твір кон'югатів;\(16 r^{2}-9\)
    Спробуйте! \(\PageIndex{24}\)

    Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:

    1. \((6x+7)^2\)
    2. \((3x−4)(3x+4)\)
    3. \((2x−5)(5x−2)\)
    4. \((6n−1)^2\)
    Відповідь
    1. Біноміальні квадрати;\(36 x^{2}+84 x+49\)
    2. Твір кон'югатів;\(9 x^{2}-16\)
    3. ФОЛЬГА;\(10 x^{2}-29 x+10\)
    4. Біноміальні квадрати;\(36 n^{2}-12 n+1\)
    Примітка

    Отримайте доступ до цих онлайн-ресурсів для додаткової інструкції та практики за допомогою спеціальних продуктів:

    • Спеціальні продукти

    Ключові концепції

    • Біноміальні квадрати візерунок
      • Якщо a, b - дійсні числа,
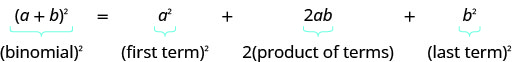
        Без тексту Alt
      • \((a+b)^{2}=a^{2}+2 a b+b^{2}\)
      • \((a-b)^{2}=a^{2}-2 a b+b^{2}\)
      • Для квадратного двочлена: квадрат першого члена, квадрат останнього члена, подвоїти їх добуток.
    • Продукт кон'югатів візерунок
      • Якщо a, ba, b є дійсними числами,
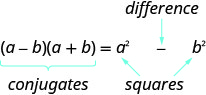
        Без тексту Alt
      • \((a-b)(a+b)=a^{2}-b^{2}\)
      • Твір називається різницею квадратів.
    • Для множення кон'югатів:
      • квадрат, перший член, квадрат, останній член, запишіть його як різницю квадратів.

    Глосарій

    сполучені пари
    Спряжена пара - це два біноміали форми\((a−b)\) і\((a+b)\); пара біноміалів кожен має однаковий перший член і той самий останній член, але один біноміал - це сума, а інший - різниця.