Глава 4 Огляд вправ

Глава 4 Огляд вправ

Прямокутна система координат

Графік точок у прямокутній системі координат

У наступних вправах розмістіть кожну точку в прямокутній системі координат.

Вправа$\PageIndex{1}$

1. (−1, −5)
2. (−3,4)
3. (2, −3)
4. $\left(1, \frac{5}{2}\right)$

Вправа$\PageIndex{2}$

1. (4,3)
2. (−4,3)
3. (−4, −3)
4. (4, −3)

Відповідь

Вправа$\PageIndex{3}$

1. (−2,0)
2. (0, −4)
3. (0,5)
4. (3,0)

Вправа$\PageIndex{4}$

1. $\left(2, \frac{3}{2}\right)$
2. $\left(3, \frac{4}{3}\right)$
3. $\left(\frac{1}{3},-4\right)$
4. $\left(\frac{1}{2},-5\right)$

Відповідь

Визначення точок на графіку

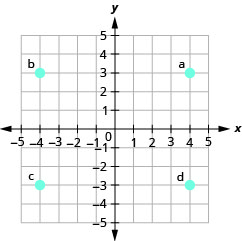
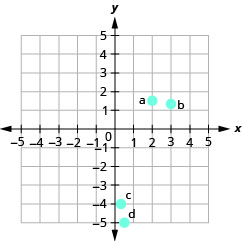
У наступних вправах назвіть впорядковану пару кожної точки, показаної в прямокутній системі координат.

Вправа$\PageIndex{5}$

Вправа$\PageIndex{6}$

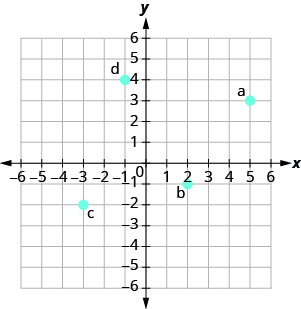
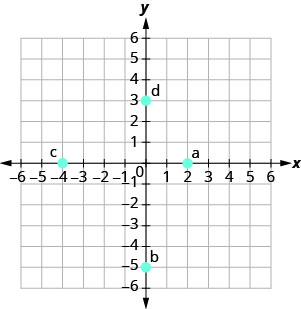
Відповідь

а. (2,0)

b (0, −5)

c (−4,0)

д (0,3)

Перевірка розв'язків рівняння у двох змінних

У наступних вправах, які впорядковані пари є розв'язками заданих рівнянь?

Вправа$\PageIndex{7}$

$5x+y=10$

1. (5,1)
2. (2,0)
3. (4, −10)

Вправа$\PageIndex{8}$

$y=6x−2$

1. (1,4)
2. $\left(\frac{1}{3}, 0\right)$
3. (6, −2)

Відповідь

1, 2

Заповніть таблицю розв'язків лінійного рівняння у двох змінних

У наступних вправах заповніть таблицю, щоб знайти рішення кожного лінійного рівняння.

Вправа$\PageIndex{9}$

$y=4 x-1$

х	у	(х, у)
0
1
-2

Вправа$\PageIndex{10}$

$y=-\frac{1}{2} x+3$

х	у	(х, у)
0
4
-2

Відповідь

х	у	(х, у)
0	3	(0,3)
4	1	(4, 1)
−2	4	(−2,4)

Вправа$\PageIndex{11}$

$x+2 y=5$

х	у	(х, у)
	0
1
-1

Вправа$\PageIndex{12}$

$3x+2y=6$

х	у	(х, у)
0
	0
-2

Відповідь

х	у	(х, у)
0	−3	(0, −3)
2	0	(2,0)
−2	−6	(−2, −6)

Пошук розв'язків лінійного рівняння у двох змінних

У наступних вправах знайдіть три рішення кожного лінійного рівняння.

Вправа$\PageIndex{13}$

$x+y=3$

Вправа$\PageIndex{14}$

$x+y=-4$

Відповідь

Відповіді будуть відрізнятися.

Вправа$\PageIndex{15}$

$y=3 x+1$

Вправа$\PageIndex{16}$

$y=-x-1$

Відповідь

Відповіді будуть відрізнятися.

Графічні лінійні рівняння

Визнати зв'язок між розв'язками рівняння та його графіком

У наступних вправах для кожної впорядкованої пари вирішуйте:

1. Чи є впорядкована пара розв'язком рівняння?
2. Чи є точка на лінії?

Вправа$\PageIndex{17}$

$y=−x+4$

(0,4) (−1,3)

(2,2) (−2,6)

Вправа$\PageIndex{18}$

$y=\frac{2}{3} x-1$
$(0,-1) (3,1)$
$(-3,-3) (6,4)$

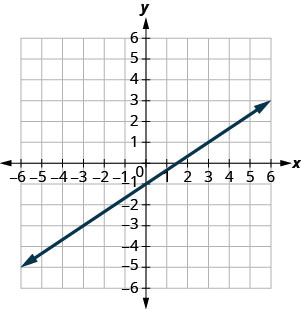
Відповідь

1. так; так
2. так; ні

Графік лінійного рівняння шляхом побудови точок

У наступних вправах граф за допомогою побудови точок.

Вправа$\PageIndex{19}$

$y=4x-3$

Вправа$\PageIndex{20}$

$y=-3x$

Відповідь

Вправа$\PageIndex{21}$

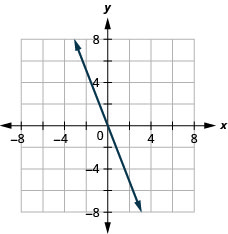
$y=\frac{1}{2} x+3$

Вправа$\PageIndex{22}$

$x-y=6$

Відповідь

Вправа$\PageIndex{23}$

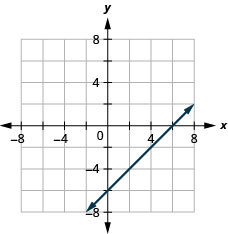
$2x+y=7$

Вправа$\PageIndex{24}$

$3x-2y=6$

Відповідь

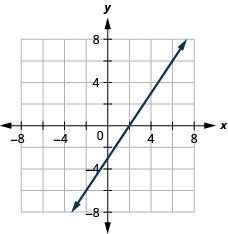
Графік Вертикальні та Горизонтальні лінії

У наступних вправах проведіть графік кожного рівняння.

Вправа$\PageIndex{25}$

$y=-2$

Вправа$\PageIndex{26}$

$x=3$

Відповідь

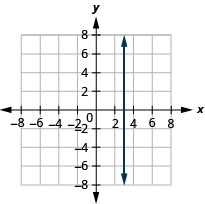
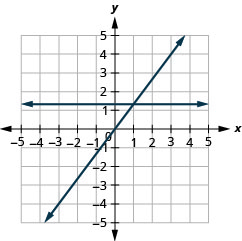
У наступних вправах графік кожної пари рівнянь в одній і тій же прямокутній системі координат.

Вправа$\PageIndex{27}$

$y=-2 x$і$y=-2$

Вправа$\PageIndex{28}$

$y=\frac{4}{3} x$і$y=\frac{4}{3}$

Відповідь

Графік з перехопленнями

Визначте$x$ - і$y$ -Перехоплення на графіку

У наступних вправах знайдіть$x$ - і$y$ -перехоплення.

Вправа$\PageIndex{29}$

Вправа$\PageIndex{30}$

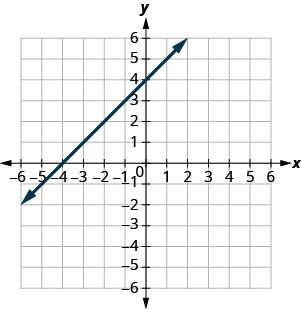
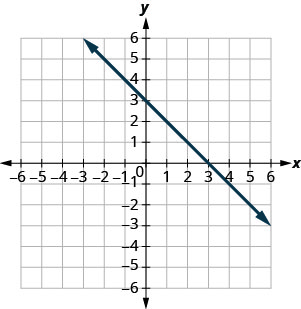
Відповідь

$(3,0)$і$(0,3)$

Знайти$x$ - і$y$ -перехоплення з рівняння прямої

У наступних вправах знайдіть перехоплення кожного рівняння.

Вправа$\PageIndex{31}$

$x+y=5$

Вправа$\PageIndex{32}$

$x-y=-1$

Відповідь

$(-1,0),(0,1)$

Вправа$\PageIndex{33}$

$x+2y=6$

Вправа$\PageIndex{34}$

$2x+3y=12$

Відповідь

$(6,0),(0,4)$

Вправа$\PageIndex{35}$

$y=\frac{3}{4} x-12$

Вправа$\PageIndex{36}$

$y=3x$

Відповідь

$(0,0)$

Графік лінії за допомогою перехоплення

У наступних вправах граф з використанням перехоплень.

Вправа$\PageIndex{37}$

$-x+3y=3$

Вправа$\PageIndex{38}$

$x+y=-2$

Відповідь

Вправа$\PageIndex{39}$

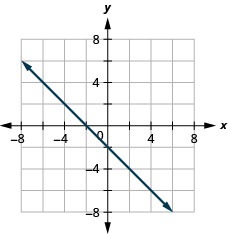
$x-y=4$

Вправа$\PageIndex{40}$

$2x-y=5$

Відповідь

Вправа$\PageIndex{41}$

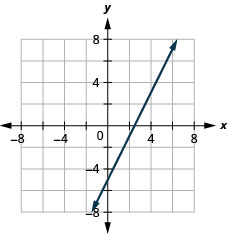
$2x-4y=8$

Вправа$\PageIndex{42}$

$y=2x$

Відповідь

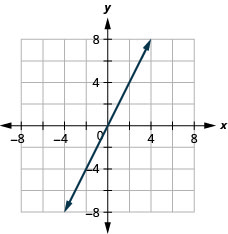
Нахил лінії

Використовуйте геоборди для моделювання схилу

У наступних вправах знайдіть нахил, змодельований на кожній геоборді.

Вправа$\PageIndex{43}$

Вправа$\PageIndex{44}$

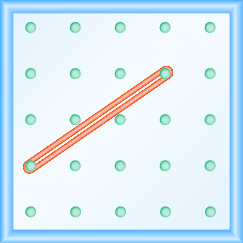
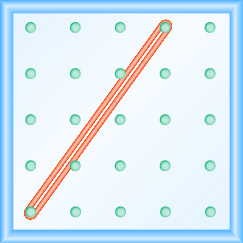
Відповідь

$\frac{4}{3}$

Вправа$\PageIndex{45}$

Вправа$\PageIndex{46}$

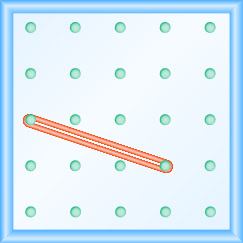
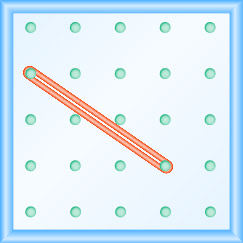
Відповідь

$-\frac{2}{3}$

Вправа$\PageIndex{47}$

$\frac{1}{3}$

Вправа$\PageIndex{48}$

$\frac{3}{2}$

Відповідь

Вправа$\PageIndex{49}$

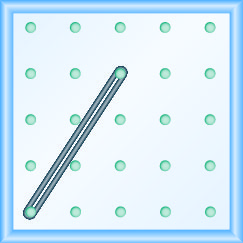
$-\frac{2}{3}$

Вправа$\PageIndex{50}$

$-\frac{1}{2}$

Відповідь

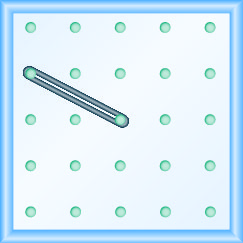
$m=\frac{\text { rise }}{\text { run }}$Використовується для пошуку нахилу лінії з її графіка

У наступних вправах знайдіть нахил кожної показаної лінії.

Вправа$\PageIndex{51}$

Вправа$\PageIndex{52}$

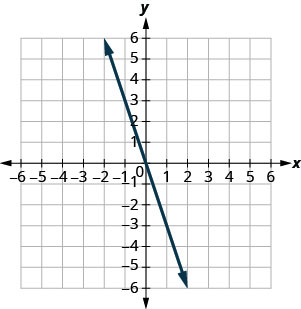
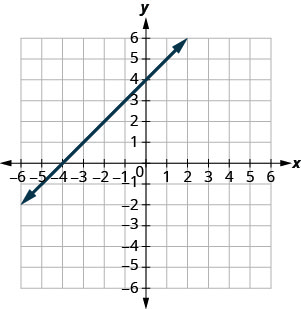
Відповідь

1

Вправа$\PageIndex{53}$

Вправа$\PageIndex{54}$

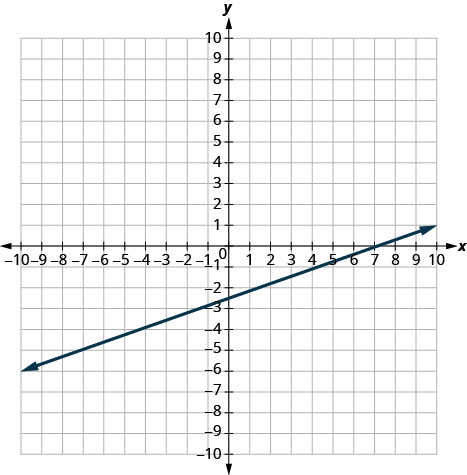
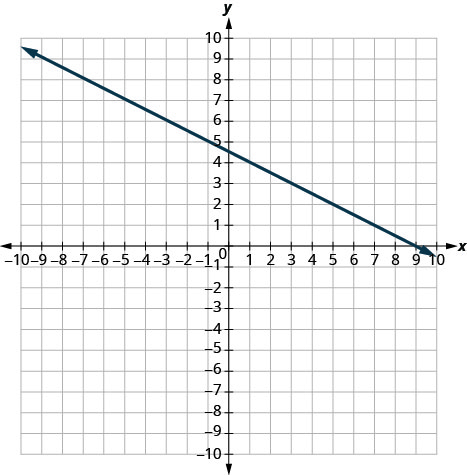
Відповідь

$-\frac{1}{2}$

Знайти нахил горизонтальних і вертикальних ліній

У наступних вправах знайдіть нахил кожної лінії.

Вправа$\PageIndex{55}$

$y=2$

Вправа$\PageIndex{56}$

$x=5$

Відповідь

невизначений

Вправа$\PageIndex{57}$

$x=-3$

Вправа$\PageIndex{58}$

$y=-1$

Відповідь

0

Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

У наступних вправах використовуйте формулу нахилу, щоб знайти нахил лінії між кожною парою точок.

Вправа$\PageIndex{59}$

$(-1,-1),(0,5)$

Вправа$\PageIndex{60}$

$(3,5),(4,-1)$

Відповідь

−6

Вправа$\PageIndex{61}$

$(-5,-2),(3,2)$

Вправа$\PageIndex{62}$

$(2,1),(4,6)$

Відповідь

$\frac{5}{2}$

Графік лінії з заданою точкою та нахилом

У наступних вправах графік кожної лінії з заданою точкою і нахилом.

Вправа$\PageIndex{63}$

$(2,-2) ; \quad m=\frac{5}{2}$

Вправа$\PageIndex{64}$

$(-3,4) ; \quad m=-\frac{1}{3}$

Відповідь

Вправа$\PageIndex{65}$

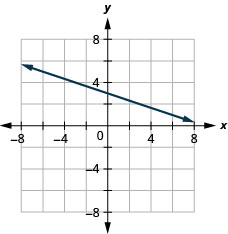
$x$-перехопити$-4 ; \quad m=3$

Вправа$\PageIndex{66}$

$y$-перехопити$1 ; \quad m=-\frac{3}{4}$

Відповідь

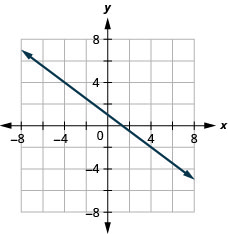
Вирішіть програми нахилу

У наступних вправах вирішуйте ці програми нахилу.

Вправа$\PageIndex{67}$

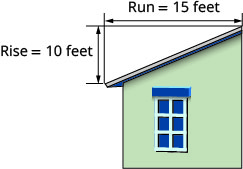
Дах, зображений нижче, має підйом$10$ ніг і пробіг$15$ ніг. Який її ухил?

Вправа$\PageIndex{68}$

Гірська дорога піднімається$50$ ногами для$500$ пробіжки. Який її ухил?

Відповідь

$\frac{1}{10}$

Форма перехоплення рівняння прямої

Розпізнати зв'язок між графом та формою нахилу—перехоплення рівняння прямої

У наступних вправах використовуйте графік, щоб знайти нахил і y -перехоплення кожної лінії. Порівняйте значення з рівнянням$y=mx+b$.

Вправа$\PageIndex{69}$

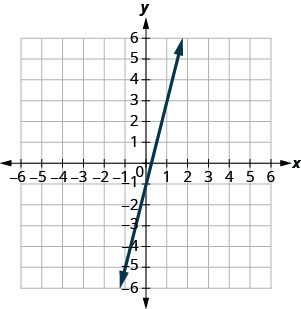
$y=4x−1$

Вправа$\PageIndex{70}$

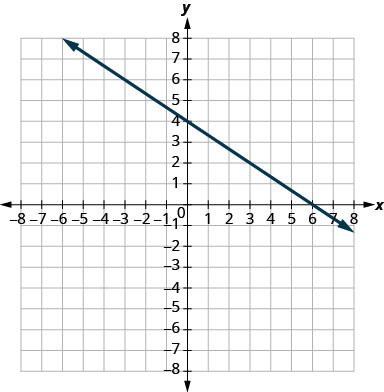
$y=-\frac{2}{3} x+4$

Відповідь

нахил$m=-\frac{2}{3}$ і$y$ -перехоплення$(0,4)$

Визначте нахил і Y-перехоплення з рівняння прямої

У наступних вправах визначте нахил і$y$ -перехоплення кожної лінії.

Вправа$\PageIndex{71}$

$y=-4 x+9$

Вправа$\PageIndex{72}$

$y=\frac{5}{3} x-6$

Відповідь

$\frac{5}{3} ;(0,-6)$

Вправа$\PageIndex{73}$

$5x+y=10$

Вправа$\PageIndex{74}$

$4x-5y=8$

Відповідь

$\frac{4}{5} ;\quad \left(0,-\frac{8}{5}\right)$

Графік лінії, використовуючи її нахил і перехоплення

У наступних вправах графік лінії кожного рівняння, використовуючи його нахил і$y$ -перехоплення.

Вправа$\PageIndex{75}$

$y=2x+3$

Вправа$\PageIndex{76}$

$y=-x-1$

Відповідь

Вправа$\PageIndex{77}$

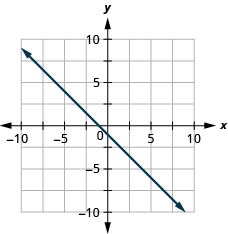
$y=-\frac{2}{5} x+3$

Вправа$\PageIndex{78}$

$4x-3y=12$

Відповідь

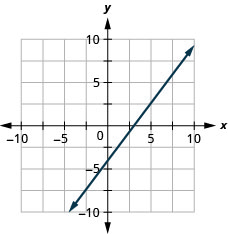
У наступних вправах визначте найбільш зручний метод графіка кожного рядка.

Вправа$\PageIndex{79}$

$x=5$

Вправа$\PageIndex{80}$

$y=-3$

Відповідь

горизонтальна лінія

Вправа$\PageIndex{81}$

$2x+y=5$

Вправа$\PageIndex{82}$

$x-y=2$

Відповідь

перехоплює

Вправа$\PageIndex{83}$

$y=x+2$

Вправа$\PageIndex{84}$

$y=\frac{3}{4} x-1$

Відповідь

побудова точок

Графік та інтерпретація застосувань перехоплення нахилу

Вправа$\PageIndex{85}$

Кетрін - приватний шеф-кухар. Рівняння$C=6.5m+42$ моделює співвідношення між її$C$ тижневою вартістю, у доларах та кількістю їжі$m$, яку вона обслуговує.

1. Знайдіть вартість Кетрін на тиждень, коли вона не подає їжі.
2. Знайти вартість за тиждень, коли вона подає$14$ страви.
3. Інтерпретувати нахил і$C$ -перехоплення рівняння.
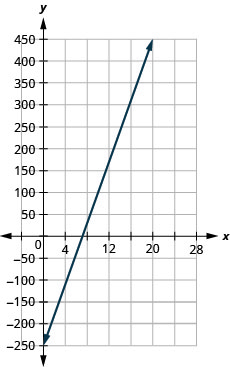
4. Графік рівняння.

Вправа$\PageIndex{86}$

Марджорі викладає фортепіано. Рівняння$P=35h−250$ моделює співвідношення між її тижневим прибутком$P$, у доларах та кількістю учнівських уроків$s$, які вона викладає.

1. Знайдіть прибуток Марджорі за тиждень, коли вона не викладає жодних учнів.
2. Знайдіть прибуток за тиждень, коли вона викладає$20$ студентські уроки.
3. Інтерпретувати нахил і$P$ -перехоплення рівняння.
4. Графік рівняння.

Відповідь

1. $−$250$
2. $$450$
3. Нахил$35$, означає, що щотижневий прибуток Марджорі$P$, збільшується$$35$ на кожен додатковий урок учня, який вона викладає. $P$-Перехоплення означає, що коли кількість уроків є$0$, Марджорі програє$$250$.

Використання нахилів для визначення паралельних ліній

У наступних вправах використовуйте нахили і$y$ -перехоплення, щоб визначити, чи паралельні лінії.

Вправа$\PageIndex{87}$

$4x-3y=-1 ; \quad y=\frac{4}{3} x-3$

Вправа$\PageIndex{88}$

$2 x-y=8 ; \quad x-2 y=4$

Відповідь

не паралельно

Використання нахилів для визначення перпендикулярних ліній

У наступних вправах використовуйте нахили і y-перехоплення, щоб визначити, чи є лінії перпендикулярними.

Вправа$\PageIndex{89}$

$y=5x-1 ; \quad 10x+2y=0$

Вправа$\PageIndex{90}$

$3x-2y=5 ; \quad 2x+3y=6$

Відповідь

перпендикулярний

Знайти рівняння прямої

Знайти рівняння прямої з заданим нахилом та y -перехопленням

У наступних вправах знайдіть рівняння прямої з заданим нахилом і$y$ -перехопленням. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{91}$

нахил$\frac{1}{3}$ і$y$ -перехоплення$(0,-6)$

Вправа$\PageIndex{92}$

нахил$-5$ і$y$ -перехоплення$(0,-3)$

Відповідь

$y=-5x-3$

Вправа$\PageIndex{93}$

нахил$0$ і$y$ -перехоплення$(0,4)$

Вправа$\PageIndex{94}$

нахил$-2$ і$y$ -перехоплення$(0,0)$

Відповідь

$y=-2x$

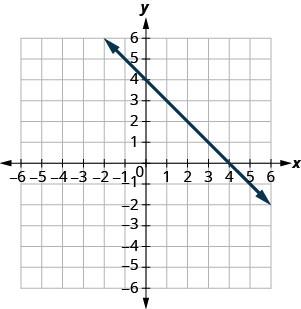
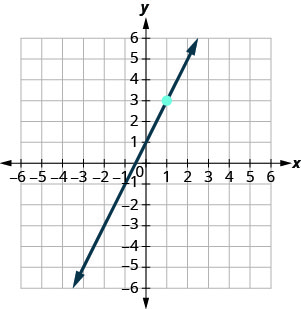
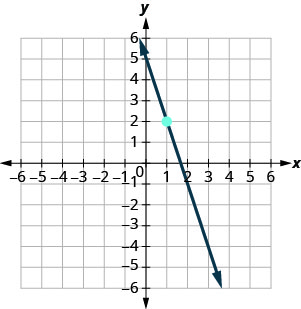
У наступних вправах знайдіть рівняння лінії, показане на кожному графіку. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{95}$

Вправа$\PageIndex{96}$

Відповідь

$y=-3x+5$

Вправа$\PageIndex{97}$

Вправа$\PageIndex{98}$

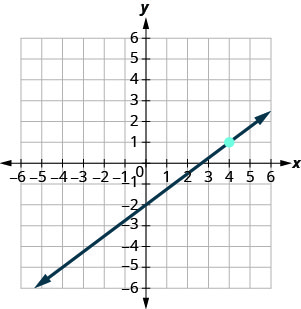
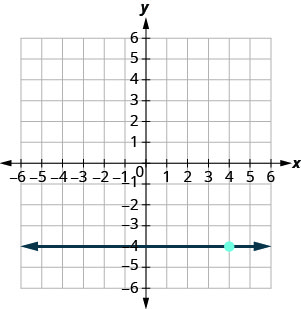
Відповідь

$y=-4$

Знайти рівняння прямої з заданим нахилом і точкою

У наступних вправах знайдіть рівняння прямої з заданим нахилом і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{99}$

$m=-\frac{1}{4},$точка$(-8,3)$

Вправа$\PageIndex{100}$

$m=\frac{3}{5},$точка$(10,6)$

Відповідь

$y=\frac{3}{5} x$

Вправа$\PageIndex{101}$

Горизонтальна лінія, що містить$(-2,7)$

Вправа$\PageIndex{102}$

$m=-2,$точка$(-1,-3)$

Відповідь

$y=-2x-5$

Знайти рівняння прямої за двома точками

У наступних вправах знайдіть рівняння рядка, що містить задані точки. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{103}$

$(2,10)$і$(-2,-2)$

Вправа$\PageIndex{104}$

$(7,1)$і$(5,0)$

Відповідь

$y=\frac{1}{2} x-\frac{5}{2}$

Вправа$\PageIndex{105}$

$(3,8)$і$(3,-4)$

Вправа$\PageIndex{106}$

$(5,2)$і$(-1,2)$

Відповідь

$y=2$

Знайти рівняння прямої, паралельної заданій прямій

У наступних вправах знайдіть рівняння прямої, паралельної заданій лінії і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{107}$

$y=-3x+6,$точка лінії$(1,-5)$

Вправа$\PageIndex{108}$

$2x+5y=-10,$точка лінії$(10,4)$

Відповідь

$y=-\frac{2}{5} x+8$

Вправа$\PageIndex{109}$

$x=4,$точка лінії$(-2,-1)$

Вправа$\PageIndex{110}$

$y=-5,$точка лінії$(-4,3)$

Відповідь

$y=3$

Знайти рівняння прямої, перпендикулярної заданій прямій

У наступних вправах знайдіть рівняння прямої, перпендикулярної заданій лінії і містить задану точку. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{111}$

$y=-\frac{4}{5} x+2,$точка лінії$(8,9)$

Вправа$\PageIndex{112}$

$2x-3y=9,$точка лінії$(-4,0)$

Відповідь

$y=-\frac{3}{2} x-6$

Вправа$\PageIndex{113}$

$y=3,$точка лінії$(-1,-3)$

Вправа$\PageIndex{114}$

$x=-5$точка лінії$(2,1)$

Відповідь

$y=1$

Лінійні нерівності графа

Перевірка рішень нерівності в двох змінних

У наступних вправах визначте, чи є кожна впорядкована пара розв'язком заданої нерівності.

Вправа$\PageIndex{115}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності$y<x−3$:

1. $(0,1)$
2. $(−2,−4)$
3. $(5,2)$
4. $(3,−1)$
5. $(−1,−5)$

Вправа$\PageIndex{116}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності$x+y>4$:

1. $(6,1)$
2. $(−3,6)$
3. $(3,2)$
4. $(−5,10)$
5. $(0,0)$

Відповідь

1. так
2. ні
3. так
4. так
5. ні

Визнати зв'язок між розв'язками нерівності та її графіком

У наступних вправах напишіть нерівність, показану затіненою областю.

Вправа$\PageIndex{117}$

Запишіть нерівність, показану графіком, з граничною лінією$y=−x+2$.

Вправа$\PageIndex{118}$

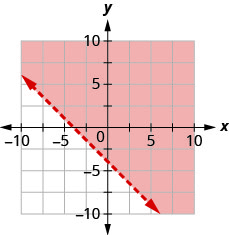
Запишіть нерівність, показану графіком, з граничною лінією$y=\frac{2}{3} x-3$

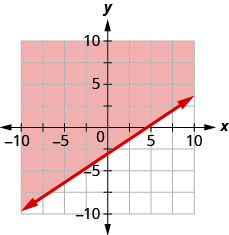
Відповідь

$y>\frac{2}{3} x-3$

Вправа$\PageIndex{119}$

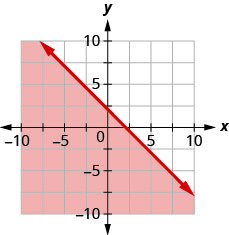
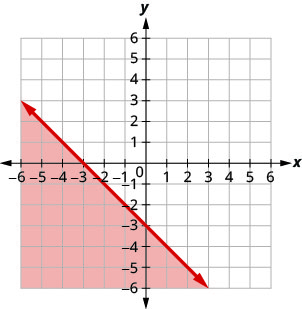
Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією$x+y=−4$.

Вправа$\PageIndex{120}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією$x−2y=6$.

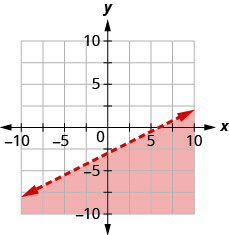
Відповідь

$x-2 y \geq 6$

Лінійні нерівності графа

У наступних вправах наведіть графік кожної лінійної нерівності.

Вправа$\PageIndex{121}$

Графік лінійної нерівності$y>\frac{2}{5} x-4$

Вправа$\PageIndex{122}$

Графік лінійної нерівності$y \leq-\frac{1}{4} x+3$

Відповідь

Вправа$\PageIndex{123}$

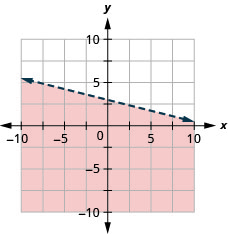
Графік лінійної нерівності$x-y \leq 5$

Вправа$\PageIndex{124}$

Графік лінійної нерівності$3 x+2 y>10$

Відповідь

Вправа$\PageIndex{125}$

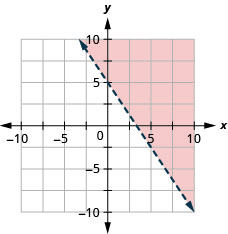
Графік лінійної нерівності$y \leq-3 x$

Вправа$\PageIndex{126}$

Графік лінійної нерівності$y<6$

Відповідь

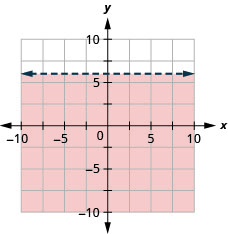
Практика Тест

Вправа$\PageIndex{1}$

Покладіть кожну точку в прямокутній системі координат.

1. $(2,5)$
2. $(−1,−3)$
3. $(0,2)$
4. $\left(-4, \frac{3}{2}\right)$
5. $(5,0)$

Вправа$\PageIndex{2}$

Які з заданих впорядкованих пар є розв'язками рівняння$3x−y=6$?

1. $(3,3)$
2. $(2,0)$
3. $(4,−6)$

Відповідь

1. так
2. так
3. ні

Вправа$\PageIndex{3}$

Знайти три розв'язки лінійного рівняння$y=-2x-4$

Вправа$\PageIndex{4}$

Знайти$x$ - і$y$ -перехоплення рівняння$4x-3y=12$

Відповідь

$(3,0),(0,-4)$

Знайдіть нахил кожної показаної лінії.

Вправа$\PageIndex{5}$

Вправа$\PageIndex{6}$

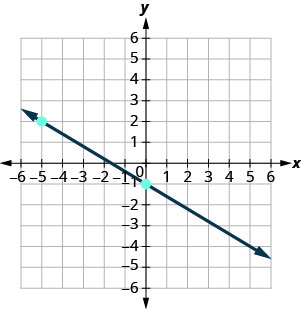
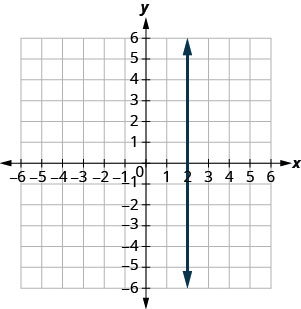
Відповідь

невизначений

Вправа$\PageIndex{7}$

Вправа$\PageIndex{8}$

Знайти нахил лінії між точками$(5,2)$ і$(-1,-4)$

Відповідь

1

Вправа$\PageIndex{9}$

Графік лінії з нахилом$\frac{1}{2}$, що містить точку$(-3,-4)$

Графік лінії для кожного з наступних рівнянь.

Вправа$\PageIndex{10}$

$y=\frac{5}{3} x-1$

Відповідь

Вправа$\PageIndex{11}$

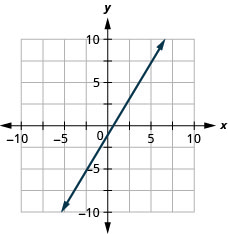
$y=-x$

Вправа$\PageIndex{12}$

$x-y=2$

Відповідь

Вправа$\PageIndex{13}$

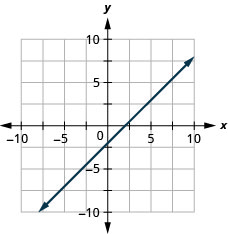
$4x+2y=-8$

Вправа$\PageIndex{14}$

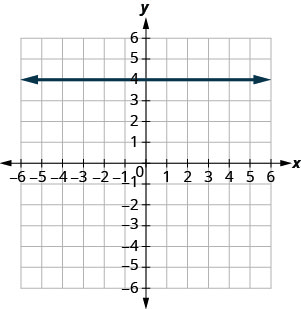
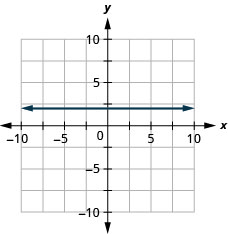
$y=2$

Відповідь

Вправа$\PageIndex{15}$

$x=-3$

Знайдіть рівняння кожного рядка. Запишіть рівняння у формі нахилу—перехоплення.

Вправа$\PageIndex{16}$

нахил$-\frac{3}{4}$ і$y$ -перехоплення$(0,-2)$

Відповідь

$y=-\frac{3}{4} x-2$

Вправа$\PageIndex{17}$

$m=2,$точка$(-3,-1)$

Вправа$\PageIndex{18}$

що містить$(10,1)$ і$(6,-1)$

Відповідь

$y=\frac{1}{2} x-4$

Вправа$\PageIndex{19}$

паралельно лінії,$y=-\frac{2}{3} x-1,$ що містить точку$(-3,8)$

Вправа$\PageIndex{20}$

перпендикулярно лінії$y=\frac{5}{4} x+2,$, що містить точку$(-10,3)$

Відповідь

$y=-\frac{4}{5} x-5$

Вправа$\PageIndex{21}$

Запишіть нерівність, показану графіком, з граничною лінією$y=−x−3$.

Графік кожної лінійної нерівності.

Вправа$\PageIndex{22}$

$y>\frac{3}{2} x+5$

Відповідь

Вправа$\PageIndex{23}$

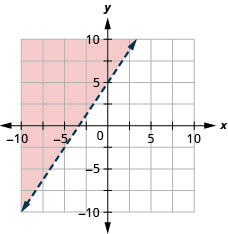
$x-y \geq-4$

Вправа$\PageIndex{24}$

$y \leq-5 x$

Відповідь

Вправа$\PageIndex{1}$

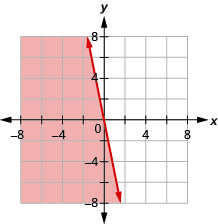
$y<3$