4.7E: Вправи

Last updated

Oct 27, 2022
Save as PDF
- 4.7: Графіки лінійних нерівностей
- Глава 4 Огляд вправ

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Практика робить досконалим

Перевірка рішень нерівності в двох змінних

У наступних вправах визначте, чи є кожна впорядкована пара розв'язком заданої нерівності.

Вправа $\PageIndex{1}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $y>x−1$ :

$(0,1)$
$(−4,−1)$
$(4,2)$
$(3,0)$
$(−2,−3)$

Вправа $\PageIndex{2}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $y>x−3$ :

$(0,0)$
$(2,1)$
$(−1,−5)$
$(−6,−3)$
$(1,0)$

Відповідь

так
ні
ні
так
ні

Вправа $\PageIndex{3}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $y<x+2$ :

$(0,3)$
$(−3,−2)$
$(−2,0)$
$(0,0)$
$(−1,4)$

Вправа $\PageIndex{4}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $y<x+5$ :

$(−3,0)$
$(1,6)$
$(−6,−2)$
$(0,1)$
$(5,−4)$

Відповідь

так
ні
ні
так
так

Вправа $\PageIndex{5}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $x+y>4$ :

$(5,1)$
$(−2,6)$
$(3,2)$
$(10,−5)$
$(0,0)$

Вправа $\PageIndex{6}$

Визначте, чи є кожна впорядкована пара розв'язком нерівності $x+y>2$ :

$(1,1)$
$(4,−3)$
$(0,0)$
$(−8,12)$
$(3,0)$

Відповідь

ні
ні
ні
так
так

Визнати зв'язок між розв'язками нерівності та її графіком

У наступних вправах напишіть нерівність, показану затіненою областю.

Вправа $\PageIndex{7}$

Запишіть нерівність, показану графіком, з граничною лінією $y=3x−4$ .

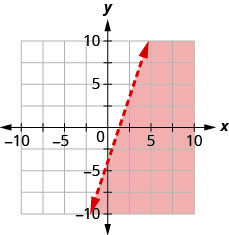
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює 3x мінус 4 наноситься як пунктирна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область праворуч від лінії затінена.$

Вправа $\PageIndex{8}$

Запишіть нерівність, показану графіком, з граничною лінією $y=2x−4$ .

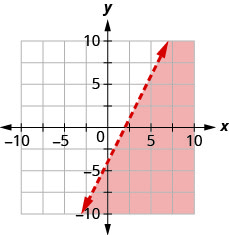
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює 2x мінус 4 будується як суцільна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінена.$

Відповідь: $y<2 x-4$

Вправа $\PageIndex{9}$

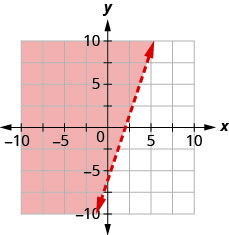
Запишіть нерівність, показану графіком, з граничною лінією $y=\frac{1}{2} x+1$

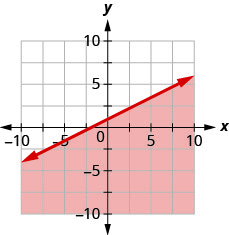
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативній половині х плюс 1 будується як суцільна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінена.$

Вправа $\PageIndex{10}$

Запишіть нерівність, показану графіком, з граничною лінією $y=-\frac{1}{3} x-2$

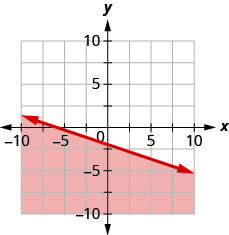
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативній третині х мінус 2 будується як суцільна лінія, що проходить від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

Відповідь: $y \leq-\frac{1}{3} x-2$

Вправа $\PageIndex{11}$

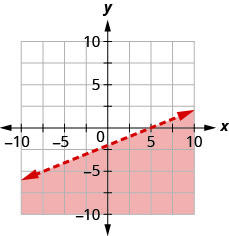
Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $x+y=5$ .

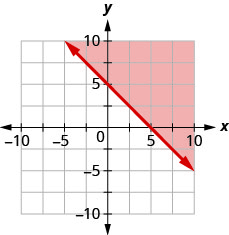
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія х плюс у дорівнює 5 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область над лінією затінюють.$

Вправа $\PageIndex{12}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $x+y=3$ .

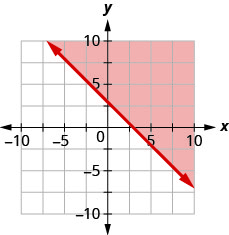
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія х плюс у дорівнює 3 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область над лінією затінюють.$

Відповідь: $x+y \geq 3$

Вправа $\PageIndex{13}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $2x+y=−4$ .

$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 2 х плюс у дорівнює негативному 4 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

Вправа $\PageIndex{14}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $x+2y=−2$ .

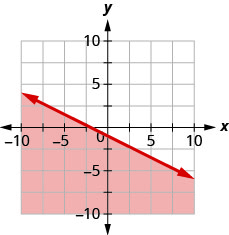
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія х плюс 2 y дорівнює негативному 2 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

Відповідь: $x+2 y \geq-2$

Вправа $\PageIndex{15}$

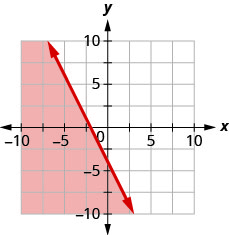
Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $3x−y=6$ .

$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 3 х мінус у дорівнює 6 наноситься як пунктирна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область зліва від лінії затінена.$

Вправа $\PageIndex{16}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $2x−y=4$ .

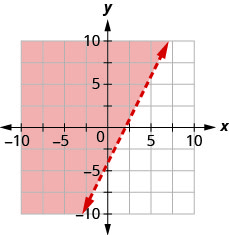
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 2 х мінус у дорівнює 4 наноситься як пунктирна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область зліва від лінії затінена.$

Відповідь: $2 x-y<4$

Вправа $\PageIndex{17}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $2x−5y=10$ .

$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 2 х мінус 5 у дорівнює 10 наноситься як пунктирна лінія, що тягнеться від нижнього лівого до верхнього праворуч. Область нижче лінії затінена.$

Вправа $\PageIndex{18}$

Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією $4x−3y=12$ .

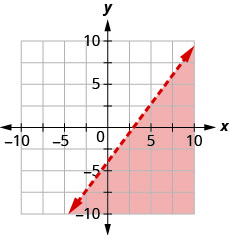
$На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 4 х мінус 3 у дорівнює 12 наноситься як пунктирна лінія, що тягнеться від нижнього лівого до верхнього праворуч. Область нижче лінії затінена.$

Відповідь: $4 x-3 y>12$

Лінійні нерівності графа

У наступних вправах проведіть графік кожної лінійної нерівності.

Вправа $\PageIndex{19}$

Графік лінійної нерівності $y>\frac{2}{3} x-1$

Вправа $\PageIndex{20}$

Графік лінійної нерівності $y<\frac{3}{5} x+2$

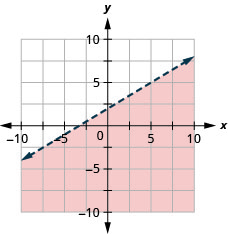
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює три п'ятих х плюс 2 наноситься як пунктирна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінена.$

Вправа $\PageIndex{21}$

Графік лінійної нерівності $y \leq-\frac{1}{2} x+4$

Вправа $\PageIndex{22}$

Графік лінійної нерівності $y \geq-\frac{1}{3} x-2$

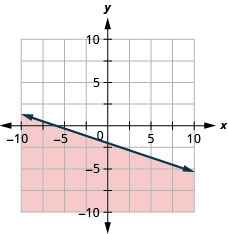
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативній третині х мінус 2 будується як суцільна лінія, що проходить від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

Вправа $\PageIndex{23}$

Графік лінійної нерівності $x-y \leq 3$

Вправа $\PageIndex{24}$

Графік лінійної нерівності $x-y \geq -2$

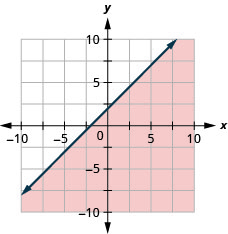
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія x мінус y дорівнює негативному 2 будується як суцільна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінена.$

Вправа $\PageIndex{25}$

Графік лінійної нерівності $4x+y>-4$

Вправа $\PageIndex{26}$

Графік лінійної нерівності $x+5y<-5$

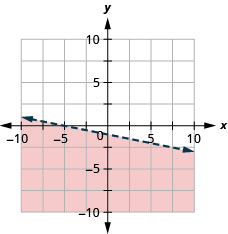
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія х плюс 5 у дорівнює негативний 5 будується як пунктирна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

Вправа $\PageIndex{27}$

Графік лінійної нерівності $3 x+2 y \geq-6$

Вправа $\PageIndex{28}$

Графік лінійної нерівності $4 x+2 y \geq-8$

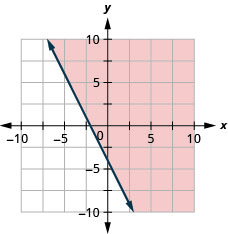
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 4 х плюс 2 у дорівнює негативний 8 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область праворуч від лінії затінена.$

Вправа $\PageIndex{29}$

Графік лінійної нерівності $y>4x$

Вправа $\PageIndex{30}$

Графік лінійної нерівності $y>x$

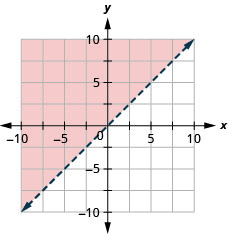
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює x наноситься як суцільна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область над лінією затінюють.$

Вправа $\PageIndex{31}$

Графік лінійної нерівності $y \leq-x$

Вправа $\PageIndex{32}$

Графік лінійної нерівності $y \leq-3 x$

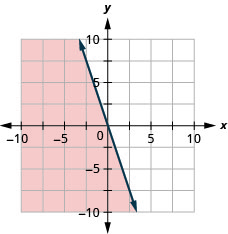
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 3 х наноситься як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область зліва від лінії затінена.$

Вправа $\PageIndex{33}$

Графік лінійної нерівності $y \geq-2$

Вправа $\PageIndex{34}$

Графік лінійної нерівності $y<-1$

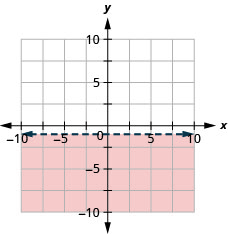
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 1 наноситься як пунктирна горизонтальна лінія. Область нижче лінії затінена.$

Вправа $\PageIndex{35}$

Графік лінійної нерівності $y<4$

Вправа $\PageIndex{36}$

Графік лінійної нерівності $y \geq 2$

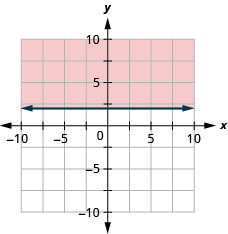
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює 2 наноситься як суцільна горизонтальна лінія. Область над лінією затінюють.$

Вправа $\PageIndex{37}$

Графік лінійної нерівності $x \leq 5$

Вправа $\PageIndex{38}$

Графік лінійної нерівності $x>-2$

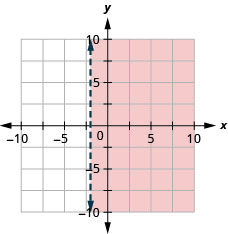
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія x дорівнює від'ємній 2 наноситься як пунктирна вертикальна лінія. Область праворуч від лінії затінена.$

Вправа $\PageIndex{39}$

Графік лінійної нерівності $x>-3$

Вправа $\PageIndex{40}$

Графік лінійної нерівності $x \leq 4$

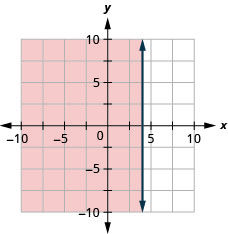
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія x дорівнює 4 наноситься як суцільна вертикальна лінія. Область зліва від лінії затінена.$

Вправа $\PageIndex{41}$

Графік лінійної нерівності $x-y<4$

Вправа $\PageIndex{42}$

Графік лінійної нерівності $x-y<-3$

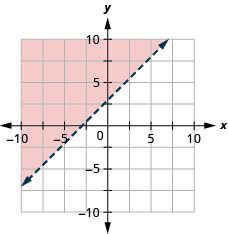
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія x мінус y дорівнює негативному 3 наноситься як пунктирна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область над лінією затінюють.$

Вправа $\PageIndex{43}$

Графік лінійної нерівності $y \geq \frac{3}{2} x$

Вправа $\PageIndex{44}$

Графік лінійної нерівності $y \leq \frac{5}{4} x$

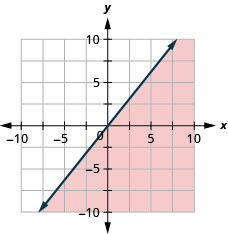
Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює п'яти четвертих х наноситься як суцільна лінія, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінена.$

Вправа $\PageIndex{45}$

Графік лінійної нерівності $y>-2 x+1$

Вправа $\PageIndex{46}$

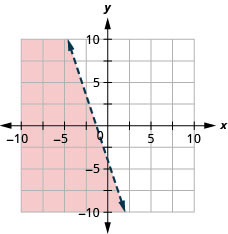
Графік лінійної нерівності $y<-3 x-4$

Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 3 х мінус 4 наноситься як пунктирна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область зліва від лінії затінена.$

Вправа $\PageIndex{47}$

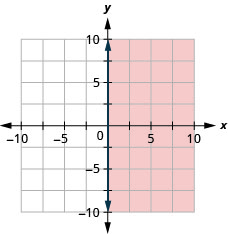
Графік лінійної нерівності $x \leq-1$

Вправа $\PageIndex{48}$

Графік лінійної нерівності $x \geq 0$

Відповідь: $На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія x дорівнює від'ємному 0 будується як суцільна вертикальна лінія вздовж осі y. Область праворуч від лінії затінена.$

Щоденна математика

Вправа $\PageIndex{49}$

Гроші. Джеррі хоче мати максимум 100 доларів готівки в касі, коли відкриється його церковний карнавал. У нього будуть купюри в 1 долар і купюри в 5 доларів. Якщо $x$ кількість купюр $y$ $1 і кількість $5 купюр, нерівність $x+5y \leq 100$ моделює ситуацію.

Графік нерівності.
Перерахуйте три розв'язки нерівності $x+5y \leq 100$ , де обидва $x$ і $y$ є цілими числами.

Вправа $\PageIndex{50}$

Шопінг. Тула має 20 доларів, щоб витратити на продаж б/у книг. Книги в твердій обкладинці коштують 2 долари, а книги в м'якій обкладинці коштують 0,50 долара. Якщо $x$ кількість книг у твердій палітурці Тула може купити і $y$ є кількість книг у м'якій обкладинці, яку вона може купити, то нерівність $2x+\frac{1}{2} y \leq 20$ моделює ситуацію.

Графік нерівності.
Перерахуйте три рішення нерівності $2x+\frac{1}{2} y \leq 20$ , де обидва $x$ і $y$ є цілими числами.

Відповідь

1.
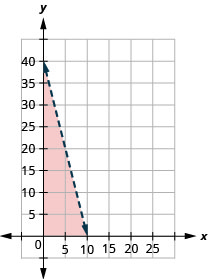
$На графіку показана координатна площина x y. Вісь x- працює від 0 до 20, а вісь y - від 0 до 30. Лінія 2 х плюс одна половина у дорівнює 20 будується як суцільна лінія, що тягнеться від верхнього лівого краю до нижнього правого. Область нижче лінії затінена.$

2. Відповіді будуть відрізнятися.

Письмові вправи

Вправа $\PageIndex{51}$

Лестер вважає, що розв'язком будь-якої нерівності зі $>$ знаком є область над лінією, а рішення будь-якої нерівності зі $<$ знаком - область нижче лінії. Чи правильно Лестер? Поясніть, чому чи чому ні.

Вправа $\PageIndex{52}$

Поясніть, чому на деяких графіках лінійних нерівностей межова лінія є суцільною, а в інших графах вона пунктирна.

Самостійна перевірка

а Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.

$Це таблиця, яка має чотири рядки і чотири стовпці. У першому рядку, який є рядком заголовка, клітинки читають зліва направо: «Я можу...», «впевнено», «з деякою допомогою» та «Ні-я не розумію!» Перший стовпець нижче «Я можу...» читає «перевірити рішення нерівності у двох змінних», «розпізнати зв'язок між розв'язками нерівності та її графіком» та «лінійні нерівності графа». Решта осередків порожні.$

б Що говорить вам цей контрольний список про ваше володіння цим розділом? Які кроки ви зробите для вдосконалення?

Практика робить досконалим

Вправа4.7E.1\PageIndex{1}

Вправа4.7E.2\PageIndex{2}

Вправа4.7E.3\PageIndex{3}

Вправа4.7E.4\PageIndex{4}

Вправа4.7E.5\PageIndex{5}

Вправа4.7E.6\PageIndex{6}

Вправа4.7E.7\PageIndex{7}

Вправа4.7E.8\PageIndex{8}

Вправа4.7E.9\PageIndex{9}

Вправа4.7E.10\PageIndex{10}

Вправа4.7E.11\PageIndex{11}

Вправа4.7E.12\PageIndex{12}

Вправа4.7E.13\PageIndex{13}

Вправа4.7E.14\PageIndex{14}

Вправа4.7E.15\PageIndex{15}

Вправа4.7E.16\PageIndex{16}

Вправа4.7E.17\PageIndex{17}

Вправа4.7E.18\PageIndex{18}

Вправа4.7E.19\PageIndex{19}

Вправа4.7E.20\PageIndex{20}

Вправа4.7E.21\PageIndex{21}

Вправа4.7E.22\PageIndex{22}

Вправа4.7E.23\PageIndex{23}

Вправа4.7E.24\PageIndex{24}

Вправа4.7E.25\PageIndex{25}

Вправа4.7E.26\PageIndex{26}

Вправа4.7E.27\PageIndex{27}

Вправа4.7E.28\PageIndex{28}

Вправа4.7E.29\PageIndex{29}

Вправа4.7E.30\PageIndex{30}

Вправа4.7E.31\PageIndex{31}

Вправа4.7E.32\PageIndex{32}

Вправа4.7E.33\PageIndex{33}

Вправа4.7E.34\PageIndex{34}

Вправа4.7E.35\PageIndex{35}

Вправа4.7E.36\PageIndex{36}

Вправа4.7E.37\PageIndex{37}

Вправа4.7E.38\PageIndex{38}

Вправа4.7E.39\PageIndex{39}

Вправа4.7E.40\PageIndex{40}

Вправа4.7E.41\PageIndex{41}

Вправа4.7E.42\PageIndex{42}

Вправа4.7E.43\PageIndex{43}

Вправа4.7E.44\PageIndex{44}

Вправа4.7E.45\PageIndex{45}

Вправа4.7E.46\PageIndex{46}

Вправа4.7E.47\PageIndex{47}

Вправа4.7E.48\PageIndex{48}

Щоденна математика

Вправа4.7E.49\PageIndex{49}

Вправа4.7E.50\PageIndex{50}

Письмові вправи

Вправа4.7E.51\PageIndex{51}

Вправа4.7E.52\PageIndex{52}

Самостійна перевірка

Вправа $\PageIndex{1}$

Вправа $\PageIndex{2}$

Вправа $\PageIndex{3}$

Вправа $\PageIndex{4}$

Вправа $\PageIndex{5}$

Вправа $\PageIndex{6}$

Вправа $\PageIndex{7}$

Вправа $\PageIndex{8}$

Вправа $\PageIndex{9}$

Вправа $\PageIndex{10}$

Вправа $\PageIndex{11}$

Вправа $\PageIndex{12}$

Вправа $\PageIndex{13}$

Вправа $\PageIndex{14}$

Вправа $\PageIndex{15}$

Вправа $\PageIndex{16}$

Вправа $\PageIndex{17}$

Вправа $\PageIndex{18}$

Вправа $\PageIndex{19}$

Вправа $\PageIndex{20}$

Вправа $\PageIndex{21}$

Вправа $\PageIndex{22}$

Вправа $\PageIndex{23}$

Вправа $\PageIndex{24}$

Вправа $\PageIndex{25}$

Вправа $\PageIndex{26}$

Вправа $\PageIndex{27}$

Вправа $\PageIndex{28}$

Вправа $\PageIndex{29}$

Вправа $\PageIndex{30}$

Вправа $\PageIndex{31}$

Вправа $\PageIndex{32}$

Вправа $\PageIndex{33}$

Вправа $\PageIndex{34}$

Вправа $\PageIndex{35}$

Вправа $\PageIndex{36}$

Вправа $\PageIndex{37}$

Вправа $\PageIndex{38}$

Вправа $\PageIndex{39}$

Вправа $\PageIndex{40}$

Вправа $\PageIndex{41}$

Вправа $\PageIndex{42}$

Вправа $\PageIndex{43}$

Вправа $\PageIndex{44}$

Вправа $\PageIndex{45}$

Вправа $\PageIndex{46}$

Вправа $\PageIndex{47}$

Вправа $\PageIndex{48}$

Вправа $\PageIndex{49}$

Вправа $\PageIndex{50}$

Вправа $\PageIndex{51}$

Вправа $\PageIndex{52}$