Skip to main content
LibreTexts - Ukrayinska

4.4: Розуміння нахилу лінії

  1. Last updated
  2. Save as PDF
  • Page ID
    58814

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • До кінця цього розділу ви зможете:
    • Використовуйте геоборди для моделювання схилу
    • Використовуйте\(m = \frac{\text{rise}}{\text{run}}\) для пошуку нахилу прямої з її графіка
    • Знайти нахил горизонтальних і вертикальних ліній
    • Використовуйте формулу нахилу, щоб знайти нахил прямої між двома точками
    • Графік лінії з заданою точкою і нахилом
    • Вирішіть програми нахилу
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Спростити:\(\frac{1 - 4}{8 - 2}\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.6.31
    2. Розділити:\(\frac{0}{4}, \frac{4}{0}\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.10.16.
    3. Спростити:\(\frac{15}{-3}, \frac{-15}{3}, \frac{-15}{-3}\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.6.4.

    Коли ви графуєте лінійні рівняння, ви можете помітити, що деякі лінії нахиляються вгору, коли вони йдуть зліва направо, а деякі лінії нахиляються вниз. Деякі лінії дуже круті, а деякі лінії більш плоскі. Що визначає, чи нахиляється лінія вгору або вниз або крута чи рівна?

    У математиці «нахил» лінії називається нахилом лінії. Поняття схилу має багато застосувань у реальному світі. Крок даху, клас шосе та пандус для інвалідного візка - це деякі приклади, де ви буквально бачите схили. А коли ви їдете на велосипеді, ви відчуваєте схил, коли ви накачуєте гору або берег вниз.

    У цьому розділі ми вивчимо поняття схилу.

    Використовуйте геоборди для моделювання схилу

    Геоборд - це дошка з сіткою з кілочків на ній. Використання гумок на геоборді дає нам конкретний спосіб моделювання ліній на координатній сітці. Розтягнувши гумку між двома кілочками на геоборді, ми можемо виявити, як знайти нахил лінії.

    Виконання діяльності з маніпулятивної математики «Вивчення схилу» допоможе вам краще зрозуміти нахил лінії. (Якщо це необхідно, замість геоборду можна використовувати графічний папір.)

    Почнемо з розтягування гумки між двома кілочками, як показано на малюнку\(\PageIndex{1}\).

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 4 і кілочком в стовпчику 4, ряду 2 натягується гумка, утворюючи лінію.
    Малюнок\(\PageIndex{1}\)

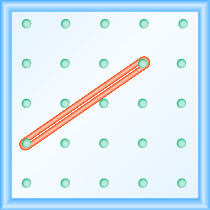
    Хіба це не схоже на лінію?

    Тепер простягаємо одну частину гумки прямо вгору від лівого кілочка і навколо третього кілочка, щоб зробити сторони прямокутного трикутника, як показано на малюнку\(\PageIndex{2}\)

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпці 1, ряду 2, кілочком в стовпці 1, рядком 1, рядком 4 і кілочком в стовпчику 4, ряду 2, утворюючи прямокутний трикутник. Кілок 1, 2 - це вершина кута 90 градусів, тоді як лінія між кілочками 1, 4 і 4, 2 утворює гіпотенузу трикутника.
    Малюнок\(\PageIndex{2}\)

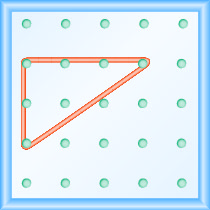
    Обережно робимо кут 90º навколо третього кілочка, тому одна з новоутворених ліній вертикальна, а інша - горизонтальна.

    Щоб знайти нахил лінії, заміряємо відстань по вертикальній і горизонтальній сторонам трикутника. Вертикальна відстань називається підйомом, а горизонтальна відстань називається пробігом, як показано на малюнку\(\PageIndex{3}\).

    На цій ілюстрації є дві перпендикулярні лінії зі стрілками. Перша лінія тягнеться прямо вгору і позначається «підйом». Друга стрілка простягається прямо вправо і має позначку «бігти».
    Малюнок\(\PageIndex{3}\)

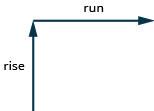
    Якщо наша геоборд і гумка виглядають так само, як показано на малюнку\(\PageIndex{4}\), підйом дорівнює 2. Гумка йде вгору на 2 одиниці. (Кожен простір - це одна одиниця.)

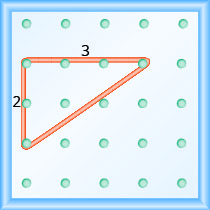
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком у стовпці 1, ряду 2 натягується гумка, кілочок у стовпці 1, ряд 4 та кілочок у стовпці 4, ряд 2, утворюючи прямокутний трикутник, де кілочок 1, 2 є вершиною кута 90 градусів, а лінія між кілочком 1, 4 і кілочком 4, 2 утворює гіпотенузу. Лінія між кілочком 1, 2 і кілочком 1, 4 маркується «2». Лінія між кілочком 1, 2 і кілочком 4, 2 має маркування «3».
    Малюнок\(\PageIndex{4}\)

    Підйом на цій геоборді дорівнює 2, так як гумка піднімається вгору на дві одиниці.

    Що таке пробіг?

    Гумка йде через 3 одиниці. Прогін дорівнює 3 (див. Рис.\(\PageIndex{4}\)).

    Ухил лінії - це відношення підйому до прогону. У математиці його завжди називають буквою м.

    НАХИЛ ЛІНІЇ

    Нахил лінії лінії дорівнює\(m = \frac{\text{rise}}{\text{run}}\).

    Підйом вимірює вертикальну зміну, а пробіг вимірює зміну горизонталі між двома точками на лінії.

    Який нахил лінії на геоборді на малюнку\(\PageIndex{4}\)?

    \[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{2}{3} \end{aligned}\]

    Лінія має нахил\(\frac{2}{3}\). Це означає, що лінія піднімається на 2 одиниці на кожні 3 одиниці пробігу.

    Коли ми працюємо з геобордами, це гарна ідея, щоб отримати звичку починати з кілочка зліва і підключатися до кілочка праворуч. Якщо підйом йде вгору, це позитивно, а якщо воно знижується, це негативно. Біг буде йти зліва направо і бути позитивним.

    Вправа\(\PageIndex{1}\)

    Який нахил лінії на геоборді показаний?

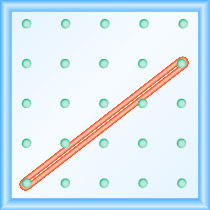
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 5 і кілочком в стовпчику 5, ряду 2 натягується гумка, утворюючи лінію.

    Відповідь

    Скористайтеся визначенням ухилу:\(m = \frac{\text{rise}}{\text{run}}\).

    Почніть з лівого кілочка і порахуйте пробіли вгору і вправо, щоб досягти другого кілочка.

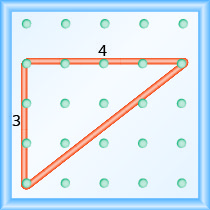
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 2 натягується гумка, кілочок в стовпці 1, ряд 5 і кілочок в стовпчику 5, ряд 2, утворюючи прямокутний трикутник. Кілок 1, 2 утворює вершину кута 90 градусів, а лінія від кілочка 1, 5 до кілочка 5, 2 утворює гіпотенузу трикутника. Лінія від 1, 2 кілочка до кілочка 1, 5 має маркування «3». Лінія від 1, 2 кілочка до кілочка 5, 2 має маркування «4».

    \[\begin{array}{ll} {\text { The rise is } 3 .} &{m=\frac{3}{\operatorname{rnn}}} \\ {\text { The run is 4. }} & {m=\frac{3}{4}} \\ { } & {\text { The slope is } \frac{3}{4} \text { . }}\end{array}\]

    Це означає, що лінія піднімається на 3 одиниці за кожні 4 одиниці пробігу.

    Вправа\(\PageIndex{2}\)

    Який нахил лінії на геоборді показаний?

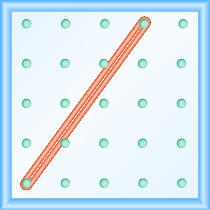
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 5 і кілочком в стовпчику 4, ряду 1 натягується гумка, утворюючи лінію.

    Відповідь

    \(\frac{4}{3}\)

    Вправа\(\PageIndex{3}\)

    Який нахил лінії на геоборді показаний?

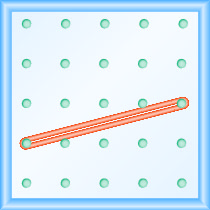
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 4 і кілочком в стовпці 5, ряду 3 натягується гумка, утворюючи лінію.

    Відповідь

    \(\frac{1}{4}\)

    Вправа\(\PageIndex{4}\)

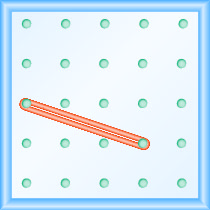
    Який нахил лінії на геоборді показаний?

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 3 і кілочком в стовпчику 4, ряду 4 натягується гумка, утворюючи лінію.

    Відповідь

    Скористайтеся визначенням ухилу:\(m = \frac{\text{rise}}{\text{run}}\).

    Почніть з лівого кілочка і порахуйте одиниці вниз і вправо, щоб досягти другого кілочка.

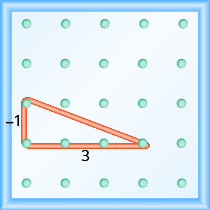
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 3 натягується гумка, кілочок в стовпці 1, ряд 4 і кілочок в стовпці 4, ряд 4, утворюючи прямокутний трикутник. Кілок 1, 3 утворює вершину кута 90 градусів, а лінія від кілочка 1, 4 до кілочка 4, 4 утворює гіпотенузу трикутника. Лінія від кілочка 1, 3 до кілочка 1, 4 позначається як «негативний 1». Лінія від 1, 4 кілочка до кілочка 4, 4 має маркування «3».

    \[\begin{array}{ll}{\text { The rise is }-1 .} & {m=\frac{-1}{\operatorname{run}}} \\ {\text { The run is } 3 .} & {m=\frac{-1}{3}} \\ {} & {m=-\frac{1}{3}} \\ {} &{\text { The slope is }-\frac{1}{3}}\end{array}\]

    Це означає, що лінія скидає 1 одиницю на кожні 3 одиниці пробігу.

    Вправа\(\PageIndex{5}\)

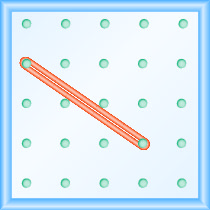
    Що таке ухил лінії на геобаду?

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 2 і кілочком в стовпчику 4, ряду 4 натягується гумка, утворюючи лінію.

    Відповідь

    \(-\frac{2}{3}\)

    Вправа\(\PageIndex{6}\)

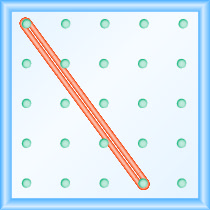
    Що таке ухил лінії на геобаду?

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 1 і кілочком в стовпчику 4, ряду 5 натягується гумка, утворюючи лінію.

    Відповідь

    \(-\frac{4}{3}\)

    Зверніть увагу, що у\(\PageIndex{1}\) Вправи нахил є позитивним, а у\(\PageIndex{4}\) Вправи нахил негативний. Чи помічаєте ви якусь різницю в двох рядках, показаних на малюнку (а) та малюнку (b)?

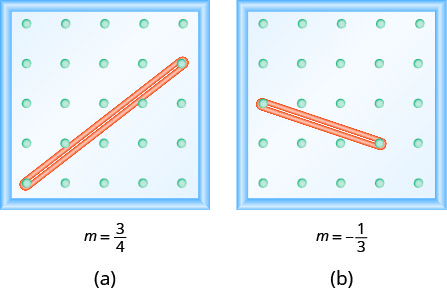
    На малюнку показані дві сітки рівномірно розташованих кілочків, одна з яких позначена (а) і одна з маркованих (b). У кожній сітці 5 стовпчиків і 5 рядів кілочків. У (а) сітці між кілочком в стовпчику 1, ряду 5 і кілочком в стовпчику 5, ряду 2 натягується гумка, утворюючи лінію. Нижче цієї сітки знаходиться нахил лінії, визначеної як m дорівнює 3 четвертих. У (б) сітці між кілочком в стовпчику 1, ряду 3 і кілочком в стовпчику 4, ряду 4 натягується гумка, утворюючи лінію. Під цією сіткою знаходиться нахил лінії, визначеної як m дорівнює від'ємній 1 третині.
    Малюнок\(\PageIndex{5}\)

    Ми «читаємо» рядок зліва направо так само, як ми читаємо слова англійською мовою. Коли ви читаєте зліва направо, рядок на малюнку (а) піднімається вгору; він має позитивний нахил. Лінія на малюнку (b) йде вниз; вона має негативний нахил.

    ПОЗИТИВНІ І НЕГАТИВНІ НАХИЛИ
    На малюнку зображені дві лінії пліч-о-пліч. Лінія зліва - діагональна лінія, яка піднімається зліва направо. Він має маркування «Позитивний нахил». Лінія праворуч - діагональна лінія, яка опускається зліва направо. Він має маркування «Негативний нахил».
    Малюнок\(\PageIndex{6}\)
    Вправа\(\PageIndex{7}\)

    Використовуйте геоборд для моделювання лінії з нахилом\(\frac{1}{2}\).

    Відповідь

    Для моделювання лінії на геоборді нам потрібні підйом і пробіг.

    \(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{1}{2} \text { . }} &{ \frac{1}{2} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } 1 \text { and the run is } 2 \text { . }} \\ {\text { Start at a peg in the lower left of the geoboard. }} \\ {\text { Stretch the rubber band up } 1 \text { unit, and then right } 2 \text { units. }}\end{array}\)

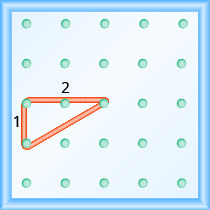
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпці 1, ряду 3 натягується гумка, кілочок в стовпці 1, ряд 4 і кілочок в стовпці 3, ряд 3, утворюючи прямокутний трикутник. Кілок 1, 3 утворює вершину кута 90 градусів, а лінія від кілочка 1, 4 до кілочка 3, 3 утворює гіпотенузу трикутника. Лінія від кілочка 1, 3 до кілочка 1, 4 маркується «1». Лінія від 1, 3 кілочка до кілочка 3, 3 маркується «2».

    Гіпотенуза прямокутного трикутника, утвореного гумкою, являє собою лінію, нахил якої дорівнює\(\frac{1}{2}\).

    Вправа\(\PageIndex{8}\)

    Змоделюйте ухил\(m = \frac{1}{3}\). Намалюйте картинку, щоб показати свої результати.

    Відповідь

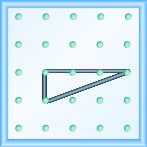
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 3 натягується гумка, кілочок в стовпчику 2, ряд 4 і кілочок в стовпці 5, ряд 3, утворюючи прямокутний трикутник. Кілок 2, 3 утворює вершину кута 90 градусів, а лінія від кілочка 2, 4 до кілочка 5, 3 утворює гіпотенузу трикутника.

    Вправа\(\PageIndex{9}\)

    Змоделюйте ухил\(m = \frac{3}{2}\). Намалюйте картинку, щоб показати свої результати.

    Відповідь

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 1, кілочком в стовпчику 1, рядком 4 і кілочком в стовпчику 3, ряду 1, утворюючи прямокутний трикутник. 1, 1 кілочок утворює вершину кута 90 градусів, а лінія від кілочка 1, 4 до кілочка 3, 1 утворює гіпотенузу трикутника.

    Вправа\(\PageIndex{10}\)

    Використовуйте геоборд для моделювання лінії з нахилом\(\frac{-1}{4}\).

    Відповідь

    \(\begin{array}{ll} {\text { Use the slope formula. }} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text { Replace } m \text { with } \frac{-1}{4} \text { . }} &{ \frac{-1}{4} = \frac{\text{rise}}{\text{run}}}\\ {\text { So, the rise is } -1 \text { and the run is } 4 \text { . }} \\ {\text { Since the rise is negative, we choose a starting peg on the upper left that will give us room to count down.}} \\ {\text { We stretch the rubber band down } 1 \text { unit, and then right } 4 \text { units. }}\end{array}\)

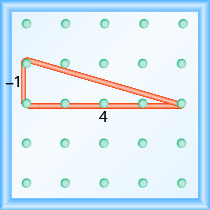
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 2, кілочком в стовпці 1, рядком 3 і кілочком в стовпчику 5, ряду 3, утворюючи прямокутний трикутник. Кілок 1, 3 утворює вершину кута 90 градусів, а лінія від кілочка 1, 2 до кілочка 5, 3 утворює гіпотенузу трикутника. Лінія від кілочка 1, 2 до кілочка 1, 3 позначається як «негативний 1». Лінія від кілочка 1, 3 до кілочка 5, 3 маркується «4».

    Гіпотенуза прямокутного трикутника, утвореного гумкою, являє собою лінію, нахил якої дорівнює\(\frac{-1}{4}\).

    Вправа\(\PageIndex{11}\)

    Змоделюйте ухил\(m = \frac{-2}{3}\). Намалюйте картинку, щоб показати свої результати.

    Відповідь

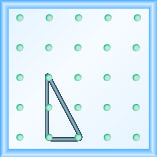
    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 2, ряду 3 натягується гумка, кілочок в стовпці 2, ряд 5 і кілочок в стовпці 3, ряд 5, утворюючи прямокутний трикутник. Кілок 2, 5 утворює вершину кута 90 градусів, а лінія від кілочка 2, 3 до кілочка 3, 5 утворює гіпотенузу трикутника.

    Вправа\(\PageIndex{12}\)

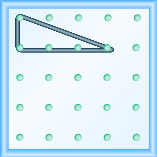
    Змоделюйте ухил\(m = \frac{-1}{3}\). Намалюйте картинку, щоб показати свої результати.

    Відповідь

    На малюнку зображена сітка з рівномірно розташованих кілочків. Є 5 стовпчиків і 5 рядів кілочків. Між кілочком в стовпчику 1, ряду 1, кілочком в стовпці 1, рядком 2 і кілочком в стовпчику 4, ряду 2, утворюючи прямокутний трикутник. Кілок 1, 2 утворює вершину кута 90 градусів, а лінія від кілочка 1, 1 до кілочка 4, 2 утворює гіпотенузу трикутника.

    \(m = \frac{\text{rise}}{\text{run}}\)Використовувати для пошуку нахилу прямої з її графіка

    Тепер ми розглянемо деякі графіки на xy-координатної площині і подивимося, як знайти їх нахили. Метод буде дуже схожий на те, що ми щойно змоделювали на наших геобордах.

    Щоб знайти ухил, треба порахувати підйом і пробіг. Але з чого ми починаємо?

    Ми знаходимо дві точки на лінії, координати яких цілі числа. Потім ми починаємо з точки зліва і накидаємо прямокутний трикутник, щоб ми могли порахувати підйом і бігти.

    Вправа\(\PageIndex{13}\):

    Знайдіть нахил показаної лінії.

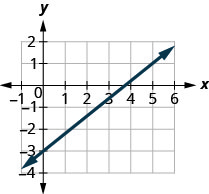
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 6, а вісь y - від негативних 4 до 2. Через точки (0, від'ємний 3) і (5, 1) проходить лінія.

    Відповідь

    Ця таблиця складається з трьох стовпців і чотирьох рядків. Перший ряд говорить: «Крок 1. Знайдіть дві точки на графіку, координати яких є цілими числами. Позначки (0, негативні 3) і (5, 1)». Праворуч знаходиться лінія, зображена на координатній площині x y. Вісь X площини проходить від негативного 1 до 6. Вісь Y площини проходить від негативних 4 до 2. 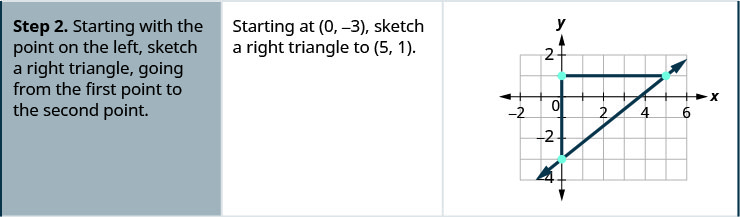Виставляються точки (0, від'ємні 3) і (5, 1).Другий ряд говорить: «Крок 2. Починаючи з точки зліва, накидайте прямокутний трикутник, що йде від першої точки до другої точки. Починаючи з (0, від'ємний 3), намалюйте прямокутний трикутник до (5, 1)». На графіку справа наноситься додаткова точка в (0, 1). Три точки утворюють прямокутний трикутник, причому лінія від (0, негативна 3) до (5, 1) утворює гіпотенузу, а лінії від (0, негативні 3) до (0, 1) і (0, 1) до (5, 1) утворюють катети.Третій ряд потім говорить: «Крок 3. Підрахуйте підйом і біг по ніжках трикутника». Підйом дорівнює 4, а пробіг - 5.Четвертий ряд говорить: «Крок 4. Візьміть співвідношення підйому до бігу, щоб знайти схил. Скористайтеся формулою нахилу. Підставте значення підйому і бігу». Праворуч - формула нахилу, m дорівнює підйому, поділеному на пробіг. Ухил лінії 4 ділиться на 5, або чотири п'ятих. Це означає, що y збільшує 4 одиниці, оскільки x збільшує 5 одиниць.

    Вправа\(\PageIndex{14}\)

    Знайдіть нахил показаної лінії.

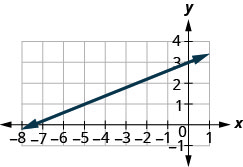
    Графік показує координатну площину x y. Вісь x проходить від негативного 8 до 1, а вісь y - від негативного 1 до 4. Через точки (від'ємні 5, 1) і (0, 3) проходить лінія.

    Відповідь

    \(\frac{2}{5}\)

    Вправа\(\PageIndex{15}\)

    Знайдіть нахил показаної лінії.

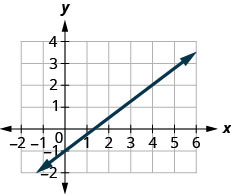
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 5, а вісь y - від негативного 2 до 4. Через точки (0, від'ємний 1) і (4, 2) проходить лінія.

    Відповідь

    \(\frac{3}{4}\)

    ЗНАЙТИ НАХИЛ ЛІНІЇ З ЇЇ ГРАФІКА
    1. Знайдіть дві точки на лінії, координати яких є цілими числами.
    2. Починаючи з точки зліва, накидайте прямокутний трикутник, що йде від першої точки до другої точки.
    3. Підрахуйте підйом і біг на ніжках трикутника.
    4. Візьміть співвідношення підйому до бігу, щоб знайти схил,\(m = \frac{\text{rise}}{\text{run}}\).
    Вправа\(\PageIndex{16}\)

    Знайдіть нахил показаної лінії.

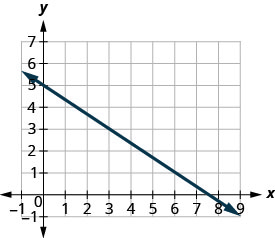
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 9, а вісь y - від негативного 1 до 7. Через точки (0, 5), (3, 3) і (6, 1) проходить лінія.

    Відповідь
    Знайдіть дві точки на графіку, координати яких є цілими числами. (0,5) і (3,3)
    Яка точка знаходиться зліва? (0,5)
    Починаючи з (0,5), намалюйте прямокутний трикутник до (3,3). .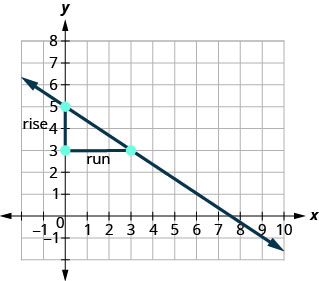
    Підрахуйте підйом — він негативний. Підйом дорівнює −2.
    Підрахуйте пробіг. Пробіг дорівнює 3.
    Скористайтеся формулою нахилу. \(m = \frac{\text{rise}}{\text{run}}\)
    Підставляємо значення підйому і бігу. \(m = \frac{-2}{3}\)
    Спростити. \(m = -\frac{2}{3}\)
      Ухил лінії дорівнює\(-\frac{2}{3}\).

    Так y збільшується на 3 одиниці, оскільки xx зменшується на 2 одиниці.

    Що робити, якщо ми використали точки (−3,7) та (6,1), щоб знайти нахил прямої?

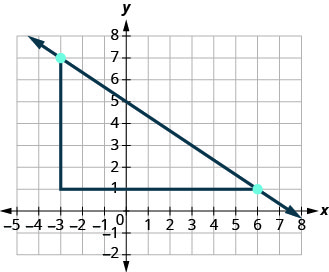
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 3, 7) і (6, 1) проходить лінія. Додаткова точка наноситься на (мінус 3, 1). Три точки утворюють прямокутний трикутник, причому лінія від (негативна 3, 7) до (6, 1) утворює гіпотенузу, а лінії від (негативні 3, 7) до негативних 1, 7) і від (негативні 1, 7) до (6, 1) утворюють катети.

    Підйом буде −6, а пробіг - 9. Потім\(m = \frac{-6}{9}\), і це спрощує\(m = -\frac{2}{3}\). Пам'ятайте, що не має значення, які точки ви використовуєте - нахил лінії завжди однаковий.

    Вправа\(\PageIndex{17}\)

    Знайдіть нахил показаної лінії.

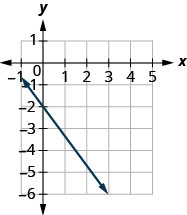
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 5, а вісь y - від негативного 6 до 1. Через точки (0, від'ємний 2) і (3, від'ємний 6) проходить лінія.

    Відповідь

    \(-\frac{4}{3}\)

    Вправа\(\PageIndex{18}\)

    Знайдіть нахил показаної лінії.

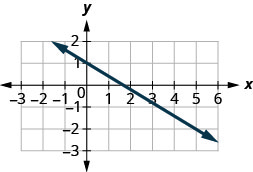
    Графік показує координатну площину x y. Вісь x проходить від негативних 3 до 6, а вісь y - від негативних 3 до 2. Через точки (0, 1) і (5, від'ємна 2) проходить лінія.

    Відповідь

    \(-\frac{3}{5}\)

    В останніх двох прикладах рядки мали y -перехоплення з цілими значеннями, тому було зручно використовувати y -intercept як одну з точок для пошуку нахилу. У наступному прикладі y -intercept є дріб. Замість того, щоб використовувати цю точку, ми будемо шукати дві інші точки, координати яких цілі числа. Це полегшить розрахунки ухилу.

    Вправа\(\PageIndex{19}\)

    Знайдіть нахил показаної лінії.

    Графік показує координатну площину x y. Вісь x працює від 0 до 8, а вісь y - від 0 до 7. Через точки (2, 3) і (7, 6) проходить лінія.

    Відповідь
    Знайдіть дві точки на графіку, координати яких є цілими числами. (2,3) і (7,6)
    Яка точка знаходиться зліва? (2,3)
    Починаючи з (2,3), намалюйте прямокутний трикутник до (7,6). .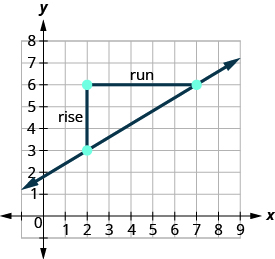
    Підрахуйте підйом. Підйом дорівнює 3.
    Підрахуйте пробіг. Пробіг дорівнює 5.
    Скористайтеся формулою нахилу. \(m = \frac{\text{rise}}{\text{run}}\)
    Підставляємо значення підйому і бігу. \(m = \frac{3}{5}\)
      Ухил лінії дорівнює\(\frac{3}{5}\).

    Це означає, що y збільшує 5 одиниць, оскільки x збільшує 3 одиниці.

    Коли ми використовували геоборди, щоб ввести поняття нахилу, ми сказали, що ми завжди будемо починати з точки зліва і рахувати підйом і пробіг, щоб дістатися до точки праворуч. Таким чином, пробіг завжди був позитивним, і підйом визначав, чи нахил був позитивним чи негативним.

    Що буде, якби ми почали з точки праворуч?

    Давайте знову використаємо точки (2,3) і (7,6), але зараз почнемо з (7,6).

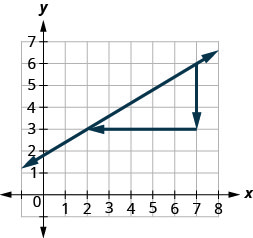
    Графік показує координатну площину x y. Вісь x - працює від 0 до 8. Вісь y працює від 0 до 7. Через точки (2, 3) і (7, 6) проходить лінія. Додаткова точка наноситься на (7, 3). Три точки утворюють прямокутний трикутник, причому лінія від (2, 3) до (7, 6) утворює гіпотенузу, а лінії від (2, 3) до (7, 3) і від (7, 3) до (7, 6) утворюють катети.
    \(\begin{array}{ll} {\text {Count the rise.}} &{\text{The rise is −3.}} \\ {\text {Count the run. It goes from right to left, so}} &{\text {The run is−5.}} \\{\text{it is negative.}} &{}\\ {\text {Use the slope formula.}} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{Substitute the values of the rise and run.}} &{m = \frac{-3}{-5}} \\{} &{\text{The slope of the line is }\frac{3}{5}}\\ \end{array}\)
    Неважливо, з чого ви починаєте - нахил лінії завжди однаковий.
    Вправа\(\PageIndex{20}\)

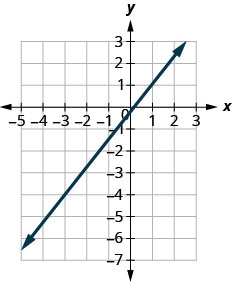
    Знайдіть нахил показаної лінії.

    Графік показує координатну площину x y. Вісь x проходить від негативних 4 до 2, а вісь y - від негативних 6 до 2. Через точки (від'ємні 3, 4) і (1, 1) проходить лінія.

    Відповідь

    \(\frac{5}{4}\)

    Вправа\(\PageIndex{21}\)

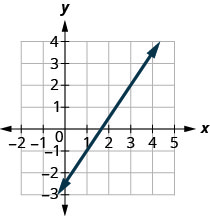
    Знайдіть нахил показаної лінії.

    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 4, а вісь y - від негативного 2 до 3. Через точки (1, від'ємний 1) і (3, 2) проходить лінія.

    Відповідь

    \(\frac{3}{2}\)

    Знайти нахил горизонтальних і вертикальних ліній

    Ви пам'ятаєте, що особливого було в горизонтальних і вертикальних лініях? Їх рівняння мали лише одну змінну.

    \[\begin{array}{ll}{\textbf {Horizontal line } y=b} & {\textbf {Vertical line } x=a} \\ {y \text { -coordinates are the same. }} & {x \text { -coordinates are the same. }}\end{array}\]

    Так як же знайти нахил горизонтальної лінії y=4y=4? Одним з підходів було б намалювати горизонтальну лінію, знайти дві точки на ній і підрахувати підйом і пробіг. Давайте подивимося, що станеться, коли ми це зробимо.

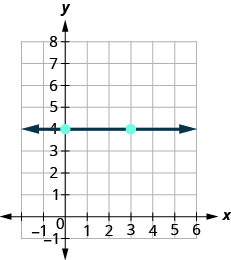
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 5, а вісь y - від негативного 1 до 7. Через точки (0, 4) і (3, 4) проходить лінія.
    Малюнок\(\PageIndex{7}\)

    \(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 0.}} \\ {\text {What is the run?}} & {\text {The run is 3.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {} &{m = \frac{0}{3}} \\ {\text{What is the slope?}} &{m = 0} \\ {} &{\text{The slope of the horizontal line y = 4 is 0.}} \end{array}\)

    Всі горизонтальні лінії мають нахил 0. Коли y -координати однакові, підйом дорівнює 0.

    НАХИЛ ГОРИЗОНТАЛЬНОЇ ЛІНІЇ

    Нахил горизонтальної лінії, y=b, дорівнює 0.

    Пол вашої кімнати горизонтальний. Його ухил дорівнює 0. Якщо ви акуратно поклали кульку на підлогу, він би не скотився.

    Тепер ми розглянемо вертикальну лінію, лінію.

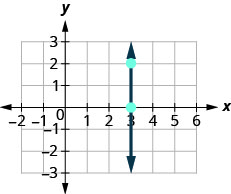
    Графік показує координатну площину x y. Вісь x проходить від негативного 1 до 5, а вісь y - від негативного 2 до 2. Через точки (3, 0) і (3, 2) проходить лінія.
    Малюнок\(\PageIndex{8}\)

    \(\begin{array}{ll} {\text {What is the rise?}} & {\text {The rise is 2.}} \\ {\text {What is the run?}} & {\text {The run is 0.}}\\ {} &{m = \frac{\text{rise}}{\text{run}}} \\ {\text{What is the slope?}} &{m = \frac{2}{0}} \end{array}\)

    Але ми не можемо розділити на 0. Ділення на 0 не визначено. Отже, ми говоримо, що нахил вертикальної лінії x = 3x=3 не визначено.

    Нахил будь-якої вертикальної лінії не визначено. Коли x -координати рядка однакові, прогін дорівнює 0.

    НАХИЛ ВЕРТИКАЛЬНОЇ ЛІНІЇ

    Нахил вертикальної лінії, x=a, не визначено.

    Вправа\(\PageIndex{22}\)

    Знайдіть нахил кожної лінії:

    ⓐ x=8 ⓑ y=−5.

    Відповідь

    ⓐ x=8
    Це вертикальна лінія.
    Його нахил невизначений.

    ⓑ y=−5
    Це горизонтальна лінія.
    Він має нахил 0.

    Вправа\(\PageIndex{23}\)

    Знайти нахил прямої: x=−4.

    Відповідь

    невизначений

    Вправа\(\PageIndex{24}\)

    Знайдіть нахил лінії: y=7.

    Відповідь

    0

    КОРОТКИЙ ПОСІБНИК ПО УХИЛАХ ЛІНІЙ
    На цьому малюнку зображені чотири лінії зі стрілками. Перша лінія піднімається вгору і біжить вправо. Вона має позитивний ухил. Друга лінія опускається вниз і біжить вправо. Вона має негативний нахил. Третя лінія ні піднімається, ні опускається, простягаючись горизонтально в будь-яку сторону. Вона має ухил в нуль. Четверта лінія повністю вертикальна, один кінець піднімається вгору, а інший піднімається вниз, бігаючи ні вліво, ні вправо. Вона має невизначений ухил.
    Малюнок\(\PageIndex{9}\)

    Пам'ятайте, що ми «читаємо» рядок зліва направо, так само, як ми читаємо написані слова англійською мовою.

    Використовуйте формулу нахилу, щоб знайти нахил лінії між двома точками

    Виконання діяльності з маніпулятивної математики «Нахил ліній між двома точками» допоможе вам краще зрозуміти, як знайти нахил лінії між двома точками.

    Іноді нам потрібно знайти нахил лінії між двома точками, коли у нас немає графіка, щоб відрахувати підйом і пробіг. Ми могли б побудувати точки на папері сітки, потім підрахувати підйом і пробіг, але, як ми побачимо, є спосіб знайти схил без графіки. Перш ніж ми дійдемо до нього, нам потрібно ввести деякі алгебраїчні позначення.

    Ми бачили, що впорядкована пара (x, y) дає координати точки. Але коли ми працюємо з ухилами, ми використовуємо два пункти. Як можна використовувати один і той же символ (x, y) для представлення двох різних точок? Математики використовують індекси для розрізнення точок.

    \[\begin{array}{ll}{\left(x_{1}, y_{1}\right)} & {\text { read }^{‘} x \text { sub } 1, y \text { sub } 1^{'}} \\ {\left(x_{2}, y_{2}\right)} & {\text { read }^{‘} x \text { sub } 2, y \text { sub } 2^{’}}\end{array}\]

    Використання індексів в математиці дуже схоже на використання ініціалів прізвища в початковій школі. Може бути, ви пам'ятаєте Лауру К. і Лору М. у своєму третьому класі?

    Ми будемо використовувати\(\left(x_{1}, y_{1}\right)\) для виявлення першої точки і\(\left(x_{2}, y_{2}\right)\) для виявлення другої точки.

    Якби у нас було більше двох точок, ми могли б використовувати\(\left(x_{3}, y_{3}\right)\)\(\left(x_{4}, y_{4}\right)\), і так далі.

    Давайте подивимося, як підйом і біг співвідносяться з координатами двох точок, по-іншому поглянувши на нахил лінії між точками (2,3) і (7,6).

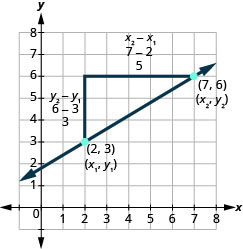
    Графік показує координатну площину x y. Осі x і y проходять від 0 до 7. Через точки (2, 3) і (7, 6) проходить лінія, які нанесені і маркуються. Впорядкована пара (2, 3) позначається (x індекс 1, y індекс 1). Впорядкована пара (7, 6) позначається (x індекс 2, y індекс 2). Додаткова точка наноситься на (2, 6). Три точки утворюють прямокутний трикутник, причому лінія від (2, 3) до (7, 6) утворює гіпотенузу, а лінії від (2, 3) до (2, 6) і від (2, 6) до (7, 6) утворюють катети. Перший відрізок, від (2, 3) до (2, 6) позначається у індексу 2 мінус y індекс 1, 6 мінус 3 та 3. Другий крок, від (2, 3) до (7, 6), позначений x індекс 2 мінус х індекс 1, y мінус 2 і 5.
    Малюнок\(\PageIndex{10}\)

    Оскільки у нас є дві точки, ми будемо використовувати індексні позначення,\(\left( \begin{array}{c}{x_{1}, y_{1}} \\ {2,3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {7,6}\end{array}\right)\).

    На графіку ми порахували підйом 3 і пробіг 5.

    Зверніть увагу, що підйом 3 можна знайти, віднімаючи y -координати 6 і 3.

    \[3=6-3\]

    А пробіг 5 можна знайти, віднімаючи x -координати 7 і 2.

    \[5 = 7 - 2\]

    Ми знаємо\(m = \frac{\text{rise}}{\text{run}}\). Отже\(m = \frac{3}{5}\).

    Переписуємо підйом і біжимо, вставивши координати\(m = \frac{6-3}{7-2}\)

    Але 6 - y2, y -координата другої точки і 3 - y1, y -координата першої точки.

    Таким чином, ми можемо переписати нахил, використовуючи індексні позначення. \(m = \frac{y2-y1}{7-2}\)

    Також 7 дорівнює x2, x -координата другої точки і 2 дорівнює x1, x -координата першої точки.

    Отже, знову ж таки, переписуємо нахил, використовуючи індексні позначення. \(m = \frac{y2-y1}{x2-x1}\)

    Ми показали, що\(m = \frac{y2-y1}{x2-x1}\) це дійсно інша версія\(m = \frac{\text{rise}}{\text{run}}\). Ми можемо використовувати цю формулу, щоб знайти нахил прямої, коли у нас є дві точки на лінії.

    ФОРМУЛА НАХИЛУ

    Нахил лінії між двома точками\(\left(x_{1}, y_{1}\right)\) і\(\left(x_{2}, y_{2}\right)\) становить

    \[m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\]

    Це формула нахилу.

    Ухил буває:

    \[\begin{array}{c}{y \text { of the second point minus } y \text { of the first point }} \\ {\text { over }} \\ {x \text { of the second point minus } x \text { of the first point. }}\end{array}\]

    Вправа\(\PageIndex{25}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої між точками (1,2) і (4,5).

    Відповідь

    \(\begin{array} {ll} {\text{We’ll call (1,2) point #1 and (4,5) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {1,2}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {4,5}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{5-2}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{5-2}{4-1}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{3}{3}} \\{\text{Simplify.}} &{m = 1} \end{array}\)

    Підтвердимо це, підраховуючи нахил на графіку за допомогою\(m = \frac{\text{rise}}{\text{run}}\).

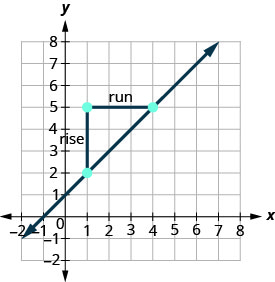
    На графіку показана координатна площина x y. Осі x та y площини проходять від 0 до 7. Через точки (1, 2) і (4, 5) проходить лінія, які наносяться. Додаткова точка наноситься на (1, 5). Три точки утворюють прямокутний трикутник, причому лінія від (1, 2) до (4, 5) утворює гіпотенузу, а лінії від (1, 2) до (1, 5) і від (1, 5) до (4, 5) утворюють катети. Нога від (1, 2) до (1, 5) позначається «підйом», а нога від (1, 5) до (4, 5) маркується «бігти».

    Не має значення, яку точку ви називаєте точкою #1 і яку ви називаєте точку #2. Ухил буде однаковим. Спробуйте зробити розрахунок самостійно.

    Вправа\(\PageIndex{26}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої через точки: (8,5) і (6,3).

    Відповідь

    1

    Вправа\(\PageIndex{27}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої через точки: (1,5) і (5,9).

    Відповідь

    1

    Вправа\(\PageIndex{28}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої через точки (−2, −3) та (−7,4).

    Відповідь

    \(\begin{array} {ll} {\text{We’ll call (-2, -3) point #1 and (-7,4) point #2.}} &{\left( \begin{array}{c}{x_{1}, y_{1}} \\ {-2,-3}\end{array}\right) \left( \begin{array}{c}{x_{2}, y_{2}} \\ {-7,4}\end{array}\right)} \\ {\text{Use the slope formula.}} &{m = \frac{y_{2}-y_{1}}{x_{2}-x_{1}}} \\ {\text{Substitute the values.}} &{} \\ {\text{y of the second point minus y of the first point}} &{m=\frac{4-(-3)}{x_{2}-x_{1}}} \\{\text{x of the second point minus x of the first point}} &{m = \frac{4-(-3)}{-7-(-2)}} \\{\text{Simplify the numerator and the denominator.}} &{m = \frac{7}{-5}} \\{\text{Simplify.}} &{m = -\frac{7}{5}} \end{array}\)

    Давайте перевіримо цей нахил на показаному графіку.

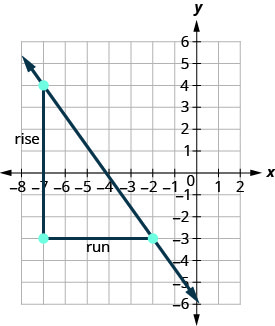
    На графіку показана координатна площина x y. Вісь X площини проходить від негативних 8 до 2, а вісь y площини проходить від негативних 6 до 5. Через точки (від'ємний 7, 4) і (від'ємний 2, негативний 3) проходить лінія, які нанесені і маркуються. Додаткова точка наноситься на (негативний 7, негативний 3). Три точки утворюють прямокутний трикутник, причому лінія від (негативний 7, 4) до (негативний 2, негативний 3) утворює гіпотенузу, а лінії від (негативний 7, 4) до (негативний 7, негативний 3) і від (негативний 7, негативний 3) до (негативний 2, негативний 3) утворюють катети. Нога від (негативний 7, 4) до (негативний 7, негативний 3) позначається як «підйом», а нога від (негативний 7, негативний 3) до (негативний 2, негативний 3) позначається як «бігти».

    \[\begin{aligned} m &=\frac{\text { rise }}{\text { run }} \\ m &=\frac{-7}{5} \\ m &=-\frac{7}{5} \end{aligned}\]

    Вправа\(\PageIndex{29}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої через точки: (−3,4) та (2, −1).

    Відповідь

    -1

    Вправа\(\PageIndex{30}\)

    Використовуйте формулу нахилу, щоб знайти нахил прямої через пару точок: (−2,6) та (−3, −4).

    Відповідь

    10

    Графік лінії з заданою точкою та нахилом

    До цих пір в цьому розділі ми графували лінії шляхом побудови точок, використовуючи перехоплення та розпізнаючи горизонтальні та вертикальні лінії.

    Ще один метод, який ми можемо використовувати для графіків ліній, називається метод точка-нахил. Ми будемо використовувати цей метод, коли дізнаємося одну точку і нахил лінії. Ми почнемо з побудови точки, а потім використаємо визначення нахилу, щоб намалювати графік лінії.

    Вправа\(\PageIndex{31}\)

    Графік лінії, що проходить через точку (1, −1), нахил якої дорівнює\(m = \frac{3}{4}\).

    Відповідь

    Ця таблиця складається з трьох стовпців і чотирьох рядків. Перший ряд говорить: «Крок 1. Побудуйте задану точку. Сюжет (1, негативний 1)». Праворуч - графік координатної площини x y. Вісь X площини проходить від негативного 1 до 7. Вісь Y площини проходить від негативних 3 до 4. Відзначається точка (0, від'ємна 1).Другий ряд говорить: «Крок 2. Використовуйте формулу нахилу m дорівнює підйому, розділеному на пробіг, щоб визначити підйом і пробіг». Підйом і біг - 3 і 4, тому м дорівнює 3, розділеному на 4.Третій ряд говорить «Крок 3. Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку». Починаємо з (1, негативний 1) і вважаємо підйом і біг. Вгору три одиниці і вправо 4 одиниці. На графіку праворуч нанесені додаткові дві точки: (1, 2), що на 3 одиниці вище (1, від'ємна 1), і (5, 2), що становить 3 одиниці вгору і 4 одиниці прямо від (1, від'ємна 1).Четвертий ряд говорить «Крок 4. З'єднайте точки лінією». На графіку праворуч проводиться лінія через точки (1, від'ємна 1) і (5, 2). Ця лінія також є гіпотенузою прямокутного трикутника, утвореного трьома точками, (1, негативним 1), (1, 2) і (5, 2).

    Вправа\(\PageIndex{32}\)

    Графік лінії, що проходить через точку (2, −2) з нахилом\(m = \frac{4}{3}\).

    Відповідь

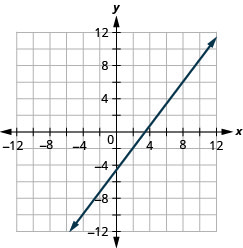
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (від'ємний 4, негативний 10) і (2, негативний 2) проходить лінія.

    Вправа\(\PageIndex{33}\)

    Графік лінії, що проходить через точку (−2,3) з нахилом\(m=\frac{1}{4}\).

    Відповідь

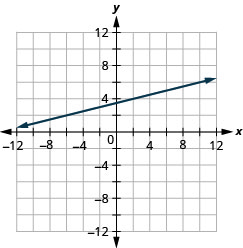
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Через точки (від'ємні 2, 3) і (10, 6) проходить лінія.

    ГРАФІК ЛІНІЇ ЗАДАНО ТОЧКУ І НАХИЛ.
    1. Побудуйте задану точку.
    2. Використовуйте формулу нахилу\(m=\frac{\text { rise }}{\text { rise }}\), щоб визначити підйом і пробіг.
    3. Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку.
    4. З'єднайте точки лінією.
    Вправа\(\PageIndex{34}\)

    Графік лінії з y -перехоплення 2, нахил якої дорівнює\(m=−\frac{2}{3}\).

    Відповідь

    Побудуйте задану точку, y -перехоплення, (0,2).

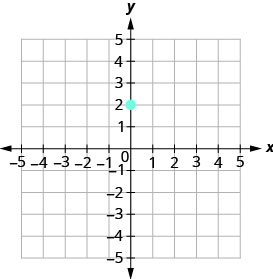
    Графік показує координатну площину x y. Осі x та y проходять від негативних 5 до 5. Відзначається точка (0, 2).

    \(\begin{array} {ll} {\text{Identify the rise and the run.}} &{m =-\frac{2}{3}} \\ {} &{\frac{\text { rise }}{\text { run }} =\frac{-2}{3} }\\ {}&{\text { rise } =-2} \\ {} &{\text { run } =3} \end{array}\)

    Підрахуйте підйом і біг. Відзначте другий пункт.

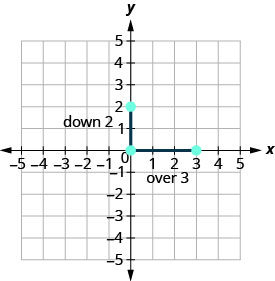
    Графік показує координатну площину x y. Осі x та y проходять від негативних 5 до 5. Точки (0, 2), (0, 0) та (3,0) нанесені та позначені. Рядок від (0, 2) до (0, 0) позначається «вниз 2», а рядок від (0, 0) до (3, 0) позначається «праворуч 3».

    З'єднайте дві точки лінією.

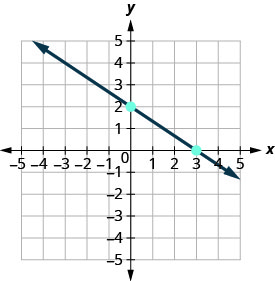
    Графік показує координатну площину x y. Осі x та y проходять від негативних 5 до 5. Через нанесені точки (0, 2) і (3,0) проходить лінія.

    Перевірити свою роботу можна, знайшовши третій пункт. Так як ухил є\(m=−\frac{2}{3}\), то його можна записати як\(m=\frac{2}{-3}\). Поверніться до (0,2) і відрахуйте підйом, 2 і пробіг, −3.

    Вправа\(\PageIndex{35}\)

    Графік лінії з y -перехопленням 4 і нахилом\(m=−\frac{5}{2}\).

    Відповідь

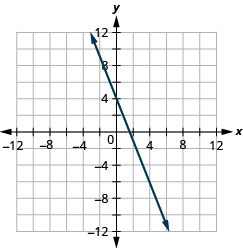
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Лінія перехоплює вісь y в (0, 4) і проходить через точку (4, негативна 6).

    Вправа\(\PageIndex{36}\)

    Графік лінії з x -перехопленням −3 та нахилом\(m=−\frac{3}{4}\).

    Відповідь

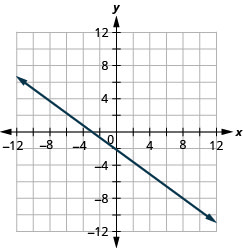
    Графік показує координатну площину x y. Осі x та y проходять від негативних 12 до 12. Лінія перехоплює вісь x в (негативний 3, 0) і проходить через точку (1, негативна 3).

    Вправа\(\PageIndex{37}\)

    Графік лінії, що проходить через точку (−1, −3), нахил якої дорівнює m=4.

    Відповідь

    Побудуйте задану точку.

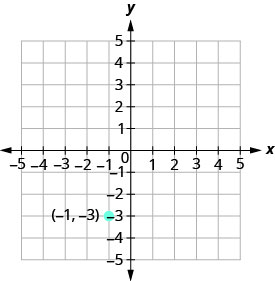
    Графік показує координатну площину x y. Осі x та y проходять від негативних 5 до 5. Крапка (негативна 1, негативна 3) наноситься і маркується.

    \(\begin{array} {ll} {\text{Identify the rise and the run.}} &{ \text{ m = 4}} \\ {\text{Write 4 as a fraction.}} &{\frac{\text {rise}}{\text {run}} =\frac{4}{1} }\\ {}&{\text {rise} =4\quad\text {run} =3} \end{array}\)

    Підрахуйте підйом і біжіть і відзначте другу точку.

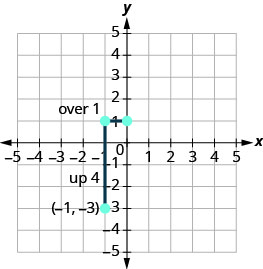
    На цьому малюнку показано, як побудувати графік лінії, що проходить через точку (негативна 1, негативна 3), нахил якої дорівнює 4. Насамперед необхідно визначити підйом і біг. Підйом дорівнює 4, а прогін 1. 4 ділиться на 1 дорівнює 4, тому нахил дорівнює 4. Далі вважаємо підйом і бігом і відзначаємо другу точку. Праворуч - графік координатної площини x y. Осі x та y проходять від негативних 5 до 5. Починаємо з наміченої точки (негативний 1, негативний 3) і вважаємо підйом, 4. Доходимо до точки негативної 1, 1, яку намічаємо. Потім відраховуємо пробіг з цієї точки, яка дорівнює 1. Доходимо до точки (0, 1), яка нанесена. Останній крок - з'єднати дві точки лінією. Проводимо лінію, яка проходить через точки (негативний 1, негативний 3) і (0, 1).

    З'єднайте дві точки лінією.

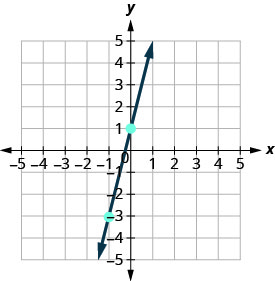
    Графік показує координатну площину x y. Осі x та y проходять від негативних 5 до 5. Через нанесені точки (-1, -3) і (1,0) проходить лінія.

    Перевірити свою роботу можна, знайшовши третій пункт. Оскільки нахил дорівнює m = 4, його можна записати як\(m = \frac{-4}{-1}\). Поверніться до (−1, −3) і відрахуйте підйом, −4 та пробіг, −1.

    Вправа\(\PageIndex{38}\)

    Графік лінії з точкою (−2,1) і нахилом m=3.

    Відповідь

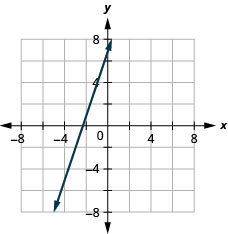
    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (від'ємні 2, 1) і (від'ємні 1, 4) проходить лінія.

    Вправа\(\PageIndex{39}\)

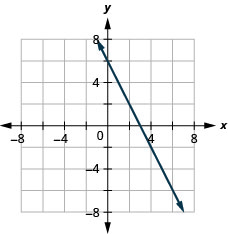
    Графік лінії з точкою (4, −2) і нахилом m=−2.

    Відповідь

    Графік показує координатну площину x y. Осі x та y проходять від негативних 7 до 7. Через точки (4, від'ємний 2) і (5, негативний 4) проходить лінія.

    Вирішіть програми нахилу

    На початку цього розділу ми сказали, що існує багато застосувань нахилу в реальному світі. Давайте розглянемо декілька зараз.

    Вправа\(\PageIndex{40}\)

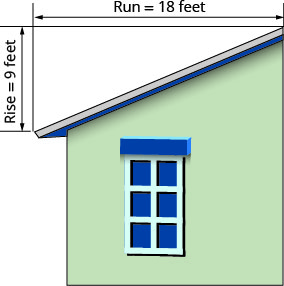
    «Крок» даху будівлі - це нахил даху. Знання поля важливо в кліматі, де є сильний снігопад. Якщо дах занадто рівна, вага снігу може стати причиною її обвалення. Який ухил покрівлі показаний?

    На цьому малюнку зображений будинок з похилим дахом. Дах на одній половині будівлі маркується «ухил даху». Існує відрізок лінії зі стрілками на кожному кінці вимірювання вертикальної довжини даху і позначений «підйом дорівнює 9 футів». Існує відрізок лінії зі стрілками на кожному кінці вимірювання горизонтальної довжини кореня і позначений «пробіг дорівнює 18 футів».

    Відповідь

    \(\begin{array}{ll}{\text { Use the slope formula. }} & {m=\frac{\text { rise }}{\text { rise }}} \\ {\text { Substitute the values for rise and run. }} & {m=\frac{9}{18}} \\ {\text { Simplify. }} & {m=\frac{1}{2}}\\ {\text{The slope of the roof is }\frac{1}{2}.} &{} \\ {} &{\text{The roof rises 1 foot for every 2 feet of}} \\ {} &{\text{horizontal run.}} \end{array}\)

    Вправа\(\PageIndex{41}\)

    Використовуйте Вправу\(\PageIndex{40}\), підставляючи підйом = 14 і біг = 24.

    Відповідь

    \(\frac{7}{12}\)

    Вправа\(\PageIndex{42}\)

    Використовуйте Вправу\(\PageIndex{40}\), підставляючи підйом = 15 і біг = 36.

    Відповідь

    \(\frac{5}{12}\)

    Вправа\(\PageIndex{43}\)

    Ви коли-небудь замислювалися над каналізаційними трубами, що йдуть з вашого будинку на вулицю? Вони повинні нахилятися вниз\(\frac{1}{4}\) дюйм на фут, щоб правильно стікати. Який необхідний ухил?

    Ця фігура являє собою прямокутний трикутник. Одна нога негативна одна чверть дюйма, а інша нога - одна нога.

    Відповідь

    \(\begin{array} {ll} {\text{Use the slope formula.}} &{m=\frac{\text { rise }}{\text { run }}} \\ {} &{m=\frac{-\frac{1}{4} \mathrm{inch}}{1 \text { foot }}}\\ {}&{m=\frac{-\frac{1}{4} \text { inch }}{12 \text { inches }}} \\ {\text{Simplify.}} &{m=-\frac{1}{48}} \\{} &{\text{The slope of the pipe is }-\frac{1}{48}} \end{array}\)

    Труба падає 1 дюйм на кожні 48 дюймів горизонтального ходу.

    Вправа\(\PageIndex{44}\)

    Знайдіть нахил труби, яка нахиляється вниз\(\frac{1}{3}\) дюйм на фут.

    Відповідь

    \(-\frac{1}{36}\)

    Вправа\(\PageIndex{45}\)

    Знайдіть нахил труби, яка нахиляється вниз\(\frac{3}{4}\) дюйм на двір.

    Відповідь

    \(-\frac{1}{48}\)

    Отримайте доступ до цих онлайн-ресурсів для додаткових інструкцій та практики з розумінням нахилу лінії.

    Ключові концепції

    • Знайдіть нахил прямої з її графіка за допомогою\(m=\frac{\text { rise }}{\text { run }}\)
      1. Знайдіть дві точки на лінії, координати яких є цілими числами.
      2. Починаючи з точки зліва, накидайте прямокутний трикутник, що йде від першої точки до другої точки.
      3. Підрахуйте підйом і біг на ніжках трикутника.
      4. Візьміть співвідношення підйому до бігу, щоб знайти схил.
    • Графік лінії з заданою точкою та нахилом
      1. Побудуйте задану точку.
      2. Використовуйте формулу нахилу\(m=\frac{\text { rise }}{\text { run }}\), щоб визначити підйом і пробіг.
      3. Починаючи з заданої точки, відраховуйте підйом і біжіть, щоб відзначити другу точку.
      4. З'єднайте точки лінією.
    • Нахил горизонтальної лінії
      • Нахил горизонтальної лінії, y=b, дорівнює 0.
    • Ухил вертикальної лінії
      • Нахил вертикальної лінії, x=a, не визначено