Skip to main content
LibreTexts - Ukrayinska

4.7: Графіки лінійних нерівностей

  1. Last updated
  2. Save as PDF
  • Page ID
    58825

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Перевірка розв'язків нерівності в двох змінних
    • Визнати зв'язок між розв'язками нерівності та її графіком
    • Лінійні нерівності графа
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Вирішити:\(4x+3>23.\)
      Якщо ви пропустили цю проблему, перегляньте Вправу 2.7.22.
    2. Перекласти з алгебри на англійську:\(x<5.\)
      Якщо ви пропустили цю проблему, перегляньте Вправу 1.3.1.
    3. Оцініть,\(3x−2y\) коли\(x=1, \, y=−2.\)
      Якщо ви пропустили цю проблему, перегляньте Вправу 1.5.28.

    Перевірка рішень нерівності в двох змінних

    Ми навчилися вирішувати нерівності в одній змінній. Тепер ми розглянемо нерівності в двох змінних. Нерівності в двох змінних мають багато застосувань. Наприклад, якщо ви керуєте бізнесом, ви хотіли б, щоб ваш дохід був більшим за ваші витрати, щоб ваш бізнес отримував прибуток.

    ЛІНІЙНА НЕРІВ

    Лінійна нерівність - це нерівність, яку можна записати в одну з наступних форм:

    \[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C \nonumber\]

    де\(A\) і не\(B\) обидва нульові.

    Ви пам'ятаєте, що нерівність з однією змінною мала багато рішень? Рішення нерівності\(x>3\) є будь-яке число більше, ніж\(3\). Ми показали це на числовому рядку затінення в числовому рядку праворуч від\(3\), і покласти відкриті дужки на\(3\). Див\(\PageIndex{1}\). Малюнок.

    На малюнку показана числова лінія, що простягається від негативних 5 до 5. Дужка показана на додатному 3, а стрілка розширюється від позитивної 3 до позитивної нескінченності.
    Малюнок\(\PageIndex{1}\)

    Аналогічно нерівності в двох змінних мають багато рішень. \( (x, y)\)Будь-яка впорядкована пара, яка робить нерівність істинною, коли ми підставляємо значення, є рішенням нерівності.

    Розв'язок ЛІНІЙНОЇ НЕРІВНОСТІ

    \( (x, y)\)Впорядкована пара - це рішення лінійної нерівності, якщо нерівність істинна, коли ми підставляємо значення\(x\) і\(y\).

    Вправа\(\PageIndex{1}\)

    Визначте, чи є кожна впорядкована пара розв'язком нерівності\(y>x+4\):

    1. \((0,0)\)
    2. \((1,6)\)
    3. \((2,6)\)
    4. \((−5,−15)\)
    5. \((−8,12)\)
    Відповідь
    1.
    \((0,0)\) .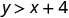
    . .
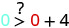
    Спростити. .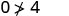
    Отже,\((0,0)\) це не рішення для\(y>x+4\).
    2.
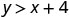
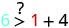
    \((1,6)\) .
    . .
    Спростити. .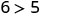
    Отже,\((1,6)\) це рішення для\(y>x+4\).
    3.
    \((2,6)\) .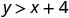
    . .
    Спростити. .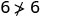
    Отже,\((2,6)\) це не рішення для\(y>x+4\).
    4.
    \((−5,−15)\) .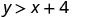
    . .
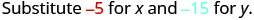
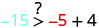
    Спростити. .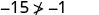
    Отже,\((−5,−15)\) це не рішення для\(y>x+4\).
    5.
    (−8,12) .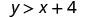
    . .
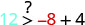
    Спростити. .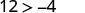
    Отже,\((−8,12)\) це рішення для\(y>x+4\).
    Вправа\(\PageIndex{2}\)

    Визначте, чи є кожна впорядкована пара розв'язком нерівності\(y>x−3\):

    1. \((0,0)\)
    2. \((4,9)\)
    3. \((−2,1)\)
    4. \((−5,−3)\)
    5. \((5,1)\)
    Відповідь
    1. так
    2. так
    3. так
    4. так
    5. ні
    Вправа\(\PageIndex{3}\)

    Визначте, чи є кожна впорядкована пара розв'язком нерівності\(y<x+1\):

    1. \((0,0)\)
    2. \((8,6)\)
    3. \((−2,−1)\)
    4. \((3,4)\)
    5. \((−1,−4)\)
    Відповідь
    1. так
    2. так
    3. ні
    4. ні
    5. так

    Визнати зв'язок між розв'язками нерівності та її графіком

    Тепер ми розглянемо, як розв'язки нерівності співвідносяться з його графіком.

    Давайте\(\PageIndex{1}\) знову подумаємо над числовим рядком на малюнку. Точка\(x=3\) розділила цю цифрову лінію на дві частини. На одній стороні\(3\) знаходяться всі числа менше, ніж\(3\). На іншій стороні\(3\) всі цифри більше, ніж\(3\). Див\(\PageIndex{2}\). Малюнок.

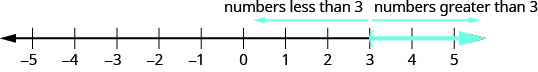
    На малюнку показана числова лінія, що простягається від негативних 5 до 5. Дужка показана на додатному 3, а стрілка розширюється від позитивної 3 до позитивної нескінченності. Стрілка над цифровою лінією простягається від 3 і вказує вліво. Він позначений як «цифри менше 3». Стрілка над цифровою лінією простягається від 3 і вказує вправо. Він позначений як «цифри більше 3».
    Малюнок\(\PageIndex{2}\)

    Рішення\(x>3\) - це затінена частина числового рядка праворуч від\(x=3\).

    Аналогічно лінія\(y=x+4\) розділяє площину на дві області. З одного боку лінії розташовані точки с\(y<x+4\). На іншій стороні лінії розташовані точки с\(y>x+4\). Називаємо лінію\(y=x+4\) лінією кордону.

    МЕЖОВА ЛІНІЯ

    Лінія з рівнянням\(Ax+By=C\) є граничною лінією, яка відокремлює область де\(Ax+By>C\) від області де\(Ax+By<C\).

    Для нерівності в одній змінній кінцева точка показана дужками або дужкою залежно від того, чи включено aa до розв'язку:

    На малюнку показані дві числові лінії. Числовий рядок ліворуч позначено x меншим за a. У цифровому рядку буде показано дужку біля a та стрілку, яка вказує ліворуч. Числовий рядок праворуч позначається з позначкою x менше або дорівнює a. У цифровому рядку показано дужку a та стрілку, яка вказує ліворуч.

    Аналогічно, для нерівності у двох змінних межа показана суцільною або пунктирною лінією, щоб вказати, чи включена лінія до розв'язку. Це підсумовано в табл\(\PageIndex{1}\).

    \(Ax+By<C\) \(Ax+By\leq C\)
    \(Ax+By>C\) \(Ax+By\geq C\)
    Гранична лінія не включається до розв'язку. У розв'язку включається межова лінія.
    Лінія кордону штрихова. Гранична лінія суцільна.
    Таблиця\(\PageIndex{1}\)

    Тепер давайте поглянемо на те, що ми знайшли в Вправи\(\PageIndex{1}\). Ми почнемо з графіка лінії\(y=x+4\), а потім ми побудуємо п'ять точок, які ми перевірили. Див\(\PageIndex{3}\). Малюнок.

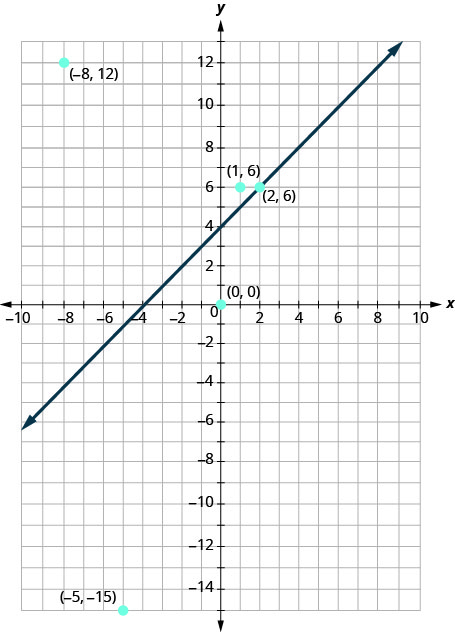
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює х плюс 4 нанесена у вигляді стрілки, що тягнеться знизу ліворуч до верхнього правого. Наступні точки нанесені та позначені (негативні 8, 12), (1, 6), (2, 6), (0, 0), і (негативні 5, негативні 15).
    Малюнок\(\PageIndex{3}\)

    У Вправи\(\PageIndex{1}\) ми виявили, що деякі пункти були рішеннями нерівності,\(y>x+4\) а деякі - ні.

    Які з точок, які ми побудували, є розв'язками нерівності\(y>x+4\)? Точки\((1,6)\) і\((−8,12)\) є розв'язками нерівності\(y>x+4\). Зверніть увагу, що вони обидва знаходяться на одній стороні лінії кордону\(y=x+4\).

    Дві точки\((0,0)\) і\((−5,−15)\) знаходяться на іншій стороні граничної лінії\(y=x+4\), і вони не є розв'язками нерівності\(y>x+4\). Для цих двох пунктів,\(y<x+4\).

    А як щодо суті\((2,6)\)? Тому що\(6=2+4\), точка - це рішення рівняння\(y=x+4\). Таким чином, точка\((2,6)\) знаходиться на лінії кордону.

    Візьмемо ще одну точку на лівій стороні лінії кордону і перевіримо, чи є це розв'язком нерівності\(y>x+4\). Точка\((0,10)\) явно виглядає ліворуч від лінії кордону, чи не так? Це рішення нерівності?

    \[\begin{array}{l}{y>x+4} \\ {10\stackrel{?}{>}0+4} \\ {10>4} &{\text{So, }(0,10)\text{ is a solution to }y>x+4.}\end{array}\]

    Будь-яка точка, яку ви виберете на лівій стороні лінії кордону, є розв'язком нерівності\(y>x+4\). Всі точки зліва - це рішення.

    Аналогічно, всі точки на правій стороні лінії кордону, сторона з\((0,0)\) і\((−5,−15)\), не є розв'язками\(y>x+4\). Див\(\PageIndex{4}\). Малюнок.

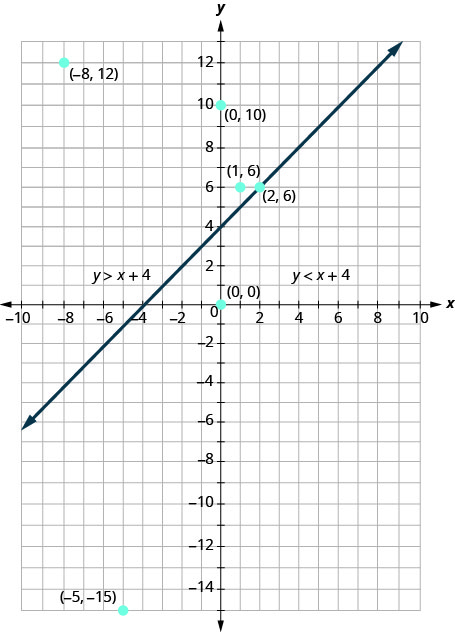
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює х плюс 4 будується у вигляді стрілки, що тягнеться знизу ліворуч до верхнього правого. Наступні точки нанесені та позначені (негативні 8, 12), (1, 6), (2, 6), (0, 0), і (негативні 5, негативні 15). У верхньому лівому куті лінії знаходиться нерівність y більша за x плюс 4. Праворуч від лінії знаходиться нерівність y менше x плюс 4.
    Малюнок\(\PageIndex{4}\)

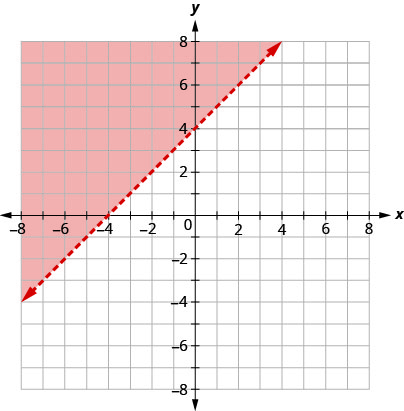
    Графік нерівності\(y>x+4\) показаний на малюнку\(\PageIndex{5}\) нижче. Лінія\(y=x+4\) ділить площину на дві області. Затінена сторона показує рішення нерівності\(y>x+4\).

    Точки на граничній лінії, ті де\(y=x+4\), не є розв'язками нерівності\(y>x+4\), тому сама лінія не є частиною розв'язку. Ми показуємо, що зробивши лінію пунктирною, а не суцільною.

    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює х плюс 4 нанесена як пунктирна стрілка, що тягнеться знизу ліворуч до верхнього правого. Координатна площина у верхній лівій частині лінії затінюється.
    Малюнок\(\PageIndex{5}\): Графік нерівності y>x+4.
    Вправа\(\PageIndex{4}\)

    Лінія кордону показана є\(y=2x−1\). Запишіть нерівність, показану графіком.

    Відповідь

    Лінія\(y=2x−1\) - межа. На одній стороні лінії знаходяться точки з,\(y>2x−1\) а з іншого боку лінії - точки с\(y<2x−1\).

    Давайте перевіримо точку\((0,0)\) і подивимося, яка нерівність описує її сторону межової лінії.

    При\((0,0)\), яке нерівність вірно:

    \[\begin{array}{ll}{y>2 x-1} & {\text { or }} & {y<2 x-1 ?} \\ {y>2 x-1} && {y<2 x-1} \\ {0>2 \cdot 0-1} && {0<2 \cdot 0-1} \\ {0>-1 \text { True }} && {0<-1 \text { False }}\end{array}\]

    Оскільки\(y>2x−1\) це правда, сторона лінії з\((0,0)\), є рішенням. Затінена область показує розв'язання нерівності\(y>2x−1\).

    Оскільки межова лінія зображена суцільною лінією, нерівність включає знак рівності.

    Графік показує нерівність\(y\geq 2x−1\).

    Ми могли б використовувати будь-яку точку як контрольну точку, за умови, що вона не знаходиться на лінії. Чому ми вибрали\((0,0)\)? Тому що це найпростіше оцінити. Можливо, ви захочете вибрати точку на іншій стороні лінії кордону і перевірити це\(y<2x−1\).

    Вправа\(\PageIndex{5}\)

    Запишіть нерівність, показану графіком, з граничною лінією\(y=−2x+3\).

    Відповідь

    \(y\geq −2x+3\)

    Вправа\(\PageIndex{6}\)

    Запишіть нерівність, показану графіком, з граничною лінією\(y=\frac{1}{2}x−4\).

    Відповідь

    \(y \leq \frac{1}{2}x - 4\)

    Вправа\(\PageIndex{7}\)

    Лінія кордону показана є\(2x+3y=6\). Запишіть нерівність, показану графіком.

    Відповідь

    Лінія\(2x+3y=6\) - межа. На одній стороні лінії знаходяться точки з,\(2x+3y>6\) а з іншого боку лінії - точки с\(2x+3y<6\).

    Давайте перевіримо точку\((0,0)\) і подивимося, яка нерівність описує її сторону межової лінії.

    При\((0,0)\), яке нерівність вірно:

    \[\begin{array}{rr}{2 x+3 y>6} && {\text { or } \quad 2 x+3 y<6 ?} \\ {2 x+3 y>6} && {2 x+3 y<6} \\ {2(0)+3(0)>6} & & {2(0)+3(0)<6} \\ {0} >6 & {\text { False }} & {0<6}&{ \text { True }}\end{array}\]

    Так що сторона з\((0,0)\) є стороною де\(2x+3y<6\).

    (Можливо, ви захочете вибрати точку на іншій стороні лінії кордону і перевірити це\(2x+3y>6\).)

    Оскільки межова лінія графічна як пунктирна лінія, нерівність не включає знак рівності.

    На графіку показано розв'язання нерівності\(2x+3y<6\).

    Вправа\(\PageIndex{8}\)

    Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією\(x−4y=8\).

    Відповідь

    \(x-4 y \leq 8\)

    Вправа\(\PageIndex{9}\)

    Запишіть нерівність, показану затіненою областю, на графіку з граничною лінією\(3x−y=6\).

    Відповідь

    \(3 x-y \leq 6\)

    Лінійні нерівності графа

    Тепер, ми готові зібрати все це разом, щоб графік лінійних нерівностей.

    Вправа\(\PageIndex{10}\): How to Graph Linear Inequalities

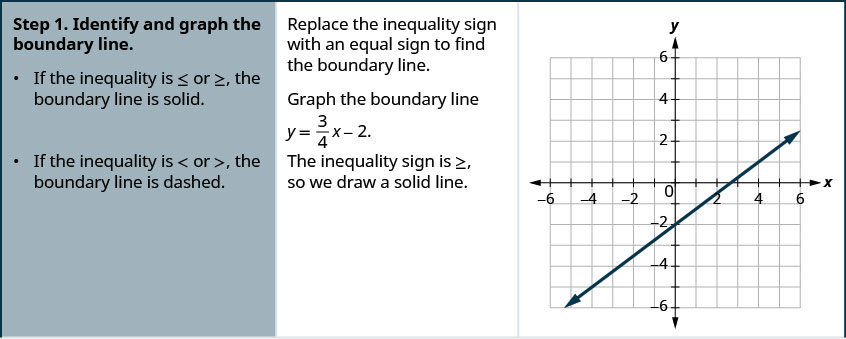
    Графік лінійної нерівності\(y \geq \frac{3}{4} x-2\).

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і три рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить математику. У верхньому рядку таблиці перша клітинка зліва говорить: «Крок 1. Визначте та графуйте лінію кордону. Якщо нерівність менше або дорівнює або більше або дорівнює або дорівнює, межова лінія є суцільною. Якщо нерівність менше або більше, межова лінія штриховою. Текст у другій клітинці говорить: «Замініть знак нерівності на знак рівності, щоб знайти межу. Графік межової лінії y дорівнює трьом четвертим x мінус 2. Знак нерівності більше або дорівнює, тому проводимо суцільну лінію. Третя комірка містить графік прямої три чверті х мінус 2 на координатній площині.У другому рядку таблиці перша осередок говорить: «Крок 2. Перевірте точку, яка не знаходиться на лінії кордону. Це рішення нерівності? У другій осередку в інструкції написано: «Будемо тестувати (0, 0). Це рішення нерівності?» Третя комірка запитує: At (0, 0), y більше або дорівнює трьом четвертим x мінус 2? Нижче наведено нерівність 0 більше або дорівнює трьом четвертам 0 мінус 2, зі знаком питання над символом нерівності. Нижче наведено нерівність 0 більше або дорівнює від'ємному 2. 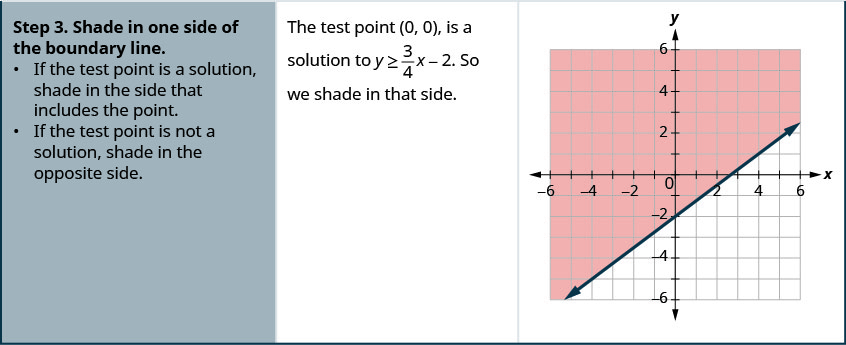Нижче це: «Отже (0, 0) - це рішення.У третьому рядку таблиці перша осередок говорить: «Крок 3. Заштрихуйте в одну сторону лінії кордону. Якщо контрольною точкою є розчин, затінюйте в ту сторону, яка включає точку. Якщо контрольна точка не є розчином, розтушуйте в протилежну сторону. У другій комірці інструкції говорять: Тестова точка (0, 0) - це рішення y більше або дорівнює трьом чвертям х мінус 2. Тож ми затінюємо в ту сторону». У третій комірці знаходиться графік прямої три чверті х мінус 2 на координатній площині з областю над лінією затіненої.

    Вправа\(\PageIndex{11}\)

    Графік лінійної нерівності\(y \geq \frac{5}{2} x-4\).

    Відповідь

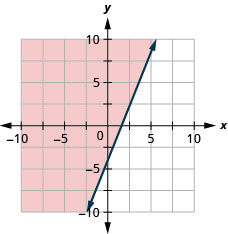
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює п'ять половин х мінус 4 будується як суцільна стрілка, що тягнеться знизу ліворуч до верхнього праворуч. Область над лінією затінюється.

    Вправа\(\PageIndex{12}\)

    Графік лінійної нерівності\(y<\frac{2}{3} x-5\).

    Відповідь

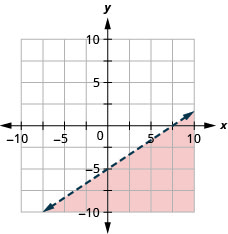
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює двом третинам х мінус 5 наноситься як пунктирна стрілка, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінюється.

    Кроки, які ми робимо для графіку лінійної нерівності, підсумовуються тут.

    ГРАФІК A ЛІНІЙНА НЕРІВНІСТЬ.
    1. Визначте та графуйте лінію кордону.
      • Якщо нерівність дорівнює\(≤\) або\(≥\), межова лінія суцільна.
      • Якщо нерівність дорівнює\(<\) або\(>\), межова лінія буде пунктирною.
    2. Перевірте точку, яка не знаходиться на лінії кордону. Це рішення нерівності?
    3. Заштрихуйте в одну сторону лінії кордону.
      • Якщо контрольною точкою є розчин, затінюйте в ту сторону, яка включає точку.
      • Якщо контрольна точка не є розчином, розтушуйте в протилежну сторону.
    Вправа\(\PageIndex{13}\)

    Графік лінійної нерівності\(x−2y<5\).

    Відповідь

    Спочатку графуємо лінію кордону\(x−2y=5\). Нерівність полягає в\(<\) тому, що ми проводимо пунктирну лінію.

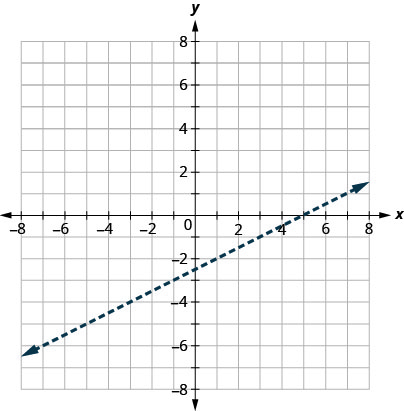
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія х мінус 2 у дорівнює 5 наноситься як пунктирна стрілка, що тягнеться знизу ліворуч до верхнього праворуч.

    Потім перевіряємо точку. Ми будемо використовувати\((0,0)\) знову, тому що це легко оцінити, і це не на лінії кордону.

    Чи\((0,0)\) є рішенням\(x−2y<5\)?

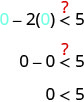
    На малюнку показано нерівність 0 мінус 2 рази 0 в дужках менше 5, зі знаком питання над символом нерівності. Наступний рядок показує 0 мінус 0 менше 5, зі знаком питання над символом нерівності. У третьому рядку показано 0 менше 5.

    Точка\((0,0)\) є рішенням\(x−2y<5\), тому ми затінюємо в цій стороні лінії кордону.

    Вправа\(\PageIndex{14}\)

    Графік лінійної нерівності\(2x−3y\leq 6\).

    Відповідь

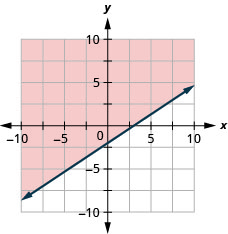
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 2 х мінус 3 y дорівнює 6 будується як суцільна стрілка, що тягнеться знизу ліворуч до верхнього праворуч. Область над лінією затінюється.

    Вправа\(\PageIndex{15}\)

    Графік лінійної нерівності\(2x−y>3\).

    Відповідь

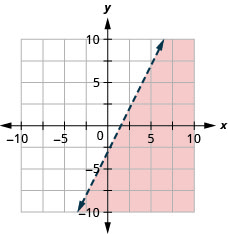
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія 2 х мінус у дорівнює 3 наноситься як пунктирна стрілка, що тягнеться знизу ліворуч до верхнього праворуч. Область нижче лінії затінюється.

    Що робити, якщо межа проходить через початок? Тоді ми не зможемо використовувати\((0,0)\) як контрольну точку. Немає проблем - ми просто виберемо якусь іншу точку, яка не знаходиться на лінії кордону.

    Вправа\(\PageIndex{16}\)

    Графік лінійної нерівності\(y\leq −4x\).

    Відповідь

    Спочатку графуємо лінію кордону\(y=−4x\). Він знаходиться у формі нахилу—перехоплення, з\(m=−4\) і\(b=0\). Нерівність полягає в\(≤\) тому, що ми проводимо суцільну лінію.

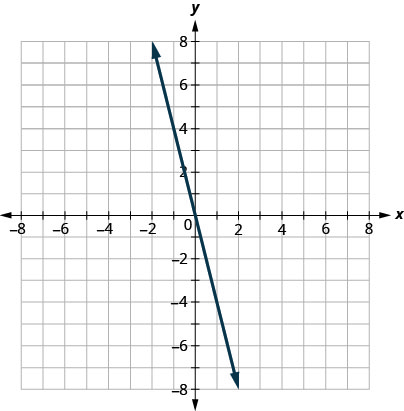
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія s y дорівнює негативному 4 х будується як суцільна стрілка, що тягнеться від верхнього лівого краю до нижнього правого.

    Тепер нам потрібна контрольна точка. Ми бачимо, що точка\((1,0)\) знаходиться не на граничній лінії.

    Чи\((1,0)\) є рішенням\(y≤−4x\)?

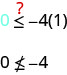
    На малюнку показано, що 0 менше або дорівнює негативному 4 рази 1 в дужках, зі знаком питання над символом нерівності. Наступний рядок показує 0 не менше або дорівнює від'ємному 4.

    Точка не\((1,0)\) є рішенням\(y≤−4x\), тому затінюємо в протилежну сторону лінії кордону. Див\(\PageIndex{6}\). Малюнок.

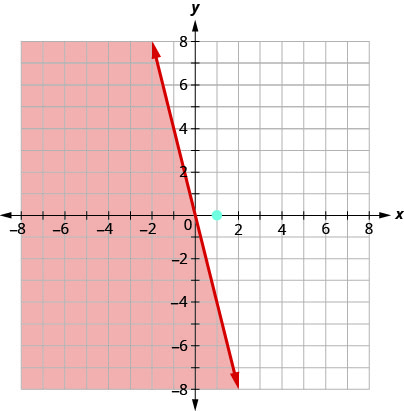
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 4 х будується як суцільна стрілка, що тягнеться від верхнього лівого краю до нижнього правого. Точка (1, 0) наноситься, але не позначена. Область зліва від лінії затінюється.
    Малюнок\(\PageIndex{6}\)
    Вправа\(\PageIndex{17}\)

    Графік лінійної нерівності\(y>−3x\).

    Відповідь

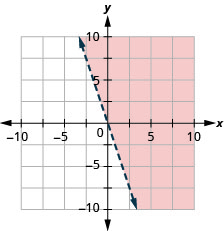
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 3 х наноситься як пунктирна стрілка, що тягнеться від верхнього лівого краю до нижнього правого. Область праворуч від лінії затінюється.

    Вправа\(\PageIndex{18}\)

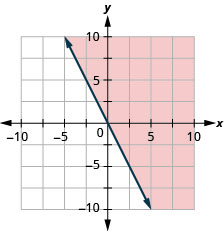
    Графік лінійної нерівності\(y\geq −2x\).

    Відповідь

    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 2 х будується як суцільна стрілка, що тягнеться від верхнього лівого краю до нижнього правого. Область праворуч від лінії затінюється.

    Деякі лінійні нерівності мають лише одну змінну. Вони можуть мати\(x\) але ні\(y\), або\(y\) але ні\(x\). У цих випадках лінія кордону буде або вертикальною, або горизонтальною лінією. Ви пам'ятаєте?

    \(\begin{array}{ll}{x=a} & {\text { vertical line }} \\ {y=b} & {\text { horizontal line }}\end{array}\)

    Вправа\(\PageIndex{19}\)

    Графік лінійної нерівності\(y>3\).

    Відповідь

    Спочатку графуємо лінію кордону\(y=3\). Вона являє собою горизонтальну лінію. Нерівність полягає в\(>\) тому, що ми проводимо пунктирну лінію.

    Тестуємо точку\((0,0)\).

    \[y>3 \\ 0\not>3\]

    \((0,0)\)це не рішення\(y>3\).

    Так затінюємо ту сторону, яка не включає\((0,0)\).

    Вправа\(\PageIndex{20}\)

    Графік лінійної нерівності\(y<5\).

    Відповідь

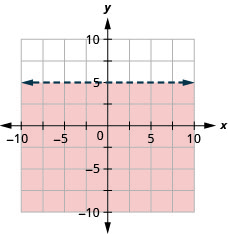
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює 5 наноситься як пунктирна стрілка горизонтально по всій площині. Область над лінією затінюється.

    Вправа\(\PageIndex{21}\)

    Графік лінійної нерівності\(y \leq-1\).

    Відповідь

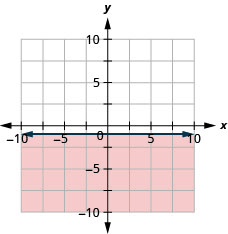
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 10 до 10. Лінія y дорівнює негативному 1 наноситься як пунктирна стрілка горизонтально по всій площині. Область нижче лінії затінюється.

    Ключові концепції

    • Графік лінійної нерівності
      1. Визначте та графуйте лінію кордону.
        Якщо нерівність дорівнює\(≤\) або\(≥\), межова лінія суцільна.
        Якщо нерівність дорівнює\(<\) або\(>\), межова лінія буде пунктирною.
      2. Перевірте точку, яка не знаходиться на лінії кордону. Це рішення нерівності?
      3. Заштрихуйте в одну сторону лінії кордону.
        Якщо контрольною точкою є розчин, затінюйте в ту сторону, яка включає точку.
        Якщо контрольна точка не є розчином, розтушуйте в протилежну сторону.

    Глосарій

    межова лінія
    Лінія з рівнянням\(A x+B y=C\), що відокремлює область де\(A x+B y>C\) від області де\(A x+B y<C\).
    лінійна нерівність
    Нерівність, яка може бути записана в одній з наступних форм:

    \[A x+B y>C \quad A x+B y \geq C \quad A x+B y<C \quad A x+B y \leq C\]

    де\(A\) і не\(B\) обидва нульові.
    розв'язок лінійної нерівності
    \((x,\,y)\)Впорядкована пара - це рішення лінійної нерівності, нерівність істинна, коли ми підставляємо значення\(x\) і\(y\).