Skip to main content
LibreTexts - Ukrayinska

4.6: Знайдіть рівняння прямої

  1. Last updated
  2. Save as PDF
  • Page ID
    58795

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Знайти рівняння прямої з заданим нахилом і y-перехопленням
    • Знайти рівняння прямої, заданої нахилом і точкою
    • Знайти рівняння прямої заданої двох точок
    • Знайти рівняння прямої, паралельної заданій прямій
    • Знайти рівняння прямої, перпендикулярної заданому рядку
    Примітка

    Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

    1. Вирішити:\(\frac{2}{3} = \frac{x}{5}\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 2.2.4.
    2. Спростити:\(−\frac{2}{5}(x−15)\).
      Якщо ви пропустили цю проблему, перегляньте Вправа 1.10.34.

    Як інтернет-магазини знають, що «вам також може сподобатися» конкретний пункт на основі того, що ви тільки що замовили? Як економісти можуть знати, як підвищення мінімальної заробітної плати вплине на рівень безробіття? Як медичні дослідники створюють препарати для націлювання на ракові клітини? Як дорожні інженери можуть передбачити вплив на ваш час поїздки підвищення або зниження цін на газ? Це все математика.

    Ви перебуваєте в захоплюючій точці своєї математичної подорожі, оскільки математика, яку ви вивчаєте, має цікаві програми в реальному світі.

    Фізичні науки, соціальні науки та діловий світ сповнені ситуацій, які можуть бути змодельовані за допомогою лінійних рівнянь, що стосуються двох змінних. Дані збираються та графуються. Якщо точки даних утворюють пряму лінію, рівняння цієї лінії може бути використано для прогнозування значення однієї змінної на основі значення іншої змінної.

    Щоб створити математичну модель лінійного співвідношення між двома змінними, ми повинні вміти знаходити рівняння прямої. У цьому розділі ми розглянемо кілька способів написання рівняння прямої. Конкретний метод, який ми використовуємо, буде визначатися тим, яку інформацію нам дають.

    Знайти рівняння прямої з заданим нахилом та y -перехопленням

    Ми можемо легко визначити нахил і перехоплення прямої, якщо рівняння було записано у формі нахилу - перехоплення, y = mx+b Тепер ми зробимо зворотне - ми почнемо з нахилу і y -перехоплення і використаємо їх, щоб знайти рівняння прямої.

    Вправа\(\PageIndex{1}\)

    Знайти рівняння прямої з нахилом −7 та y -перехопленням (0, −1).

    Відповідь

    Оскільки нам задано нахил і y -перехоплення лінії, ми можемо підставити потрібні значення у форму нахилу—перехоплення, y=mx+b.

    Назвіть ухил. .
    Назвіть y -перехоплення. .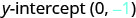
    Підставляємо значення у y = mx+b. .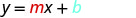
      .
      .
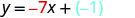
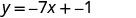
    Вправа\(\PageIndex{2}\)

    Знайти рівняння прямої з нахилом\(\frac{2}{5}\) і y -перехопленням (0,4).

    Відповідь

    \(y = \frac{2}{5}x + 4\)

    Вправа\(\PageIndex{3}\)

    Знайти рівняння прямої з нахилом −1 та y -перехопленням (0, −3).

    Відповідь

    \(y=−x−3\)

    Іноді, нахил і перехоплення потрібно визначати з графіка.

    Вправа\(\PageIndex{4}\)

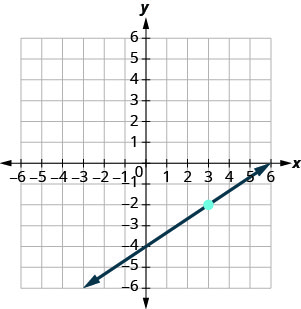
    Знайдіть рівняння показаної прямої.

    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія перехоплює вісь y в (0, негативний 4), проходить через нанесену точку (3, негативну 2) і перехоплює вісь x в (4, 0).

    Відповідь

    Нам потрібно знайти нахил і y -перехоплення прямої з графіка, щоб ми могли підставити потрібні значення у форму нахилу - перехоплення, y=mx+by=mx+b.

    Щоб знайти нахил, вибираємо дві точки на графіку.

    Перехоплення y дорівнює (0, −4), а графік проходить через (3, −2).

    Знайдіть нахил, вважаючи підйом і біг. .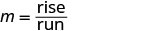
      .
    Знайдіть y -перехоплення. .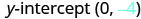
    Підставляємо значення у y = mx+b. .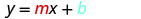
      .
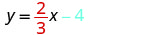
    Вправа\(\PageIndex{5}\)

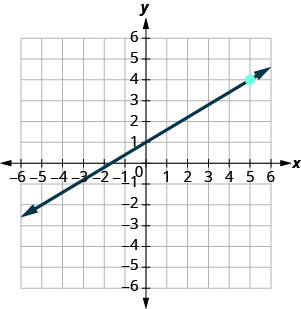
    Знайдіть рівняння прямої, наведеної на графіку.

    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія перехоплює вісь x в (негативний 2, 0), перехоплює вісь y в (0, 1) і проходить через нанесену точку (5, 4).

    Відповідь

    \(y=\frac{3}{5}x+1\)

    Вправа\(\PageIndex{6}\)

    Знайдіть рівняння прямої, наведеної на графіку.

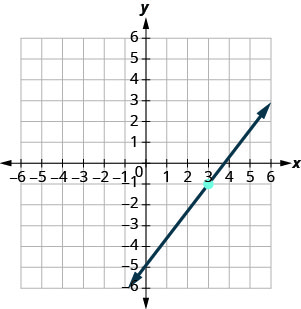
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія перехоплює вісь y в (0, негативний 5), проходить через нанесену точку (3, негативну 1) і перехоплює вісь x в (15 четвертих, 0).

    Відповідь

    \(y=\frac{4}{3}x−5\)

    Знайти рівняння прямої з заданим нахилом і точкою

    Пошук рівняння прямої за допомогою форми нахилу - перехоплення рівняння добре працює, коли вам задано нахил і y -перехоплення або коли ви читаєте їх з графіка. Але що відбувається, коли у вас є інша точка замість y -перехоплення?

    Ми будемо використовувати формулу нахилу, щоб отримати іншу форму рівняння прямої. Припустимо, у нас є лінія, яка має нахил мм і яка містить якусь конкретну точку\((x_{1}, y_{1})\) та якусь іншу точку, яку ми просто назвемо (x, y). Ми можемо написати нахил цієї лінії, а потім змінити його на іншу форму.

    \(\begin{array} {lrll}&m &=\frac{y-y_{1}}{x-x_{1}} \\ \text{Multiply both sides of the equation by }x−x_{1}.&m\left(x-x_{1}\right) &=\left(\frac{y-y_{1}}{x-x_{1}}\right)\left(x-x_{1}\right) \\ \text{Simplify.}&m\left(x-x_{1}\right) &=y-y_{1} \\ \text{Rewrite the equation with the y terms on the left.} &y-y_{1} &=m\left(x-x_{1}\right) \end{array}\)

    Цей формат називається точка-нахил форми рівняння прямої.

    ТОЧКА—НАХИЛ ФОРМА РІВНЯННЯ ПРЯМОЇ

    Точка-нахил форми рівняння прямої з нахилом мм і містить точку\((x_{1}, y_{1})\)

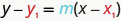
    Немає альтернативного тексту

    Ми можемо використовувати точку - нахил форми рівняння, щоб знайти рівняння прямої, коли нам задано нахил і одну точку. Потім ми перепишемо рівняння у формі нахилу - перехоплення. Більшість застосувань лінійних рівнянь використовують форму нахилу—перехоплення.

    Вправа\(\PageIndex{7}\): Find an Equation of a Line Given the Slope and a Point

    Знайдіть рівняння прямої з нахилом\(m=\frac{2}{5}\), що містить точку (10,3). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить математику. У першому рядку таблиці перша комірка зліва говорить: «Крок 1. Визначте схил». Текст у другій клітинці говорить: «Нахил заданий». Третя комірка містить нахил прямої, визначеної як m дорівнює 2 п'ятих.
    У другому рядку перша клітинка говорить: «Крок 2. Визначте точку». Друга клітинка говорить: «Точка дана». Третя клітинка містить впорядковану пару (10, 3). Верхній індекс x нижнього індексу 1 пишеться більше 10, а верхній індекс y нижнього індексу 1 пишеться над 3.
    У третьому ряду перша клітинка говорить: «Крок 3. Підставляйте значення у форму точки-нахилу, y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках.» Верхній рядок другої клітинки залишаємо порожньою. Третя комірка містить форму точкового нахилу, записану знову: y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках. Нижче наведено форму точки-нахилу з 10 замінені на x індекс 1, 3 замінені на y індекс 1, і 2 п'яті замінені на m: y мінус 3 дорівнює 2 п'ятих разів x мінус 10 в дужках. Один рядок вниз, в інструкції в другій клітинці написано: «Спростити». У третій клітинці y мінус 3 дорівнює 2 п'ятих х мінус 4.
    У четвертому рядку перша комірка говорить: «Запишіть рівняння в ухилово-перехопленому вигляді». Друга осередок порожня. У третій клітинці y дорівнює 2 п'ятих х мінус 1.

    Вправа\(\PageIndex{8}\)

    Знайдіть рівняння прямої з нахилом\(m=\frac{5}{6}\) і містить точку (6,3).

    Відповідь

    \(y=\frac{5}{6}x−2\)

    Вправа\(\PageIndex{9}\)

    Знайти рівняння прямої з нахилом\(m=\frac{2}{3}\) і містить точку (9,2).

    Відповідь

    \(y=\frac{2}{3}x−4\)

    ЗНАЙДІТЬ РІВНЯННЯ ПРЯМОЇ, ЗАДАНОЇ НАХИЛОМ І ТОЧКОЮ.
    1. Визначте ухил.
    2. Визначте точку.
    3. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
    4. Запишіть рівняння у формі нахилу—перехоплення.
    Вправа\(\PageIndex{10}\)

    Знайти рівняння прямої з нахилом\(m=−\frac{1}{3}\), що містить точку (6, −4). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Оскільки нам дано точку та нахил лінії, ми можемо підставити необхідні значення у форму точка-нахил\(y−y_{1}=m(x−x_{1})\).

    Визначте ухил. .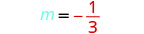
    Визначте точку. .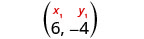
    Підставте значення на\(y−y_{1}=m(x−x_{1})\). .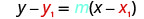
      .
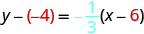
    Спростити. .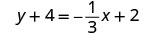
    Напишіть у формі нахилу—перехоплення. .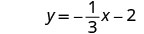
    Вправа\(\PageIndex{11}\)

    Знайти рівняння прямої з нахилом\(m=−\frac{2}{5}\) і містить точку (10, −5).

    Відповідь

    \(y=−\frac{2}{5}x−1\)

    Вправа\(\PageIndex{12}\)

    Знайти рівняння прямої з нахилом\(m=−\frac{3}{4}\) і містить точку (4, −7).

    Відповідь

    \(y=−\frac{3}{4}x−4\)

    Вправа\(\PageIndex{13}\)

    Знайти рівняння горизонтальної лінії, що містить точку (−1,2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Кожна горизонтальна лінія має нахил 0. Ми можемо замінити нахил і точки у форму точка-нахил,\(y−y_{1}=m(x−x_{1})\).

    Визначте ухил. .
    Визначте точку. .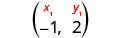
    Підставте значення на\(y−y_{1}=m(x−x_{1})\). .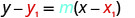
      .
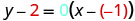
    Спростити. .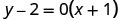
      .
      .
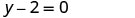
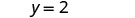
    Напишіть у формі нахилу—перехоплення. Він знаходиться у -формі, але може бути записаний y = 0x+2.
    Ми в кінцевому підсумку з формою горизонтальної лінії, y=a?
    Вправа\(\PageIndex{14}\)

    Знайти рівняння горизонтальної лінії, що містить точку (−3,8).

    Відповідь

    у = 8

    Вправа\(\PageIndex{15}\)

    Знайти рівняння горизонтальної лінії, що містить точку (−1,4).

    Відповідь

    у = 4

    Знайти рівняння прямої за двома точками

    Коли збираються реальні дані, лінійна модель може бути створена з двох точок даних. У наступному прикладі ми побачимо, як знайти рівняння прямої, коли задано лише дві точки.

    У нас є два варіанти пошуку рівняння прямої: нахил - перехоплення або точка-нахил. Оскільки ми будемо знати дві точки, буде більше сенсу використовувати форму точка-нахил.

    Але тоді нам потрібен ухил. Чи можемо ми знайти схил лише з двома точками? Так. Потім, коли ми маємо нахил, ми можемо використовувати його та одну з заданих точок, щоб знайти рівняння.

    Вправа\(\PageIndex{16}\): Find an Equation of a Line Given Two Points

    Знайдіть рівняння прямої, яка містить точки (5,4) і (3,6). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить математику. У першому рядку таблиці перша комірка зліва говорить: «Крок 1. Знайдіть нахил, використовуючи задані точки». Текст у другій клітинці говорить: «Щоб використовувати форму точка-нахил, спочатку знаходимо нахил». Третя комірка містить нахил формули рядка: m дорівнює y верхній індекс 2 мінус y верхній індекс 1 ділиться на x верхній індекс 2 мінус x верхній індекс 1. Нижче це m дорівнює 6 мінус 4 ділиться на 3 мінус 5. Нижче цього m дорівнює 2 ділиться на від'ємний 2. Нижче це m дорівнює негативному 1.У другому рядку перша клітинка говорить: «Крок 2. Виберіть одну точку». Друга клітинка говорить: «Виберіть будь-яку точку». Третя комірка містить впорядковану пару (5, 4) з верхнім індексом x нижнім рядком 1 над 5 та верхнім індексом y нижнім рядком 1 над 4.У третьому ряду перша клітинка говорить: «Крок 3. Підставляйте значення у форму точки-нахилу, y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках.» Верхній рядок другої клітинки залишаємо порожньою. Третя комірка містить форму нахилу точки, y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках. Нижче наведено точку нахилу форми з 5 заміненими на x індекс 1, 4 замінений на y індекс 1, а негативний 1 замінений на m: y мінус 4 дорівнює негативному 1 раз x мінус 5 у дужках. Нижче це у мінус 4 дорівнює негативний х плюс 5.У четвертому ряду перша клітина говорить: «Крок 4. Запишіть рівняння у формі ухил-перехоплення». Друга осередок порожня. Третя комірка містить y дорівнює негативному x плюс 9.

    Використовуйте точку (3,6) і подивіться, що ви отримаєте таке ж рівняння.

    Вправа\(\PageIndex{17}\)

    Знайти рівняння рядка, що містить точки (3,1) і (5,6).

    Відповідь

    \(y=\frac{5}{2}x−\frac{13}{2}\)

    Вправа\(\PageIndex{18}\)

    Знайдіть рівняння рядка, що містить точки (1,4) і (6,2).

    Відповідь

    \(y=−\frac{2}{5}x+\frac{22}{5}\)

    ЗНАЙДІТЬ РІВНЯННЯ ПРЯМОЇ, ЗАДАНОЇ ДВОМА ТОЧКАМИ.
    1. Знайдіть ухил, використовуючи задані точки.
    2. Виберіть один пункт.
    3. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
    4. Запишіть рівняння у формі нахилу—перехоплення.
    Вправа\(\PageIndex{19}\)

    Знайти рівняння рядка, що містить точки (−3, −1) та (2, −2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Оскільки ми маємо дві точки, ми знайдемо рівняння прямої, використовуючи форму точка-нахил. Першим кроком буде пошук ухилу.

    Знайти нахил прямої через (−3, −1) та (2, −2). .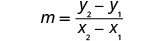
      .
      .
      .
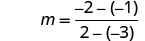
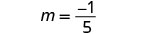
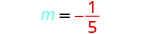
    Виберіть будь-яку точку. .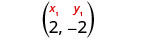
    Підставте значення на\(y−y_{1}=m(x−x_{1})\). .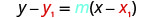
      .
      .
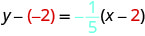
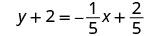
    Напишіть у формі нахилу—перехоплення. .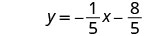
    Вправа\(\PageIndex{20}\)

    Знайти рівняння рядка, що містить точки (−2, −4) та (1, −3).

    Відповідь

    \(y=\frac{1}{3}x−\frac{10}{3}\)

    Вправа\(\PageIndex{21}\)

    Знайти рівняння рядка, що містить точки (−4, −3) та (1, −5).

    Відповідь

    \(y=−\frac{2}{5}x−\frac{23}{5}\)

    Вправа\(\PageIndex{22}\)

    Знайти рівняння рядка, що містить точки (−2,4) та (−2, −3). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Знову ж таки, першим кроком буде пошук ухилу.

    \(\begin{array}{lrl} \text { Find the slope of the line through }(-2,4) \text { and }(-2,-3) & & &\\ &m &=&\frac{y_{2}-x_{1}}{x_{2}-x_{1}} \\ &m &=&\frac{-3-4}{-2-(-2)} \\ &m &= &\frac{-7}{0} \\ \\ \text { The slope is undefined. } & & &\end{array}\)

    Це говорить нам, що це вертикальна лінія. Обидві наші точки мають координату x -2. Отже, наше рівняння прямої дорівнює x=−2. Оскільки yy немає, ми не можемо записати його у формі перехоплення нахилу.

    Можливо, ви захочете намалювати графік, використовуючи дві задані точки. Чи згоден графік з нашим висновком, що це вертикальна лінія?

    Вправа\(\PageIndex{23}\)

    Знайти рівняння рядка, що містить точки (5,1) та (5, −4).

    Відповідь

    х = 5

    Вправа\(\PageIndex{24}\)

    Знайти рівняння рядка, що містить точки (−4,4) та (−4,3).

    Відповідь

    x=−4

    Ми бачили, що ми можемо використовувати або форму нахилу - перехоплення, або форму точки - нахилу, щоб знайти рівняння прямої. Яку форму ми використовуємо, залежатиме від наданої нам інформації. Це підсумовано в табл\(\PageIndex{1}\).

    Написати рівняння прямої
    Якщо дано: Використання: Форма:
    Ухил і y -перехоплення ухил - перехоплення y = макс+б
    Нахил і точка точка-нахил \(y−y_{1}=m(x−x_{1})\)
    Дві точки точка-нахил \(y−y_{1}=m(x−x_{1})\)
    Таблиця\(\PageIndex{1}\)

    Знайти рівняння прямої, паралельної заданій прямій

    Припустимо, нам потрібно знайти рівняння прямої, яка проходить через певну точку і паралельна заданій прямій. Можна використовувати той факт, що паралельні лінії мають однаковий нахил. Таким чином, у нас буде точка і нахил - саме те, що нам потрібно використовувати рівняння точки - нахилу.

    Спочатку давайте подивимося на це графічно.

    На графіку показано графік y=2x−3. Ми хочемо побудувати графік прямої, паралельної цій лінії і проходить через точку (−2,1).

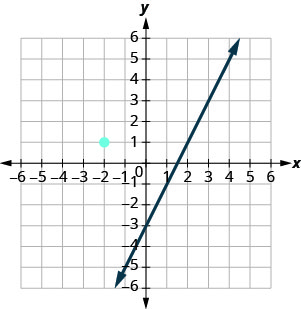
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої y дорівнює 2x мінус 3, перехоплює вісь y в (0, від'ємний 3) і перехоплює вісь x в (3 половини, 0). В іншому місці на графіку наноситься точка (від'ємна 2, 1).
    Малюнок\(\PageIndex{1}\)

    Ми знаємо, що паралельні лінії мають однаковий нахил. Отже, другий рядок матиме такий же нахил, як і y=2x−3. Цей нахил є\(m_{\|} = 2\). Ми будемо використовувати позначення\(m_{\|}\) для представлення нахилу прямої паралельної лінії з нахилом m. (Зверніть увагу, що індекс виглядає як дві паралельні лінії.)

    Другий рядок буде проходити через (−2,1) і мати m = 2. Для побудови графіка лінії ми починаємо з (−2,1) і відраховуємо підйом і біг. При m=2 (або\(m=\frac{2}{1}\)) відраховуємо підйом 2 і пробіг 1. Проводимо лінію.

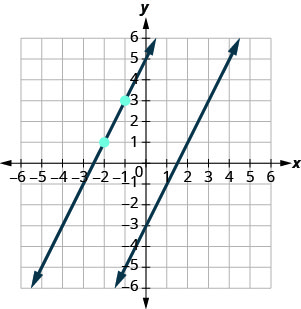
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої y дорівнює 2x мінус 3, перехоплює вісь y в (0, від'ємний 3) і перехоплює вісь x в (3 половини, 0). Виставляються точки (негативні 2, 1) і (негативні 1, 3). Друга лінія, паралельна першій, перехоплює вісь x at (негативні 5 половин, 0), проходить через точки (негативні 2, 1) і (негативні 1, 3) і перехоплює вісь y в (0, 5).
    Малюнок\(\PageIndex{2}\)

    Чи з'являються лінії паралельно? Чи проходить другий рядок (−2,1)?

    Тепер давайте подивимося, як це зробити алгебраїчно.

    Ми можемо використовувати форму нахилу - перехоплення або форму точки - нахилу, щоб знайти рівняння прямої. Тут ми знаємо одну точку і можемо знайти схил. Таким чином, ми будемо використовувати форму точка-нахил.

    Вправа\(\PageIndex{25}\): How to Find an Equation of a Line Parallel to a Given Line

    Знайти рівняння прямої, паралельної y=2x−3, що містить точку (−2,1). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

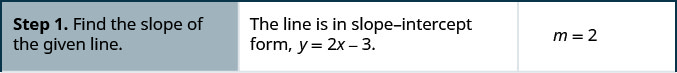
    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить математику. У першому рядку таблиці перша комірка зліва говорить: «Крок 1. Знайдіть нахил заданої лінії». Друга комірка говорить: «Лінія знаходиться у формі перехоплення нахилу. y дорівнює 2x мінус 3». Третя комірка містить нахил прямої, визначеної як m дорівнює 2.У другому рядку перша клітинка говорить: «Крок 2. Знайдіть нахил паралельної лінії». У другій клітинці написано «Паралельні лінії мають однаковий нахил». Третя комірка містить нахил паралельної лінії, визначеної як m паралель дорівнює 2.У третьому ряду в першій клітинці написано «Крок 3. Визначте точку». Друга клітинка читає «Задана точка є (негативна 2, 1)». Третя комірка містить впорядковану пару (від'ємний 2, 1) з верхнім індексом x нижнім рядком 1 над негативним 2 та верхнім індексом y нижнього індексу 1 над 1.У четвертому ряду в першій клітинці написано «Крок 4. Підставляйте значення у форму точки-нахилу, y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках.» Верх другої клітини порожній. Третя комірка містить форму нахилу точки, y мінус y індекс 1 дорівнює m разів x мінус x x індекс 1 у дужках. Нижче наведено форму з негативним 2, заміненим на x індекс 1, 1 замінений на y індекс 1, і 2 замінений на m: y мінус 1 дорівнює 2 рази x мінус 2 в дужках. Один рядок вниз, текст у другій клітинці говорить «Спростити». Правий стовпець містить y мінус 1 дорівнює 2 рази х плюс 2. Нижче це у мінус 1 дорівнює 2x плюс 4.У п'ятому ряду перша клітина говорить «Крок 5. Запишіть рівняння у формі ухил-перехоплення». Друга осередок порожня. Третя комірка містить y дорівнює 2x плюс 5.

    Чи має сенс це рівняння? Що таке y -перехоплення лінії? Що таке ухил?

    Вправа\(\PageIndex{26}\)

    Знайти рівняння прямої, паралельної лінії y=3x+1, яка містить точку (4,2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    y=3x−10

    Вправа\(\PageIndex{27}\)

    Знайдіть рівняння прямої, паралельної лінії\(y=\frac{1}{2}x−3\), яка містить точку (6,4).

    Відповідь

    \(y=\frac{1}{2}x+1\)

    ЗНАЙДІТЬ РІВНЯННЯ ПРЯМОЇ, ПАРАЛЕЛЬНОЇ ЗАДАНІЙ ЛІНІЇ.
    1. Знайдіть нахил заданої лінії.
    2. Знайдіть ухил паралельної лінії.
    3. Визначте точку.
    4. Підставляйте значення у форму «точка-нахил»,\(y−y_{1}=m(x−x_{1})\).
    5. Запишіть рівняння у формі нахилу—перехоплення.

    Знайти рівняння прямої, перпендикулярної заданій прямій

    Тепер розглянемо перпендикулярні лінії. Припустимо, нам потрібно знайти пряму, що проходить через певну точку і яка перпендикулярна заданій прямій. Можна використовувати той факт, що перпендикулярні лінії мають нахили, які є негативними зворотними. Ми знову будемо використовувати рівняння точка-нахил, як ми робили з паралельними лініями.

    На графіку показано графік y=2x−3. Тепер ми хочемо навести графік лінії, перпендикулярної до цієї лінії і проходячи через (−2,1).

    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої y дорівнює 2x мінус 3, перехоплює вісь y в (0, від'ємний 3) і перехоплює вісь x в (3 половини, 0). В іншому місці на графіку наноситься точка (від'ємна 2, 1).
    Малюнок\(\PageIndex{3}\)

    Ми знаємо, що перпендикулярні лінії мають нахили, які є негативними зворотними. Ми будемо використовувати позначення\(m_{\perp}\) для представлення нахилу прямої перпендикулярної лінії з нахилом m. (Зверніть увагу, що індекс\(_{\perp}\) виглядає як прямі кути, зроблені двома перпендикулярними лініями.)

    \[\begin{array}{cl}{y=2 x-3} & {\text { perpendicular line }} \\ {m=2} & {m_{\perp}=-\frac{1}{2}}\end{array}\]

    Тепер ми знаємо, що перпендикулярна лінія буде проходити через (−2,1) с\(m_{\perp}=−\frac{1}{2}\).

    Для побудови графіка лінії ми почнемо з (−2,1) і відрахуємо підйом −1 та пробіг 2. Потім проводимо лінію.

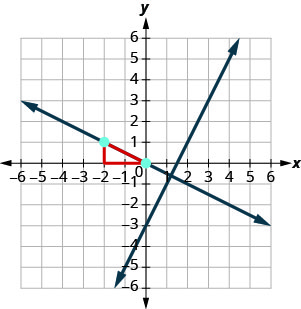
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої y дорівнює 2x мінус 3, перехоплює вісь y в (0, від'ємний 3) і перехоплює вісь x в (3 половини, 0). В іншому місці наноситься точка (мінус 2, 1). Інша лінія, перпендикулярна першій лінії, проходить через точку (від'ємна 2, 1) і перехоплює осі x і y в (0, 0). Червона лінія зі стрілкою тягнеться вліво від (0, 0) до (негативний 2, 0), потім тягнеться вгору і закінчується на (негативний 2, 1), утворюючи прямокутний трикутник з другою лінією як гіпотенуза.
    Малюнок\(\PageIndex{4}\)

    Чи з'являються лінії перпендикулярно? Чи проходить другий рядок (−2,1)?

    Тепер давайте подивимося, як це зробити алгебраїчно. Ми можемо використовувати форму нахилу - перехоплення або форму точки - нахилу, щоб знайти рівняння прямої. У цьому прикладі ми знаємо одну точку і можемо знайти нахил, тому ми будемо використовувати форму точка-нахил.

    Вправа\(\PageIndex{28}\)

    Знайти рівняння прямої, перпендикулярної y=2x−3, що містить точку (−2,1). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить математику. У першому рядку таблиці перша комірка зліва говорить: «Крок 1. Знайдіть нахил заданої лінії». Друга комірка говорить: «Лінія знаходиться у формі перехоплення нахилу. y дорівнює 2x мінус 3». Третя комірка містить нахил прямої, визначеної як m дорівнює 2.
    У другому рядку в першій клітинці написано «Крок 2. Знайдіть нахил перпендикулярної лінії». У другій клітинці написано «Нахили перпендикулярних ліній негативні зворотні». Третя комірка містить m дорівнює від'ємній половині.
    У третьому ряду в першій клітинці написано «Крок 3. Визначте точку». Друга клітинка читає «Задана точка є (негативна 2, 1)». Третя комірка містить впорядковану пару (від'ємний 2, 1) з верхнім індексом x нижнім рядком 1 над негативним 2 та верхнім індексом y нижнього індексу 1 над 1.
    У четвертому ряду перша клітина говорить «Крок 4. Підставте значення у форму точки-нахилу». У другій клітці написано: «Спростити». Третя клітина показує цю роботу, що закінчується y - 1 = - 1/2 х - 1.
    У п'ятому ряду перша клітина говорить «Крок 5. Запишіть рівняння у формі ухил-перехоплення». Друга осередок порожня. Третя комірка містить y дорівнює від'ємній 1 половині x.

    Вправа\(\PageIndex{29}\)

    Знайти рівняння прямої, перпендикулярної лінії y=3x+1, яка містить точку (4,2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    \(y=−\frac{1}{3}x+\frac{10}{3}\)

    Вправа\(\PageIndex{30}\)

    Знайдіть рівняння прямої, перпендикулярної лінії\(y=\frac{1}{2}x−3\), яка містить точку (6,4).

    Відповідь

    y=−2x+16

    ЗНАЙДІТЬ РІВНЯННЯ ПРЯМОЇ, ПЕРПЕНДИКУЛЯРНОЇ ЗАДАНІЙ ЛІНІЇ.
    1. Знайдіть нахил заданої лінії.
    2. Знайдіть нахил перпендикулярної лінії.
    3. Визначте точку.
    4. Підставляйте значення у форму «точка-нахил»,\(y−y_{1}=m(x−x_{1})\).
    5. Запишіть рівняння у формі нахилу—перехоплення.
    Вправа\(\PageIndex{31}\)

    Знайти рівняння прямої, перпендикулярної x=5, що містить точку (3, −2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Знову ж таки, оскільки ми знаємо одну точку, варіант точка-нахил здається більш перспективним, ніж варіант перехоплення нахилу. Нам потрібен нахил, щоб використовувати цю форму, і ми знаємо, що нова лінія буде перпендикулярна x = 5. Ця лінія вертикальна, тому її перпендикуляр буде горизонтальним. Це говорить нам про\(m_{\perp}=0\).

    \(\begin{array}{lrll}{\text { Identify the point. }} &{(3}&{,}&{-2)}\\ {\text { Identify the slope of the perpendicular line. }} & {m_{\perp}}&{=}&{0} \\ {\text { Substitute the values into } y-y_{1}=m\left(x-x_{1}\right) .} & {y-y_{1}}&{=}&{m\left(x-x_{1}\right)} \\{} &{y−(−2)}&{=}&{0(x−3)} \\{\text { Simplify. }} & {y+2}&{=}&{0} \\ &{y}&{=}&{-2}\end{array}\)

    Намалюйте графік обох ліній. Чи здаються вони перпендикулярними?

    Вправа\(\PageIndex{32}\)

    Знайти рівняння прямої, яка перпендикулярна до прямої x = 4, що містить точку (4, −5). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    y=−5

    Вправа\(\PageIndex{33}\)

    Знайти рівняння прямої, яка перпендикулярна до прямої x=2, яка містить точку (2, −1). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    y=−1

    У\(\PageIndex{31}\) Вправі ми використовували форму точка-нахил, щоб знайти рівняння. Ми могли б подивитися на це по-іншому.

    Ми хочемо знайти пряму перпендикулярну x=5, яка містить точку (3, −2). Графік показує нам лінію x = 5 і точку (3, −2).

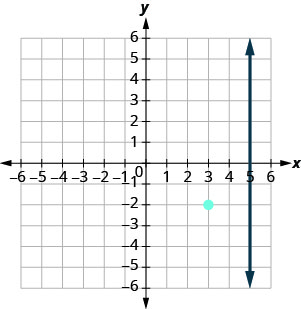
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої дорівнює x, дорівнює 5, перехоплює вісь x в (5, 0) і проходить паралельно осі y. В іншому місці на графіку наноситься точка (3, від'ємна 2).
    Малюнок\(\PageIndex{5}\)

    Ми знаємо, що кожна лінія, перпендикулярна вертикальній лінії, є горизонтальною, тому ми намалюємо горизонтальну лінію через (3, −2).

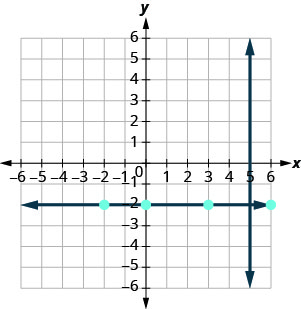
    На графіку показана координатна площина x y. Осі x та y проходять від негативних 7 до 7. Лінія, рівняння якої дорівнює x, дорівнює 5, перехоплює вісь x в (5, 0) і проходить паралельно осі y. В іншому місці на графіку нанесені точки (від'ємний 2, від'ємний 2), (0, від'ємний 2), (3, негативний 2) та (6, негативний 2). Лінія, перпендикулярна попередній лінії, проходить через ці точки і проходить паралельно осі х.
    Малюнок\(\PageIndex{6}\)

    Чи з'являються лінії перпендикулярно?

    Якщо ми подивимось на кілька точок на цій горизонтальній лінії, ми помітимо, що всі вони мають y -координати −2. Отже, рівняння прямої, перпендикулярної вертикальній лінії x=5, дорівнює y=−2.

    Вправа\(\PageIndex{34}\)

    Знайти рівняння прямої, перпендикулярної y=−4, що містить точку (−4,2). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    Рядок y=−4 є горизонтальною лінією. Будь-яка перпендикулярна їй пряма повинна бути вертикальною, у вигляді x=a. Оскільки перпендикулярна пряма вертикальна і проходить через неї (−4,2), кожна точка на ній має координату x -4. Рівняння перпендикулярної прямої дорівнює x=−4. Можливо, ви захочете намалювати лінії. Чи з'являються вони перпендикулярно?

    Вправа\(\PageIndex{35}\)

    Знайти рівняння прямої, яка перпендикулярна до прямої y=1, яка містить точку (−5,1). Запишіть рівняння у формі нахилу—перехоплення.

    Відповідь

    x=−5

    Вправа\(\PageIndex{36}\)

    Знайти рівняння прямої, перпендикулярної прямому y=−5, що містить точку (−4, −5).

    Відповідь

    x=−4

    Примітка

    Отримайте доступ до цього інтернет-ресурсу для отримання додаткової інструкції та практики з пошуком рівняння лінії.

    Ключові поняття

    • Знайти рівняння прямої з заданим нахилом і точкою
      1. Визначте ухил.
      2. Визначте точку.
      3. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
      4. Запишіть рівняння у вигляді ухил-перехоплення.
    • Знайти рівняння прямої заданих двох точок
      1. Знайдіть ухил, використовуючи задані точки.
      2. Виберіть один пункт.
      3. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
      4. Запишіть рівняння у вигляді ухил-перехоплення.
    • Записати і рівняння прямої
      • Якщо задано нахил і\(y\) -перехоплення, використовуйте форму нахилу — перехоплення\(y=mx+b\).
      • Якщо вказано нахил і точку, використовуйте форму «точка — нахил»\(y−y_{1}=m(x−x_{1})\).
      • Якщо задано дві точки, використовуйте форму «точка — нахил»\(y−y_{1}=m(x−x_{1})\).
    • Знайти рівняння прямої, паралельної заданій прямій
      1. Знайдіть нахил заданої лінії.
      2. Знайдіть ухил паралельної лінії.
      3. Визначте точку.
      4. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
      5. Запишіть рівняння у вигляді ухил-перехоплення.
    • Знайти рівняння прямої, перпендикулярної заданій прямій
      1. Знайдіть нахил заданої лінії.
      2. Знайдіть нахил перпендикулярної лінії.
      3. Визначте точку.
      4. Підставляємо значення в точку-нахил форми,\(y−y_{1}=m(x−x_{1})\).
      5. Запишіть рівняння у вигляді ухил-перехоплення.

    Глосарій

    точка — форма нахилу
    Точка-нахил форми рівняння прямої з нахилом мм і містить точку\(\left(x_{1}, y_{1}\right)\)\(y-y_{1}=m\left(x-x_{1}\right)\).