1.10E: Вправи
- Page ID
- 59080
Практика робить досконалим
Використання комутативних та асоціативних властивостей
У наступних вправах використовуйте асоціативне властивість для спрощення.
\(3(4x)\)
- Відповідь
-
\(12x\)
\(4(7m)\)
\((y+12)+28\)
- Відповідь
-
\(y+40\)
\((n+17)+33\)
У наступних вправах спростити.
\(\frac{1}{2}+\frac{7}{8}+\left(-\frac{1}{2}\right)\)
- Відповідь
-
\(\frac{7}{8}\)
\(\frac{2}{5}+\frac{5}{12}+\left(-\frac{2}{5}\right)\)
\(\frac{3}{20} \cdot \frac{49}{11} \cdot \frac{20}{3}\)
- Відповідь
-
\(\frac{49}{11}\)
\(\frac{13}{18} \cdot \frac{25}{7} \cdot \frac{18}{13}\)
\(-24 \cdot 7 \cdot \frac{3}{8}\)
- Відповідь
-
\(-63\)
\(-36 \cdot 11 \cdot \frac{4}{9}\)
\(\left(\frac{5}{6}+\frac{8}{15}\right)+\frac{7}{15}\)
- Відповідь
-
\(1 \frac{5}{6}\)
\(\left(\frac{11}{12}+\frac{4}{9}\right)+\frac{5}{9}\)
\(17(0.25)(4)\)
- Відповідь
-
\(17\)
\(36(0.2)(5)\)
\([2.48(12)](0.5)\)
- Відповідь
-
\(14.88\)
\([9.731(4)](0.75)\)
\(7(4a)\)
- Відповідь
-
\(28a\)
\(9(8w)\)
\(-15(5m)\)
- Відповідь
-
\(-75m\)
\(-23(2n)\)
\(12(\frac{5}{6}p)\)
- Відповідь
-
\(10p\)
\(20(\frac{3}{5}q)\)
\(43 m+(-12 n)+(-16 m)+(-9 n)\)
- Відповідь
-
\(27m+(-21n)\)
\(-22p+17q+(-35p)+(-27q)\)
\(\frac{3}{8} g+\frac{1}{12} h+\frac{7}{8} g+\frac{5}{12} h\)
- Відповідь
-
\(\frac{5}{4}g+\frac{1}{2}h\)
\(\frac{5}{6} a+\frac{3}{10} b+\frac{1}{6} a+\frac{9}{10} b\)
\(6.8 p+9.14 q+(-4.37 p)+(-0.88 q)\)
- Відповідь
-
\(2.43p+8.26q\)
\(9.6 m+7.22 n+(-2.19 m)+(-0.65 n)\)
Використання ідентичності та обернених властивостей додавання та множення
У наступних вправах знайдіть добавку, обернену кожним числом
- \(\frac{2}{5}\)
- \(4.3\)
- \(-8\)
- \(-\frac{10}{3}\)
- Відповідь
-
- \(-\frac{2}{5}\)
- \(-4.3\)
- \(8\)
- \(\frac{10}{3}\)
- \(\frac{5}{9}\)
- \(2.1\)
- \(-3\)
- \(-\frac{9}{5}\)
- \(-\frac{7}{6}\)
- \(-0.075\)
- \(23\)
- \(\frac{1}{4}\)
- Відповідь
-
- \(\frac{7}{6}\)
- \(0.075\)
- \(-23\)
- \(-\frac{1}{4}\)
- \(-\frac{8}{3}\)
- \(-0.019\)
- \(52\)
- \(\frac{5}{6}\)
У наступних вправах знайдіть мультиплікативний зворотний кожного числа.
- \(6\)
- \(-\frac{3}{4}\)
- \(0.7\)
- Відповідь
-
- \(\frac{1}{6}\)
- \(-\frac{4}{3}\)
- \(\frac{10}{7}\)
- \(12\)
- \(-\frac{9}{2}\)
- \(0.13\)
- \(\frac{11}{12}\)
- \(-1.1\)
- \(-4\)
- Відповідь
-
- \(\frac{12}{11}\)
- \(-\frac{10}{11}\)
- \(-\frac{1}{4}\)
- \(\frac{17}{20}\)
- \(-1.5\)
- \(-3\)
Використовувати властивості нуля
У наступних вправах спростити.
\(\frac{0}{6}\)
- Відповідь
-
\(0\)
\(\frac{3}{0}\)
\(0 \div \frac{11}{12}\)
- Відповідь
-
\(0\)
\(\frac{6}{0}\)
\(\frac{0}{3}\)
- Відповідь
-
\(0\)
\(0 \cdot \frac{8}{15}\)
\((-3.14)(0)\)
- Відповідь
-
\(0\)
\(\frac{\frac{1}{10}}{0}\)
Змішана практика
У наступних вправах спростити.
\(19 a+44-19 a\)
- Відповідь
-
\(44\)
\(27 c+16-27 c\)
\(10(0.1 d)\)
- Відповідь
-
\(1d\)
\(100(0.01 p)\)
\(\frac{0}{u-4.99}, \text { where } u \neq 4.99\)
- Відповідь
-
\(0\)
\(\frac{0}{v-65.1}, \text { where } v \neq 65.1\)
\(0 \div\left(x-\frac{1}{2}\right), \text { where } x \neq \frac{1}{2}\)
- Відповідь
-
\(0\)
\(0 \div\left(y-\frac{1}{6}\right), \text { where } y \neq \frac{1}{6}\)
\(\frac{32-5 a}{0}, \text { where } 32-5a \neq 0\)
- Відповідь
-
невизначений
\(\frac{28-9 b}{0}, \text { where } 28-9b \neq 0\)
\(\left(\frac{3}{4}+\frac{9}{10} m\right) \div 0 \text { where } \frac{3}{4}+\frac{9}{10}m \neq 0\)
- Відповідь
-
невизначений
\(\left(\frac{5}{16} n-\frac{3}{7}\right) \div 0 \text { where } \frac{5}{16} n-\frac{3}{7} \neq 0\)
\(15 \cdot \frac{3}{5}(4 d+10)\)
- Відповідь
-
\(36d+90\)
\(18 \cdot \frac{5}{6}(15 h+24)\)
Спрощення виразів за допомогою властивості розподілу
У наступних вправах спростіть використання розподільного властивості.
\(8(4 y+9)\)
- Відповідь
-
\(32y+72\)
\(9(3 w+7)\)
\(6(c-13)\)
- Відповідь
-
\(6c-78\)
\(7(y-13)\)
\(\frac{1}{4}(3 q+12)\)
- Відповідь
-
\(\frac{3}{4}q+3\)
\(\frac{1}{5}(4 m+20)\)
\(9\left(\frac{5}{9} y-\frac{1}{3}\right)\)
- Відповідь
-
\(5y-3\)
\(10\left(\frac{3}{10} x-\frac{2}{5}\right)\)
\(12\left(\frac{1}{4}+\frac{2}{3} r\right)\)
- Відповідь
-
\(3+8r\)
\(12\left(\frac{1}{6}+\frac{3}{4} s\right)\)
\(r(s-18)\)
- Відповідь
-
\(rs-18r\)
\(u(v-10)\)
\((y+4) p\)
- Відповідь
-
\(yp+4p\)
\((a+7) x\)
\(-7(4 p+1)\)
- Відповідь
-
\(-28p-7\)
\(-9(9 a+4)\)
\(-3(x-6)\)
- Відповідь
-
\(-3x+18\)
\(-4(q-7)\)
\(-(3 x-7)\)
- Відповідь
-
\(-3x+7\)
\(-(5 p-4)\)
\(16-3(y+8)\)
- Відповідь
-
\(-3y-8\)
\(18-4(x+2)\)
\(4-11(3 c-2)\)
- Відповідь
-
\(-33c+26\)
\(9-6(7 n-5)\)
\(22-(a+3)\)
- Відповідь
-
\(-a+19\)
\(8-(r-7)\)
\((5 m-3)-(m+7)\)
- Відповідь
-
\(4m-10\)
\((4 y-1)-(y-2)\)
\(5(2 n+9)+12(n-3)\)
- Відповідь
-
\(22n+9\)
\(9(5 u+8)+2(u-6)\)
\(9(8 x-3)-(-2)\)
- Відповідь
-
\(72x-25\)
\(4(6 x-1)-(-8)\)
\(14(c-1)-8(c-6)\)
- Відповідь
-
\(6c+34\)
\(11(n-7)-5(n-1)\)
\(6(7 y+8)-(30 y-15)\)
- Відповідь
-
\(12y+63\)
\(7(3 n+9)-(4 n-13)\)
Щоденна математика
Страхова доплата Керрі повинна була зробити 5 заправок. Кожна начинка коштувала 80 доларів. Її стоматологічне страхування вимагало від неї сплатити 20% від вартості як копію. Обчисліть копію Керрі:
- По-перше, помноживши 0,20 на 80, щоб знайти її копію для кожного заповнення, а потім помноживши свою відповідь на 5, щоб знайти її загальну копію для 5 начинок.
- Далі, множивши [5 (0.20)] (80)
- Яка з властивостей дійсних чисел говорить про те, що ваші відповіді на частини (а), де ви помножили 5 [(0,20) (80)] і (b), де ви помножили [5 (0,20)] (80), повинні бути рівні?
- Відповідь
-
- $80
- $80
- відповіді будуть відрізнятися
Час приготування Хелен купила 24-фунтову індичку для вечері на День подяки своєї родини і хоче знати, в який час поставити індичку в духовку. Вона хоче, щоб 20 хвилин на фунт час приготування. Розрахуйте тривалість часу, необхідного для смаження індички:
- По-перше, множивши 24 · 20, щоб знайти загальну кількість хвилин, а потім помноживши відповідь\(\frac{1}{60}\) на перетворення хвилин у години.
- Далі, шляхом множення\(24(20 \cdot \frac{1}{60})\).
- Яка з властивостей дійсних чисел говорить про те, що ваші відповіді на частини (а), де ви помножили\((24 \cdot 20) \frac{1}{60}\), і (б), де ви множили\(24(20 \cdot \frac{1}{60})\), повинні бути рівні?
Купуючи за кейсом Трейдер Джо продуктові магазини продали пляшку вина, яку вони назвали «Two Buck Chuck» за $1.99. Вони продали футляр з 12 пляшок за $23,88. Щоб знайти вартість 12 пляшок у розмірі 1,99 дол. США, зверніть увагу, що 1.99 дорівнює 2−0,01.
- Помножте 12 (1,99), використовуючи розподільну властивість, щоб помножити 12 (2−0,01).
- Чи було вигідною купівлею «Два Бак-Чака» по справі?
- Відповідь
-
- $23.88
- немає, ціна однакова
Multi-pack купити шампунь Adele's продається за $3,99 за пляшку в продуктовому магазині. У складському магазині такий же шампунь продається як 3 упаковки за $10,49. Щоб знайти вартість пляшок 3 в $3.99, зверніть увагу, що 3.99 дорівнює 4−0,01.
- Помножте 3 (3,99), використовуючи розподільну властивість, щоб помножити 3 (4−0,01).
- Скільки б Адель заощадила, купивши 3 пляшки в складському магазині, а не в продуктовому магазині?
Письмові вправи
Своїми словами, викласти комутативну властивість додавання.
- Відповідь
-
\(Answers may vary\)
У чому різниця між адитивним оберненим і мультиплікативним оберненим числом?
Спростіть\(8(x-\frac{1}{4})\) використання властивості distributive і пояснити кожен крок.
- Відповідь
-
\(Answers may vary\)
Поясніть, як ви можете помножити 4 ($5,97) без паперу чи калькулятора, подумавши про $5.97 як 6−0,03, а потім використавши розподільну властивість.
Самостійна перевірка
ⓐ Після виконання вправ скористайтеся цим контрольним списком, щоб оцінити своє володіння цілями цього розділу.
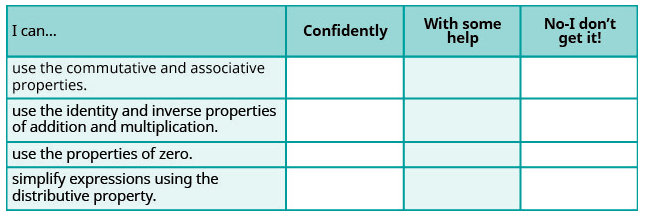
ⓑ Ознайомившись з цим контрольним списком, що ви робите, щоб стати впевненими у всіх цілях?
