Skip to main content
LibreTexts - Ukrayinska

1.2: Вступ до цілих чисел

  1. Last updated
  2. Save as PDF
  • Page ID
    59027

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання
    • До кінця цього розділу ви зможете:
    • Використовуйте значення місця з цілими числами
    • Визначте кратні та застосуйте тести на подільність
    • Знайти прості множники та найменш поширені множники

    Коли ми починаємо вивчення елементарної алгебри, нам потрібно освіжити деякі наші навички та словниковий запас. У цій главі мова піде про цілі числа, цілі числа, дроби, десяткові та дійсні числа. Ми також почнемо використовувати алгебраїчні позначення та словниковий запас.

    Використовувати значення місця з цілими числами

    Найосновнішими числами, які використовуються в алгебрі, є числа\(1, 2, 3, 4\), які ми використовуємо для підрахунку об'єктів у нашому світі: і так далі. Вони називаються рахунковими числами s. Підрахунок чисел ще називають натуральними числами. Якщо до рахункових чисел додати нуль, то отримаємо набір цілих чисел s.

    • Підрахунок чисел:\(1, 2, 3, …\)
    • Цілі числа:\(0, 1, 2, 3, …\)

    Позначення «\(…\)» називається крапкою і означає «і так далі», або що візерунок триває нескінченно.

    Ми можемо візуалізувати підрахунок чисел і цілих чисел на числовому рядку (див. Рисунок\(\PageIndex{1}\)).

    Внизу діаграми проходить горизонтальна цифрова лінія зі стрілками на кожному кінці і значеннями від нуля до шести. Друга горизонтальна лінія зі стрілкою вліво лежить над першою і простягається від нуля до трьох. Ця лінія має маркування «менший». Третя горизонтальна лінія зі стрілкою, спрямованою вправо, лежить над першими двома, але проходить від трьох до шести і позначається «більше».
    Малюнок\(\PageIndex{1}\): Числа на числовому рядку стають більшими, коли вони йдуть зліва направо, і меншими, коли вони йдуть справа наліво. Хоча цей номер рядка показує тільки цілі числа\(0\) через\(6\), цифри продовжують йти без кінця.

    Виконання діяльності з маніпулятивної математики «Числова лінія-Частина 1» допоможе вам розвинути краще розуміння підрахунку чисел і цілих чисел.

    Наша система числення називається системою значень місця, тому що значення цифри залежить від її положення в числі. На малюнку\(\PageIndex{2}\) показані значення місця. Значення місця поділяються на групи по три, які називаються періодами. Періоди - одиниці, тисячі, мільйони, мільярди, трильйони тощо. У письмовому числі коми відокремлюють крапки.

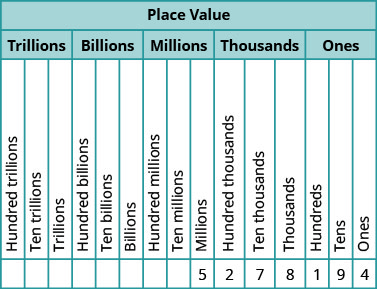
    Ця цифра являє собою таблицю, що ілюструє число 5 278 194 в системі значень місця. Таблиця відображається рядком заголовка з написом «Place Value», розділеним на другий рядок заголовка з написом «Трильйони», «Мільйони», «Мільйони», «Тисячі» та «Одиниці». Під заголовком «Трильйони» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто трильйонів», «Десять трильйонів» і «Трильйони». Під заголовком «Мільярди» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто мільярдів», «Десять мільярдів» і «Мільярди». Під заголовком «Мільйони» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто мільйонів», «Десять мільйонів» і «Мільйони». Під заголовком «Тисячі» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто тисяч», «Десять тисяч» і «Тисячі». Під заголовком «Одиниці» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сотні», «Десятки» і «Одиниці». Зліва направо, під стовпцями з написом «Мільйони», «Сто тисяч», «Десять тисяч», «Тисячі», «Сотні», «Десятки» та «Одиниці», наведені наступні значення: 5, 2, 7, 8, 1, 9, 4. Це означає, що існує 5 мільйонів, 2 сотні тисяч, 7 десять тисяч, 8 тисяч, 1 сотні, 9 десятків і 4 в кількості п'ять мільйонів двісті сімдесят дев'ять тисяч сто дев'яносто чотири.
    Малюнок\(\PageIndex{2}\): Число\(5278194\) показано на графіку. Цифра\(5\) знаходиться в мільйонному місці. Цифра\(2\) знаходиться в стотисячному місці. Цифра\(7\) знаходиться в десятитисячному місці. Цифра\(8\) знаходиться в тисячах місце. Цифра\(1\) знаходиться в сотні місце. Цифра\(9\) знаходиться в десятках місці. Цифра\(4\) знаходиться в одному місці.
    Вправа\(\PageIndex{1}\)

    У числі\(63407218\) знайдіть місце значення кожної цифри:

    1. \(7\)
    2. \(0\)
    3. \(1\)
    4. \(6\)
    5. \(3\)
    Відповідь

    Помістіть число в діаграмі значень місця:

    Ця цифра являє собою таблицю, що ілюструє число 63 407 218 в системі значень місця. Таблиця відображається рядком заголовка з написом «Place Value», розділеним на другий рядок заголовка з написом «Трильйони», «Мільйони», «Мільйони», «Тисячі» та «Одиниці». Під заголовком «Трильйони» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто трильйонів», «Десять трильйонів» і «Трильйони». Під заголовком «Мільярди» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто мільярдів», «Десять мільярдів» і «Мільярди». Під заголовком «Мільйони» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто мільйонів», «Десять мільйонів» і «Мільйони». Під заголовком «Тисячі» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сто тисяч», «Десять тисяч» і «Тисячі». Під заголовком «Одиниці» знаходяться три позначені стовпці, написані знизу вгору, які читають «Сотні», «Десятки» і «Одиниці». Зліва направо, нижче стовпців з написом «Десять мільйонів», «Мільйони», «Сто тисяч», «Десять тисяч», «Тисячі», «Сотні», «Десятки» та «Одиниці», наведені наступні значення: 6, 3, 4, 0, 7, 2, 1, 8. Це означає, що існує 6 десять мільйонів, 3 мільйони, 4 сотні тисяч, 0 десять тисяч, 7 тисяч, 2 сотні, 1 десять і 8 в кількості шістдесят три мільйони, чотириста сім тисяч, двісті вісімнадцять.
    1. Він\(7\) знаходиться в тисячах місць.
    2. Він\(0\) знаходиться в десятьтисячному місці.
    3. The\(1\) знаходиться в десятках місце.
    4. Він\(6\) знаходиться в десятимільйонному місці.
    5. Він\(3\) знаходиться в мільйонному місці.
    Вправа\(\PageIndex{2}\)

    Для числа\(27493615\) знайдіть місце значення кожної цифри:

    1. 2
    2. 1
    3. 4
    4. 7
    5. 5
    Відповідь
    1. десять мільйонів
    2. десятки
    3. сто тисяч
    4. мільйони
    5. одиничні
    Вправа\(\PageIndex{3}\)

    Для числа\(519711641328\) знайдіть місце значення кожної цифри:

    1. 9
    2. 4
    3. 2
    4. 6
    5. 7
    Відповідь
    1. мільярди
    2. десять тисяч
    3. десятки
    4. сто тисяч
    5. сто мільйонів

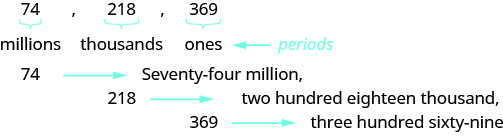
    Коли ви пишете чек, ви виписуєте номер як словами, так і цифрами. Щоб написати число словами, напишіть число в кожному крапці, а потім назву періоду, без s в кінці. Почніть зліва, де періоди мають найбільше значення. Тих період не названий. Коми розділяють крапки, тому всюди, де в числі є кома, ставте кому між словами (див. Рис.\(\PageIndex{3}\)). Число\(74218369\) пишеться як сімдесят чотири мільйони, двісті вісімнадцять тисяч, триста шістдесят дев'ять.

    На цьому малюнку цифри 74, 218 і 369 перераховані поспіль, розділені комами. Кожне число має фігурну дужку під ним із словом «мільйони», написаним під номером 74, «тисячі», написаним під цифрою 218, а «одиниці» написані під номером 369. Стрілка, спрямована вліво, вказує на ці три слова, позначаючи їх «періодами». Один рядок вниз - цифра «74», стрілка вправо і слова «сімдесят чотири мільйони», за якими слід кома. Наступний рядок нижче - цифра «218», стрілка вправо і слова «двісті вісімнадцять тисяч», за якими слід кома. На нижньому ряду знаходиться цифра «369», спрямована вправо стрілка і слова «триста шістдесят дев'ять».
    Малюнок\(\PageIndex{3}\)
    НАЗВІТЬ ЦІЛЕ ЧИСЛО СЛОВАМИ.
    1. Почніть ліворуч і назвіть номер у кожному періоді, а потім назву періоду.
    2. Поставте коми в число, щоб відокремити періоди.
    3. Не називайте ті період.
    Вправа\(\PageIndex{4}\)

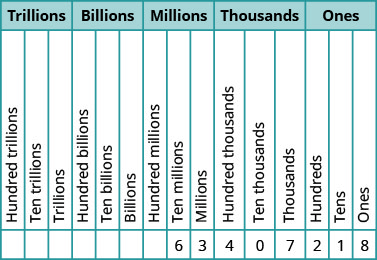
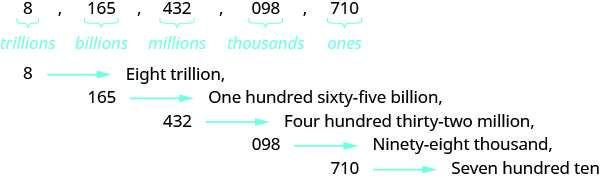
    Назвіть число\(8165432098710\) за допомогою слів.

    Відповідь

    Назвіть номер у кожному періоді, а потім назву періоду.

    На цьому малюнку цифри 8, 165, 432, 098 і 710 перераховані в рядку, розділені комами. Кожне число має горизонтальну дужку під словом «трильйони», написане під числом 8, «мільярди» написано під числом 165, «мільйони» написані під числом 432, «тисячі» написані під номером 098, і «ті», написані під номером 710. Один рядок вниз - це число 8, стрілка вправо і слова «Вісім трильйонів», за якими слідує кома. На наступному рядку нижче цифра 165, стрілка вправо і слова «Сто шістдесят п'ять мільярдів», за якими слід кома. На наступному рядку нижче цифра 432, стрілка вправо і слова «Чотириста тридцять два мільйони», за якими слід кома. На наступному рядку нижче цифра «098», стрілка вправо і слова «дев'яносто вісім тисяч», за якими слід кома. На нижньому ряду знаходиться число 710, спрямована вправо стрілка і слова «сімсот десять».

    Покладіть коми, щоб розділити періоди.

    Так,\(8165432098710\) названий як вісім трильйонів, сто шістдесят п'ять мільярдів, чотириста тридцять два мільйони, дев'яносто вісім тисяч, сімсот десять.

    Вправа\(\PageIndex{5}\)

    Назвіть число 9,258,137,904,0619,258,137,904,061, використовуючи слова.

    Відповідь

    дев'ять трильйонів двісті п'ятдесят вісім мільярдів, сто тридцять сім мільйонів, дев'ятсот чотири тисячі, шістдесят один

    Вправа\(\PageIndex{6}\)

    Назвіть число 17 864,325,619,00417,864,325,619,004, використовуючи слова.

    Відповідь

    сімнадцять трильйонів, вісімсот шістдесят чотири мільярди, триста двадцять п'ять мільйонів, шістсот дев'ятнадцять тисяч чотири

    Тепер ми збираємося змінити процес, записуючи цифри з назви номера. Щоб записати число цифрами, спочатку шукаємо підказкові слова, які вказують на періоди. Корисно намалювати три пробіли для потрібних періодів, а потім заповнити пробіли цифрами, розділяючи крапки комами.

    ЗАПИШІТЬ ЦІЛЕ ЧИСЛО, ВИКОРИСТОВУЮЧИ ЦИФРИ.
    1. Визначте слова, які вказують на періоди. (Пам'ятайте, що ті період ніколи не називаються.)
    2. Намалюйте три заготовки, щоб вказати кількість місць, необхідних в кожному періоді. Розділіть періоди комами.
    3. Назвіть номер у кожному періоді та розмістіть цифри у правильній позиції значення місця.
    Вправа\(\PageIndex{7}\)

    Запишіть дев'ять мільярдів, двісті сорок шість мільйонів, сімдесят три тисячі, сто вісімдесят дев'ять як ціле число, використовуючи цифри.

    Відповідь

    Визначте слова, які вказують на періоди.
    За винятком першого періоду, всі інші періоди повинні мати три місця. Намалюйте три заготовки, щоб вказати кількість місць, необхідних в кожному періоді. Розділіть періоди комами.
    Потім запишіть цифри в кожному періоді.

    Зображення має два рядки тексту. У верхніх рядках написано «дев'ять мільярдів», за ними йде кома, і «двісті сорок шість мільйонів», за якими також слід кома. Слова «мільярд» і «мільйон» підкреслені, і кожна фраза має фігурну дужку під ним. У нижніх рядках написано «сімдесят три тисячі», за ними йде кома, і «сто вісімдесят дев'ять». Слово «тисяча» підкреслено, і кожна фраза має фігурну дужку під ним.

    Число — 9 246 073 189.
    Вправа\(\PageIndex{8}\)

    Напишіть число два мільярди, чотириста шістдесят шість мільйонів, сімсот чотирнадцять тисяч, п'ятдесят один як ціле число, використовуючи цифри.

    Відповідь

    2 466 714,051

    Вправа\(\PageIndex{9}\)

    Напишіть число одинадцять мільярдів, дев'ятсот двадцять один мільйон, вісімсот тридцять тисяч, сто шість як ціле число за допомогою цифр.

    Відповідь

    11 921 830,106

    У 2013 році Бюро перепису населення США оцінило чисельність населення штату Нью-Йорк в 19 651 127 осіб. Можна сказати, що населення Нью-Йорка становило приблизно 20 мільйонів. У багатьох випадках вам не потрібно точне значення; приблизне число досить добре.

    Процес наближення числа називається округленням. Числа округляються до певного значення місця, в залежності від того, наскільки потрібна точність. Сказати, що населення Нью-Йорка становить приблизно 20 мільйонів, означає, що ми округлили до мільйонів місць.

    Вправа\(\PageIndex{10}\) How to Round Whole Numbers

    Навколо 23 658 до найближчої сотні.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Друга графа містить подальші письмові інструкції. Третій стовпець містить цифри, відповідні написаним крокам і інструкціям. У верхньому ряду перша клітина говорить: «Крок 1. Знайдіть вказане значення місця за допомогою стрілки. Всі цифри зліва не змінюються». У другій камері інструкція говорить: «Знайдіть сотні місце в 23 658». У третій осередку знаходиться цифра 23 658 зі стрілкою, що вказує на цифру 6, що позначає її «сотні місце».На один ряд вниз, інструкція в першій клітинці говорить: «Крок 2. Підкресліть цифру праворуч від заданого значення місця». У другій клітинці інструкція говорить: «Підкресліть 5, що знаходиться праворуч від сотні місця». У третій осередку знову є число 23 658, та ж стрілка, що вказує на цифру 6, що позначає її сотнею місця. У цій клітинці також підкреслено 5.Один ряд вниз, перша клітина говорить: «Крок 3. Ця цифра більше або дорівнює 5? Так — додайте 1 до цифри у вказаному значенні місця. Ні - не змінюйте цифру в даному місці.» У другій клітинці інструкція говорить: «Додайте 1 до 6 на місці сотні, так як 5 більше або дорівнює 5». Третя осередок знову містить число 23 658, зі стрілкою, що вказує на цифру 6 і текстом «додати 1». Також є фігурна дужка під цифрами 5 і 8, з вказаною на них стрілкою і текстом «замінити на 0s».У нижньому ряду перша клітинка говорить: «Крок 4. Замініть всі цифри праворуч від заданого значення місця нулями. Так, 23 700 округлені до найближчої сотні». У другій осередку в інструкції написано: «Замініть всі цифри праворуч від сотні місце нулями». Третя осередок містить число 23 700, якого ми досягли, округливши число 23 658 до найближчої сотні.

    Вправа\(\PageIndex{11}\)

    Округлення до найближчої сотні: 17,852.

    Відповідь

    17 900

    Вправа\(\PageIndex{12}\)

    Округлення до найближчої сотні: 468 751.

    Відповідь

    468 800

    ОКРУГЛИТИ ЦІЛІ ЧИСЛА.
    1. Знайдіть задане значення місця і позначте його стрілкою. Всі цифри зліва від стрілки не змінюються.
    2. Підкресліть цифру праворуч від заданого значення місця.
    3. Ця цифра більше або дорівнює 5?
      • Так - додайте 11 до цифри у вказаному значенні місця.
      • Ні — не змінюйте цифру в даному місці.
    4. Замініть всі цифри праворуч від заданого значення місця нулями.
    Вправа\(\PageIndex{13}\)

    Округлити 103,978103,978 до найближчого:

    1. сотня
    2. тисяча
    3. десять тисяч
    Відповідь
    1.
    Знайдіть сотні місце в 103 978. .
    Підкресліть цифру праворуч від місця сотні. .
    Оскільки 7 більше або дорівнює 5, додайте 1 до 9. Замініть всі цифри праворуч від місця сотні нулями. .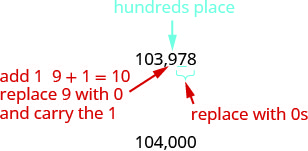
      Так, 104 000 - це 103 978 округлених до найближчої сотні.
    2.
    Знайдіть тисячі місць і підкреслюйте цифру праворуч від тисячі місць. .
    Оскільки 9 більше або дорівнює 5, додайте 1 до 3. Замініть всі цифри праворуч від місця сотні нулями. .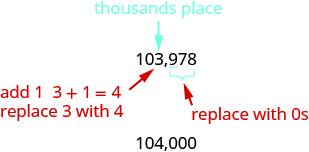
      Так, 104 000 - це 103 978 округлено до найближчої тисячі.
    3.
    Знайдіть місце в десяти тисячах і підкреслюйте цифру праворуч від десяти тисяч місця. .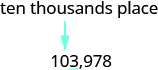
    Оскільки 3 менше 5, залишаємо 0 як є, а потім замінюємо цифри праворуч нулями. .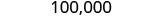
      Так, 100 000 - це 103 978 округлено до найближчих десяти тисяч.
    Вправа\(\PageIndex{14}\)

    Навколо 206 981 до найближчого: 1. сотня 2. тис. 3. десять тис.

    Відповідь
    1. 207 000
    2. 207 000
    3. 210 000
    Вправа\(\PageIndex{15}\)

    Раунд 784,951 до найближчого: 1. сотня 2. тис. 3. десять тисяч.

    Відповідь
    1. 785 000
    2. 785 000
    3. 780 000

    Визначте кратні та застосуйте тести на подільність

    Числа 2, 4, 6, 8, 10 і 12 називаються кратними 2. Кратне 2 може бути записано як добуток рахункового числа і 2.

    Діаграма, що складається з двох рядків чисел. У верхньому ряду написано «2, 4, 6, 8, 10, 12», а потім еліпсис. Нижче 2 - 2 рази 1, нижче 4 - 2 рази 2, нижче 6 - 2 рази 3, нижче 8 - 2 рази 4, нижче 10 - 2 рази 5, а нижче 12 - 2 рази 6.
    Малюнок\(\PageIndex{4}\)

    Аналогічно, кратне 3 буде добутком числа підрахунку і 3.

    Діаграма, що складається з двох рядків чисел. У верхньому ряду написано «3, 6, 9, 12, 15, 18», а потім еліпсис. Нижче 3 - 3 рази 1, нижче 6 - 3 рази 2, нижче 9 - 3 рази 3, нижче 12 - 3 рази 4, нижче 15 - 3 рази 5, а нижче 18 - 3 рази 6.
    Малюнок\(\PageIndex{5}\)

    Ми могли б знайти кратні будь-якому числу, продовжуючи цей процес.

    Примітка

    Виконання діяльності з маніпулятивної математики «Кратні» допоможе вам розвинути краще розуміння кратних.

    Таблиця\(\PageIndex{1}\) показує кратні від 2 до 9 для перших 12 підрахункових чисел.

    Кількість підрахунку 1 2 3 4 5 6 7 8 9 10 11 12
    Кратні 2 2 4 6 8 10 12 14 16 18 20 22 24
    Кратні 3 3 6 9 12 15 18 21 24 27 30 33 36
    Кратні 4 4 8 12 16 20 24 28 32 36 40 44 48
    Кратні 5 5 10 15 20 25 30 35 40 45 50 55 60
    Кратні 6 6 12 18 24 30 36 42 48 54 60 66 72
    Кратні 7 7 14 21 28 35 42 49 56 63 70 77 84
    Кратні 8 8 16 24 32 40 48 56 64 72 80 88 96
    Кратні 9 9 18 27 36 45 54 63 72 81 90 99 108
    Кратні 10 10 20 30 40 50 60 70 80 90 100 110 120
    Таблиця\(\PageIndex{1}\)
    КРАТНА ЧИСЛУ

    Число кратне,\(n\) якщо воно є добутком лічильного числа і\(n\).

    Інший спосіб сказати, що 15 кратний 3 - це сказати, що 15 ділиться на 3. Це означає, що коли ми ділимо 3 на 15, ми отримуємо лічильне число. Насправді,\(15\div 3\) це 5, тому 15 є\(5\cdot3\).

    ДІЛИТЬСЯ НА ЧИСЛО

    Якщо число\(m\) кратне\(n\),\(m\) то ділиться на\(n\)

    Подивіться на кратні\(5\) в табл\(\PageIndex{1}\). Всі вони закінчуються на 5 або 0. Числа з останньою цифрою 5 або 0 діляться на 5. Шукаючи інші закономірності в таблиці\(\PageIndex{1}\), яка показує кратні числам від 2 до 9, ми можемо виявити наступні тести на подільність:

    ТЕСТИ НА ПОДІЛЬНІСТЬ

    Число ділиться на:

    • 2, якщо остання цифра дорівнює 0, 2, 4, 6 або 8.
    • 3, якщо сума цифр ділиться на 3.
    • 5, якщо остання цифра дорівнює 5 або 0.
    • 6, якщо він ділиться як на 2, так і на 3.
    • 10, якщо він закінчується на 0.
    Вправа\(\PageIndex{16}\)

    5625 ділиться на 2? За 3? До 5? До 6? До 10?

    Відповідь

    \[\begin{array} {ll} {\text{Is 5625 divisible by 2?}} &{} \\ {\text{Does it end in 0, 2, 4, 6, or 8?}} &{\text{No.}} \\ {} &{\text{5625 is not divisible by 2.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 3?}} &{} \\ {\text{What is the sum of the digits?}} &{5 + 6 + 2 + 5 = 18} \\ {\text{Is the sum divisible by 3?}} &{\text{Yes, 5625 is divisible by 3.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 5 or 10?}} &{} \\ {\text{What is the last digit? It is 5.}} &{\text{5625 is divisible by 5 but not by 10.}} \end{array}\]

    \[\begin{array} {ll} {\text{Is 5625 divisible by 6?}} &{} \\ {\text{Is it divisible by both 2 and 3?}} &{\text{No, 5625 is not divisible by 2, so 5625 is }} \\ {} &{\text{not divisible by 6.}}\end{array}\]

    Вправа\(\PageIndex{17}\)

    Визначте, чи 4 962 ділиться на 2, на 3, на 5, на 6 і на 10.

    Відповідь

    на 2, 3 і 6

    Вправа\(\PageIndex{18}\)

    Визначте, чи ділиться 3,765 на 2, на 3, на 5, на 6, і на 10.

    Відповідь

    на 3 і 5

    Пошук простих факторизацій та найменш поширених кратних

    У математиці часто існує кілька способів говорити про одні й ті ж ідеї. Поки що ми бачили, що якщо\(m\) є кратним\(n\), ми можемо сказати,\(m\) що ділиться на\(n\). Наприклад, оскільки 72 кратна 8, ми говоримо, що 72 ділиться на 8. Оскільки 72 кратна 9, ми говоримо, що 72 ділиться на 9. Ми можемо висловити це ще іншим способом.

    Так як\(8\cdot 9=72\), ми говоримо, що 8 і 9 - фактори 72. Коли ми пишемо\(72=8\cdot 9\), ми говоримо, що ми враховували 72.

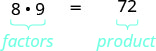
    На зображенні показано рівняння 8 разів 9 дорівнює 72. Написано під виразом 8 разів 9 є фігурною дужкою, а слово «фактори», написане нижче 72, є горизонтальною дужкою та словом «продукт».
    Малюнок\(\PageIndex{6}\)

    Інші способи фактора 72 є\(1\cdot 72\),\(2\cdot 36\),\(3\cdot 24\),\(4\cdot 18\) і\(6\cdot 12\). Сімдесят два мають багато факторів: 1, 2, 3, 4, 6, 8, 9, 12, 18, 36 і 72.

    ФАКТОРИ

    Якщо\(a\cdot b=m\), то\(a\) і\(b\) є чинниками\(m\).

    Деякі цифри, як 72, мають багато факторів. Інші числа мають лише два фактори.

    Примітка

    Виконання діяльності з маніпулятивної математики «Модельне множення та факторинг» допоможе вам краще зрозуміти множення та факторинг.

    ПРОСТЕ ЧИСЛО ТА СКЛАДЕНЕ ЧИСЛО

    Просте число - це лічильне число більше 1, чиї єдиними факторами є 1 і саме по собі.

    Складене число - це лічильне число, яке не є простим. Складене число має фактори, відмінні від 1 і самого себе.

    Примітка

    Виконання діяльності з маніпулятивної математики «Прості числа» допоможе вам розвинути краще розуміння простих чисел.

    Числа підрахунку від 2 до 19 наведені на малюнку\(\PageIndex{7}\), з їх коефіцієнтами. Обов'язково погоджуйтеся з «основним» або «складовим» етикеткою для кожного!

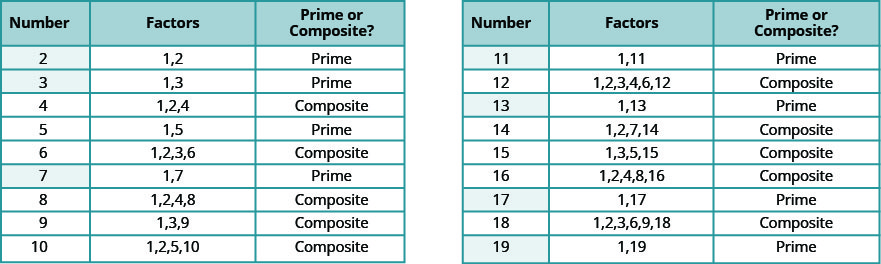
    Таблиця показана з одинадцятьма рядками та сімома стовпцями. Перший рядок є рядком заголовка, і кожна комірка позначає вміст стовпця під ним. У рядку заголовка перші три клітинки читаються зліва направо «Число», «Фактори» та «Просте чи складене?» Весь четвертий стовпець порожній. Останні три клітинки читають зліва направо «Число», «Фактор» та «Просте чи складене?» знову. У кожному наступному рядку перша комірка містить число, друга містить його множники, а третя вказує, чи є число простим або складеним. Три стовпці зліва від порожнього середнього стовпця містять цю інформацію для числа від 2 до 10, а три стовпці праворуч від порожнього середнього стовпця містять цю інформацію для числа від 11 до 19. У лівій частині порожнього стовпця, у першому рядку під рядком заголовка, клітинки читаються зліва направо: «2», «1,2» та «Prime». У наступному рядку клітини читають зліва направо: «3», «1,3» і «Prime». У наступному рядку клітинки читають зліва направо: «4», «1,2,4» і «Складене». У наступному ряду осередки читають зліва направо: «5», «1,5» і «Prime». У наступному ряду осередки читають зліва направо: «6», «1,2,3,6» і «Складові». У наступному ряду осередки читають зліва направо: «7», «1,7», і «Prime». У наступному рядку клітинки читають зліва направо: «8», «1,2,4,8» і «Композит». У наступному рядку клітинки читають зліва направо: «9», «1,3,9» і «Складене». У нижньому ряду осередки читаються зліва направо: «10», «1,2,5,10» та «Композитний». У правій частині порожнього стовпця, у першому рядку під рядком заголовка, клітинки читаються зліва направо: «11», «1,11» та «Prime». У наступному рядку клітинки читають зліва направо: «12», «1,2,3,4,6,12», і «Складові». У наступному ряду осередки читають зліва направо: «13», «1,13» і «Prime». У наступному рядку клітинки читають зліва направо «14», «1,2,7,14» та «Композитний». У наступному рядку клітинки читають зліва направо: «15», «1,3,5,15» і «Композитний». У наступному рядку клітинки читають зліва направо: «16», «1,2,4,8,16» і «Композитний». У наступному ряду осередки читаються зліва направо, «17», «1,17» і «Prime». У наступному рядку клітинки читаються зліва направо, «18», «1,2,3,6,9,18» та «Композитний». У нижньому ряду осередки читаються зліва направо: «19», «1,19» і «Prime».
    Малюнок\(\PageIndex{7}\)

    Просте число s менше 20 - 2, 3, 5, 7, 11, 13, 17 та 19. Зверніть увагу, що єдине парне просте число - 2.

    Складене число можна записати як унікальний твір простих чисел. Це називається простим факторизацією числа. Знаходження простої факторизації складеного числа буде корисно пізніше в цьому курсі.

    ОСНОВНА ФАКТОРИЗАЦІЯ

    Просте факторизація числа - це добуток простих чисел, що дорівнює числу.

    Щоб знайти просту факторизацію складеного числа, знайдіть будь-які два множники числа і використовуйте їх для створення двох гілок. Якщо коефіцієнт є простим, ця гілка завершена. Коло, що прем'єр!

    Якщо коефіцієнт не простий, знайдіть два множника числа і продовжуйте процес. Після того, як всі гілки обвели прості числа в кінці, факторизація завершена. Складене число тепер можна записати як добуток простих чисел.

    Вправа\(\PageIndex{19}\)

    Фактор 48.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Другий стовпець містить подальші письмові інструкції та деякі математики. Третій стовпець містить більшу частину математичної роботи, що відповідає написаним крокам та інструкціям. У верхньому ряду перша клітина говорить: «Крок 1. Знайдіть два фактори, твором яких є задане число. Використовуйте ці цифри, щоб створити дві гілки». Друга комірка містить алгебраїчне рівняння 48, рівне 2 рази 24. У третій клітинці є факторне дерево з 48 вгорі. Дві гілки спускаються з 48 і закінчуються на 2 і 24 відповідно.На один ряд вниз, інструкція в першій клітинці говорить: «Крок 2. Якщо коефіцієнт є простим, ця гілка завершена. Обведіть просте». У другій клітинці інструкція говорить: «2 - просте. Обведіть просте». У третій клітинці дерево факторів з кроку 1 повторюється, але 2 внизу дерева тепер обводиться.Один ряд вниз, перша клітина говорить: «Крок 3. Якщо фактор не є простим, запишіть його як добуток двох факторів і продовжуйте процес». У другій клітинці інструкція говорить: «24 не є простими. Розбийте його ще на 2 фактори». Третя комірка містить початкове дерево факторів, з 48 у верхній частині та двома спрямованими вниз гілками, що закінчуються на 2, що підкреслено, і 24. Ще дві гілки спускаються з 24 і закінчуються на 4 і 6 відповідно. Один рядок вниз, інструкції в середині комірки кажуть, що «4 і 6 не є простими. Розбийте їх кожен на два фактори». У клітинці праворуч дерево факторів повторюється ще раз. Дві гілки спускаються з 4 і закінчуються на 2 і 2. Обидва 2s обведені по колу. Ще дві гілки спускаються з 6 і закінчуються на 2 і 3, які обидва обведені. В інструкції зліва написано «2 і 3 прості, тому обведіть їх».У нижньому ряду перша клітинка говорить: «Крок 4. Запишіть складене число як добуток усіх обведених простих чисел». Другу клітинку залишаємо порожньою. Третя комірка містить алгебраїчне рівняння 48, рівне 2 рази 2 рази 2 рази 2 рази 3.

    Ми говоримо\(2\cdot 2\cdot 2\cdot 2\cdot 3\), що це основна факторизація 48. Ми зазвичай пишемо прості числа в порядку зростання. Обов'язково помножте фактори, щоб перевірити свою відповідь!

    Якби ми спочатку враховували 48 по-іншому, наприклад, як\(6\cdot 8\), результат все одно був би таким же. Закінчіть основну факторизацію і переконайтеся в цьому самі.

    Вправа\(\PageIndex{20}\)

    Знайдіть просте факторизацію 80.

    Відповідь

    \(2\cdot 2\cdot 2\cdot 2\cdot 5\)

    Вправа\(\PageIndex{21}\)

    Знайдіть просте факторизацію 60.

    Відповідь

    \(2\cdot 2\cdot 3\cdot 5\)

    ЗНАЙДІТЬ ПРОСТЕ ФАКТОРИЗАЦІЮ СКЛАДЕНОГО ЧИСЛА.
    1. Знайдіть два фактори, твором яких є задане число, і використовуйте ці числа для створення двох гілок.
    2. Якщо коефіцієнт є простим, ця гілка завершена. Обведіть прайм, як бутон на дереві.
    3. Якщо коефіцієнт не є простим, запишіть його як добуток двох факторів і продовжуйте процес.
    4. Запишіть складене число як добуток всіх обведених простих чисел.
    Вправа\(\PageIndex{22}\)

    Знайдіть просте факторизацію 252.

    Відповідь
    Крок 1. Знайдіть два фактори, твір яких дорівнює 252. 12 і 21 не є простими.

    Розбийте 12 і 21 ще на два фактори. Продовжуйте до тих пір, поки не будуть враховані всі прості числа.    		 .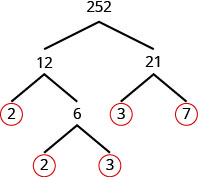
    Крок 2. Запишіть 252 як добуток всіх обведених простих чисел.

    \(252=2\cdot 2\cdot 3\cdot 3\cdot 7\)
    Вправа\(\PageIndex{23}\)

    Знайдіть просте факторизацію 126.

    Відповідь

    \(2\cdot 3\cdot 3\cdot 7\)

    Вправа\(\PageIndex{24}\)

    Знайдіть просте факторизацію 294.

    Відповідь

    \(2\cdot 3\cdot 7\cdot 7\)

    Однією з причин, чому ми розглядаємо кратні та прості числа, є використання цих методів, щоб знайти найменш поширене кратне двох чисел. Це буде корисно, коли ми додаємо і віднімаємо дроби з різними знаменниками s. Два методи використовуються найчастіше для пошуку найменш спільного кратного, і ми розглянемо обидва з них.

    Перший метод - це метод лістингу кратних. Щоб знайти найменш поширене кратне 12 і 18, ми перерахуємо перші кілька кратних 12 і 18:

    Буде показано два рядки чисел. Перший ряд починається з 12, за ним слід двокрапка, потім 12, 24, 36, 48, 60, 72, 84, 96, 108 і еліпсіс. 36, 72 і 108 жирним шрифтом пишуться червоним шрифтом. Другий ряд починається з 18, за ним слід двокрапка, потім 18, 36, 54, 72, 90, 108, і еліпсис. Знову ж таки, цифри 36, 72 і 108 жирним шрифтом написані червоним шрифтом. На рядку нижче словосполучення «Загальні кратні», двокрапка і цифри 36, 72 і 108, написані червоним кольором. Один рядок нижче - словосполучення «Найменше загальне кратне», двокрапка і цифра 36, написана синім кольором.
    Малюнок\(\PageIndex{8}\)

    Зверніть увагу, що деякі цифри відображаються в обох списках. Вони є загальними кратними 12 і 18.

    Ми бачимо, що перші кілька загальних кратних 12 і 18 36, 72 і 108. Оскільки 36 є найменшим із загальних кратних, ми називаємо його найменш загальним кратним. Ми часто використовуємо абревіатуру LCM.

    НАЙМЕНШ ЗАГАЛЬНЕ КРАТНЕ

    Найменш поширене кратне (НСМ) двох чисел - це найменше число, кратне обом числам.

    У вікні процедури наведено кроки, які потрібно зробити, щоб знайти LCM за допомогою методу простих факторів, який ми використовували вище для 12 та 18.

    ЗНАЙДІТЬ НАЙМЕНШ ПОШИРЕНЕ КРАТНЕ, ПЕРЕРАХОВУЮЧИ КРАТНІ.
    1. Перерахуйте кілька кратних кожному числу.
    2. Шукайте найменшу цифру, яка відображається в обох списках.
    3. Це число і є НКМ.
    Вправа\(\PageIndex{25}\)

    Знайдіть найменш поширене кратне 15 і 20, перерахувавши кратні.

    Відповідь
    Складіть списки перших кількох кратних 15 і 20, і використовуйте їх, щоб знайти найменш поширене кратне. .
    Шукайте найменшу цифру, яка відображається в обох списках. Перше число, яке з'явиться в обох списках, - 60, тому 60 є найменш поширеним кратним 15 і 20.

    Зверніть увагу, що 120 є в обох списках, теж. Це загальне кратне, але це не найменш поширене множинне.

    Вправа\(\PageIndex{26}\)

    Знайдіть найменш поширене кратне, перерахувавши кратні: 9 та 12.

    Відповідь

    \(36\)

    Вправа\(\PageIndex{27}\)

    Знайдіть найменш поширене кратне, перерахувавши кратні: 18 і 24.

    Відповідь

    \(72\)

    Наш другий метод пошуку найменш поширених кратних двох чисел полягає у використанні методу простих факторів. Давайте знову знайдемо LCM 12 і 18, на цей раз використовуючи їх прості множники.

    Вправа\(\PageIndex{28}\)

    Знайдіть найменше спільне кратне (НКМ) 12 та 18 за допомогою методу простих факторів.

    Відповідь

    Ця цифра являє собою таблицю, яка має три стовпці і чотири рядки. Перший стовпець є стовпцем заголовка, і він містить імена та номери кожного кроку. Другий стовпець містить подальші письмові інструкції та деякі математики. Третій стовпець містить більшу частину математичної роботи, що відповідає написаним крокам та інструкціям. У верхньому ряду перша клітина говорить: «Крок 1. Запишіть кожне число як добуток простих чисел». Другу клітинку залишаємо порожньою. У третій клітці є два факторних дерева. У дереві першого множника дві гілки спускаються з 18 і закінчуються на 3 і 6 відповідно. 3 є простим і, отже, обведено. Ще дві гілки спускаються з 6 і закінчуються в 2 і 3, обидві з яких обведені. У другому факторному дереві дві гілки спускаються з 12 і закінчуються на 3 і 4. 3 обводиться по колу. Ще дві гілки спускаються з 4, закінчуючись на 2 і 2, обидві з яких обведені.На один ряд вниз, інструкція в першій клітинці говорить: «Крок 2. Перерахуйте прості числа кожного числа. Зіставте прості числа вертикально, коли це можливо». У другій клітинці інструкція говорить: «Перерахуйте прості числа 12. Перерахуйте прості числа 18. Вибудовуйтеся з простими числами 12, коли це можливо. Якщо немає, створіть новий стовпець.» Третя комірка містить просту факторизацію 12, записану як рівняння 12 дорівнює 2 рази 2 рази 3. Нижче цього рівняння знаходиться ще одне, що показує просту факторизацію 18, записану як рівняння 18 дорівнює 2 рази 3 рази 3. Два рівняння вирівнюються вертикально на рівному символі. Перші 2 в простому факторизації 12 вирівнюється з 2 в простому факторизації 18. Під другою 2 в простій факторизації 12 знаходиться розрив у простому факторизації 18. Під 3 в простому факторизації 12 є перші 3 в простому факторизації 18. Другий 3 у простій факторизації не має факторів над ним від простої факторизації 12.Одним рядком вниз, в інструкції в першій клітинці написано: «Збийте число з кожного стовпця». Друга осередок порожня. Третя комірка містить прості множники 12 і 18 знову, проілюстровані як два рівняння, вирівняні так само, як вони були раніше. На цей раз проводиться горизонтальна лінія під просту факторизацію 18. Нижче цього рядка знаходиться рівняння LCM, рівне 2 рази 2 рази 3 рази. Стрілки намальовані вниз вертикально від простої факторизації 12 через просту факторизацію 18, що закінчується рівнянням LCM. Перша стрілка починається з перших 2 у простому факторизації 12 і продовжується вниз через 2 в простій факторизації 18, закінчуючи першими 2 в LCM. Друга стрілка починається з наступної 2 в простій факторизації 12 і триває вниз через прогалину в простій факторизації 18, закінчуючи другою 2 в НКМ. Третя стрілка починається з 3 в простому факторизації 12 і триває вниз через перші 3 в простому факторизації 18, закінчуючи першими 3 в LCM. Остання стрілка починається з другої 3 в простій факторизації 18 і вказує вниз до другої 3 в LCM.У нижньому рядку таблиці перша комірка говорить: «Крок 4: Множимо множники». Друга осередок - банк. Третя комірка містить рівняння LCM дорівнює 36.

    Зверніть увагу, що прості\(12(2\cdot 2\cdot 3)\) множники і прості множники\(18(2\cdot 3\cdot 3)\) включені в НКМ\((2\cdot 2\cdot 3\cdot 3)\). Таким чином, 36 є найменш поширеним кратним 12 і 18.

    При зіставленні загальних простих чисел кожен загальний простий коефіцієнт використовується лише один раз. Таким чином ви впевнені, що 36 є найменш поширеним кратним.

    Вправа\(\PageIndex{29}\)

    Знайти LCM за допомогою методу простих множників: 9 і 12.

    Відповідь

    \(36\)

    Вправа\(\PageIndex{30}\)

    Знайдіть LCM за допомогою методу простих множників: 18 і 24.

    Відповідь

    \(72\)

    ЗНАЙДІТЬ НАЙМЕНШ ЗАГАЛЬНЕ КРАТНЕ ЗА ДОПОМОГОЮ МЕТОДУ ПРОСТИХ ФАКТОРІВ.
    1. Запишіть кожне число як добуток простих чисел.
    2. Перерахуйте прості числа кожного числа. Зіставте прості числа вертикально, коли це можливо.
    3. Збийте колони.
    4. Помножте коефіцієнти.
    Вправа\(\PageIndex{31}\)

    Знайдіть найменш спільне кратне (НКМ) 24 та 36 за допомогою методу простих факторів.

    Відповідь
    Знайдіть прості числа 24 і 36.
    Зіставте прості числа вертикально, коли це можливо.

    Збиваємо всі стовпчики.    		 .
    Помножте коефіцієнти. .
     

    НКМ 24 і 36 дорівнює 72.
    Вправа\(\PageIndex{32}\)

    Знайти LCM за допомогою методу простих множників: 21 і 28.

    Відповідь

    \(84\)

    Вправа\(\PageIndex{33}\)

    Знайдіть LCM за допомогою методу простих множників: 24 і 32.

    Відповідь

    \(96\)

    Примітка

    Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з використанням цілих чисел. Вам потрібно буде включити Java у вашому веб-браузері, щоб використовувати додаток.

    Ключові поняття

    • Значення місця, як на малюнку.
    • Назвіть ціле число у словах
      1. Почніть ліворуч і назвіть номер у кожному періоді, а потім назву періоду.
      2. Поставте коми в число, щоб відокремити періоди.
      3. Не називайте ті період.
    • Напишіть ціле число, використовуючи цифри
      1. Визначте слова, які вказують на періоди. (Пам'ятайте, що ті період ніколи не названий.)
      2. Намалюйте 3 заготовки, щоб вказати кількість місць, необхідних в кожному періоді. Розділіть періоди комами.
      3. Назвіть номер у кожному періоді та розмістіть цифри у правильній позиції значення місця.
    • Круглі цілі числа
      1. Знайдіть задане значення місця і позначте його стрілкою. Всі цифри зліва від стрілки не змінюються.
      2. Підкресліть цифру праворуч від заданого значення місця.
      3. Ця цифра більше або дорівнює 5?
        • Так — додайте 1 до цифри у вказаному значенні місця.
        • Ні — не змінюйте цифру в даному місці.
      4. Замініть всі цифри праворуч від заданого значення місця нулями.
    • Тести на подільність: Число ділиться на:
      • 2, якщо остання цифра дорівнює 0, 2, 4, 6 або 8.
      • 3, якщо сума цифр ділиться на 3.
      • 5, якщо остання цифра дорівнює 5 або 0.
      • 6, якщо він ділиться як на 2, так і на 3.
      • 10, якщо він закінчується на 0.
    • Знайти просту факторизацію складеного числа
      1. Знайдіть два фактори, твором яких є задане число, і використовуйте ці числа для створення двох гілок.
      2. Якщо коефіцієнт є простим, ця гілка завершена. Обведіть прайм, як бутон на дереві.
      3. Якщо коефіцієнт не є простим, запишіть його як добуток двох факторів і продовжуйте процес.
      4. Запишіть складене число як добуток всіх обведених простих чисел.
    • Знайдіть найменш поширене кратне, перерахувавши кратні
      1. Перерахуйте кілька кратних кожному числу.
      2. Шукайте найменшу цифру, яка відображається в обох списках.
      3. Це число і є НКМ.
    • Знайдіть найменш поширене кратне за допомогою методу простих факторів
      1. Запишіть кожне число як добуток простих чисел.
      2. Перерахуйте прості числа кожного числа. Зіставте прості числа вертикально, коли це можливо.
      3. Збийте колони.
      4. Помножте коефіцієнти.

    Глосарій

    складене число
    Складене число - це лічильне число, яке не є простим. Складене число має фактори, відмінні від 1 і самого себе.
    підрахунок чисел
    Підрахувальні числа - це цифри 1, 2, 3,...
    ділиться на число
    Якщо число\(m\) кратне\(n\), то\(m\) ділиться на\(n\). (Якщо 6 кратна 3, то 6 ділиться на 3.)
    фактори
    Якщо\(a\cdot b=m\), то\(a\) і\(b\) є чинниками\(m\). Так як\(3 \cdot 4 = 12\), то 3 і 4 - фактори 12.
    найменш поширене кратне
    Найменш поширене кратне двох чисел - це найменше число, кратне обом числам.
    кратне числу
    Число кратне,\(n\) якщо воно є добутком лічильного числа і\(n\).
    номер рядка
    Числовий рядок використовується для візуалізації чисел. Числа на числовому рядку стають більшими, оскільки вони йдуть зліва направо, і менше, коли вони йдуть справа наліво.
    походження
    Походження - це точка з позначкою 0 на числовому рядку.
    основна факторизація
    Просте факторизація числа - це добуток простих чисел, що дорівнює числу.
    просте число
    Просте число - це лічильне число більше 1, єдиними факторами якого є 1 і саме по собі.
    цілих чисел
    Цілими числами є числа 0, 1, 2, 3,...