Глава 1 Огляд вправ
- Page ID
- 59040
Розділ Огляд Вправи
Вступ до цілих чисел
Використовувати значення місця з цілим числом
У наступних вправах знайдіть місце значення кожної цифри.
26 915
- 1
- 2
- 9
- 5
- 6
- Відповідь
-
- десятки
- десять тисяч
- сотні
- одиничні
- тисячі
359 417
- 9
- 3
- 4
- 7
- 1
58 129 304
- 5
- 0
- 1
- 8
- 2
- Відповідь
-
- десять мільйонів
- десятки
- сто тисяч
- мільйони
- десять тисяч
9 430 286 157
- 6
- 4
- 9
- 0
- 5
У наступних вправах назвіть кожне число.
6 104
- Відповідь
-
шість тисяч, сто чотири
493 068
3 975 284
- Відповідь
-
три мільйони дев'ятсот сімдесят п'ять тисяч двісті вісімдесят чотири
85 620 435
У наступних вправах запишіть кожне число як ціле число, використовуючи цифри.
триста п'ятнадцять
- Відповідь
-
315
шістдесят п'ять тисяч дев'ятсот дванадцять
дев'яносто мільйонів, чотириста двадцять п'ять тисяч шістнадцять
- Відповідь
-
90 425 016
один мільярд сорок три мільйони дев'ятсот двадцять дві тисячі триста одинадцять
У наступних вправах округляйте до зазначеного значення місця.
Округлити до найближчої десяти.
- 407
- 8 564
- Відповідь
-
- 410
- 8 560
Округлити до найближчої сотні.
- 25 846
- 25 864
У наступних вправах округляйте кожне число до найближчого 1. сотня 2. тисячі 3. десять тисяч.
864 951
- Відповідь
-
- 865 000865 000
- 865 000865 000
- 860 000
3 972 849
Визначте кратні та коефіцієнти
У наступних вправах використовуйте тести на подільність, щоб визначити, чи ділиться кожне число на 2, на 3, на 5, на 6 та на 10.
168
- Відповідь
-
від 2,3,6
264
375
- Відповідь
-
на 3,5
750
1430
- Відповідь
-
від 2,5,10
1080
Пошук простих факторизацій та найменш поширених кратних
У наступних вправах знайдіть просту факторизацію.
420
- Відповідь
-
2\(\cdot 2 \cdot 3 \cdot 5 \cdot 7\)
115
225
- Відповідь
-
3\(\cdot 3 \cdot 5 \cdot 5\)
2475
1560
- Відповідь
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 5 \cdot 13\)
56
72
- Відповідь
-
\(2 \cdot 2 \cdot 2 \cdot 3 \cdot 3\)
168
252
- Відповідь
-
\(2 \cdot 2 \cdot 3 \cdot 3 \cdot 7\)
391
У наступних вправах знайдіть найменш поширене кратне з наступних чисел за допомогою методу multiples.
6,15
- Відповідь
-
30
60, 75
У наступних вправах знайдіть найменш поширене кратне з наступних чисел за допомогою методу простих факторів.
24, 30
- Відповідь
-
120
70, 84
Використання мови алгебри
Використання змінних та алгебраїчних символів
У наступних вправах перекладіть наступне з алгебри на англійську мову.
25−7
- Відповідь
-
25 мінус 7, різниця двадцять п'ять і сім
5\(\cdot 6\)
\(45 \div 5\)
- Відповідь
-
45 ділиться на 5, частка сорок п'ять і п'ять
х+8
\(42 \geq 27\)
- Відповідь
-
сорок два більше або дорівнює двадцяти семи
3н=24
\(3 \leq 20 \div 4\)
- Відповідь
-
3 менше або дорівнює 20 ділиться на 4, три менше або дорівнює частці двадцяти і чотирьох
\(a \neq 7 \cdot 4\)
У наступних вправах визначте, чи є кожне виразом чи рівнянням.
\(6 \cdot 3+5\)
- Відповідь
-
вираз
y−8=32
Спрощення виразів за допомогою порядку операцій
У наступних вправах спрощуйте кожен вираз.
\(3^{5}\)
- Відповідь
-
243
\(10^{8}\)
У наступних вправах спростіть
6+10/2+2
- Відповідь
-
13
9+12/3+4
\(20 \div(4+6) \cdot 5\)
- Відповідь
-
10
\(33 \div(3+8) \cdot 2\)
\(4^{2}+5^{2}\)
- Відповідь
-
41
\((4+5)^{2}\)
Оцінити вираз
У наступних вправах оцініть наступні вирази.
9х+7 при х=3
- Відповідь
-
34
5x−4, коли x=6
\(x^{4}\)коли\(x=3\)
- Відповідь
-
81
\(3^{x}\)коли\(x=3\)
\(x^{2}+5 x-8\)коли\(x=6\)
- Відповідь
-
58
\(2 x+4 y-5\)коли
\(x=7, y=8\)
Спростіть вирази, поєднуючи подібні терміни
У наступних вправах визначте коефіцієнт кожного члена.
12н
- Відповідь
-
12
9\(x^{2}\)
У наступних вправах виділіть подібні терміни.
\(3 n, n^{2}, 12,12 p^{2}, 3,3 n^{2}\)
- Відповідь
-
12\(3, n^{2}\) і 3\(n^{2}\)
\(5,18 r^{2}, 9 s, 9 r, 5 r^{2}, 5 s\)
У наступних вправах визначте терміни в кожному виразі.
\(11 x^{2}+3 x+6\)
- Відповідь
-
\(11 x^{2}, 3 x, 6\)
\(22 y^{3}+y+15\)
У наступних вправах спростіть наступні вирази, комбінуючи подібні терміни.
17а+9а
- Відповідь
-
26а
18 з+9
9х+3х+8
- Відповідь
-
12х+8
8а+5а+9
7п+6+5п−4
- Відповідь
-
12п+2
8х+7+4х−5
Перекласти англійську фразу на алгебраїчний вираз
У наступних вправах переведіть наступні фрази в алгебраїчні вирази.
сума 8 і 12
- Відповідь
-
8+12
сума 9 і 1
різниця х і 4
- Відповідь
-
x−4
різниця х і 3
твір 6 і y
- Відповідь
-
6й
твір 9 і y
Адель купила спідницю і блузку. Спідниця коштувала на 15 доларів дорожче блузки. Нехай bb представляють вартість блузки. Напишіть вираз для вартості спідниці.
- Відповідь
-
б+15
Марселла має 6 менше двоюрідних братів хлопчиків, ніж двоюрідних братів. Нехай g представляють кількість дівок-двоюрідних братів. Напишіть вираз для кількості двоюрідних братів хлопчика.
Додавання та віднімання цілих чисел
Використовувати негативи та протилежності цілих чисел
У наступних вправах замовте кожну з наступних пар чисел, використовуючи < or >.
- 6___2
- −7___4
- −9___−1
- 9___−3
- Відповідь
-
- >
- <
- <
- >
- −5___1
- −4___−9
- 6___10
- 3___−8
У наступних вправах знайдіть протилежне кожному числу.
- −8
- 1
- Відповідь
-
- 8
- −1
- −2
- 6
У наступних вправах спростити.
− (−19)
- Відповідь
-
19
− (−53)
У наступних вправах спростити.
−m, коли
- м=3
- м = −3
- Відповідь
-
- −3
- 3
−p, коли
- p=6
- p=−6
Спрощення виразів за допомогою абсолютного значення
У наступних вправах, спростити.
- |7|
- |−25|
- |0|
- Відповідь
-
- 7
- 25
- 0
- |5|
- |0|
- |−19|
У наступних вправах заповніть <, >, або = для кожної з наступних пар чисел.
- −8___|−8|
- −|−2|___−2
- Відповідь
-
- <
- =
- |−3|___−|−3|
- 4___−|−4|
У наступних вправах спростити.
|8−4|
- Відповідь
-
4
|9−6|
8 (14−2|−2|)
- Відповідь
-
80
6 (13−4|−2|)
У наступних вправах оцініть.
1. |x| коли x=−28
- Відповідь
-
- 28
- 15
- yколи y=−37
- |−z| коли z=−24
Додати цілі числа
У наступних вправах спрощуйте кожен вираз.
−200+65
- Відповідь
-
−135
−150+45
2+ (−8) +6
- Відповідь
-
0
4+ (−9) +7
140+ (−75) +67
- Відповідь
-
132
−32+24+ (−6) +10
Віднімання цілих чисел
У наступних вправах спростити.
9−3
- Відповідь
-
6
−5− (−1)
- 15−6
- 15+ (−6)
- Відповідь
-
- 9
- 9
- 12−9
- 12+ (−9)
- 8− (−9)
- 8+9
- Відповідь
-
- 17
- 17
- 4− (−4)
- 4+4
У наступних вправах спрощуйте кожен вираз.
10− (−19)
- Відповідь
-
29
11− (−18)
31−79
- Відповідь
-
−48
39−81
−31−11
- Відповідь
-
−42
−32−18
−15− (−28) +5
- Відповідь
-
18
71+ (−10) −8
−16− (−4+1) −7
- Відповідь
-
-20
−15− (−6+4) −3
Множення цілих чисел
У наступних вправах помножте.
−5 (7)
- Відповідь
-
−35
−8 (6)
−18 (−2)
- Відповідь
-
36
−10 (−6)
Розділити цілі числа
У наступних вправах розділіть.
\(-28 \div 7\)
- Відповідь
-
-4
\(56 \div(-7)\)
\(-120 \div(-20)\)
- Відповідь
-
6
\(-200 \div 25\)
Спрощення виразів цілими числами
У наступних вправах спрощуйте кожен вираз.
−8 (−2) −3 (−9)
- Відповідь
-
43
−7 (−4) −5 (−3)
\((-5)^{3}\)
- Відповідь
-
−125
\((-4)^{3}\)
\(-4 \cdot 2 \cdot 11\)
- Відповідь
-
−88
\(-5 \cdot 3 \cdot 10\)
\(-10(-4) \div(-8)\)
- Відповідь
-
-5
\(-8(-6) \div(-4)\)
31−4 (3−9)
- Відповідь
-
55
24−3 (2−10)
Оцінити змінні вирази з цілими числами
У наступних вправах оцінюйте кожен вираз.
х+8 при
- x=−26
- x=−95
- Відповідь
-
- −18
- −87
y+9 коли
- y=−29
- y=−84
Коли b=−11, оцініть:
- b+6
- −b+6
- Відповідь
-
- −5
- 17
Коли c = −9, оцініть:
- с+ (−4) с+ (−4)
- −c+ (−4)
\(p^{2}-5 p+2\)коли
\(p=-1\)
- Відповідь
-
8
\(q^{2}-2 q+9\)коли\(q=-2\)
\(6 x-5 y+15\)коли\(x=3\) і\(y=-1\)
- Відповідь
-
38
\(3 p-2 q+9\)коли\(p=8\) і\(q=-2\)
Перекласти англійські фрази на алгебраїчні вирази
У наступних вправах переведіть на алгебраїчний вираз і спростіть, якщо це можливо.
сума −4 та −17, збільшена на 32
- Відповідь
-
(−4+ (−17)) +32; 11
- різниця 15 і −7
- відняти 15 з −7
частка −45 та −9
- Відповідь
-
\(\frac{-45}{-9} ; 5\)
добуток −12 і різниця c і d
Використання цілих чисел у програмах
У наступних вправах вирішуйте.
Температура Висока температура одного дня в Майамі-Біч, штат Флорида, склала 76°. Того ж дня висока температура в Баффало, штат Нью-Йорк була -8°. Яка різниця між температурою в Майамі-Біч і температурою в Баффало?
- Відповідь
-
84 градуси
Баланс чекового рахунку Адріани становить −22 долари на її розрахунковому рахунку. Вона вносить на рахунок $301. Що таке новий баланс?
Візуалізація дробів
Знайти еквівалентні дроби
У наступних вправах знайдіть три дроби, еквівалентні заданому дробу. Покажіть свої роботи, використовуючи цифри або алгебру.
\(\frac{1}{4}\)
- Відповідь
-
\(\frac{2}{8}, \frac{3}{12}, \frac{4}{16}\)відповіді можуть відрізнятися
\(\frac{1}{3}\)
\(\frac{5}{6}\)
- Відповідь
-
\(\frac{10}{12}, \frac{15}{18}, \frac{20}{24}\)відповіді можуть відрізнятися
\(\frac{2}{7}\)
Спрощення дробів
У наступних вправах спростити.
\(\frac{7}{21}\)
- Відповідь
-
\(\frac{1}{3}\)
\(\frac{8}{24}\)
\(\frac{15}{20}\)
- Відповідь
-
\(\frac{3}{4}\)
\(\frac{12}{18}\)
\(-\frac{168}{192}\)
- Відповідь
-
\(-\frac{7}{8}\)
\(-\frac{140}{224}\)
\(\frac{11 x}{11 y}\)
- Відповідь
-
\(\frac{x}{y}\)
\(\frac{15 a}{15 b}\)
Множення дробів
У наступних вправах помножте.
\(\frac{2}{5} \cdot \frac{1}{3}\)
- Відповідь
-
\(\frac{2}{15}\)
\(\frac{1}{2} \cdot \frac{3}{8}\)
\(\frac{7}{12}\left(-\frac{8}{21}\right)\)
- Відповідь
-
\(-\frac{2}{9}\)
\(\frac{5}{12}\left(-\frac{8}{15}\right)\)
\(-28 p\left(-\frac{1}{4}\right)\)
- Відповідь
-
7п
\(-51 q\left(-\frac{1}{3}\right)\)
\(\frac{14}{5}(-15)\)
- Відповідь
-
−42
\(-1\left(-\frac{3}{8}\right)\)
Розділити дроби
У наступних вправах розділіть
\(\frac{1}{2} \div \frac{1}{4}\)
- Відповідь
-
2
\(\frac{1}{2} \div \frac{1}{8}\)
\(-\frac{4}{5} \div \frac{4}{7}\)
- Відповідь
-
\(-\frac{7}{5}\)
\(-\frac{3}{4} \div \frac{3}{5}\)
\(\frac{5}{8} \div \frac{a}{10}\)
- Відповідь
-
\(\frac{25}{4 a}\)
\(\frac{5}{6} \div \frac{c}{15}\)
\(\frac{7 p}{12} \div \frac{21 p}{8}\)
- Відповідь
-
\(\frac{2}{9}\)
\(\frac{5 q}{12} \div \frac{15 q}{8}\)
\(\frac{2}{5} \div(-10)\)
- Відповідь
-
\(-\frac{1}{25}\)
\(-18 \div-\left(\frac{9}{2}\right)\)
У наступних вправах спростити.
\(\frac{\frac{2}{3}}{\frac{8}{9}}\)
- Відповідь
-
\(\frac{3}{4}\)
\(\frac{\frac{4}{5}}{\frac{8}{15}}\)
\(\frac{-\frac{9}{10}}{3}\)
- Відповідь
-
\(-\frac{3}{10}\)
\(\frac{2}{\frac{5}{8}}\)
\(\frac{\frac{r}{5}}{\frac{s}{3}}\)
- Відповідь
-
\(\frac{3 r}{5 s}\)
\(\frac{-\frac{x}{6}}{-\frac{8}{9}}\)
Спрощення виразів, написаних за допомогою смужки дробу
У наступних вправах спростити.
\(\frac{4+11}{8}\)
- Відповідь
-
\(\frac{15}{8}\)
\(\frac{9+3}{7}\)
\(\frac{30}{7-12}\)
- Відповідь
-
-6
\(\frac{15}{4-9}\)
\(\frac{22-14}{19-13}\)
- Відповідь
-
\(\frac{4}{3}\)
\(\frac{15+9}{18+12}\)
\(\frac{5 \cdot 8}{-10}\)
- Відповідь
-
-4
\(\frac{3 \cdot 4}{-24}\)
\(\frac{15 \cdot 5-5^{2}}{2 \cdot 10}\)
- Відповідь
-
\(\frac{5}{2}\)
\(\frac{12 \cdot 9-3^{2}}{3 \cdot 18}\)
\(\frac{2+4(3)}{-3-2^{2}}\)
- Відповідь
-
-2
\(\frac{7+3(5)}{-2-3^{2}}\)
Перекладіть фрази на вирази з дробами
У наступних вправах перекладіть кожну англійську фразу в алгебраїчний вираз.
частка c і сума d і 9.
- Відповідь
-
\(\frac{c}{d+9}\)
частка різниці h і k, і −5.
Додавання та віднімання дробів
Додавання та віднімання дробів із загальним знаменником
У наступних вправах додайте.
\(\frac{4}{9}+\frac{1}{9}\)
- Відповідь
-
\(\frac{5}{9}\)
\(\frac{2}{9}+\frac{5}{9}\)
\(\frac{y}{3}+\frac{2}{3}\)
- Відповідь
-
\(\frac{y+2}{3}\)
\(\frac{7}{p}+\frac{9}{p}\)
\(-\frac{1}{8}+\left(-\frac{3}{8}\right)\)
- Відповідь
-
\(-\frac{1}{2}\)
\(-\frac{1}{8}+\left(-\frac{5}{8}\right)\)
У наступних вправах відніміть.
\(\frac{4}{5}-\frac{1}{5}\)
- Відповідь
-
\(\frac{3}{5}\)
\(\frac{4}{5}-\frac{3}{5}\)
\(\frac{y}{17}-\frac{9}{17}\)
- Відповідь
-
\(\frac{y-9}{17}\)
\(\frac{x}{19}-\frac{8}{19}\)
\(-\frac{8}{d}-\frac{3}{d}\)
- Відповідь
-
\(-\frac{11}{d}\)
\(-\frac{7}{c}-\frac{7}{c}\)
Додавання або віднімання дробів з різними знаменниками
У наступних вправах додайте або відніміть.
\(\frac{1}{3}+\frac{1}{5}\)
- Відповідь
-
\(\frac{8}{15}\)
\(\frac{1}{4}+\frac{1}{5}\)
\(\frac{1}{5}-\left(-\frac{1}{10}\right)\)
- Відповідь
-
\(\frac{3}{10}\)
\(\frac{1}{2}-\left(-\frac{1}{6}\right)\)
\(\frac{2}{3}+\frac{3}{4}\)
- Відповідь
-
\(\frac{17}{12}\)
\(\frac{3}{4}+\frac{2}{5}\)
\(\frac{11}{12}-\frac{3}{8}\)
- Відповідь
-
\(\frac{13}{24}\)
\(\frac{5}{8}-\frac{7}{12}\)
\(-\frac{9}{16}-\left(-\frac{4}{5}\right)\)
- Відповідь
-
\(\frac{19}{80}\)
\(-\frac{7}{20}-\left(-\frac{5}{8}\right)\)
\(1+\frac{5}{6}\)
- Відповідь
-
\(\frac{11}{6}\)
\(1-\frac{5}{9}\)
Використовуйте порядок операцій для спрощення складних дробів
У наступних вправах спростити.
\(\frac{\left(\frac{1}{5}\right)^{2}}{2+3^{2}}\)
- Відповідь
-
\(\frac{1}{275}\)
\(\frac{\left(\frac{1}{3}\right)^{2}}{5+2^{2}}\)
\(\frac{\frac{2}{3}+\frac{1}{2}}{\frac{3}{4}-\frac{2}{3}}\)
- Відповідь
-
14
\(\frac{\frac{3}{4}+\frac{1}{2}}{\frac{5}{6}-\frac{2}{3}}\)
Оцінити змінні вирази за допомогою дробів
У наступних вправах оцініть.
\(x+\frac{1}{2}\)коли
- \(x=-\frac{1}{8}\)
- \(x=-\frac{1}{2}\)
- Відповідь
-
- \(\frac{3}{8}\)
- \(0\)
\(x+\frac{2}{3}\)коли
- \(x=-\frac{1}{6}\)
- \(x=-\frac{5}{3}\)
4\(p^{2} q\) коли\(p=-\frac{1}{2}\) і\(q=\frac{5}{9}\)
- Відповідь
-
\(\frac{5}{9}\)
5\(m^{2} n\) коли\(m=-\frac{2}{5}\) і\(n=\frac{1}{3}\)
\(\frac{u+v}{w}\)коли
\(u=-4, v=-8, w=2\)
- Відповідь
-
-6
\(\frac{m+n}{p}\)коли
\(m=-6, n=-2, p=4\)
Десяткові
Ім'я та запис десяткових знаків
У наступних вправах пишіть як десяткове число.
Вісім і три соті
- Відповідь
-
8.03
Дев'ять і сім сотих
Тисячна
- Відповідь
-
0,001
Дев'ять тисячних
У наступних вправах назвіть кожну десяткову.
7.8
- Відповідь
-
сім і вісім десятих
5.01
0,005
- Відповідь
-
п'ять тисячних
0,381
Круглі десяткові
У наступних вправах округляйте кожне число до найближчого
- сотий
- десятий
- ціле число.
5.7932
- Відповідь
-
- 5.79
- 5.8
- 6
3 6284
12.4768
- Відповідь
-
- 12.48
- 12.5
- 12
25.8449
Додавання та віднімання десяткових знаків
У наступних вправах додайте або відніміть.
18,37+9,36
- Відповідь
-
27.73
256.37−85.49
15.35−20.88
- Відповідь
-
−5.53
37,5+12,23
−4.2+ (−9.3)
- Відповідь
-
−13,5
−8.6+ (−8.6)
100−64.2
- Відповідь
-
35.8
100−65.83
2,51+40
- Відповідь
-
42.51
9,38+60
Множення та ділення десяткових знаків
У наступних вправах помножте.
(0.3) (0.4)
- Відповідь
-
0,12
(0.6) (0.7)
(8.52) (3.14)
- Відповідь
-
26.7528
(5.32) (4.86)
(0.09) (24.78)
- Відповідь
-
2.2302
(0.04) (36.89)
У наступних вправах розділіть.
\(0.15 \div 5\)
- Відповідь
-
0,03
\(0.27 \div 3\)
\(\$ 8.49 \div 12\)
- Відповідь
-
$0.71
\(\$ 16.99 \div 9\)
\(12 \div 0.08\)
- Відповідь
-
150
\(5 \div 0.04\)
Перетворення десяткових дробів, дробів та відсотків
У наступних вправах запишіть кожну десяткову дробу як дріб.
0,08
- Відповідь
-
\(\frac{2}{25}\)
0,17
0,425
- Відповідь
-
\(\frac{17}{40}\)
0.184
1.75
- Відповідь
-
\(\frac{7}{4}\)
0,035
У наступних вправах перетворіть кожен дріб в десятковий.
\(\frac{2}{5}\)
- Відповідь
-
0.4
\(\frac{4}{5}\)
\(-\frac{3}{8}\)
- Відповідь
-
−0,375
\(-\frac{5}{8}\)
\(\frac{5}{9}\)
- Відповідь
-
\(0 . \overline{5}\)
\(\frac{2}{9}\)
\(\frac{1}{2}+6.5\)
- Відповідь
-
7
\(\frac{1}{4}+10.75\)
У наступних вправах перетворіть кожен відсоток в десятковий.
5%
- Відповідь
-
0,05
9%
40%
- Відповідь
-
0.4
50%
115%
- Відповідь
-
1.15
125%
У наступних вправах перетворіть кожне десяткове число в відсоток.
0,18
- Відповідь
-
18%
0,15
0,009
- Відповідь
-
0,9%
0,008
1.5
- Відповідь
-
150%
2.2
Реальні числа
Спрощення виразів за допомогою квадратних коренів
У наступних вправах спростити.
\(\sqrt{64}\)
- Відповідь
-
8
\(\sqrt{144}\)
\(-\sqrt{25}\)
- Відповідь
-
-5
\(-\sqrt{81}\)
Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел
У наступних вправах запишіть як співвідношення двох цілих чисел.
- 9
- 8.47
- Відповідь
-
- \(\frac{9}{1}\)
- \(\frac{847}{100}\)
- −15
- 3.591
У наступних вправах перерахуйте
- раціональні числа,
- ірраціональні числа.
\(0.84,0.79132 \ldots, 1 . \overline{3}\)
- Відповідь
-
- \(0.84,1.3\)
- \(0.79132 \ldots\)
\(2.3 \overline{8}, 0.572,4.93814 \ldots\)
У наступних вправах визначте, чи є кожне число раціональним чи ірраціональним.
- \(\sqrt{121}\)
- \(\sqrt{48}\)
- Відповідь
-
- раціональні
- ірраціональний
- \(\sqrt{56}\)
- \(\sqrt{16}\)
У наступних вправах визначте, чи є кожне число дійсним числом чи ні дійсним числом.
- \(\sqrt{-9}\)
- \(-\sqrt{169}\)
- Відповідь
-
- не дійсне число
- дійсне число
- \(\sqrt{-64}\)
- \(-\sqrt{81}\)
У наступних вправах перерахуйте
- цілих чисел,
- цілих чисел,
- раціональні числа,
- ірраціональні числа,
- дійсні числа для кожного набору чисел.
\(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
- Відповідь
-
- \(0, \sqrt{16}\)
- \(-4,0, \sqrt{16}\)
- \(-4,0, \frac{5}{6}, \sqrt{16}\)
- \(\sqrt{18}, 5.2537 \ldots\)
- \(-4,0, \frac{5}{6}, \sqrt{16}, \sqrt{18}, 5.2537 \ldots\)
\(-\sqrt{4}, 0 . \overline{36}, \frac{13}{3}, 6.9152 \ldots, \sqrt{48}, 10 \frac{1}{2}\)
Знайдіть дроби на числовому рядку
У наступних вправах знайдіть цифри на числовому рядку.
\(\frac{2}{3}, \frac{5}{4}, \frac{12}{5}\)
- Відповідь
-
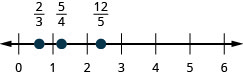
\(\frac{1}{3}, \frac{7}{4}, \frac{13}{5}\)
\(2 \frac{1}{3},-2 \frac{1}{3}\)
- Відповідь
-
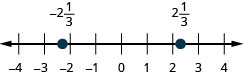
\(1 \frac{3}{5},-1 \frac{3}{5}\)
У наступних вправах замовте кожну з наступних пар чисел, використовуючи < or >.
−1___\(-\frac{1}{8}\)
- Відповідь
-
<
\(-3 \frac{1}{4}\)___−4
\(-\frac{7}{9}\)___\(\frac{4}{9}\)
- Відповідь
-
>
\(-2\)___\(\frac{19}{8}\)
Знайдіть десяткові числа на цифровому рядку
У наступних вправах знайдіть на числовому рядку.
0.3
- Відповідь
-
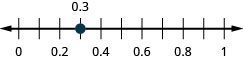
−0,2
−2.5
- Відповідь
-
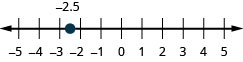
2.7
У наступних вправах замовте кожну з наступних пар чисел, використовуючи < or >.
0.9___0.6
- Відповідь
-
>
0.7___0.8
−0.6___−0,59
- Відповідь
-
>
−0.27___−0,3
Властивості дійсних чисел
Використання комутативних та асоціативних властивостей
У наступних вправах використовуйте асоціативну властивість для спрощення.
−12 (4м)
- Відповідь
-
−48 м
30\(\left(\frac{5}{6} q\right)\)
(а+16) +31
- Відповідь
-
а+47
(с+0,2) +0,7
У наступних вправах спростити.
6 р+37+ (−6 років)
- Відповідь
-
37
\(\frac{1}{4}+\frac{11}{15}+\left(-\frac{1}{4}\right)\)
\(\frac{14}{11} \cdot \frac{35}{9} \cdot \frac{14}{11}\)
- Відповідь
-
\(\frac{35}{9}\)
\(-18 \cdot 15 \cdot \frac{2}{9}\)
\(\left(\frac{7}{12}+\frac{4}{5}\right)+\frac{1}{5}\)
- Відповідь
-
1\(\frac{7}{12}\)
(3,98д+0,75 д) +1,25д
11х+8х+16х+15 років
- Відповідь
-
27 х+23 роки
52м+ (−20н) + (−18м) + (−5н)
Використання ідентичності та обернених властивостей додавання та множення
У наступних вправах знайдіть добавку, зворотну кожному числу.
- \(\frac{1}{3}\)
- 5.1
- \(-14\)
- \(-\frac{8}{5}\)
- Відповідь
-
- \(-\frac{1}{3}\)
- \(-5.1\)
- -14
- \(-\frac{8}{5}\)
- \(-\frac{7}{8}\)
- \(-0.03\)
- 17
- \(\frac{12}{5}\)
У наступних вправах знайдіть мультиплікативний зворотний кожного числа.
- \(10\)
- \(-\frac{4}{9}\)
- 0.6
- Відповідь
-
- \(\frac{1}{10}\)
- \(-\frac{9}{4}\)
- \(\frac{5}{3}\)
- \(-\frac{9}{2}\)
- -7
- 2.1
Використання властивостей нуля
У наступних вправах спростити.
83\(\cdot 0\)
- Відповідь
-
0
\(\frac{0}{9}\)
\(\frac{5}{0}\)
- Відповідь
-
невизначений
\(0 \div \frac{2}{3}\)
У наступних вправах спростити.
43+39+ (−43)
- Відповідь
-
39
(н+6,75) +0.25
\(\frac{5}{13} \cdot 57 \cdot \frac{13}{5}\)
- Відповідь
-
57
\(\frac{1}{6} \cdot 17 \cdot 12\)
\(\frac{2}{3} \cdot 28 \cdot \frac{3}{7}\)
- Відповідь
-
8
\(9(6 x-11)+15\)
Спрощення виразів за допомогою властивості розподілу
У наступних вправах спростіть використання розподільної властивості.
7 (х+9)
- Відповідь
-
7х+63
9 (u−4)
−3 (6м−1)
- Відповідь
-
−18 м+3
−8 (−7а−12)
\(\frac{1}{3}(15 n-6)\)
- Відповідь
-
5н−2
\((y+10) \cdot p\)
(a−4) − (6а+9)
- Відповідь
-
−5а−13
4 (х+3) −8 (х−7)
Системи вимірювань
1.1 Визначте одиниці виміру США та перетворіть з однієї одиниці в іншу
У наступних вправах перетворіть одиниці. Округлити до найближчої десятої.
Квіткова альтанка висотою 7 футів. Перетворіть висоту в дюйми.
- Відповідь
-
84 дюймів
Картинна рамка шириною 42 дюйми. Перетворіть ширину в фути.
Келлі має висоту 5 футів 4 дюйми. Перетворіть її висоту в дюйми.
- Відповідь
-
64 дюймів
Дитячий майданчик шириною 45 футів. Перетворіть ширину в ярди.
Висота гори Шаста становить 14 179 футів. Перетворіть висоту в милі.
- Відповідь
-
2,7 милі
Шаму важить 4,5 тонни. Перетворіть вагу в фунти.
Вистава тривала\(1\frac{3}{4}\) годинами. Перетворіть час в хвилини.
- Відповідь
-
105 хвилин
Скільки столових ложок в кварті?
Дитина Наомі важила 5 фунтів 14 унцій при народженні. Перетворіть вагу в унції.
- Відповідь
-
94 унції
Trinh потребує 30 чашок фарби для її класного художнього проекту. Перетворіть обсяг в галони.
Використовуйте змішані одиниці виміру в системі США.
У наступних вправах вирішуйте.
Джон зловив 4 омарів. Ваги омарів становили 1 фунт 9 унцій, 1 фунт 12 унцій, 4 фунтів 2 унції та 2 фунтів 15 унцій. Якою була загальна вага омарів?
- Відповідь
-
10 фунтів. 6 унцій
Кожен день минулого тижня Педро записував кількість хвилин, які він витратив на читання. Кількість хвилин становило 50, 25, 83, 45, 32, 60, 135. Скільки годин Педро витратив на читання?
Фуад має висоту 6 футів 2 дюйми. Якщо він стоїть на сходинці сходів 8 футів 10 дюймів у висоту, наскільки високо від землі знаходиться вершина голови Фуада?
- Відповідь
-
15 футів
Даліла хоче зробити кинути чохли для подушок. Кожна обкладинка займає 30 дюймів тканини. Скільки ярдів тканини їй потрібно для 4 чохлів?
Здійснення конверсій одиниць у метричній системі
У наступних вправах перетворіть одиниці.
Донна - 1,7 метра заввишки. Перетворіть її зростання в сантиметри.
- Відповідь
-
170 сантиметрів
Гора Еверест має висоту 8 850 метрів. Перетворіть висоту в кілометри.
Одна чашка йогурту містить 488 міліграм кальцію. Перетворіть це в грами.
- Відповідь
-
0,488 грам
Одна чашка йогурту містить 13 грам білка. Перетворіть це в міліграми.
Серхіо важив 2,9 кілограма при народженні. Перетворіть це в грами.
- Відповідь
-
2 900 грам
Пляшка води містила 650 мілілітрів. Перетворіть це в літри.
Використання змішаних одиниць виміру в метричній системі
У наступних вправах вирішуйте.
Мін - 2 метри заввишки. Його дочка зростом 88 сантиметрів. Наскільки вище Мін, ніж його дочка?
- Відповідь
-
1,12 метра
У Сельми була 1 літрова пляшка води. Якщо вона випила 145 мілілітрів, скільки води залишилося в пляшці?
Одна порція журавлинного соку містить 30 грам цукру. Скільки кілограмів цукру в 30 порціях журавлинного соку?
- Відповідь
-
0.9 кілограмів
Одна унція тофу забезпечила 2 грами білка. Скільки міліграмів білка забезпечують 5 унцій тофу?
Перетворення між США та метричними системами вимірювання
У наступних вправах зробіть перетворення одиниць. Округлити до найближчої десятої.
Маджид має висоту 69 дюймів. Перетворіть його зростання в сантиметри.
- Відповідь
-
175.3 сантиметри
Баскетбольний майданчик коледжу 84 футів в довжину. Перетворіть цю довжину в метри.
Керолайн пройшла 2,5 кілометра. Перетворіть цю довжину в милі.
- Відповідь
-
2,6 км
Лукас важить 78 кілограмів. Перетворіть його вагу в фунти.
Автомобіль Стіва вміщує 55 літрів газу. Перетворіть це на галони.
- Відповідь
-
14,6 галонів
Коробка з книгами важить 25 фунтів. Перетворіть вагу в кілограми.
Перетворення між температурами Фаренгейта та Цельсія
У наступних вправах перетворіть температуру Фаренгейта в градуси Цельсія. Округлити до найближчої десятої.
95° за Фаренгейтом
- Відповідь
-
35° C
23° Фаренгейт
20° за Фаренгейтом
- Відповідь
-
—6.7° C
64° Фаренгейт
У наступних вправах перетворіть температуру Цельсія в градуси за Фаренгейтом. Округлити до найближчої десятої.
30° за Цельсієм
- Відповідь
-
86° Ф
-5° за Цельсієм
-12° за Цельсієм
- Відповідь
-
10.4° Ф
24° за Цельсієм
Розділ Практика Тест
Напишіть цілим числом, використовуючи цифри: двісті п'ять тисяч, шістсот сімнадцять.
- Відповідь
-
205 617
Знайдіть просте факторизацію 504.
Знайдіть найменш поширене кратне 18 і 24.
- Відповідь
-
72
Поєднувати подібні терміни: 5n+8+2n−1.
У наступних вправах оцініть.
\(-|x|\)коли\(x=-2\)
- Відповідь
-
−2
11−a, коли a=−3
Переведіть на алгебраїчний вираз і спростіть: на двадцять менше негативного 7.
- Відповідь
-
−7−20; −27
Баланс Моніка становить −18 доларів на її розрахунковому рахунку. Вона вносить на рахунок 152 долари. Що таке новий баланс?
Округлення 677.1348 до найближчої сотої.
- Відповідь
-
677.13
Перетворити\(\frac{4}{5}\) на десяткове число.
Перетворіть 1,85 до відсотка.
- Відповідь
-
185%
Знайдіть\(\frac{2}{3},-1.5,\) і\(\frac{9}{4}\) на числовому рядку.
У наступних вправах спрощуйте кожен вираз.
\(4+10(3+9)-5^{2}\)
- Відповідь
-
99
−85+42
−19−25
- Відповідь
-
−44
\((-2)^{4}\)
\(-5(-9) \div 15\)
- Відповідь
-
3
\(\frac{3}{8} \cdot \frac{11}{12}\)
\(\frac{4}{5} \div \frac{9}{20}\)
- Відповідь
-
\(\frac{16}{9}\)
\(\frac{12+3 \cdot 5}{15-6}\)
\(\frac{m}{7}+\frac{10}{7}\)
- Відповідь
-
\(\frac{m+10}{7}\)
\(\frac{7}{12}-\frac{3}{8}\)
\(-5.8+(-4.7)\)
- Відповідь
-
−10.5
100−64.25
(0.07) (31.95)
- Відповідь
-
2.2365
\(9 \div 0.05\)
\(-14\left(\frac{5}{7} p\right)\)
- Відповідь
-
−10р
(u+8) −9
6х+ (−4г) +9х+8г
- Відповідь
-
15х+4г
\(\frac{0}{23}\)
\(\frac{75}{0}\)
- Відповідь
-
невизначений
−2 (13к−5)
Фільм тривав 1\(\frac{2}{3}\) годину. Скільки хвилин це тривало? (1 година\(=60\) хвилин)
- Відповідь
-
100 хвилин
Позашляховик Майка має висоту 5 футів 11 дюймів. Він хоче покласти вантажний мішок на даху на позашляховик. Вантажний мішок має висоту 1 фут 6 дюймів. Якою буде загальна висота позашляховика з багажною сумкою на даху? (1 фут = 12 дюймів)
Дженніфер пробігла 2,8 милі. Перетворіть цю довжину в кілометри. (1 миля = 1.61 кілометра)
- Відповідь
-
4.508 км
