1.10: Властивості дійсних чисел
- Page ID
- 59072
До кінця цього розділу ви зможете:
- Використовуйте комутативні та асоціативні властивості
- Використовуйте ідентичність та обернені властивості додавання та множення
- Використовувати властивості нуля
- Спрощення виразів за допомогою властивості distributive
Більш ретельне ознайомлення з темами, розглянутими в цьому розділі, можна знайти в розділі Преалгебра, Властивості дійсних чисел.
Використання комутативних та асоціативних властивостей
Подумайте про додавання двох чисел, скажімо 5 і 3. Порядок, який ми їх додаємо, не впливає на результат, чи не так?
\[\begin{array} { cc } { 5 + 3 } & { 3 + 5 } \\ { 8 } & { 8 } \\ { 5 + 3 = } & { 3 + 5 } \end{array}\]
Результати однакові.
Як бачимо, порядок, в якому ми додаємо, значення не має!
А як щодо множення 5 і 3?
\[\begin{array} { c c } { 5 \cdot 3 } & { 3 \cdot 5 } \\ { 15 } & { 15 } \\ { 5 \cdot 3=} &{3 \cdot 5 } \end{array}\]
Знову ж таки, результати ті ж!
Порядок, в якому ми розмножуємо, значення не має!
Ці приклади ілюструють комутативну властивість. При додаванні або множенні зміна порядку дає той же результат.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b \text { are real numbers, then } \quad a + b = b + a } \\ { \textbf { of Multiplication } } & { \text { If } a , b \text { are real numbers, then } \quad a \cdot b = b \cdot a } \end{array}\]
При додаванні або множенні зміна порядку дає той же результат.
Комутативна власність має відношення до порядку. При зміні порядку чисел при додаванні або множенні результат однаковий.
А як щодо віднімання? Чи має значення порядок, коли ми віднімаємо числа? Чи дає 7−3 той самий результат, що і 3−7?
\[\begin{array} { c c } { 7 - 3 } & { 3 - 7 } \\ { 4 } & { - 4 } \end{array}\]
\[\begin{aligned} 4 & \neq - 4 \\ 7 - 3 & \neq 3 - 7 \end{aligned}\]
Результати не однакові.
Оскільки зміна порядку віднімання не дало однакового результату, ми знаємо, що віднімання не є комутативним.
Давайте подивимося, що відбувається, коли ми ділимо два числа. Чи є розподіл комутативним?
\[\begin{array} { cc} { 12 \div 4 } & { 4 \div 12 } \\ { \frac { 12 } { 4 } } & { \frac { 4 } { 12 } } \\ { 3 } & { \frac { 1 } { 3 } } \end{array}\]
\[\begin{aligned} 3 \neq & \frac { 1 } { 3 } \\ 12 \div 4 & \neq 4 \div 12 \end{aligned}\]
Результати не однакові.
Оскільки зміна порядку поділу не дало однакового результату, поділ не є комутативним. Комутативні властивості застосовуються лише до додавання та множення!
- Додавання і множення є комутативними.
- Віднімання та поділ не є комутативними.
Якби вас попросили спростити цей вираз, як би ви це зробили і якою була б ваша відповідь?
\[7 + 8 + 2\]
Деякі люди думають, що\(7+8\) це 15, а потім\(15+2\) 17. Інші можуть починатися з\(8+2\) робить 10, а потім\(7+10\) робить 17.
Будь-який спосіб дає однаковий результат. Пам'ятайте, що ми використовуємо дужки як символи групування, щоб вказати, яку операцію слід виконати в першу чергу.
\[\begin{array} { ll } { \text{ Add } 7 + 8 . } & { ( 7 + 8 ) + 2 } \\ { \text { Add. } } & { 15 + 2 } \\ { \text { Add. } } & { 17 } \\ \\ { } & { 7 + ( 8 + 2 ) } \\ { \text { Add } 8 + 2 . } & { 7 + 10 } \\ { \text { Add. } } & { 77 } \\\\ { ( 7 + 8 ) + 2 = 7 + ( 8 + 2 ) } \end{array}\]
При складанні трьох чисел зміна угруповання чисел дає однаковий результат.
Це справедливо і для множення.
\[\begin{array} { ll } { } & { (5\cdot \frac{1}{3})\cdot 3 } \\ { \text { Multiply. } 5\cdot \frac{1}{3} } & { \frac{5}{3}\cdot 3 } \\ { \text { Multiply. } } & { 5 } \\ \\ { } & { 5\cdot (\frac{1}{3}\cdot 3) } \\ { \text { Multiply. } \frac{1}{3}\cdot 3 } & { 5\cdot 1 } \\ { \text { Multiply. } } & { 5 } \\ \\ { (5\cdot \frac{1}{3})\cdot 3 = 5\cdot (\frac{1}{3}\cdot 3) } \end{array}\]
При множенні трьох чисел зміна угруповання чисел дає однаковий результат.
Ви, напевно, знаєте це, але термінологія може бути для вас новою. Ці приклади ілюструють асоціативну властивість.
\[\begin{array} { l l } { \textbf { of Addition } } & { \text { If } a , b , c \text { are real numbers, then } ( a + b ) + c = a + ( b + c ) } \\ { \textbf { of Multiplication } } & { \text { If } a , b , c \text { are real numbers, then } ( a \cdot b ) \cdot c = a \cdot ( b \cdot c ) } \end{array}\]
При додаванні або множенні зміна угруповання дає той же результат.
Давайте ще раз подумаємо про множення\(5\cdot \frac{1}{3}\cdot 3\). Ми отримали однаковий результат обома способами, але який шлях був простіше? Множення\(\frac{1}{3}\) і 3 спочатку, як показано вище з правого боку, виключає дріб на першому кроці. Використання асоціативної властивості може полегшити математику!
Асоціативне властивість має відношення до групування. Якщо ми змінимо спосіб групування чисел, результат буде однаковим. Зверніть увагу, що це ті ж три числа в тому ж порядку - єдина різниця полягає в групуванні.
Ми побачили, що віднімання та поділ не були комутативними. Вони також не асоціативні.
Спрощуючи вираз, завжди є гарною ідеєю планувати, якими будуть кроки. Для того, щоб об'єднати подібні терміни в наступному прикладі, ми будемо використовувати комутативну властивість додавання, щоб написати подібні терміни разом.
Спростити:\(18p+6q+15p+5q\).
- Відповідь
-
\[\begin{array} { l l} {} &{18p+6q+15p+5q}\\ \\{ \text { Use the commutative property of addition } } &{} \\ { \text {to re-order so that like terms are together.} } &{18p+15p+ 6q+5q} \\ \\ {\text{Add like terms.}} &{33p + 11q} \end{array}\]
Спростити:\(23r+14s+9r+15s\).
- Відповідь
-
\(32r+29s\)
Спростити:\(37m+21n+4m−15n\).
- Відповідь
-
\(41m+6n\)
Коли нам доводиться спростити алгебраїчний вираз s, ми часто можемо полегшити роботу, застосувавши комутативну або асоціативну властивість спочатку, замість того, щоб автоматично дотримуватися порядку операцій. При додаванні або відніманні дробів спочатку об'єднайте ті, що мають спільний знаменник.
Спростити:\((\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}\)
- Відповідь
-
\[\begin{array} { l l } {} &{(\frac{5}{13} + \frac{3}{4}) + \frac{1}{4}} \\{ \text { Notice that the last } 2 \text { terms have a } } \\ { \text { common denominator, so change the } } &{\frac { 5 } { 13 } + \left( \frac { 3 } { 4 } + \frac { 1 } { 4 } \right)}\\ { \text { grouping. } } &{}\\ \\ {\text{Add in parentheses first.}} &{\frac{5}{13} + (\frac{4}{4})} \\ \\ {\text{Simplify the fraction.}} &{\frac{5}{13} + 1} \\ \\ {\text{Add.}} &{1\frac{5}{13}} \\ \\ {\text{Convert to an improper fraction.}} &{\frac{18}{13}} \end{array}\]
Спростити:\((\frac{7}{15} + \frac{5}{8}) + \frac{3}{8}\)
- Відповідь
-
\(1\frac{7}{15}\)
Спростити:\((\frac{2}{9} + \frac{7}{12}) + \frac{5}{12}\)
- Відповідь
-
\(1\frac{2}{9}\)
Використовуйте асоціативну властивість для спрощення\(6(3x)\).
- Відповідь
-
Використовуйте асоціативне властивість множення,\((a\cdot b)\cdot c=a\cdot (b\cdot c)\), для зміни угруповання.
\[\begin{array} { ll } {} &{ 6 ( 3 x ) } \\ { \text { Change the grouping. } } &{(6\cdot 3)x} \\ { \text { Multiply in the parentheses. } } &{18} \end{array}\]
Зверніть увагу, що ми можемо множити,\(6\cdot 3\) але ми не могли помножити, не\(3x\) маючи значення для\(x\).
Використовуйте асоціативну властивість для спрощення\(8(4x)\).
- Відповідь
-
\(32x\)
Використовуйте асоціативну властивість для спрощення\(-9(7y)\).
- Відповідь
-
\(-63y\)
Використання ідентичності та обернених властивостей додавання та множення
Що відбувається, коли ми додаємо 0 до будь-якого числа? Додавання 0 не змінює значення. З цієї причини ми називаємо 0 аддитивної ідентичністю.
Наприклад,
\[\begin{array} { c c c } { 13 + 0 } & { - 14 + 0 } & { 0 + ( - 8 ) } \\ { 13 } & { - 14 } & { - 8 } \end{array}\]
Ці приклади ілюструють властивість Identity of Addition, яка стверджує, що для будь-якого дійсного числа\(a\),\(a+0=a\) і\(0+a=a\).
Що відбувається, коли ми помножимо будь-яке число на одиницю? Множення на 1 не змінює значення. Таким чином, ми називаємо 1 мультиплікативна ідентичність.
Наприклад,\[\begin{array} { r r r } { 43 \cdot 1 } & { - 27 \cdot 1 } & { 1 \cdot \frac { 3 } { 5 } } \\ { 43 } & { - 27 } & { \frac { 3 } { 5 } } \end{array}\]
Ці приклади ілюструють властивість ідентичності множення, яка стверджує, що для будь-якого дійсного числа\(a\),\(a\cdot 1=a\) і\(1\cdot a=a\).
Ми підсумовуємо властивості ідентичності нижче.
\[\begin{array} { l l} { \textbf {of addition}\text{ For any real number } a : } &{ a + 0 = a \quad 0 + a = a } \\ { \textbf{0} \text { is the}\textbf{ additive identity } } \\ {\textbf {of multiplication}\text{ For any real number } a : } &{ a \cdot 1 = a \quad 1 \cdot a = a } \\ { \textbf{1}\text{ is the}\textbf{ multiplicative identity } } \end{array}\]

Зверніть увагу, що в кожному випадку відсутнє число було протилежним числу!
Викликаємо\(−a\). добавку, обернену a. Протилежністю числу є його адитивна зворотна. Число і його протилежність додають до нуля, що є адитивною ідентичністю. Це призводить до зворотного властивості додавання, яке вказує на будь-яке дійсне число\(a, a+(−a)=0\). Пам'ятайте, число і його протилежність додають до нуля.
Яке число, помножене на\(\frac{2}{3}\) дає мультиплікативну ідентичність, 1? Іншими словами,\(\frac{2}{3}\) раз, що призводить до 1?

Яке число, помножене на 2, дає мультиплікативну ідентичність, 1? Іншими словами, в 2 рази, що призводить до 1?

Зверніть увагу, що в кожному випадку відсутнє число було відповідним числу!
Ми\(\frac{1}{a}\) називаємо мультиплікативну обернену a. Зворотне число aa є його мультиплікативним оберненим. Число і його зворотне множення на одиницю, що є мультиплікативною ідентичністю. Це призводить до оберненої властивості множення, яка стверджує, що для будь-якого дійсного числа\(a, a\neq 0, a\cdot \frac{1}{a}=1\).
Ми формально вкажемо зворотні властивості тут:
\[\begin{array} { l l l } { \textbf { of addition } } &{ \text { For any real number } a,} &{a + (-a) = 0}\\{} &{-a \text{. is the}\textbf{ additive inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its opposite add to zero. } }&{}\\ \\{ \textbf { of multiplication } } &{ \text { For any real number } a, a\neq 0} &{a\cdot \frac{1}{a} = 1}\\{} &{\frac{1}{a} \text{. is the}\textbf{ multiplicative inverse} \text{ of }a} &{}\\ {} &{ \text { A number and its reciprocal multiply to zero. } }&{} \end{array}\]
Знайти добавку, обернену
- \(\frac{5}{8}\)
- \(0.6\)
- \(-8\)
- \(-\frac{4}{3}\)
- Відповідь
-
Щоб знайти добавку, обернену, знаходимо протилежне.
- Добавка, зворотна\(\frac{5}{8}\), протилежна\(\frac{5}{8}\). Добавка, обернена\(\frac{5}{8}\) є\(-\frac{5}{8}\)
- Добавка, зворотна\(0.6\), протилежна\(0.6\). Добавка, обернена\(0.6\) є\(-0.6\).
- Добавка, зворотна\(-8\), протилежна\(-8\). Пишемо протилежне\(-8\) as\(-(-8)\), а потім спрощуємо його до\(8\). Тому добавка обернена\(-8\) є\(8\).
- Добавка, зворотна\(-\frac{4}{3}\), протилежна\(-\frac{4}{3}\). Пишемо це як\(-(-\frac{4}{3})\), а потім спрощуємо до\(\frac{4}{3}\). Таким чином, добавка обернена\(-\frac{4}{3}\) є\(\frac{4}{3}\).
Знайти добавку, обернену
- \(\frac{7}{9}\)
- \(1.2\)
- \(-14\)
- \(-\frac{9}{4}\)
- Відповідь
-
- \(-\frac{7}{9}\)
- \(-1.2\)
- \(14\)
- \(\frac{9}{4}\)
Знайти добавку, обернену
- \(\frac{7}{13}\)
- \(8.4\)
- \(-46\)
- \(-\frac{5}{2}\)
- Відповідь
-
- \(-\frac{7}{13}\)
- \(-8.4\)
- \(46\)
- \(\frac{5}{2}\)
Знайти мультиплікативну обернену
- \(9\)
- \(-\frac{1}{9}\)
- \(0.9\)
- Відповідь
-
Щоб знайти мультиплікативний зворотний, знаходимо зворотне.
- Мультиплікативний обернений\(9\) є зворотним з\(9\), який є\(\frac{1}{9}\). Тому мультиплікативний зворотний\(9\) є\(\frac{1}{9}\).
- Мультиплікативний обернений\(-\frac{1}{9}\) є зворотним з\(-\frac{1}{9}\), який є\(−9\). Таким чином, мультиплікативний зворотний\(-\frac{1}{9}\) є\(-9\).
- Щоб знайти мультиплікативний обернений\(0.9\), ми спочатку перетворимо\(0.9\) на дріб,\(\frac{9}{10}\). Потім знаходимо зворотну дробу. Відповідне\(\frac{9}{10}\) є\(\frac{10}{9}\). Таким чином, мультиплікативний зворотний\(0.9\) є\(\frac{10}{9}\).
Знайти мультиплікативну обернену
- \(4\)
- \(-\frac{1}{7}\)
- \(0.3\)
- Відповідь
-
- \(\frac{1}{4}\)
- \(-7\)
- \(\frac{10}{3}\)
Знайти мультиплікативну обернену
- \(18\)
- \(-\frac{4}{5}\)
- \(0.6\)
- Відповідь
-
- \(\frac{1}{18}\)
- \(-\frac{5}{4}\)
- \(\frac{5}{3}\)
Використовувати властивості нуля
Властивість identity додавання говорить, що коли ми додаємо 0 до будь-якого числа, результат - це те саме число. Що відбувається, коли ми помножимо число на 0? Множення на 0 робить добуток рівним нулю.
Для будь-якого дійсного числа a.
\[a \cdot 0 = 0 \quad 0 \cdot a = 0\]
Добуток будь-якого дійсного числа і 0 дорівнює 0.
А як щодо поділу за участю нуля? Що таке\(0\div 3\)? Подумайте про реальний приклад: якщо в банку печива немає печива і 3 людини повинні поділитися ними, скільки печива отримує кожна людина? Немає файлів cookie для спільного використання, тому кожна людина отримує 0 файлів cookie. Отже,
\[0\div 3 = 0\]
Ми можемо перевірити ділення з відповідним фактом множення.
\[12 \div 6 = 2 \text { because } 2 \cdot 6 = 12\]
Отже, ми знаємо,\(0\div 3=0\) тому що\(0\cdot 3=0\).
Для будь-якого дійсного числа a, крім\(0, \frac{0}{a}=0\) і\(0\div a=0\).
Нуль ділиться на будь-яке дійсне число, крім нуля, дорівнює нулю.
Тепер подумайте про поділ на нуль. Який результат ділення 4 на 0? Подумайте про пов'язаний факт множення:\(4\div 0=?\) значить\(?\cdot 0=4\). Чи є число, яке помножене на 0 дає 4? Оскільки будь-яке дійсне число, помножене на 0, дає 0, не існує реального числа, яке можна помножити на 0, щоб отримати 4.
Ми робимо висновок, що відповіді немає,\(4\div 0\) і тому ми говоримо, що поділ на 0 не визначено.
Для будь-якого дійсного числа a, крім\(0, \frac{a}{0}\) і\(a\div 0\) не визначені.
Ділення на нуль не визначено.
Підсумовуємо властивості нуля нижче.
Множення на нуль: для будь-якого дійсного числа
\[a \cdot 0 = 0 \quad 0 \cdot a = 0 \quad \text { The product of any number and } 0 \text { is } 0\]
Ділення нуля, поділ на нуль: Для будь-якого дійсного числа\(a, a\neq 0\)
\[\begin{array} { l l } { \frac { 0 } { a } = 0 } & { \text { Zero divided by any real number, except itself is zero. } } \\ { \frac { a } { 0 } \text { is undefined } } & { \text { Division by zero is undefined. } } \end{array}\]
Спростити:
- \(-8\cdot 0\)
- \(\frac{0}{-2}\)
- \(\frac{-32}{0}\)
- Відповідь
-
- \[\begin{array} { cc } { } &{-8\cdot 0}\\{\text{The product of any real number and 0 is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{0}{-2}}\\{\text{Zero divided by any real number, except}} &{} \\ {\text{itself, is 0}} &{0}\end{array}\]
- \[\begin{array} { ll } { } &{\frac{-32}{0}}\\ {\text{Division by 0 is undefined.}} &{\text{undefined}} \end{array}\]
Спростити:
- \(-14\cdot 0\)
- \(\frac{0}{-6}\)
- \(\frac{-2}{0}\)
- Відповідь
-
- \(0\)
- \(0\)
- невизначений
Спростити:
- \(0(-17)\)
- \(\frac{0}{-10}\)
- \(\frac{-5}{0}\)
- Відповідь
-
- \(0\)
- \(0\)
- невизначений
Тепер ми будемо практикувати використання властивостей тотожностей, зворотних і нульових для спрощення виразів.
Спростити:
- \(\frac{0}{n + 5}\), де\(n\neq −5\)
- \(\frac{10 - 3p}{0}\)де\(10 - 3p \neq 0\)
- Відповідь
-
- \[\begin{array} { ll } { } &{\frac{0}{n + 5}}\\ {\text { Zero divided by any real number except }} &{0} \\ { \text { itself is } 0.} &{} \end{array}\]
- \[\begin{array} { ll } { } &{\frac{10 - 3p}{0}}\\ {\text { Division by 0 is undefined }} &{\text{undefined}} \end{array}\]
Спростити:\(−84n+(−73n)+84n\).
- Відповідь
-
\[\begin{array} { l l } { } &{−84n+(−73n)+84n} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { opposites; use the commutative property of } } &{- 84 n + 84 n + ( - 73 n ) } \\ { \text { addition to re-order the terms. } } &{} \\ \\ { \text { Add left to right. } } &{0 + (-73)}\\ \\{ \text { Add. } } &{-73n} \end{array}\]
Спростити:\(−27a+(−48a)+27a\).
- Відповідь
-
\(−48a\)
Спростити:\(39x+(−92x)+(−39x)\).
- Відповідь
-
\(−92x\)
Тепер ми побачимо, як корисно розпізнавати взаємні дії. Перш ніж множити зліва направо, шукайте взаємні - їх продукт дорівнює 1.
Спростити:\(\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}\)
- Відповідь
-
\[\begin{array} { l l } { } &{\frac{7}{15}\cdot\frac{8}{23}\cdot\frac{15}{7}} \\ { \text { Notice that the first and third terms are } } &{}\\ { \text { reciprocals, so use the commutative } } &{\frac{7}{15}\cdot\frac{15}{7}\cdot\frac{8}{23}} \\ { \text { property of multiplication to re-order the } } &{} \\ { \text { factors. } } &{}\\ \\{ \text { Multiply left to right. } } &{1\cdot\frac{8}{23}} \\\\{\text{Multiply.}} &{\frac{8}{23}}\end{array}\]
Спростити:\(\frac{9}{16}\cdot\frac{5}{49}\cdot\frac{16}{9}\)
- Відповідь
-
\(\frac{5}{49}\)
Спростити:\(\frac{6}{17}\cdot\frac{11}{25}\cdot\frac{17}{6}\)
- Відповідь
-
\(\frac{11}{25}\)
Спростити:
- \(\frac{0}{m + 7}\), де\(m \neq -7\)
- \(\frac{18 - 6c}{0}\), де\(18 - 6c \neq 0\)
- Відповідь
-
- 0
- невизначений
Спростити:
- \(\frac{0}{d - 4}\), де\(d \neq 4\)
- \(\frac{15 - 4q}{0}\), де\(15 - 4q \neq 0\)
- Відповідь
-
- 0
- невизначений
Спростити:\(\frac{3}{4}\cdot\frac{4}{3}(6x + 12)\)
- Відповідь
-
\[\begin{array} { l l } { } &{\frac{3}{4}\cdot\frac{4}{3}(6x + 12)} \\ { \text { There is nothing to do in the parentheses, } } &{}\\ { \text { so multiply the two fractions first—notice, } } &{1(6x + 12)} \\ { \text { they are reciprocals. } } &{} \\ \\{ \text { Simplify by recognizing the multiplicative } } &{} \\{\text{ identity.}} &{6x + 12} \end{array}\]
Спростити:\(\frac{2}{5}\cdot\frac{5}{2}(20y + 50)\)
- Відповідь
-
\(20y + 50\)
Спростити:\(\frac{3}{8}\cdot\frac{8}{3}(12z + 16)\)
- Відповідь
-
\(12z + 16\)
Спрощення виразів за допомогою властивості розподілу
Припустимо, що в кіно збираються троє друзів. Кожному з них потрібно $9.25 - це 9 доларів і 1 квартал - щоб оплатити свої квитки. Скільки грошей їм потрібно всім разом?
Можна подумати про доларах окремо від кварталів. Їм потрібно 3 рази $9 так $27, і 3 рази 1 квартал, так 75 центів. Всього їм потрібно $27,75. Якщо ви думаєте про те, щоб зробити математику таким чином, ви використовуєте розподільну властивість.
\[\begin{array} { rr } {\text { If } a , b , c \text { are real numbers, then }} &{a ( b + c ) = a b + a c} \\ \\{ \text { Also,} } &{( b + c ) a = b a + c a} \\ {} &{a ( b - c ) = a b - a c } &{} \\{} &{( b - c ) a = b a - c a } \end{array}\]
Повернувшись до наших друзів у фільмах, ми могли знайти загальну суму грошей, яка їм потрібна, як це:
\[\begin{array} { c } { 3 ( 9.25 ) } \\ { 3 ( 9 + 0.25 ) } \\ { 3 ( 9 ) + 3 ( 0.25 ) } \\ { 27 + 0.75 } \\ \\ { 27.75 } \end{array}\]
В алгебрі ми використовуємо властивість distributive для видалення дужок, оскільки ми спрощуємо вирази.
Наприклад, якщо нас попросять спростити вираз\(3(x+4)\), порядок операцій говорить працювати в дужках першим. Але ми не можемо додати х і 4, оскільки вони не схожі на терміни. Таким чином, ми використовуємо розподільну властивість, як показано у Вправі\(\PageIndex{31}\).
Спростити:\(3(x+4)\).
- Відповідь
-
\[\begin{array} { l l } { } & { 3 ( x + 4 ) } \\ { \text { Distribute. } } & { 3 \cdot x + 3 \cdot 4 } \\ { \text { Multiply. } } & { 3 x + 12 } \end{array}\]
Спростити:\(4(x+2)\).
- Відповідь
-
\(4x + 8\)
Спростити:\(6(x+7)\).
- Відповідь
-
\(6x + 42\)
Деякі студенти вважають корисним малювати стрілками, щоб нагадати їм, як використовувати розподільну властивість. Тоді перший крок у Вправи\(\PageIndex{31}\) буде виглядати наступним чином:
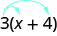
Спростити:\(8(\frac{3}{8}x+\frac{1}{4})\).
- Відповідь
-
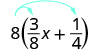
Розподілити. 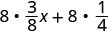
Помножити. 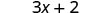
Спростити:\(6(\frac{5}{6}y+\frac{1}{2})\).
- Відповідь
-
\(5y + 3\)
Спростити:\(12(\frac{1}{3}n+\frac{3}{4})\).
- Відповідь
-
\(4n + 9\)
Використання розподільної властивості, як показано у Вправи,\(\PageIndex{37}\) буде дуже корисним, коли ми вирішуємо грошові заявки в наступних розділах.
Спростити:\(100(0.3+0.25q)\).
- Відповідь
-
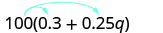
Розподілити. 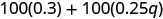
Помножити. 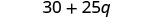
Спростити:\(100(0.7+0.15p)\).
- Відповідь
-
\(70 + 15p\)
Спростити:\(100(0.04+0.35d)\).
- Відповідь
-
\(4 + 35d\)
Коли ми розподіляємо негативне число, нам потрібно бути особливо обережними, щоб знаки були правильними!
Спростити:\(−2(4y+1)\).
- Відповідь
-
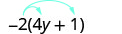
Розподілити. 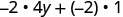
Помножити. 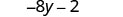
Спростити:\(−3(6m+5)\).
- Відповідь
-
\(−18m-15)\)
Спростити:\(−6(8n+11)\).
- Відповідь
-
\(−48n- 66)\)
Спростити:\(−11(4-3a)\).
- Відповідь
-
Розподілити. 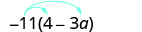
Помножити. 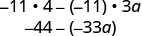
Спростити. 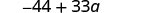
Зверніть увагу, що ви також можете написати результат як\(33a−44\). Знаєте чому?
Спростити:\(−5(2-3a)\).
- Відповідь
-
\(10+ 15a\)
Спростити:\(−7(8-15y)\).
- Відповідь
-
\(-56 + 105y\)
Вправа\(\PageIndex{46}\) покаже, як використовувати розподільну властивість, щоб знайти протилежне виразу.
Спростити:\(−(y+5)\).
- Відповідь
-
\[\begin{array} { ll } {} &{-(y + 5)} \\ \\{ \text {Multiplying by -1 results in the opposite.} } &{-1( y + 5 )} \\ \\ {\text{Distribute.}} &{-1\cdot y + (-1)\cdot 5}\\ \\{\text{Simplify.}} &{-y + (-5)} \\ \\ {} &{-y - 5} \end{array}\]
Спростити:\(−(z-11)\).
- Відповідь
-
\(-z + 11\)
Спростити:\(−(x -4)\).
- Відповідь
-
\(-x + 4\)
Будуть випадки, коли нам потрібно буде використовувати розподільну властивість як частину порядку операцій. Почніть з погляду на дужки. Якщо вираз всередині дужок не можна спростити, наступним кроком буде множення за допомогою властивості distributive, яка видаляє дужки. Наступні два приклади проілюструють це.
Спростити:\(8−2(x + 3)\).
Обов'язково стежте за порядком операцій. Множення відбувається перед відніманням, тому ми спочатку розподілимо 2, а потім віднімаємо.
- Відповідь
-
\[\begin{array} { ll } {} &{8−2(x + 3)} \\ \\{ \text {Distribute.} } &{8−2\cdot x -2\cdot 3} \\ \\ {\text{Multiply.}} &{8 - 2x - 6}\\ \\{\text{Combine like terms.}} &{-2x + 2} \end{array}\]
Спростити:\(9−3(x + 2)\).
- Відповідь
-
\(3 - 3x\)
Спростити:\(7x−5(x + 4)\).
- Відповідь
-
\(2x - 20\)
Спростити:\(4(x - 8)−(x + 3)\).
- Відповідь
-
\[\begin{array} { ll } {} &{4(x - 8)−(x + 3)} \\ \\{ \text {Distribute.} } &{4x - 32 - x - 3} \\ \\{\text{Combine like terms.}} &{3x - 35} \end{array}\]
Спростити:\(6(x - 9)−(x + 12)\).
- Відповідь
-
\(5x - 66\)
Спростити:\(8(x - 1)-(x + 5)\).
- Відповідь
-
\(7x - 13\)
Всі властивості дійсних чисел, які ми використовували в цьому розділі, зведені в табл\(\PageIndex{1}\).
| Комутативне майно | |
| додавання Якщо a, b - дійсні числа, то множення Якщо a, b - дійсні числа, то |
\(a+b=b+a\) \(a\cdot b=b\cdot a\) |
| Асоціативна властивість | |
| додавання Якщо a, b, c - дійсні числа, то множення Якщо a, b, c - дійсні числа, то |
\((a+b)+c=a+(b+c)\) \((a\cdot b)\cdot c=a\cdot (b\cdot c)\) |
| Розподільна власність | |
| Якщо a, b, c є дійсними числами, то | \(a(b+c)=ab+ac\) |
| Ідентичність власності | |
|
додавання Для будь-якого дійсного числа a: множення Для будь-якого дійсного числа a: |
\(a+0=a\) \(0+a=a\) \(1·a=a\) |
| Зворотна властивість | |
| додавання Для будь-якого дійсного числа a \(−a\) є додатковою оберненою a множення Для будь-якого дійсного числа\(a,a\neq 0\) \(\frac{1}{a}\) є мультиплікативний обернений |
\(a+(−a)=0\) \(a\cdot\frac{1}{a}=1\) |
| Властивості нульового | |
|
Для будь-якого дійсного числа a, Для будь-якого реального числа\(a,a\neq 0\) |
\(a\cdot 0=0\) \(0\cdot a=0\) \(\frac{0}{a} = 0\) |
Ключові концепції
- Комутативна власність
- Додавання: Якщо a, b є дійсними числами, то\(a+b=b+a\).
- Множення: Якщо a, b є дійсними числами, то\(a\cdot b=b\cdot a\). При додаванні або множенні зміна порядку дає той же результат.
- Асоціативна властивість
- Додавання: Якщо a, b, c є дійсними числами, то\((a+b)+c=a+(b+c)\).
- Множення: Якщо a, b, c є дійсними числами, то\((a\cdot b)\cdot c=a\cdot (b\cdot c)\).
При додаванні або множенні зміна угруповання дає той же результат.
- розподільна властивість: якщо a, b, c дійсні числа, то
- \(a(b+c)=ab+ac\)
- \((b+c)a=ba+ca\)
- \(a(b-c)=ab-ac\)
- \((b+c)a=ba-ca\)
- Ідентичність власності
- додавання: Для будь-якого дійсного числа a:\(a+0=a\)
0 - це адитивна ідентичність - множення: Для будь-якого дійсного числа a:\(a\cdot 1=a \quad 1·a=a\)
1 1 - мультиплікативна ідентичність
- додавання: Для будь-якого дійсного числа a:\(a+0=a\)
- Зворотна властивість
- додавання: Для будь-якого дійсного числа\(a, a+(−a)=0\). Число і його протилежність додають до нуля. \(−a\)є добавкою, оберненою a.
- множення: Для будь-якого дійсного числа\(a,(a\neq 0)a\cdot\frac{1}{a}=1\). Число і його зворотне множиться на одиницю. \(\frac{1}{a}\)- мультиплікативний обернений a.
- Властивості нульового
- Для будь-якого дійсного числа a,
\(a\cdot 0=0 \quad 0·a=0\) — добуток будь-якого дійсного числа і 0 дорівнює 0. - \(\frac{0}{a}=0\)for\(a\neq 0\) — Нуль ділиться на будь-яке дійсне число, крім нуля дорівнює нулю.
- \(\frac{a}{0}\)не визначено — поділ на нуль не визначено.
- Для будь-якого дійсного числа a,
