1.5: Множення та ділення цілих чисел
- Page ID
- 59028
До кінця цього розділу ви зможете:
- Множення цілих чисел
- Ділити цілі числа
- Спрощення виразів цілими числами
- Оцінити змінні вирази цілими числами
- Перекласти англійські фрази на алгебраїчні вирази
- Використання цілих чисел у додатках
Більш ретельний вступ до тем, розглянутих у цьому розділі, можна знайти в розділі Преалгебра, Цілі числа.
Множення цілих чисел
Оскільки множення є математичним скороченням для повторного додавання, наша модель може бути легко застосована для показу множення цілих чисел. Давайте подивимося на цю конкретну модель, щоб побачити, які візерунки ми помічаємо. Ми будемо використовувати ті ж приклади, які ми використовували для додавання і віднімання. Тут ми будемо використовувати модель лише для того, щоб допомогти нам виявити візерунок.
Ми пам'ятаємо, що\(a\cdot b\) означає додати\(a,\, b\) раз. Тут ми використовуємо модель лише для того, щоб допомогти нам виявити візерунок.
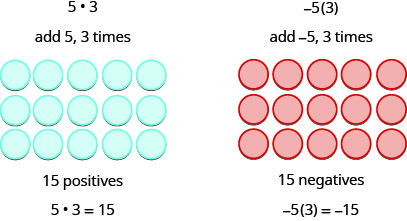
Наступні два приклади більш цікаві.
Що означає множити\(5\) на\(−3\)? Це означає віднімати\(5, 3\) раз. Дивлячись на віднімання як на «віднімання», це означає забрати\(5, 3\) час. Але забирати нічого, тому починаємо з додавання нейтральних пар на робочу область. Потім забираємо\(5\) три рази.
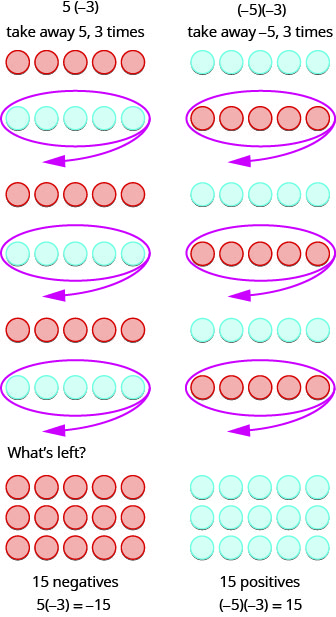
Підсумовуючи:
\[\begin{array} {ll} {5 \cdot 3 = 15} &{-5(3) = -15} \\ {5(-3) = -15} &{(-5)(-3) = 15} \end{array}\]
Зверніть увагу, що для множення двох знакових чисел, коли:
- ознаки однакові, товар позитивний.
- ознаки різні, продукт негативний.
Ми складемо це все разом на графіку нижче.
Для множення двох знакових чисел:
| ті ж ознаки | Продукт | Приклад |
|---|---|---|
| Два позитиву | Позитивні | \(7\cdot 4 = 28\) |
| Два негативу | Позитивні | \(-8(-6) = 48\) |
| Різні прикмети | Продукт | Приклад |
|---|---|---|
| Позитиви\(\cdot\) негативні | Негативний | \(7(-9) = -63\) |
| Негативні\(\cdot\) позитиви | Негативний | \(-5\cdot 10= -50\) |
Помножити:
- \(-9\cdot 3\)
- \(-2(-5)\)
- \(4(-8)\)
- \(7\cdot 6\)
- Відповідь
-
- \[\begin{array} {ll} {} &{-9\cdot 3} \\ {\text{Multiply, noting that the signs are different, so the product is negative.}} &{-27} \end{array}\]
- \[\begin{array} {ll} {} &{-2(-5)} \\ {\text{Multiply, noting that the signs are same, so the product is positive.}} &{10} \end{array}\]
- \[\begin{array} {ll} {} &{4(-8)} \\ {\text{Multiply, with different signs.}} &{-32} \end{array}\]
- \[\begin{array} {ll} {} &{7\cdot 6} \\ {\text{Multiply, with different signs.}} &{42} \end{array}\]
Помножити:
- \(-6\cdot 8\)
- \(-4(-7)\)
- \(9(-7)\)
- \(5\cdot 12\)
- Відповідь
-
- \(-48\)
- \(28\)
- \(-63\)
- \(60\)
Помножити:
- \(-8\cdot 7\)
- \(-6(-9)\)
- \(7(-4)\)
- \(3\cdot 13\)
- Відповідь
-
- \(-56\)
- \(54\)
- \(-28\)
- \(39\)
Коли ми множимо число на\(1\), в результаті виходить одне і те ж число. Що відбувається, коли ми помножимо число на\(−1\)? Давайте помножимо додатне число, а потім негативне число на,\(−1\) щоб побачити, що ми отримуємо.
\[\begin{array} {lll} {} &{-1\cdot 4} &{-1(-3)}\\ {\text{Multiply.}} &{-4} &{3} \\ {} &{-4\text{ is the opposite of 4.}} &{3\text{ is the opposite of } -3} \end{array}\]
Кожен раз, коли ми множимо число на\(−1\), ми отримуємо його протилежність!
МНОЖЕННЯ НА −1
\[−1a=−a\]
Множення числа на\(−1\) дає його протилежність.
Помножити:
- \(-1 \cdot 7\)
- \(-1(-11)\)
- Відповідь
-
- \[\begin{array} {ll} {} &{-1\cdot 7} \\ {\text{Multiply, noting that the signs are different}} &{-7} \\ {\text{so the product is negative.}} &{-7\text{ is the opposite of 7.}} \end{array}\]
- \[\begin{array} {ll} {} &{-1(-11)} \\ {\text{Multiply, noting that the signs are different}} &{11} \\ {\text{so the product is positive.}} &{11\text{ is the opposite of -11.}} \end{array}\]
Помножити:
- \(-1\cdot 9\)
- \(-1\cdot(-17)\)
- Відповідь
-
- \(-9\)
- \(17\)
Помножити:
- \(-1\cdot 8\)
- \(-1\cdot(-16)\)
- Відповідь
-
- \(-8\)
- \(16\)
Розділити цілі числа
А як щодо поділу? Ділення - обернена операція множення. Так,\(15\div 3=5\) тому що\(5 \cdot 3 = 15\). У словах цей вираз говорить, що\(15\) можна розділити на три групи по п'ять кожна, тому що додавання п'ять три рази дає\(15\). Подивіться на деякі приклади множення цілих чисел, щоб з'ясувати правила ділення цілих чисел.
\[\begin{array} {ll} {5\cdot 3 = 15\text{ so }15\div 3 = 5} &{-5(3) = -15\text{ so }-15\div 3 = -5} \\ {(-5)(-3) = 15\text{ so }15\div (-3) = -5} &{5(-3) = -15\text{ so }-15\div (-3) = 5} \end{array}\]
Ділення дотримується тих же правил, що і множення!
Для поділу двох знакових чисел, коли:
- ознаки однакові, частка позитивна.
- ознаки різні, частка негативна.
І пам'ятайте, що ми завжди можемо перевірити відповідь задачі поділу множенням.
Для множення та ділення двох знакових чисел:
- Якщо ознаки однакові, результат позитивний.
- Якщо ознаки різні, результат негативний.
| ті ж ознаки | Результат |
|---|---|
| Два позитиву | Позитивні |
| Два негативу | Позитивні |
| Якщо ознаки однакові, результат позитивний. | |
| Різні прикмети | Результат |
|---|---|
| Позитивні і негативні | Негативний |
| Негативні і позитивні | Негативний |
| Якщо ознаки різні, результат негативний. | |
- \(-27\div 3\)
- \(-100\div (-4)\)
- Відповідь
-
- \[\begin{array} {ll} {} &{-27 \div 3} \\ {\text{Divide, with different signs, the quotient is}} &{-9} \\ {\text{negative.}} &{} \end{array}\]
- \[\begin{array} {ll} {} &{-100 \div (-4)} \\ {\text{Divide, with signs that are the same the}} &{25} \\ {\text{ quotient is negative.}} &{} \end{array}\]
Розділити:
- \(-42\div 6\)
- \(-117\div (-3)\)
- Відповідь
-
- \(-7\)
- \(39\)
Розділити:
- \(-63\div 7\)
- \(-115\div (-5)\)
- Відповідь
-
- \(-9\)
- \(23\)
Спрощення виразів цілими числами
Що відбувається, коли у виразі більше двох чисел? Порядок операцій все ще застосовується при включенні негативів. Пам'ятаєте мою дорогу тітку Саллі?
Спробуємо кілька прикладів. Ми спростимо вирази, які використовують усі чотири операції з цілими числами - додавання, віднімання, множення та ділення. Не забувайте стежити за порядком операцій.
Спростити:
\(7(-2)+4(-7)-6\)
- Відповідь
-
\[\begin{array} {ll} {} &{7(-2)+4(-7)-6} \\ {\text{Multiply first.}} &{-14+(-28)-6} \\ {\text{Add.}} &{-42-6} \\{\text{Subtract}} &{-48} \end{array}\]
Спростити:
\(8(-3)+5(-7)-4\)
- Відповідь
-
\(-63\)
Спростити:
\(9(-3)+7(-8)-1\)
- Відповідь
-
\(-84\)
Спростити:
- \((-2)^{4}\)
- \(-2^{4}\)
- Відповідь
-
- \[\begin{array} {ll} {} &{(-2)^{4}} \\ {\text{Write in expanded form.}} &{(-2)(-2)(-2)(-2)} \\ {\text{Multiply}} &{4(-2)(-2)} \\{\text{Multiply}} &{-8(-2)} \\{\text{Multiply}} &{16} \end{array}\]
- \[\begin{array} {ll} {} &{-2^{4}} \\ {\text{Write in expanded form. We are asked to find the opposite of }2^{4}.} &{-(2\cdot 2\cdot 2 \cdot 2)} \\ {\text{Multiply}} &{-(4\cdot 2\cdot 2)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Multiply}} &{-16} \end{array}\]
Зверніть увагу на різницю частин (1) і (2). У частині (1) показник означає підняти те, що знаходиться в дужках,\((−2)\) до\(4^{th}\) влади. У частині (2), показник означає підняти тільки до\(4^{th}\) влади, а потім прийняти протилежне.\(2\)
Спростити:
- \((-3)^{4}\)
- \(-3^{4}\)
- Відповідь
-
- \(81\)
- \(-81\)
Спростити:
- \((-7)^{2}\)
- \(-7^{2}\)
- Відповідь
-
- \(49\)
- \(-49\)
Наступний приклад нагадує нам спочатку спростити внутрішні дужки.
Спростити:
\(12-3(9 - 12)\)
- Відповідь
-
\[\begin{array} {llll} {} &{12-3(9 - 12)} \\ {\text{Subtract parentheses first}} &{12-3(-3)} \\ {\text{Multiply.}} &{12-(-9)} \\{\text{Multiply}} &{-(8\cdot 2)} \\{\text{Subtract}} &{21} \end{array}\]
Спростити:
\(17 - 4(8 - 11)\)
- Відповідь
-
\(29\)
Спростити:
\(16 - 6(7 - 13)\)
- Відповідь
-
\(52\)
Спростити:
\(8(-9)\div (-2)^{3}\)
- Відповідь
-
\[\begin{array} {ll} {} &{8(-9)\div(-2)^{3}} \\ {\text{Exponents first}} &{8(-9)\div(-8)} \\ {\text{Multiply.}} &{-72\div (-8)} \\{\text{Divide}} &{9} \end{array}\]
Спростити:
\(12(-9)\div (-3)^{3}\)
- Відповідь
-
\(4\)
Спростити:
\(18(-4)\div (-2)^{3}\)
- Відповідь
-
\(9\)
Спростити:
\(-30\div 2 + (-3)(-7)\)
- Відповідь
-
\[\begin{array} {ll} {} &{-30\div 2 + (-3)(-7)} \\ {\text{Multiply and divide left to right, so divide first.}} &{-15+(-3)(-7)} \\ {\text{Multiply.}} &{-15+ 21} \\{\text{Add}} &{6} \end{array}\]
Спростити:
\(-27\div 3 + (-5)(-6)\)
- Відповідь
-
\(21\)
Спростити:
\(-32\div 4 + (-2)(-7)\)
- Відповідь
-
\(6\)
Оцінити змінні вирази з цілими числами
Пам'ятайте, що оцінювати вираз означає підставити число для змінної у виразі. Тепер ми можемо використовувати як негативні числа, так і позитивні числа.
Коли\(n=−5\), оцініть:
- \(n+1\)
- \(−n+1\).
- Відповідь
-
- \[\begin{array} {ll} {} &{n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-5+1} \\ {\text{Simplify.}} &{-4} \end{array}\]
- \[\begin{array} {ll} {} &{-n+ 1} \\ {\text{Substitute}-5\text{ for } n} &{-(-5)+1} \\ {\text{Simplify.}} &{-4} \\{\text{Add.}} &{6} \end{array}\]
Коли\(n=−8\), оцініть:
- \(n+2\)
- \(−n+2\).
- Відповідь
-
- \(-6\)
- \(10\)
Коли\(y=−9\), оцініть:
- \(y+8\)
- \(−y+8\).
- Відповідь
-
- \(-1\)
- \(17\)
Оцініть\((x+y)^{2}\), коли\(x = -18\) і\(y = 24\).
- Відповідь
-
\[\begin{array} {ll} {} &{(x+y)^{2}} \\ {\text{Substitute }-18\text{ for }x \text{ and } 24 \text{ for } y} &{(-18 + 24)^{2}} \\ {\text{Add inside parentheses}} &{(6)^{2}} \\{\text{Simplify.}} &{36} \end{array}\]
Оцініть\((x+y)^{2}\), коли\(x = -15\) і\(y = 29\).
- Відповідь
-
\(196\)
Оцініть\((x+y)^{3}\), коли\(x = -8\) і\(y = 10\).
- Відповідь
-
\(8\)
Оцініть\(20 -z \), коли
- \(z = 12\)
- \(z = -12\)
- Відповідь
-
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }12\text{ for }z.} &{20 - 12} \\ {\text{Subtract}} &{8} \end{array}\]
- \[\begin{array} {ll} {} &{20 - z} \\ {\text{Substitute }-12\text{ for }z.} &{20 - (-12)} \\ {\text{Subtract}} &{32} \end{array}\]
Оцініть\(17 - k\), коли
- \(k = 19\)
- \(k = -19\)
- Відповідь
-
- \(-2\)
- \(36\)
Оцініть\(-5 - b\), коли
- \(b = 14\)
- \(b = -14\)
- Відповідь
-
- \(-19\)
- \(9\)
Оцініть:
\(2x^{2} + 3x + 8\)коли\(x = 4\).
- Відповідь
-
Замінник\(4\) для\(x\). Використовуйте дужки, щоб показати множення.
\[\begin{array} {ll} {} &{2x^{2} + 3x + 8} \\ {\text{Substitute }} &{2(4)^{2} + 3(4) + 8} \\ {\text{Evaluate exponents.}} &{2(16) + 3(4) + 8} \\ {\text{Multiply.}} &{32 + 12 + 8} \\{\text{Add.}} &{52} \end{array}\]
Оцініть:
\(3x^{2} - 2x + 6\)коли\(x =-3\).
- Відповідь
-
\(39\)
Оцініть:
\(4x^{2} - x - 5\)коли\(x = -2\).
- Відповідь
-
\(13\)
Перекладіть фрази на вирази з цілими числами
Наша попередня робота з перекладу англійської на алгебру також стосується фраз, які включають як позитивні, так і негативні числа.
Перекласти і спростити: сума\(8\) і\(−12\), збільшена на\(3\).
- Відповідь
-
\[\begin{array} {ll} {} &{\text{the } \textbf{sum} \text{of 8 and -12, increased by 3}} \\ {\text{Translate.}} &{[8 + (-12)] + 3} \\ {\text{Simplify. Be careful not to confuse the}} &{(-4) + 3} \\{\text{brackets with an absolute value sign.}} \\{\text{Add.}} &{-1} \end{array}\]
Перекласти і спростити: сума\(9\) і\(−16\), збільшена на\(4\).
- Відповідь
-
\((9 + (-16)) + 4 - 3\)
Перекласти і спростити: сума\(-8\) і\(−12\), збільшена на\(7\).
- Відповідь
-
\((-8 + (-12)) + 7 - 13\)
Коли ми вперше ввели символи операції, ми побачили, що вираз може читатися декількома способами. Вони перераховані на графіку нижче.
| \(a−b\) |
|---|
| \ (a−b\)» data-valign="top">\(a\) мінус\(b\) різниця\(a\) і\(b\) \(b\) віднімання від\(a\) \(b\) меншої ніж\(a\) |
Будьте обережні, щоб отримати a і b в правильному порядку!
Перекладіть, а потім спрощуйте
- різниця\(13\) і\(−21\)
- відняти\(24\) від\(−19\).
- Відповідь
-
- \[\begin{array} {ll} {} &{\text{the } \textbf{difference } \text{of 13 and -21}} \\ {\text{Translate.}} &{13 - (-21)} \\ {\text{Simplify.}} &{34} \end{array}\]
- \[\begin{array} {ll} {} &\textbf{subtract }24 \textbf{ from }-19 \\ {\text{Translate.}} &{-19 - 24} \\ {\text{Remember, subtract b from a means }a - b} &{} \\{\text{Simplify.}} &{-43} \end{array}\]
Перекладіть і спрощуйте
- різниця\(14\) і\(−23\)
- відняти\(21\) від\(−17\).
- Відповідь
-
- \(14 - (-23); 37\)
- \(-17 - 21; -38\)
Перекладіть і спрощуйте
- різниця\(11\) і\(−19\)
- відняти\(18\) від\(−11\).
- Відповідь
-
- \(11 - (-19); 30\)
- \(-11 - 18; -29\)
Знову ж таки, наша попередня робота з перекладу англійської на алгебру переходить до фраз, які включають як множення, так і ділення цілих чисел. Пам'ятайте, що ключове слово для множення - «продукт», а для ділення - «частка».
Перекласти на алгебраїчний вираз і спростити по можливості: твір\(−2\) і\(14\).
- Відповідь
-
\[\begin{array} {ll} {} &{\text{the product of }-2 \text{ and } 14} \\ {\text{Translate.}} &{(-2)(14)} \\{\text{Simplify.}} &{-28} \end{array}\]
Перекласти на алгебраїчний вираз і спростити по можливості: твір\(−5\) і\(12\).
- Відповідь
-
\(-5(12); -60\)
Перекласти на алгебраїчний вираз і спростити по можливості: твір\(8\) і\(-13\).
- Відповідь
-
\(-8(13); -104\)
Перекласти на алгебраїчний вираз і спростити, якщо можливо: частка\(−56\) і\(−7\).
- Відповідь
-
\[\begin{array} {ll} {} &{\text{the quotient of }-56 \text{ and } -7} \\ {\text{Translate.}} &{-56\div(-7)} \\{\text{Simplify.}} &{8} \end{array}\]
Перекласти на алгебраїчний вираз і спростити, якщо можливо: частка\(−63\) і\(−9\).
- Відповідь
-
\(-63\div (-9); 7\)
Перекласти на алгебраїчний вираз і спростити, якщо можливо: частка\(−72\) і\(−9\).
- Відповідь
-
\(-72\div (-9); 8\)
Використання цілих чисел у програмах
Ми намітимо план вирішення додатків. Важко щось знайти, якщо ми не знаємо, що ми шукаємо або як це назвати! Тому, коли ми вирішуємо додаток, нам спочатку потрібно визначити, що проблема просить нас знайти. Потім ми напишемо фразу, яка дає інформацію, щоб знайти її. Ми переведемо фразу в вираз, а потім спростимо вираз, щоб отримати відповідь. Нарешті, ми підсумовуємо відповідь у реченні, щоб переконатися, що це має сенс.
Як застосувати стратегію для вирішення програм з цілими числами
Температура в Урбані, штат Іллінойс одного ранку була\(11\) градусами. До середини дня температура опустилася до\(−9\) градусів. У чому полягала різниця ранкової та післяобідньої температур?
- Відповідь
-
Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі. Крок 2. Визначте, що нас просять знайти. різниця ранкової та післяобідньої температур Крок 3. Напишіть фразу, яка дає інформацію, щоб знайти її. різниця\(11\) і\(-9\) Крок 4. Переведіть словосполучення в вираз. \(11 - (-9)\) Крок 5. Спростити вираз. \(20\) Крок 6. Напишіть повне речення, яке відповідає на питання. Різниця температур становила 20 градусів.
Температура в Анкориджі, штат Аляска одного ранку була\(15\) градусами. До середини дня температура опустилася до\(30\) градусів морозу. Яка різниця в ранковій та післяобідній температурах?
- Відповідь
-
Різниця температур становила\(45\) градуси.
Температура в Денвері була\(−6\) градусами в обідній час. До заходу сонця температура опустилася до\(−15\) градусів. У чому полягала різниця в обідній і західній температурах?
- Відповідь
-
Різниця температур становила\(9\) градуси.
- Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі
- Визначте, що нас просять знайти.
- Напишіть фразу, яка дає інформацію, щоб знайти її.
- Переведіть словосполучення в вираз.
- Спростити вираз.
- Відповісти на питання повним реченням.
Футбольна команда «Мустанг» отримала три пенальті в третій чверті. Кожен пенальті давав їм втрату в п'ятнадцять ярдів. Яка кількість втрачених ярдів?
- Відповідь
-
Крок 1. Прочитайте проблему. Переконайтеся, що всі слова та ідеї зрозумілі. Крок 2. Визначте, що нас просять знайти. кількість втрачених ярдів Крок 3. Напишіть фразу, яка дає інформацію, щоб знайти її. тричі на\(15\) -ярд штраф Крок 4. Переведіть словосполучення в вираз. \(3(-15)\) Крок 5. Спростити вираз. \(-45\) Крок 6. Напишіть повне речення, яке відповідає на питання. Команда втратила\(45\) двори.
Ведмеді грали погано і мали сім пенальті в грі. Кожен штраф призвів до втрати\(15\) ярдів. Яка кількість ярдів втрачено через штрафні санкції?
- Відповідь
-
Ведмеді втратили\(105\) двори.
Білл використовує банкомат на кампусі, тому що це зручно. Однак кожен раз, коли він ним користується, йому стягується плата в розмірі 2 долари. Минулого місяця він користувався банкоматом вісім разів. Скільки склала його загальна плата за користування банкоматом?
- Відповідь
-
З його розрахункового рахунку було віднімано комісію в розмірі 16 доларів.
Ключові поняття
- Множення та ділення двох знакових чисел
- Ті ж ознаки - товар позитивний
- Різні ознаки - продукт негативний
- Стратегія для додатків
- Визначте, що вас просять знайти.
- Напишіть фразу, яка дає інформацію, щоб знайти її.
- Переведіть словосполучення в вираз.
- Спростити вираз.
- Відповісти на питання повним реченням.
