Skip to main content
LibreTexts - Ukrayinska

1.9: Реальні числа

  1. Last updated
  2. Save as PDF
  • Page ID
    59059

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Цілі навчання

    До кінця цього розділу ви зможете:

    • Спростіть вирази за допомогою квадратних коренів
    • Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел
    • Знайдіть дроби на числовому рядку
    • Знайдіть десяткові знаки на числовому рядку
    Примітка

    Більш ретельне ознайомлення з темами, розглянутими в цьому розділі, можна знайти в розділах Преалгебри, Десяткові числа та властивості дійсних чисел.

    Спрощення виразів за допомогою квадратних коренів

    Пам'ятайте, що коли число множиться\(n\) саме на себе, ми пишемо\(n^{2}\) і читаємо його «в\(n\) квадрат». Отриманий результат називається квадратом\(n\). Наприклад,

    \[\begin{array} { l l } { 8 ^ { 2 } } & { \text { read '8 squared' } } \\ { 64 } & { 64 \text { is called the square of } 8 \text { . } } \end{array}\]

    Аналогічно 121 - це квадрат 11, тому що\(11^{2}\) дорівнює 121.

    КВАДРАТ ЧИСЛА

    Якщо\(n^{2}=m\), то\(m\) це квадрат\(n\).

    Примітка

    Виконання діяльності з маніпулятивної математики «Квадратні числа» допоможе вам розвинути краще розуміння ідеальних квадратних чисел.

    Заповніть наступну таблицю, щоб показати квадрати підрахунку чисел від 1 до 15.

    Є таблиця з двома рядками і 17 стовпцями. Перший ряд читається зліва направо Число, n, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14 і 15. Другий рядок читається зліва направо Квадрат, п квадрат, порожній, порожній, порожній, порожній, порожній, порожній, порожній, 64, порожній, порожній, порожній, 121, порожній, порожній, порожній і порожній.
    Малюнок\(\PageIndex{1}\)

    Числа у другому рядку називаються ідеальними квадратними числами. Корисно буде навчитися розпізнавати ідеальні квадратні числа.

    Квадрати рахункових чисел є додатними числами. А як щодо квадратів від'ємних чисел? Ми знаємо, що коли знаки двох чисел однакові, їх твір позитивний. Таким чином, квадрат будь-якого негативного числа також позитивний.

    \[( - 3 ) ^ { 2 } = 9 \quad ( - 8 ) ^ { 2 } = 64 \quad ( - 11 ) ^ { 2 } = 121 \quad ( - 15 ) ^ { 2 } = 225\]

    Ви помітили, що ці квадрати такі ж, як квадрати позитивних чисел?

    Іноді нам потрібно буде дивитися на зв'язок між числами і їх квадратами навпаки. Тому що\(10^{2}=100\), ми говоримо, 100 - це квадрат 10. Ми також говоримо, що 10 - це квадратний корінь 100. Число, квадрат якого дорівнює мм, називається квадратним коренем\(m\).

    КВАДРАТНИЙ КОРІНЬ ЧИСЛА

    Якщо\(n^{2}=m\), то\(n\) це квадратний корінь з\(m\).

    Зверніть увагу\((−10)^{2}=100\) також, так само\(−10\) є квадратний корінь\(100\). Тому обидва\(10\) і\(−10\) є квадратними корінням\(100\).

    Отже, кожне додатне число має два квадратних кореня - один позитивний і один негативний. Що робити, якщо ми хотіли тільки позитивний квадратний корінь позитивного числа? Радикальний знак,\(\sqrt{m}\), позначає позитивний квадратний корінь. Позитивний квадратний корінь називається основним квадратним коренем. Коли ми використовуємо радикальний знак, який завжди означає, що ми хочемо основний квадратний корінь.

    Ми також використовуємо знак радикала для квадратного кореня нуля. Тому що\(0^{2}=0, \sqrt{0}=0\). Зверніть увагу, що нуль має тільки один квадратний корінь.

    ПОЗНАЧЕННЯ КВАДРАТНОГО КОРЕНЯ

    \(\sqrt{m}\)читається «квадратний корінь\(m\)»

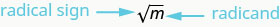
    Дається квадратний корінь, стрілкою до знаку радикала (він виглядає як галочка з горизонтальною лінією, що йде від його довгого кінця) позначається знак радикала і стрілкою до числа під знаком радикала, яка позначена радикандом.

    Якщо\(m = n^{2}\), то\(\sqrt{m} = n\), для\(n\geq 0\).

    Квадратний корінь\(m\),\(\sqrt{m}\), - додатне число, квадрат якого дорівнює\(m\).

    Оскільки 10 - основний квадратний корінь 100, ми пишемо\(\sqrt{100}=10\). Можливо, ви захочете заповнити наступну таблицю, щоб допомогти вам розпізнати квадратні корені.

    Є таблиця з двома рядками і 15 стовпцями. Перший рядок читає зліва направо квадратний корінь 1, квадратний корінь з 4, квадратний корінь з 9, квадратний корінь з 16, квадратний корінь 25, квадратний корінь 36, квадратний корінь з 49, квадратний корінь 64, квадратний корінь з 81, квадратний корінь 100, квадратний корінь 121, квадратний корінь 144, квадратний корінь 169, квадратний корінь з 196, і квадратний корінь 225. Другий ряд складається з усіх заготовок, крім десятої клітини під квадратний корінь 100, яка читається 10.
    Малюнок\(\PageIndex{2}\)
    Вправа\(\PageIndex{1}\)

    Спростити:

    1. \(\sqrt{25}\)
    2. \(\sqrt{121}\)
    Відповідь
    1. \[\begin{array} {ll} {} &{\sqrt{25}} \\ {\text {Since }5^{2} = 25} &{5} \end{array}\]
    2. \[\begin{array} {ll} {} &{\sqrt{121}} \\ {\text {Since }11^{2} = 121} &{11} \end{array}\]
    Вправа\(\PageIndex{2}\)

    Спростити:

    1. \(\sqrt{36}\)
    2. \(\sqrt{169}\)
    Відповідь
    1. 6
    2. 13
    Вправа\(\PageIndex{3}\)

    Спростити:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Відповідь
    1. 4
    2. 14

    Ми знаємо, що кожне позитивне число має два квадратних кореня, а знак радикалу вказує на позитивний. Пишемо\(\sqrt{100)=10\). Якщо ми хочемо знайти негативний квадратний корінь числа, ми ставимо негативний перед знаком радикала. Наприклад,\(-\sqrt{100)=-10\). Читаємо\(-\sqrt{100)\) як «протилежність квадратному кореню з 10».

    Вправа\(\PageIndex{4}\)

    Спростити:

    1. \(-\sqrt{9}\)
    2. \(-\sqrt{144}\)
    Відповідь
    1. \[\begin{array} {ll} {} &{-\sqrt{9}} \\ {\text {The negative is in front of the radical sign.}} &{-3} \end{array}\]
    2. \[\begin{array} {ll} {} &{-\sqrt{144}} \\ {\text {The negative is in front of the radical sign.}} &{-12} \end{array}\]
    Вправа\(\PageIndex{5}\)

    Спростити:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Відповідь
    1. −2
    2. −15
    Вправа\(\PageIndex{6}\)

    Спростити:

    1. \(\sqrt{16}\)
    2. \(\sqrt{196}\)
    Відповідь
    1. −9
    2. −10

    Визначення цілих чисел, раціональних чисел, ірраціональних чисел та дійсних чисел

    Ми вже описували числа як підрахунок чисел s, цілих чисел s та цілих чисел. У чому різниця між цими типами чисел?

    \[\begin{array} { l l } { \text { Counting numbers } } & { 1,2,3,4 , \ldots } \\ { \text { Whole numbers } } & { 0,1,2,3,4 , \ldots } \\ { \text { Integers } } & { \dots - 3 , - 2 , - 1,0,1,2,3 , \ldots } \end{array}\]

    Який тип чисел ми отримаємо, якби ми почали з усіх цілих чисел, а потім включили всі дроби? Числа, які ми мали б, утворюють набір раціональних чисел. Раціональне число - це число, яке можна записати у вигляді співвідношення двох цілих чисел.

    РАЦІОНАЛЬНЕ ЧИСЛО

    Раціональне число - це число виду\(\dfrac{p}{q}\), де p і q - цілі числа і\(q \neq 0\)

    Раціональне число можна записати як співвідношення двох цілих чисел.

    Всі підписані дроби, такі як\(\dfrac{4}{5}\),,\(-\dfrac{7}{8}\)\(\dfrac{13}{4}\),\(-\dfrac{20}{3}\) є раціональними числами. Кожен чисельник і кожен знаменник є цілим числом.

    Цілі числа є раціональними числами? Щоб вирішити, чи є ціле число раціональним числом, спробуємо записати його у вигляді співвідношення двох цілих чисел. Кожне ціле число може бути записано у вигляді співвідношення цілих чисел різними способами. Наприклад, 3 еквівалентно\(\dfrac{3}{1}\),\(-\dfrac{6}{2}\),\(\dfrac{9}{3}\),\(\dfrac{12}{4}\),\(-\dfrac{15}{5} \ldots\)

    Простий спосіб записати ціле число як співвідношення цілих чисел - записати його як дріб із знаменником один.

    \[3 = \frac { 3 } { 1 } \quad - 8 = - \frac { 8 } { 1 } \quad 0 = \frac { 0 } { 1 }\]

    Оскільки будь-яке ціле число можна записати як співвідношення двох цілих чисел, всі цілі числа є раціональними числами! Пам'ятайте, що підрахунок чисел і цілих чисел також є цілими числами, і тому вони теж раціональні.

    А як щодо десяткових знаків? Чи раціональні вони? Давайте подивимося на кілька, щоб побачити, якщо ми можемо написати кожен з них як співвідношення двох цілих чисел.

    Ми вже бачили, що цілі числа є раціональними числами. Ціле число\(−8\) можна записати як десяткове число\(−8.0\). Отже, зрозуміло, деякі десяткові знаки раціональні.

    Подумайте про десяткове число\(7.3\). Чи можемо ми записати його як співвідношення двох цілих чисел? Тому що\(7.3\) означає\(7\dfrac{3}{10}\), що ми можемо записати його як неправильний дріб,\(\dfrac{73}{10}\). Так\(7.3\) і співвідношення цілих чисел\(73\) і\(10\). Це раціональне число.

    Загалом, будь-яке десяткове число, яке закінчується після ряду цифр (наприклад,\(7.3\) або\(−1.2684\)), є раціональним числом. Ми можемо використовувати місце останньої цифри як знаменник при записі десяткового дробу.

    Вправа\(\PageIndex{7}\)

    Запишіть як співвідношення двох цілих чисел:

    1. −27
    2. 7.31
    Відповідь
    1. \[\begin{array} {ll} {} &{-27} \\ {\text {Write it as a fraction with denominator 1.}} &{\dfrac{-27}{1}} \end{array}\]
    2. \[\begin{array} {ll} {} &{7.31} \\ {\text {Write is as a mixed number. Remember.}} &{} \\ {\text {7 is the whole number and the decimal}} &{7\dfrac{31}{100}} \\ {\text {part, 0.31, indicates hundredths.}} &{} \\ {\text{Convert to an improper fraction.}} &{\dfrac{731}{100}} \end{array}\]

    Отже, ми бачимо, що −27 і 7.31 є раціональними числами, оскільки вони можуть бути записані як співвідношення двох цілих чисел.

    Вправа\(\PageIndex{8}\)

    Запишіть як співвідношення двох цілих чисел:

    1. −24
    2. 3.57
    Відповідь
    1. \(\dfrac{-24}{1}\)
    2. \(\dfrac{357}{100}\)
    Вправа\(\PageIndex{9}\)

    Запишіть як співвідношення двох цілих чисел:

    1. −19
    2. 8.41
    Відповідь
    1. \(\dfrac{-19}{1}\)
    2. \(\dfrac{841}{100}\)
    Давайте розглянемо десяткову форму чисел, які ми знаємо, є раціональними.

    Ми бачили, що кожне ціле число є раціональним числом, так як\(a = \dfrac{a}{1}\) для будь-якого цілого числа,\(a\). Ми також можемо змінити будь-яке ціле число до десяткової, додавши десяткову крапку і нуль.

    \[\begin{array} { l l l l l l l } { \text { Integer } } & { - 2 } & { - 1 } & { 0 } & { 1 } & { 2 } & { 3 } \\ { \text { Decimal form } } & { - 2.0 } & { - 1.0 } & { 0.0 } & { 1.0 } & { 2.0 } & { 3.0 } \\ { } & { \text { These decimal numbers stop. } } \end{array}\]

    Ми також бачили, що кожен дріб є раціональним числом. Подивіться на десяткову форму дробів, які ми розглянули вище.

    \[\begin{array} { l l l l } { \text { Ratio of integers } } & { \frac { 4 } { 5 } } & { - \frac { 7 } { 8 } } & { \frac { 13 } { 4 } } & { - \frac { 20 } { 3 } } \\ { \text { The decimal form } } & { 0.8 } & { - 0.875 } & { 3.25 } & { - 6.666 \dots } \\ { } & { } & { } & { - 6.\overline{6} } \\ { } & { \text { These decimal either stop or repeat. } } \end{array}\]

    Про що нам говорять ці приклади?

    Кожне раціональне число можна записати як у вигляді співвідношення цілих чисел\(\dfrac{p}{q}\), (, де p і q - цілі числа і\(q\neq 0\)), так і як десяткове число, яке зупиняється або повторюється.

    Ось числа, які ми розглядали вище, виражені у вигляді співвідношення цілих чисел і як десяткове:

    Дроби Цілі числа
    Число \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) −2 −1 0 1 2 3
    Співвідношення цілих чисел \(\frac{4}{5}\) \(\frac{7}{8}\) \(\frac{13}{4}\) \(-\frac{20}{3}\) \(-\frac{2}{1}\) \(-\frac{1}{1}\) \(\frac{0}{1}\) \(\frac{1}{1}\) \(\frac{2}{1}\) \(\frac{3}{1}\)
    Десяткова форма 0.8 −0,875 3.25 \(−6.\overline{6}\) −2.0 −1.0 0.0 1.0 2.0 3.0
    Таблиця\(\PageIndex{1}\)
    РАЦІОНАЛЬНЕ ЧИСЛО

    Раціональне число - це число виду\(\frac{p}{q}\), де p і q - цілі числа і\(q\neq 0\)

    Його десяткова форма зупиняється або повторюється.

    Чи є десяткові знаки, які не зупиняються і не повторюються? Так!

    Число\(\pi\) (грецька буква пі, вимовляється «пиріг»), яке дуже важливо при описі кіл, має десяткову форму, яка не зупиняється і не повторюється.

    \[\pi =3.141592654\ldots\]

    Ми навіть можемо створити десятковий шаблон, який не зупиняється і не повторюється, наприклад

    \[2.01001000100001\ldots\]

    Числа, десяткова форма яких не зупиняється або повторюється, не можна записати як дріб цілих чисел. Ми називаємо ці цифри нераціональними.

    ІРРАЦІОНАЛЬНЕ ЧИСЛО

    Ірраціональне число - це число, яке не можна записати як співвідношення двох цілих чисел.

    Його десяткова форма не зупиняється і не повторюється.

    Давайте підсумуємо метод, який ми можемо використовувати, щоб визначити, чи є число раціональним чи ірраціональним.

    РАЦІОНАЛЬНИЙ ЧИ ІРРАЦІОНАЛЬНИЙ?

    Якщо десяткова форма числа

    • повторюється або зупиняється, число раціональне.
    • не повторюється і не зупиняється, число нераціональне.
    Вправа\(\PageIndex{10}\)

    З урахуванням чисел\(0.58\overline{3}, 0.47, 3.605551275\ldots\) переліку

    1. раціональні числа
    2. ірраціональні числа.
    Відповідь
    1. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{\text{The 3 repeats in }0.58\overline{3}.} \\ {} &{\text {The decimal 0.47 stops after the 7.}}\\ {} &{\text {So } 0.58\overline{3} \text{ and } 0.47 \text{are rational}} \end{array}\]
    2. \[\begin{array} {ll} {\text{Look for decimals that repeat or stop}} &{3.605551275\ldots\text{has no repeating block of}} \\ {} &{\text {digits and it does not stop.}}\\ {} &{\text {So } 3.605551275\ldots \text{ is irrational.}} \end{array}\]
    Вправа\(\PageIndex{11}\)

    Для заданих номерів перерахуйте

    1. раціональні числа
    2. ірраціональні числа:\(0.29, 0.81\overline{6}, 2.515115111….\)
    Відповідь
    1. \(0.29, 0.81\overline{6}\)
    2. \(2.515115111….\)
    Вправа\(\PageIndex{12}\)

    Для заданих номерів перерахуйте

    1. раціональні числа
    2. ірраціональні числа:\(2.6\overline{3}, 0.125, 0.418302…\)
    Відповідь
    1. \(2.6\overline{3}, 0.125\)
    2. \(0.418302…\)
    Вправа\(\PageIndex{13}\)

    Для кожного наведеного числа визначте, чи є воно раціональним чи ірраціональним:

    1. \(\sqrt{36}\)
    2. \(\sqrt{44}\)
    Відповідь
    1. Визнайте, що 36 - ідеальний квадрат, оскільки\(6^{2} = 36\). Отже\(\sqrt{36} = 6\), тому\(\sqrt{36}\) є раціональним.
    2. Пам'ятайте, що\(6^{2} = 36\) і\(7^{2} = 49\),\(44\) так не ідеальний квадрат. Тому десяткова форма ніколи не\(\sqrt{44}\) повторюватиметься і ніколи не\(\sqrt{44}\) зупиняється, так само нераціонально.
    Вправа\(\PageIndex{14}\)

    Для кожного наведеного числа визначте, чи є воно раціональним чи ірраціональним:

    1. \(\sqrt{81}\)
    2. \(\sqrt{17}\)
    Відповідь
    1. раціональні
    2. ірраціональний
    Вправа\(\PageIndex{15}\)

    Для кожного наведеного числа визначте, чи є воно раціональним чи ірраціональним:

    1. \(\sqrt{116}\)
    2. \(\sqrt{121}\)
    Відповідь
    1. ірраціональний
    2. раціональні

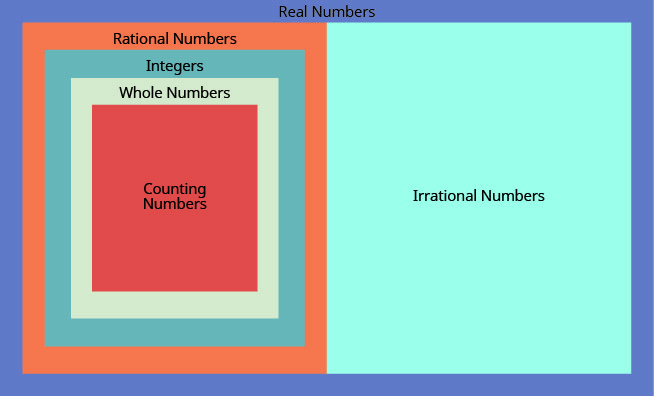
    Ми бачили, що всі числа підрахунку є цілими числами, всі цілі числа цілі числа, а всі цілі числа - раціональні числа. Ірраціональні числа - це числа, десяткова форма яких не зупиняється і не повторюється. Коли ми збираємо раціональні числа і ірраціональні числа, ми отримуємо безліч дійсних чисел s.

    РЕАЛЬНЕ ЧИСЛО

    Реальне число - це число, яке є або раціональним, або ірраціональним.

    Всі числа, які ми використовуємо в елементарній алгебрі, є дійсними числами. Малюнок\(\PageIndex{3}\) ілюструє, як набори чисел, які ми обговорювали в цьому розділі, поєднуються між собою.

    Ця цифра складається з діаграми Венна. Для початку є великий прямокутник з позначкою Real Numbers. Права половина прямокутника складається з ірраціональних чисел. Ліва половина складається з раціональних чисел. У прямокутнику раціональних чисел є цілі числа..., від'ємні 2, від'ємні 1, 0, 1, 2,... У прямокутнику цілих чисел є цілі числа 0, 1, 2, 3,... У прямокутнику цілих чисел є підрахунок чисел 1, 2, 3,...
    Малюнок\(\PageIndex{3}\): Ця діаграма показує набори чисел, що складають набір дійсних чисел. Чи здається вам дивним термін «реальні цифри»? Чи є цифри, які не є «реальними», і якщо так, то якими вони можуть бути?

    Чи можемо ми спростити\(\sqrt{-25}\)? Чи є число, квадрат якого\(−25\)?

    \[(\quad)^{2}=−25?\]

    Жодне з чисел, з якими ми мали справу до цих пір, не має квадрата, який є\(−25\). Чому? Будь-яке додатне число в квадраті є позитивним. Будь-яке негативне число в квадраті є позитивним. Таким чином, ми говоримо, що немає реального числа, рівного\(\sqrt{-25}\).

    Квадратний корінь від'ємного числа не є дійсним числом.

    Вправа\(\PageIndex{16}\)

    Для кожного заданого числа визначте, чи є це дійсним числом чи ні дійсним числом:

    1. \(\sqrt{-169}\)
    2. \(-\sqrt{64}\)
    Відповідь
    1. Немає дійсного числа, квадрат якого дорівнює\(−169\). Тому не\(\sqrt{-169}\) є дійсним числом.
    2. Так як негатив знаходиться перед радикалом,\(-\sqrt{64}\) є\(−8\), Так як\(−8\) є дійсним числом,\(-\sqrt{64}\) є дійсним числом.
    Вправа\(\PageIndex{17}\)

    Для кожного заданого числа визначте, чи є це дійсним числом чи ні дійсним числом:

    1. \(\sqrt{-196}\)
    2. \(-\sqrt{81}\)
    Відповідь
    1. не дійсне число
    2. дійсне число
    Вправа\(\PageIndex{18}\)

    Для кожного заданого числа визначте, чи є це дійсним числом чи ні дійсним числом:

    1. \(-\sqrt{49}\)
    2. \(\sqrt{-121}\)
    Відповідь
    1. дійсне число
    2. не дійсне число
    Вправа\(\PageIndex{19}\)

    З огляду на цифри\(−7, \frac{14}{5}, 8, \sqrt{5}, 5.9, \sqrt{64}\), перерахуйте

    1. цілих чисел
    2. цілих чисел
    3. раціональні числа
    4. ірраціональні числа
    5. дійсні числа
    Відповідь
    1. Пам'ятайте, цілі числа 0, 1, 2, 3,... і 8 - єдине ціле число.
    2. Цілі числа - це цілі числа, їх протилежності та 0. Таким чином, ціле число 8 є цілим числом, а −7 протилежне цілому числу, тому воно теж є цілим числом. Крім того, зверніть увагу, що 64 квадрат 8 так\(-\sqrt{64} = -8\). Таким чином, цілі числа є\(−7, 8, \sqrt{64}\).
    3. Так як всі цілі числа раціональні, то\(-7, 8, -\sqrt{64}\) є раціональними. Раціональні числа також включають дробові та десяткові дроби, які повторюються або зупиняються, тому\(\frac{14}{5}\) і\(5.9\) є раціональними. Отже, список раціональних чисел\(−7, \frac{14}{5}, 8, 5.9, \sqrt{64}\)
    4. Пам'ятайте, що 5 - це не ідеальний квадрат,\(\sqrt{5}\) тому нераціонально.
    5. Всі перераховані цифри є дійсними числами.
    Вправа\(\PageIndex{20}\)

    Для заданих номерів перерахуйте

    1. цілих чисел
    2. цілих чисел
    3. раціональні числа
    4. ірраціональні числа
    5. дійсні числа:\(−3, -\sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Відповідь
    1. \(4, \sqrt{49}\).
    2. \(−3, 4, \sqrt{49}\)
    3. \(−3, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    4. \( -\sqrt{2}\)
    5. \(−3, \sqrt{2}, 0.\overline{3}, \frac{9}{5}, 4, \sqrt{49}\)
    Вправа\(\PageIndex{21}\)

    Для заданих номерів перерахуйте

    1. цілих чисел
    2. цілих чисел
    3. раціональні числа
    4. ірраціональні числа
    5. дійсні числа:\(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)
    Відповідь
    1. \(6, \sqrt{121}\).
    2. \(−\sqrt{25}, −1, 6, \sqrt{121}\)
    3. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}\)
    4. \(2.041975…\)
    5. \(−\sqrt{25},−\frac{3}{8}, −1, 6, \sqrt{121}, 2.041975…\)

    Знайдіть дроби на числовому рядку

    Останній раз, коли ми дивилися на числовий рядок, він мав тільки позитивні і негативні цілі числа на ньому. Тепер ми хочемо включити дріб s і десяткових знаків на ньому.

    Примітка

    Виконання діяльності з маніпулятивної математики «Числова лінія Частина 3» допоможе вам розвинути краще розуміння розташування дробів на числовій лінії.

    Давайте почнемо з дробів і знайдіть\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) і\(\frac{8}{3}\) на числовому рядку.

    Ми почнемо з цілих чисел 3 і −5. тому що їх найпростіше побудувати. Див\(\PageIndex{4}\). Малюнок.

    Правильні дроби перераховані є\(\frac{1}{5}\text{ and } -\frac{4}{5}\). Ми знаємо, що правильний дріб\(\frac{1}{5}\) має значення менше одиниці і так буде розташовуватися між 0 і 1. Знаменник дорівнює 5, тому ділимо одиницю від 0 до 1 на 5 рівних частин\(\frac{1}{5}, \frac{2}{5}, \frac{3}{5}, \frac{4}{5}\). Змова\(\frac{1}{5}\). Див\(\PageIndex{4}\). Малюнок.

    Аналогічно,\(-\frac{4}{5}\) знаходиться між 0 і −1. Після поділу одиниці на 5 рівних частин наносимо ділянку\(-\frac{4}{5}\). Див\(\PageIndex{4}\). Малюнок.

    Нарешті, подивіться на неправильні дроби\(\frac{7}{4}, -\frac{9}{2}, \frac{8}{3}\). Це дроби, в яких чисельник більше знаменника. Розташування цих точок може бути простіше, якщо змінити кожну з них на змішане число. Див\(\PageIndex{4}\). Малюнок.

    \[\frac { 7 } { 4 } = 1 \frac { 3 } { 4 } \quad - \frac { 9 } { 2 } = - 4 \frac { 1 } { 2 } \quad \frac { 8 } { 3 } = 2 \frac { 2 } { 3 }\]

    \(\PageIndex{4}\)На малюнку показана числова лінія з нанесеними всіма точками.

    Існує цифра, показана, яка проходить від негативних 6 до позитивних 6. Зліва направо позначені цифри - негативні 5, негативні 9/2, негативні 4/5, 1/5, 4/5, 8/3 та 3. Число негативне 9/2 знаходиться на півдорозі між негативними 5 і негативними 4. Число негативне 4/5 трохи праворуч від негативного 1. Число 1/5 знаходиться трохи праворуч від 0. Число 4/5 знаходиться трохи лівіше 1. Число 8/3 знаходиться між 2 і 3, але трохи ближче до 3.
    Малюнок\(\PageIndex{4}\)
    Вправа\(\PageIndex{22}\)

    Знайдіть і позначте на цифровому рядку наступне:\(4, \frac{3}{4}, -\frac{1}{4}, -3, \frac{6}{5}, -\frac{5}{2}\) і\(\frac{7}{3}\).

    Відповідь

    Знайдіть і побудуйте цілі числа, 4, −3.

    \(\frac{3}{4}\)Спочатку знайдіть правильний дріб. Дріб\(\frac{3}{4}\) знаходиться в межах від 0 до 1. Ділимо відстань між 0 і 1 на чотири рівні частини потім, намічаємо\(\frac{3}{4}\). Аналогічно сюжет\(-\frac{1}{4}\).

    Тепер знайдіть неправильні\(\frac{6}{5}\) дроби,\(-\frac{5}{2}\),\(\frac{7}{3}\). Їх простіше побудувати, якщо ми перетворимо їх у мішані числа, а потім побудуємо їх так, як описано вище:\(\frac{6}{5} = 1\frac{1}{5}\),\(-\frac{5}{2} = -2\frac{1}{2}\),\(\frac{7}{3} = 2\frac{1}{3}\).

    Існує цифра, показана, яка проходить від негативних 6 до позитивних 6. Зліва направо позначені цифри - негативні 3, негативні 5/2, негативні 1/4, 3/4, 6/5, 7/3 та 4. Число від'ємне 5/2 знаходиться на півдорозі між негативними 3 та негативними 2. Число негативне 1/4 знаходиться трохи лівіше 0. Число 3/4 знаходиться трохи лівіше 1. Число 6/5 знаходиться трохи праворуч від 1. Число 7/3 знаходиться між 2 і 3, але трохи ближче до 2.

    Вправа\(\PageIndex{23}\)

    Знайдіть і позначте на цифровому рядку наступне:\(-1, \frac{1}{3}, \frac{6}{5}, -\frac{7}{4}, \frac{9}{2}, 5\) і\(-\frac{8}{3}\).

    Відповідь

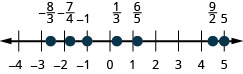
    Там показаний номер рядка, який проходить від негативних 4 до позитивних 5. Зліва направо позначені цифри - негативні 8/3, негативні 7/4, негативні 1, 1/3, 6/5, 9/2 та 5. Число негативне 8/3 знаходиться між негативними 3 і негативними 2, але трохи ближче до негативних 3. Число негативне 7/4 трохи праворуч від негативного 2. Число 1/3 знаходиться трохи праворуч від 0. Число 6/5 знаходиться трохи праворуч від 1. Число 9/2 знаходиться на півдорозі між 4 і 5.

    Вправа\(\PageIndex{24}\)

    Знайдіть і позначте на цифровому рядку наступне:\(\frac{1}{5}, -\frac{4}{5}, 3, \frac{7}{4}, -\frac{9}{2}, -5\) і\(\frac{8}{3}\).

    Відповідь

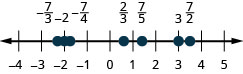
    Там показаний номер рядка, який проходить від негативних 4 до позитивних 5. Зліва направо позначені числа - негативні 7/3, негативні 2, негативні 7/4, 2/3, 7/5, 3 та 7/2. Число негативне 7/3 знаходиться між негативними 3 і негативними 2, але трохи ближче до негативних 2. Число негативне 7/4 трохи праворуч від негативного 2. Число 2/3 трохи лівіше 1. Число 7/5 знаходиться між 1 і 2, але ближче до 1. Число 7/2 знаходиться на півдорозі між 3 і 4.

    У\(\PageIndex{25}\) Вправі ми будемо використовувати символи нерівності для упорядкування дробів. У попередніх розділах ми використовували числовий рядок для замовлення чисел.

    • \(a < b\)«a менше b», коли a ліворуч від b на числовому рядку
    • \(a > b\)«a більше b», коли a знаходиться праворуч від b на числовому рядку

    Коли ми рухаємося зліва направо по числовому рядку, значення збільшуються.

    Вправа\(\PageIndex{25}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\). Може бути корисно звернутися до рис\(\PageIndex{5}\).

    1. \(−\frac{2}{3}\text{___}-1\)
    2. \(−3\frac{1}{2}\text{___}-3\)
    3. \(−\frac{3}{4}\text{___}-\frac{1}{4}\)
    4. \(−2\text{___}-\frac{8}{3}\)
    Там показаний номер рядка, який проходить від негативних 4 до позитивних 4. Зліва направо позначені числа - негативні 3 та 1/2, негативні 3, негативні 8/3, негативні 2, негативні 1, негативні 3/4, негативні 2/3 та негативні 1/4. Число негативне 3 та 1/2 знаходиться між негативними 4 та негативними 3 Число негативне 8/3 знаходиться між негативними 3 та негативними 2, але ближче до негативних 3. Числа від'ємні 3/4, від'ємні 2/3 та від'ємні 1/4 знаходяться між негативними 1 і 0.
    Малюнок\(\PageIndex{5}\)
    Відповідь

    Будьте уважні при замовленні негативних чисел.

    1. \(\begin{array} { r r } { } & { - \frac { 2 } { 3 } \text{ ___ } -1 } \\ { - \frac { 2 } { 3 } \text { is to the right of } - 1 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    2. \(\begin{array} { r r } { } & { - 3\frac { 1 } { 2 } \text{ ___ } -3 } \\ { - 3\frac { 1 } { 2 } \text { is to the right of } - 3 \text { on the number line. } } & { - \frac { 2 } { 3 } > - 1 } \end{array}\)
    3. \(\begin{array} { r r } { } & { - \frac { 3 } { 4 } \text{ ___ } -\frac{1}{4} } \\ { - \frac { 3 } { 4 } \text { is to the right of } - \frac{1}{4} \text { on the number line. } } & { - \frac{3}{4} < - \frac{1}{4} } \end{array}\)
    4. \(\begin{array} { r r } { } & { - \-2 \text{ ___ } -\frac{8}{3} } \\ { -2 \text { is to the right of } - \frac{8}{3} \text { on the number line. } } & { -2 > -\frac{8}{3} } \end{array}\)
    Вправа\(\PageIndex{26}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\).

    1. \(−\frac{1}{3}\text{___}-1\)
    2. \(−1\frac{1}{2}\text{___}-2\)
    3. \(−\frac{2}{3}\text{___}-\frac{1}{3}\)
    4. \(−3\text{___}-\frac{7}{3}\)
    Відповідь
    1. \(>\)
    2. \(>\)
    3. \(<\)
    4. \(<\)
    Вправа\(\PageIndex{27}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\).

    1. \(−1\text{___}-\frac{2}{3}\)
    2. \(−2\frac{1}{4}\text{___}-2\)
    3. \(−\frac{3}{5}\text{___}-\frac{4}{5}\)
    4. \(−4\text{___}-\frac{10}{3}\)
    Відповідь
    1. \(<\)
    2. \(<\)
    3. \(>\)
    4. \(<\)

    Знайдіть десяткові числа на цифровому рядку

    Оскільки десяткові числа є формами дробів, розташування десяткових знаків на числовому рядку аналогічно розташуванню дробів на числовому рядку.

    Вправа\(\PageIndex{28}\)

    Знайдіть 0.4 на цифровому рядку.

    Відповідь

    Правильний дріб має значення менше одиниці. Десяткове число\(0.4\) еквівалентно\(\frac{4}{10}\), правильний дріб, тому\(0.4\) знаходиться між 0 і 1. На числовому рядку розділіть інтервал між 0 і 1 на 10 рівних частин. Тепер маркуємо деталі\(0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0\). Ми пишемо 0 як 0.0 і 1 і 1.0, так що числа послідовно в десятих. Нарешті, позначте\(0.4\) на цифровому рядку. Див\(\PageIndex{6}\). Малюнок.

    Показано номер рядка, який працює від 0.0 до 1. Єдина надана точка - 0,4, що знаходиться в межах від 0,3 до 0,5.
    Малюнок\(\PageIndex{6}\)
    Вправа\(\PageIndex{29}\)

    Знайдіть на цифровому рядку: 0.6.

    Відповідь

    Показано номер рядка, який працює від 0.0 до 1. Єдина надана точка - 0,6, що знаходиться в межах від 0,5 до 0,7.

    Вправа\(\PageIndex{30}\)

    Знайдіть на цифровому рядку: 0.9.

    Відповідь

    Показано номер рядка, який працює від 0.0 до 1. Єдина надана точка - 0,9, що знаходиться між 0,8 і 1.

    Вправа\(\PageIndex{31}\)

    Знайдіть\(−0.74\) на цифровому рядку.

    Відповідь

    Десяткове значення (−0.74\) еквівалентно\(-\frac{74}{100}\), тому воно знаходиться між 0 і −1. На числовому рядку позначте і позначте соті в інтервалі між 0 і −1. Див\(\PageIndex{7}\). Малюнок.

    Показано номер рядка, який працює від негативного 1.00 до 0.00. Єдиним моментом є негативний 0,74, який знаходиться між негативними 0,8 і негативними 0,7.
    Малюнок\(\PageIndex{7}\)
    Вправа\(\PageIndex{32}\)

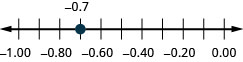
    Знайдіть у цифровому рядку: −0.6.

    Відповідь

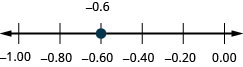
    Показано номер рядка, який працює від негативного 1.00 до 0.00. Єдиний момент - від'ємний 0.6, який знаходиться між негативними 0.8 і негативними 0.4.

    Вправа\(\PageIndex{33}\)

    Знайдіть у цифровому рядку: −0.7.

    Відповідь

    Показано номер рядка, який працює від негативного 1.00 до 0.00. Єдиний момент - від'ємний 0,7, який знаходиться між негативними 0,8 і негативними 0,6.

    Що більше, 0,04 або 0,40? Якщо ви вважаєте це грошима, ви знаєте, що 0,40 долара (сорок центів) більше, ніж 0,04 долара (чотири центи). Отже,\(0.40 > 0.04\)

    Знову ж таки, ми можемо використовувати номер рядка для замовлення номерів.

    • \(a < b\)«a менше b», коли a ліворуч від b на числовому рядку
    • \(a > b\)«a більше b», коли a знаходиться праворуч від b на числовому рядку

    Де на числовому рядку розташовані 0,04 і 0,40? Див\(\PageIndex{8}\). Малюнок.

    Показано номер рядка, який працює від від'ємного 0.0 до 1.0. Зліва направо відзначені точки 0,04 і 0,4. Точка 0,04 знаходиться між 0,0 і 0,1. Точка 0,4 знаходиться в межах від 0,3 до 0,5.
    Малюнок\(\PageIndex{8}\)

    Ми бачимо, що 0.40 знаходиться праворуч від 0.04 на числовому рядку. Це ще один спосіб продемонструвати це\(0.40 > 0.04\).

    Як 0.31 порівняно з 0.308? Це не перетворюється на гроші, щоб полегшити порівняння. Але якщо ми перетворимо 0.31 і 0.308 в дроби, ми можемо сказати, яка більше.

      0,31 0,308
    Перетворити на дроби. \(\frac{31}{100}\) \(\frac{308}{1000}\)
    Нам потрібен спільний знаменник, щоб порівняти їх. . .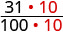
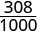      \(\frac{310}{1000}\) \(\frac{308}{1000}\)
    Таблиця\(\PageIndex{2}\)

    \(310 > 308\)Тому що ми це знаємо\(\frac{310}{1000} > \frac{308}{1000}\). Тому,\(0.31 > 0.308\).

    Зверніть увагу, що ми зробили при\(0.31\) перетворенні на дріб - ми почали з дробу\(\frac{31}{100}\) і закінчилися еквівалентним дробом\(\frac{310}{1000}\) .Перетворення\(\frac{310}{1000}\) назад в десятковий дає 0.310. Таким чином, 0,31 еквівалентно 0,310. Запис нулів в кінці десяткової коми не змінює його значення!

    \[\frac { 31 } { 100 } = \frac { 310 } { 1000 } \quad \text { and } \quad 0.31 = 0.310\]

    Ми говоримо, що 0.31 і 0.310 еквівалентні десяткових знаків.

    ЕКВІВАЛЕНТНІ ДЕСЯТКОВІ

    Два десяткових знака еквівалентні, якщо вони перетворюються на еквівалентні дроби.

    Ми використовуємо еквівалентні десяткові числа при замовленні десяткових знаків.

    Кроки, які ми робимо для замовлення десяткових знаків, узагальнені тут.

    ЗАМОВИТИ ДЕСЯТКОВІ ЗНАКИ.
    1. Запишіть цифри один під іншим, вишикуючи десяткові крапки.
    2. Перевірте, чи обидва числа мають однакову кількість цифр. Якщо ні, запишіть нулі в кінці одиниці з меншою кількістю цифр, щоб вони збігалися.
    3. Порівняйте числа так, ніби вони цілі числа.
    4. Впорядкуйте числа, використовуючи відповідний знак нерівності.
    Вправа\(\PageIndex{34}\)

    Замовлення\(0.64 \text{ ___ } 0.6\) за допомогою\(<\) або\(>\).

    Відповідь

    \(\begin{array} { ll } { \text {Write the numbers one under the other, } } &{0.64} \\ { \text {lining up the decimal points. } } &{0.6} \\ \\ { \text {Add a zero to 0.6 to make it a decimal } } &{0.64} \\ {\text{with 2 decimal places.}} &{0.60} \\ {\text{Now they are both hundredths.}} &{} \\ \\ {\text{64 is greater than 60.}} &{64 > 60} \\ \\ {\text{64 hundredths is greater than 60 hundredths.}} &{0.64 > 0.60} \\ \\ {} &{0.64 > 0.6}\end{array}\)

    Вправа\(\PageIndex{35}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):\(0.42 \text{ ___ } 0.4\).

    Відповідь

    \(>\)

    Вправа\(\PageIndex{36}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):\(0.18 \text{ ___ } 0.1\).

    Відповідь

    \(>\)

    Вправа\(\PageIndex{37}\)

    Замовлення\(0.83 \text{ ___ } 0.803\) за допомогою\(<\) або\(>\).

    Відповідь

    \(\begin{array} { ll } {} &{0.83\text{ ___ }0.803} \\ \\{ \text {Write the numbers one under the other, } } &{0.83} \\ { \text {lining up the decimal points. } } &{0.803} \\ \\ { \text {They do not have the same number of} } &{0.830} \\ {\text{digits.}} &{0.803} \\ {\text{Write one zero at the end of 0.83.}} &{} \\ \\ {\text{Since 830 > 803, 830 hundredths is}} &{0.830 > 0.803} \\ {\text{greater than 803 thousandths.}} &{}\\ \\ {} &{0.83 > 0.803}\end{array}\)

    Вправа\(\PageIndex{38}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):\(0.76 \text{ ___ } 0.706\).

    Відповідь

    \(>\)

    Вправа\(\PageIndex{39}\)

    Замовте кожну з наступних пар чисел, використовуючи\(<\) або\(>\):\(0.305 \text{ ___ } 0.35\).

    Відповідь

    \(<\)

    Коли ми замовляємо від'ємні десяткові числа, важливо пам'ятати, як впорядкувати від'ємні цілі числа. Нагадаємо, що більші числа знаходяться праворуч на числовому рядку. Наприклад, тому що −2 лежить праворуч від -3 на числовому рядку, ми знаємо, що\(−2>−3\). Аналогічно, менші числа лежать ліворуч на числовому рядку. Наприклад, оскільки −9 лежить ліворуч від −6 на числовому рядку, ми це знаємо\(−9<−6\). Див\(\PageIndex{9}\). Малюнок.

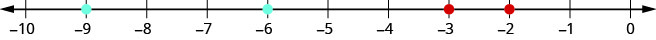
    Показано номер рядка, який проходить від негативних 10 до 0. Там не вказано точок, і хеш-мітки існують у кожному цілому числі між негативними 10 і 0.
    Малюнок\(\PageIndex{9}\)

    Якби ми збільшили інтервал між 0 і −1, як показано у\(\PageIndex{40}\) Вправі, ми побачили б так само, як\(−0.2>−0.3\) і\(−0.9<−0.6\).

    Вправа\(\PageIndex{40}\)

    Використовувати\(<\) або\(>\) замовляти\(−0.1\text{ ___ }−0.8\).

    Відповідь

    \(\begin{array} { ll } {} &{-0.1 \text{ ___ } -0.8} \\ \\ { \text { Write the numbers one under the other, lining up the } } &{-0.1} \\ { \text { decimal points. } } &{-0.8} \\ { \text { They have the same number of digits. } } &{} \\ \\ { \text { since } - 1 > - 8 , - 1 \text { tenth is greater than } - 8 \text { tenths. } } &{-0.1 > -0.8} \end{array}\)

    Вправа\(\PageIndex{41}\)

    Замовте наступну пару чисел, використовуючи\(<\) або\(>\):\(−0.3\text{ ___ }−0.5\).

    Відповідь

    \(>\)

    Вправа\(\PageIndex{42}\)

    Замовте наступну пару чисел, використовуючи\(<\) або\(>\):\(−0.6\text{ ___ }−0.7\).

    Відповідь

    \(>\)

    Ключові концепції

    • Позначення квадратного кореня
      \(\sqrt{m}\) читається «квадратний корінь»\(m\). Якщо\(m = n^{2}\), то\(\sqrt{m} = n\), для\(n \geq 0\).
    • Порядок десяткових знаків
      1. Запишіть цифри один під іншим, вишикуючи десяткові крапки.
      2. Перевірте, чи обидва числа мають однакову кількість цифр. Якщо ні, запишіть нулі в кінці одиниці з меншою кількістю цифр, щоб вони збігалися.
      3. Порівняйте числа так, ніби вони цілі числа.
      4. Впорядкуйте числа, використовуючи відповідний знак нерівності.

    Практика робить досконалим

    Спрощення виразів за допомогою квадратних коренів

    У наступних вправах спростити.