5.E: Поліноміальні функції (вправи)

5.1: Функції

У вправах 1-6 вкажіть область та діапазон заданого співвідношення.

1)$R=\{(7,4),(2,4),(4,2),(8,5)\}$

Відповідь

Домен$=\{2,4,7,8\}$ і діапазон$=\{2,4,5\}$

2)$S=\{(6,4),(3,3),(2,5),(8,7)\}$

3)$T=\{(7,2),(3,1),(9,4),(8,1)\}$

Відповідь

Домен$=\{3,7,8,9\}$ і діапазон$=\{1,2,4\}$

4)$R=\{(0,1),(8,2),(6,8),(9,3)\}$

5)$T=\{(4,7),(4,8),(5,0),(0,7)\}$

Відповідь

Домен$=\{0,4,5\}$ і діапазон$=\{0,7,8\}$

6)$T=\{(9,0),(3,6),(8,0),(3,8)\}$

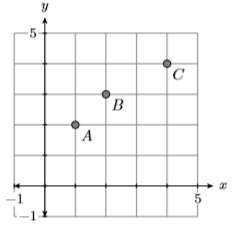
У Вправах 7-10 вкажіть область та діапазон заданого співвідношення.

7)

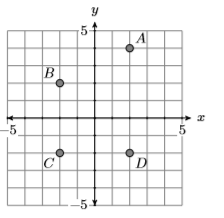
Відповідь

Домен$=\{-2,2\}$ і діапазон$=\{-2,2,4\}$

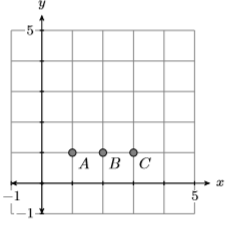
8)

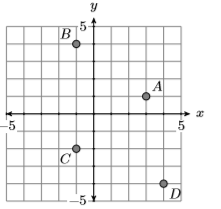
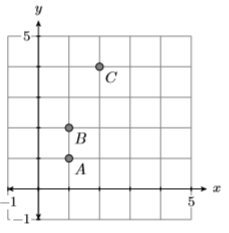
9)

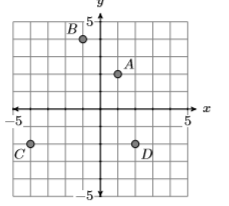
Відповідь

Домен$=\{-4,-1,1,2\}$ і діапазон$=\{-2,2,4\}$

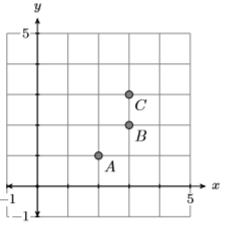
10)

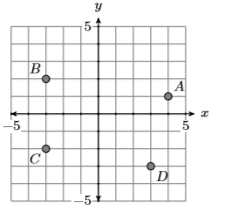
У вправах 11-18 визначте, чи є дане відношення функцією.

11)$R=\{(-6,-4),(-4,-4),(1,-4)\}$

Відповідь

Функція

12)$T=\{(-8,-3),(-4,-3),(2,-3)\}$

13)$T=\{(-1,-7),(2,-5),(4,-2)\}$

Відповідь

Функція

14)$S=\{(-6,-6),(-4,0),(9,1)\}$

15)$T=\{(-9,1),(1,6),(1,8)\}$

Відповідь

Чи не є функцією

16)$S=\{(-7,0),(1,1),(1,2)\}$

17)$R=\{(-7,-8),(-7,-6),(-5,0)\}$

Відповідь

Чи не є функцією

18)$T=\{(-8,-9),(-8,-4),(-5,9)\}$

У вправах 19-22 визначте, чи є дане відношення функцією.

19)

Відповідь

Функція

20)

21)

Відповідь

Чи не є функцією

22)

23) Дано$f(x)=|6 x-9|$, оцініть$f(8)$.

Відповідь

$39$

24) Дано$f(x)=|8 x-3|$, оцініть$f(5)$.

25) Дано$f(x)=-2 x^{2}+8$, оцініть$f(3)$.

Відповідь

$-10$

26) Дано$f(x)=3 x^{2}+x+6$, оцініть$f(-3)$.

27) Дано$f(x)=-3 x^{2}+4 x+1$, оцініть$f(2)$.

Відповідь

$-3$

28) Дано$f(x)=-3 x^{2}+4 x-2$, оцініть$f(2)$.

29) Дано$f(x)=|5 x+9|$, оцініть$f(-8)$.

Відповідь

$31$

30) Дано$f(x)=|9 x-6|$, оцініть$f(4)$.

31) Дано$f(x)=\sqrt{x-6}$, оцініть$f(42)$.

Відповідь

$6$

32) Дано$f(x)=\sqrt{x+8}$, оцініть$f(41)$.

33) Дано$f(x)=\sqrt{x-7}$, оцініть$f(88)$.

Відповідь

$9$

34) Дано$f(x)=\sqrt{x+9}$, оцініть$f(16)$.

35) Дано$f(x)=-4 x+6$, оцініть$f(8)$.

Відповідь

$-26$

36) Дано$f(x)=-9 x+2$, оцініть$f(-6)$.

37) Дано$f(x)=-6 x+7$, оцініть$f(8)$.

Відповідь

$-41$

38) Дано$f(x)=-6 x-2$, оцініть$f(5)$.

39) Дано$f(x)=-2 x^{2}+3 x+2$ і$g(x)=3 x^{2}+5 x-5$, оцінити$f(3)$ і$g(3)$.

Відповідь

$f(3)=-7$і$g(3)=37$

40) Дано$f(x)=3 x^{2}-3 x-5$ і$g(x)=2 x^{2}-5 x-8$, оцінити$f(-2)$ і$g(-2)$.

41) Дано$f(x)=6 x-2$ і$g(x)=-8 x+9$, оцінити$f(-7)$ і$g(-7)$.

Відповідь

$f(-7)=-44$і$g(-7)=65$

42) Дано$f(x)=5 x-3$ і$g(x)=9 x-9$, оцінити$f(-2)$ і$g(-2)$.

43) Дано$f(x)=4 x-3$ і$g(x)=-3 x+8$, оцінити$f(-3)$ і$g(-3)$.

Відповідь

$f(-3)=-15$і$g(-3)=17$

44) Дано$f(x)=8 x+7$ і$g(x)=2 x-7$, оцінити$f(-9)$ і$g(-9)$.

45) Дано$f(x)=-2 x^{2}+5 x-9$ і$g(x)=-2 x^{2}+3 x-4$, оцінити$f(-2)$ і$g(-2)$.

Відповідь

$f(-2)=-27$і$g(-2)=-18$

46) Дано$f(x)=-3 x^{2}+5 x-2$ і$g(x)=3 x^{2}-4 x+2$, оцінити$f(-1)$ і$g(-1)$.

5.2: Поліноми

У вправах 1-6 вкажіть коефіцієнт і ступінь кожного з наступних термінів.

1)$3 v^{5} u^{6}$

Відповідь

$=3,$Ступінь коефіцієнта$=11$

2)$-3 b^{5} z^{8}$

3)$-5 v^{6}$

Відповідь

$=-5,$Ступінь коефіцієнта$=6$

4)$-5 c^{3}$

5)$2 u^{7} x^{4} d^{5}$

Відповідь

$=2,$Ступінь коефіцієнта$=16$

6)$9 w^{4} c^{5} u^{7}$

У вправах 7-16 вкажіть, чи є кожне з наступних виразів мономіальним, біноміальним або триноміальним.

7)$-7 b^{9} c^{3}$

Відповідь

Мономіальний

8)$7 b^{6} c^{2}$

9)$4 u+7 v$

Відповідь

Біноміальний

10)$-3 b+5 c$

11)$3 b^{4}-9 b c+9 c^{2}$

Відповідь

Тримінал

12)$8 u^{4}+5 u v+3 v^{4}$

13)$5 s^{2}+9 t^{7}$

Відповідь

Біноміальний

14)$-8 x^{6}-6 y^{7}$

15)$2 u^{3}-5 u v-4 v^{4}$

Відповідь

Тримінал

16)$6 y^{3}-4 y z+7 z^{3}$

У Вправах 17-20 сортуйте кожен із заданих поліномів у спадних ступенях$x$.

17)$-2 x^{7}-9 x^{13}-6 x^{12}-7 x^{17}$

Відповідь

$-7 x^{17}-9 x^{13}-6 x^{12}-2 x^{7}$

18)$2 x^{4}-8 x^{19}+3 x^{10}-4 x^{2}$

19)$8 x^{6}+2 x^{15}-3 x^{11}-2 x^{2}$

Відповідь

$2 x^{15}-3 x^{11}+8 x^{6}-2 x^{2}$

20)$2 x^{6}-6 x^{7}-7 x^{15}-9 x^{18}$

У вправах 21-24 сортуйте кожен із заданих поліномів у висхідних ступенях$x$.

21)$7 x^{17}+3 x^{4}-2 x^{12}+8 x^{14}$

Відповідь

$3 x^{4}-2 x^{12}+8 x^{14}+7 x^{17}$

22)$6 x^{18}-6 x^{4}-2 x^{19}-7 x^{14}$

23)$2 x^{13}+3 x^{18}+8 x^{7}+5 x^{4}$

Відповідь

$5 x^{4}+8 x^{7}+2 x^{13}+3 x^{18}$

24)$-6 x^{18}-8 x^{11}-9 x^{15}+5 x^{12}$

У вправах 25-32, спростити даний многочлен, комбінуючи подібні терміни, а потім розставляючи свою відповідь у спадних степенях$x$.

25)$-5 x+3-6 x^{3}+5 x^{2}-9 x+3-3 x^{2}+6 x^{3}$

Відповідь

$2 x^{2}-14 x+6$

26)$-2 x^{3}+8 x-x^{2}+5+7+6 x^{2}+4 x^{3}-9 x$

27)$4 x^{3}+6 x^{2}-8 x+1+8 x^{3}-7 x^{2}+5 x-8$

Відповідь

$12 x^{3}-x^{2}-3 x-7$

28)$-8 x^{3}-2 x^{2}-7 x-3+7 x^{3}-9 x^{2}-8 x+9$

29)$x^{2}+9 x-3+7 x^{2}-3 x-8$

Відповідь

$8 x^{2}+6 x-11$

30)$-4 x^{2}-6 x+3-3 x^{2}+3 x-6$

31)$8 x+7+2 x^{2}-8 x-3 x^{3}-x^{2}$

Відповідь

$-3 x^{3}+x^{2}+7$

32)$-x^{2}+8-7 x+8 x-5 x^{2}+4 x^{3}$

У вправах 33-44 спростіть даний многочлен, комбінуючи подібні терміни, потім розташувавши свою відповідь в розумному порядку, можливо, в спадних ступенях будь-якої змінної. Примітка. Відповіді можуть відрізнятися залежно від того, яку змінну ви виберете для диктування порядку.

33)$-8 x^{2}-4 x z-2 z^{2}-3 x^{2}-8 x z+2 z^{2}$

Відповідь

$-11 x^{2}-12 x z$

34)$-5 x^{2}+9 x z-4 z^{2}-6 x^{2}-7 x z+7 z^{2}$

35)$-6 u^{3}+4 u v^{2}-2 v^{3}-u^{3}+6 u^{2} v-5 u v^{2}$

Відповідь

$-7 u^{3}+6 u^{2} v-u v^{2}-2 v^{3}$

36)$7 a^{3}+6 a^{2} b-5 a b^{2}+4 a^{3}+6 a^{2} b+6 b^{3}$

37)$-4 b^{2} c-3 b c^{2}-5 c^{3}+9 b^{3}-3 b^{2} c+5 b c^{2}$

Відповідь

$9 b^{3}-7 b^{2} c+2 b c^{2}-5 c^{3}$

38)$4 b^{3}-6 b^{2} c+9 b c^{2}-9 b^{3}-8 b c^{2}+3 c^{3}$

39)$-8 y^{2}+6 y z-7 z^{2}-2 y^{2}-3 y z-9 z^{2}$

Відповідь

$-10 y^{2}+3 y z-16 z^{2}$

40)$8 x^{2}+x y+3 y^{2}-x^{2}+7 x y+y^{2}$

41)$7 b^{2} c+8 b c^{2}-6 c^{3}-4 b^{3}+9 b c^{2}-6 c^{3}$

Відповідь

$-4 b^{3}+7 b^{2} c+17 b c^{2}-12 c^{3}$

42)$7 x^{3}-9 x^{2} y+3 y^{3}+7 x^{3}+3 x y^{2}-7 y^{3}$

43)$9 a^{2}+a c-9 c^{2}-5 a^{2}-2 a c+2 c^{2}$

Відповідь

$4 a^{2}-a c-7 c^{2}$

44)$7 u^{2}+3 u v-6 v^{2}-6 u^{2}+7 u v+6 v^{2}$

У вправах 45-50 викласти ступінь даного полінома.

45)$3 x^{15}+4+8 x^{3}-8 x^{19}$

Відповідь

$19$

46)$-4 x^{6}-7 x^{16}-5+3 x^{18}$

47)$7 x^{10}-3 x^{18}+9 x^{4}-6$

Відповідь

$18$

48)$3 x^{16}-8 x^{5}+x^{8}+7$

49)$-2-x^{7}-5 x^{5}+x^{10}$

Відповідь

$10$

50)$x^{11}+7 x^{16}+8-7 x^{10}$

51) Дано$f(x)=5 x^{3}+4 x^{2}-6$, оцініть$f(-1)$.

Відповідь

$-7$

52) Дано$f(x)=-3 x^{3}+3 x^{2}-9$, оцініть$f(-1)$.

53) Дано$f(x)=5 x^{4}-4 x-6$, оцініть$f(-2)$.

Відповідь

$82$

54) Дано$f(x)=-2 x^{4}-4 x-9$, оцініть$f(2)$.

55) Дано$f(x)=3 x^{4}+5 x^{3}-9$, оцініть$f(-2)$.

Відповідь

$-1$

56) Дано$f(x)=-3 x^{4}+2 x^{3}-6$, оцініть$f(-1)$.

57) Дано$f(x)=3 x^{4}-5 x^{2}+8$, оцініть$f(-1)$.

Відповідь

$6$

58) Дано$f(x)=-4 x^{4}-5 x^{2}-3$, оцініть$f(3)$.

59) Дано$f(x)=-2 x^{3}+4 x-9$, оцініть$f(2)$.

Відповідь

$-17$

60) Дано$f(x)=4 x^{3}+3 x+7$, оцініть$f(-2)$.

У Вправи 61-64 використовуйте графічний калькулятор, щоб намалювати заданий квадратичний многочлен. У кожному випадку графік є параболою, тому відрегулюйте параметри WINDOW, доки вершина не буде видима у вікні перегляду, а потім дотримуйтесь Правил подання калькулятора, коли повідомляєте про ваше рішення про домашнє завдання.

61)$p(x)=-2 x^{2}+8 x+32$

Відповідь

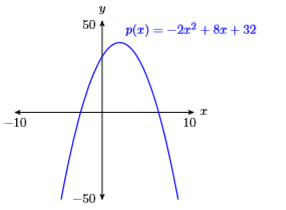
62)$p(x)=2 x^{2}+6 x-18$

63)$p(x)=3 x^{2}-8 x-35$

Відповідь

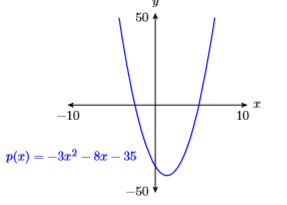
64)$p(x)=-4 x^{2}-9 x+50$

У Вправи 65-68 використовуйте графічний калькулятор для ескізу полінома, використовуючи задані параметри WINDOW. Дотримуйтесь вказівок щодо подання калькулятора, коли повідомляєте про своє рішення на домашнє завдання.

65)$p(x)=x^{3}-4 x^{2}-11 x+30$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

Відповідь

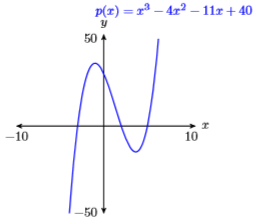
66)$p(x)=-x^{3}+4 x^{2}+27 x-90$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-150 \quad \mathbf{Y} \max =50$

67)$p(x)=x^{4}-10 x^{3}-4 x^{2}+250 x-525$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-1000 \quad \mathbf{Y} \max =500$

Відповідь

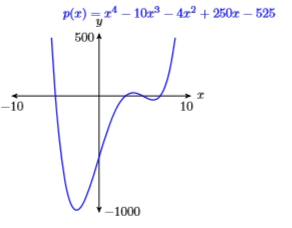
68)$p(x)=-x^{4}+2 x^{3}+35 x^{2}-36 x-180$
$\mathbf{X} \min =-10 \quad \mathbf{X} \max =10$
$\mathbf{Y} \min =-50 \quad \mathbf{Y} \max =50$

5.3: Застосування поліномів

1) Фірма збирає дані про суму, яку вона витрачає на рекламу, і отриманий компанією дохід. Обидва фрагменти даних знаходяться в тисячах доларів.

$x$(витрати на рекламу)	0	5	15	20	25	30
$R$(дохід)	6347	6524	7591	8251	7623	7478

Потім дані складаються з наступним поліномом другого ступеня, де$x$ сума вкладена в тисячі доларів і$R(x)$ сума доходу, отриманого фірмою (також у тисячах доларів).

$R(x)=−4.1x^2 + 166.8x+ 6196$

Використовуйте графік, а потім поліном, щоб оцінити дохід фірми, коли фірма інвестувала$\$10,000$ в рекламу.

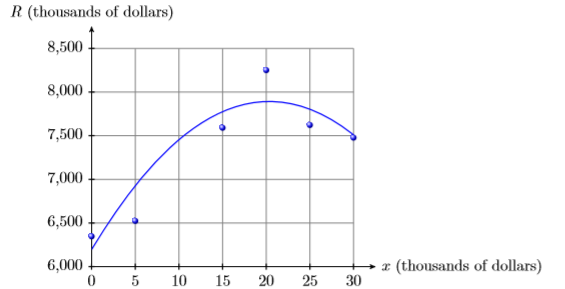
Відповідь

Приблизно$\$7,454,000$

2) У таблиці нижче наведено приблизну кількість випадків СНІД у Сполучених Штатах за роки 1999-2003.

Рік	1999	2000	2002	2003
Випадки СНІДу	41 356	41 267	41 289	43 171

Потім дані будуються з наступним поліномом другого ступеня, де$t$ - кількість років, що минули з 1998 року, і$N(t)$ кількість випадків допомоги, зареєстрованих через$t$ роки після 1998 року.

$N(t) = 345.14t^2−1705.7t+ 42904$

Використовуйте графік, а потім поліном, щоб оцінити кількість випадків СНІДу в 2001 році.

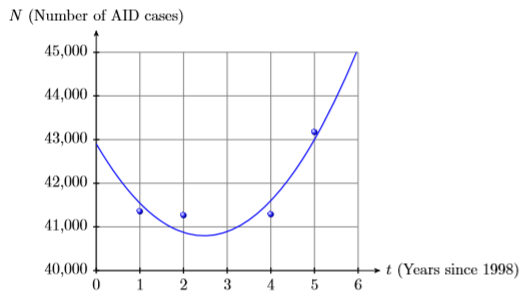
3) Наступна таблиця фіксує концентрацію (в міліграмах на літр) медикаменту в крові пацієнта після закінчення вказаних часів.

Час (Години)	0	0.5	1	0.5	2.5
Концентрація (мг/л)	0	78.1	99.8	84.4	15,6

Потім дані наносяться наступним поліномом другого ступеня, де$t$ - кількість годин, що минули з моменту прийому ліків, і$C(t)$ концентрація (в міліграмах на літр) препарату в крові пацієнта після того, як пройшли$t$ години.

$C(t)=−56.214t^2 + 139.31t+9.35$

Використовуйте графік, а потім поліном, щоб оцінити концентрацію ліків у крові пацієнта через$2$ години після прийому ліків.

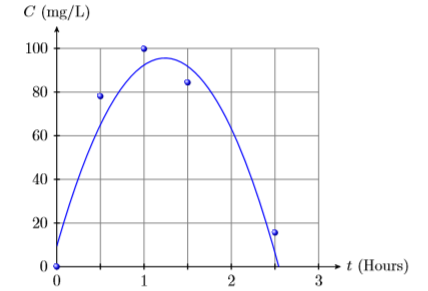
Відповідь

Приблизно$63 \mathrm{mg} / \mathrm{L}$

4) Наступна таблиця фіксує населення (в мільйоні людей) Сполучених Штатів за даний рік.

Рік	1900	1920	1940	1960	1980	2000	2010
Населення (мільйони)	76.2	106.0	132.2	179.3	26.5	281.4	307.7

Потім дані наносяться наступним поліномом другого ступеня, де$t$ - кількість років, що минули з 1990 року, і$P(t)$ населення (у мільйоні)$t$ років після 1990 року.

$P(t)=0 .008597t^2 +1,1738t+ 76 .41$

Використовуйте графік, а потім поліном, щоб оцінити чисельність населення США в 1970 році.

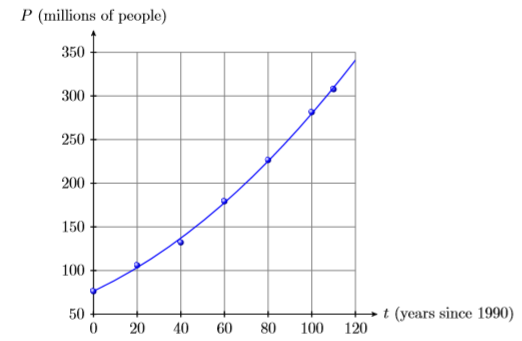
5) Якщо снаряд запущений з початковою швидкістю$457$ метрів в секунду ($457 \mathrm{m/s}$) від$75$ метрів на даху ($75 \mathrm{m}$) над рівнем землі, то в який час снаряд першим досягне висоти$6592$ метрів ($6592 \mathrm{m}$)? Округлите відповідь до найближчої секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Відповідь

$17.6$секунд

6) Якщо снаряд запущений з початковою швидкістю$236$ метрів в секунду ($236 \mathrm{m/s}$) від$15$ метрів на даху ($15\mathrm{m}$) над рівнем землі, то в який час снаряд першим досягне висоти$1838$ метрів ($1838\mathrm{m}$)? Округлите відповідь до найближчої секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

7) Якщо снаряд запущений з початковою швидкістю$229$ метрів в секунду ($229 \mathrm{m/s}$) від$58$ метрів на даху ($58\mathrm{m}$) над рівнем землі, то в який час снаряд першим досягне висоти$1374$ метрів ($1374\mathrm{m}$)? Округлите відповідь до найближчої секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить 9,8 метра в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Відповідь

$6.7$секунд

8) Якщо снаряд запущений з початковою швидкістю$234$ метрів в секунду ($234 \mathrm{m/s}$) від$16$ метрів на даху ($16\mathrm{m}$) над рівнем землі, то в який час снаряд першим досягне висоти$1882$ метрів ($1882\mathrm{m}$)? Округлите відповідь до найближчої секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

У вправах 9-12 спочатку використовуйте алгебраїчну техніку, щоб знайти нуль даної функції, а потім скористайтеся утилітою 2: нуль на графічному калькуляторі, щоб знайти нуль функції. Використовуйте Рекомендації щодо подання калькулятора, коли повідомляєте про нуль, знайдений за допомогою графічного калькулятора.

9)$f(x)=3.25 x-4.875$

Відповідь

Нуль:$1.5$

10)$f(x)=3.125-2.5 x$

11)$f(x)=3.9-1.5 x$

Відповідь

Нуль:$2.6$

12)$f(x)=0.75 x+2.4$

13) Якщо снаряд запущений з початковою швидкістю$203$ метрів в секунду ($203 \mathrm{m/s}$) з$52$ метрів на даху ($52\mathrm{m}$) над рівнем землі, то в який час снаряд повернеться на рівень землі? Округлите відповідь до найближчої десятої частки секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Відповідь

$41.7$секунд

14) Якщо снаряд запущений з початковою швидкістю$484$ метрів в секунду ($484 \mathrm{m/s}$) з$17$ метрів на даху ($17\mathrm{m}$) над рівнем землі, то в який час снаряд повернеться на рівень землі? Округлите відповідь до найближчої десятої частки секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

15) Якщо снаряд запущений з початковою швидкістю$276$ метрів в секунду ($276 \mathrm{m/s}$) з$52$ метрів на даху ($52\mathrm{m}$) над рівнем землі, то в який час снаряд повернеться на рівень землі? Округлите відповідь до найближчої десятої частки секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

Відповідь

$56.5$секунд

16) Якщо снаряд запущений з початковою швидкістю$204$ метрів в секунду ($204 \mathrm{m/s}$) з$92$ метрів на даху ($92\mathrm{m}$) над рівнем землі, то в який час снаряд повернеться на рівень землі? Округлите відповідь до найближчої десятої частки секунди.

Примітка: Прискорення за рахунок сили тяжіння поблизу земної поверхні становить$9.8$ метри в секунду в секунду ($9.8 \mathrm{m} / \mathrm{s}^{2}$).

5.4: Додавання та віднімання многочленів

У вправах 1-8 спростіть даний вираз. Влаштуйте свою відповідь в якомусь розумному порядку.

1)$\left(-8 r^{2} t+7 r t^{2}+3 t^{3}\right)+\left(9 r^{3}+2 r t^{2}+4 t^{3}\right)$

Відповідь

$9 r^{3}-8 r^{2} t+9 r t^{2}+7 t^{3}$

2)$\left(-a^{3}-8 a c^{2}-7 c^{3}\right)+\left(-7 a^{3}-8 a^{2} c+8 a c^{2}\right)$

3)$\left(7 x^{2}-6 x-9\right)+\left(8 x^{2}+10 x+9\right)$

Відповідь

$15 x^{2}+4 x$

4)$\left(-7 x^{2}+5 x-6\right)+\left(-10 x^{2}-1\right)$

5)$\left(-2 r^{2}+7 r s+4 s^{2}\right)+\left(-9 r^{2}+7 r s-2 s^{2}\right)$

Відповідь

$-11 r^{2}+14 r s+2 s^{2}$

6)$\left(-2 r^{2}+3 r t-4 t^{2}\right)+\left(7 r^{2}+4 r t-7 t^{2}\right)$

7)$\left(-8 y^{3}-3 y^{2} z-6 z^{3}\right)+\left(-3 y^{3}+7 y^{2} z-9 y z^{2}\right)$

Відповідь

$-11 y^{3}+4 y^{2} z-9 y z^{2}-6 z^{3}$

8)$\left(7 y^{2} z+8 y z^{2}+2 z^{3}\right)+\left(8 y^{3}-8 y^{2} z+9 y z^{2}\right)$

У вправах 9-14 спростіть даний вираз, розподіляючи знак мінус.

9)$-\left(5 x^{2}-4\right)$

Відповідь

$-5 x^{2}+4$

10)$-\left(-8 x^{2}-5\right)$

11)$-\left(9 r^{3}-4 r^{2} t-3 r t^{2}+4 t^{3}\right)$

Відповідь

$-9 r^{3}+4 r^{2} t+3 r t^{2}-4 t^{3}$

12)$-\left(7 u^{3}-8 u^{2} v+6 u v^{2}+5 v^{3}\right)$

13)$-\left(-5 x^{2}+9 x y+6 y^{2}\right)$

Відповідь

$5 x^{2}-9 x y-6 y^{2}$

14)$-\left(-4 u^{2}-6 u v+5 v^{2}\right)$

У вправах 15-22 спростіть даний вираз. Влаштуйте свою відповідь в якомусь розумному порядку.

15)$\left(-u^{3}-4 u^{2} w+7 w^{3}\right)-\left(u^{2} w+u w^{2}+3 w^{3}\right)$

Відповідь

$-u^{3}-5 u^{2} w-u w^{2}+4 w^{3}$

16)$\left(-b^{2} c+8 b c^{2}+8 c^{3}\right)-\left(6 b^{3}+b^{2} c-4 b c^{2}\right)$

17)$\left(2 y^{3}-2 y^{2} z+3 z^{3}\right)-\left(-8 y^{3}+5 y z^{2}-3 z^{3}\right)$

Відповідь

$10 y^{3}-2 y^{2} z-5 y z^{2}+6 z^{3}$

18)$\left(4 a^{3}+6 a c^{2}+5 c^{3}\right)-\left(2 a^{3}+8 a^{2} c-7 a c^{2}\right)$

19)$\left(-7 r^{2}-9 r s-2 s^{2}\right)-\left(-8 r^{2}-7 r s+9 s^{2}\right)$

Відповідь

$r^{2}-2 r s-11 s^{2}$

20)$\left(-4 a^{2}+5 a b-2 b^{2}\right)-\left(-8 a^{2}+7 a b+2 b^{2}\right)$

21)$\left(10 x^{2}+2 x-6\right)-\left(-8 x^{2}+14 x+17\right)$

Відповідь

$18 x^{2}-12 x-23$

22)$\left(-5 x^{2}+19 x-5\right)-\left(-15 x^{2}+19 x+8\right)$

У вправах 23-28, для заданих поліноміальних функцій$f(x)$ і$g(x)$, спростити$f(x)+g(x)$. Організуйте свою відповідь у спадних повноваженнях$x$.

23)$\begin{aligned}f(x)&=-2 x^{2}+9 x+7 \\ g(x)&=8 x^{3}-7 x^{2}+5\end{aligned}$

Відповідь

$8 x^{3}-9 x^{2}+9 x+12$

24)$\begin{aligned}f(x)&=-8 x^{3}+6 x-9 \\ g(x)&=x^{3}-x^{2}+3 x\end{aligned}$

25)$\begin{aligned}f(x)&=5 x^{3}-5 x^{2}+8 x \\ g(x)&=7 x^{2}-2 x-9\end{aligned}$

Відповідь

$5 x^{3}+2 x^{2}+6 x-9$

26)$\begin{aligned}f(x)&=-x^{2}+8 x+1 \\ g(x)&=-7 x^{3}+8 x-9\end{aligned}$

27)$\begin{aligned}f(x)&=-3 x^{2}-8 x-9 \\ g(x)&=5 x^{2}-4 x+4\end{aligned}$

Відповідь

$2 x^{2}-12 x-5$

28)$\begin{aligned}f(x)&=-3 x^{2}+x-8 \\ g(x)&=7 x^{2}-9\end{aligned}$

У вправах 29-34, для заданих поліноміальних функцій$f(x)$ і$g(x)$, спростити$f(x)−g(x)$. Організуйте свою відповідь у спадних повноваженнях$x$.

29)$\begin{aligned}f(x)&=-6 x^{3}-7 x+7 \\ g(x)&=-3 x^{3}-3 x^{2}-8 x\end{aligned}$

Відповідь

$-3 x^{3}+3 x^{2}+x+7$

30)$\begin{aligned}f(x)&=5 x^{3}-5 x+4 \\ g(x)&=-8 x^{3}-2 x^{2}-3 x\end{aligned}$

31)$\begin{aligned}f(x)&=12 x^{2}-5 x+4 \\ g(x)&=8 x^{2}-16 x-7\end{aligned}$

Відповідь

$4 x^{2}+11 x+11$

32)$\begin{aligned}f(x)&=-7 x^{2}+12 x+17 \\ g(x)&=-10 x^{2}-17\end{aligned}$

33)$\begin{aligned}f(x)&=-3 x^{3}-4 x+2 \\ g(x)&=-4 x^{3}-7 x^{2}+6\end{aligned}$

Відповідь

$x^{3}+7 x^{2}-4 x-4$

34)$\begin{aligned}f(x)&=-9 x^{2}+9 x+3 \\ g(x)&=7 x^{3}+7 x^{2}+5\end{aligned}$

У Вправах 35-36 знайдіть площу даного квадрата, підсумовуючи площі чотирьох його частин.

35)

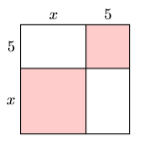
Відповідь

$x^{2}+10 x+25$

36)

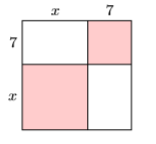
37) Рейчел веде малий бізнес з продажу плетених кошиків. Її ділові витрати на виробництво і продаж х плетених кошиків задаються поліноміальною функцією$C(x) = 232+ 7x−0.0085x^2$. Дохід, який вона отримує від продажу х плетених кошиків, дається поліноміальною функцією$R(x) = 33.45x$. Знайдіть формулу для того$P(x)$, щоб прибуток отримувався від продажу$x$ плетених кошиків. Використовуйте свою формулу, щоб визначити прибуток Рейчел, якщо вона продає$233$ плетені кошики. Округлите відповідь до найближчого цента.

Відповідь

$\$6,392.31$

38) Елоїза веде невеликий бізнес з продажу дитячих ліжечок. Її ділові витрати на виробництво та продаж$x$ дитячих ліжечок задаються поліноміальною функцією$C(x) = 122 + 8x − 0.0055x^2$. Дохід, який вона отримує від продажу$x$ дитячих ліжечок, дається поліноміальною функцією$R(x) = 33.45x$. Знайдіть формулу для того$P(x)$, щоб прибуток отримувався від продажу$x$ дитячих ліжечок. Використовуйте свою формулу, щоб визначити прибуток Елоїзи, якщо вона продає$182$ дитячі ліжечка. Округлите відповідь до найближчого цента.

5.5: Закони експонентів

У вправах 1-8 спростіть кожне з заданих експоненціальних виразів.

1)$(-4)^{3}$

Відповідь

$-64$

2)$(-9)^{2}$

3)$\left(-\dfrac{5}{7}\right)^{0}$

Відповідь

$1$

4)$\left(-\dfrac{2}{5}\right)^{0}$

5)$\left(-\dfrac{4}{3}\right)^{2}$

Відповідь

$\dfrac{16}{9}$

6)$\left(-\dfrac{2}{3}\right)^{2}$

7)$(-19)^{0}$

Відповідь

$1$

8)$(-17)^{0}$

У вправах 9-18 спростити кожне з заданих експоненціальних виразів.

9)$(7 v-6 w)^{18} \cdot(7 v-6 w)^{17}$

Відповідь

$(7 v-6 w)^{35}$

10)$(8 a+7 c)^{3} \cdot(8 a+7 c)^{19}$

11)$3^{4} \cdot 3^{0}$

Відповідь

$3^{4}$

12)$5^{7} \cdot 5^{0}$

13)$4^{n} \cdot 4^{8 n+3}$

Відповідь

$4^{9 n+3}$

14)$4^{6 m+5} \cdot 4^{m-5}$

15)$x^{8} \cdot x^{3}$

Відповідь

$x^{11}$

16)$a^{9} \cdot a^{15}$

17)$2^{5} \cdot 2^{3}$

Відповідь

$2^{8}$

18)$2^{10} \cdot 2^{3}$

У вправах 19-28 спростіть кожне з заданих експоненціальних виразів.

19)$\dfrac{4^{16}}{4^{16}}$

Відповідь

$1$

20)$\dfrac{3^{12}}{3^{12}}$

21)$\dfrac{w^{11}}{w^{7}}$

Відповідь

$w^{4}$

22)$\dfrac{c^{10}}{c^{8}}$

23)$\dfrac{(9 a-8 c)^{15}}{(9 a-8 c)^{8}}$

Відповідь

$(9 a-8 c)^{7}$

24)$\dfrac{(4 b+7 c)^{15}}{(4 b+7 c)^{5}}$

25)$\dfrac{2^{9 n+5}}{2^{3 n-4}}$

Відповідь

$2^{6 n+9}$

26)$\dfrac{2^{4 k-9}}{2^{3 k-8}}$

27)$\dfrac{4^{17}}{4^{9}}$

Відповідь

$4^{8}$

28)$\dfrac{2^{17}}{2^{6}}$

У вправах 29-38 спростити кожне з заданих експоненціальних виразів.

29)$\left(4^{8 m-6}\right)^{7}$

Відповідь

$4^{56 m-42}$

30)$\left(2^{2 m-9}\right)^{3}$

31)$\left[(9 x+5 y)^{3}\right]^{7}$

Відповідь

$(9 x+5 y)^{21}$

32)$\left[(4 u-v)^{8}\right]^{9}$

33)$\left(4^{3}\right)^{2}$

Відповідь

$4^{6}$

34)$\left(3^{4}\right)^{2}$

35)$\left(c^{4}\right)^{7}$

Відповідь

$c^{28}$

36)$\left(w^{9}\right)^{5}$

37)$\left(6^{2}\right)^{0}$

Відповідь

$1$

38)$\left(8^{9}\right)^{0}$

У вправах 39-48 спростити кожне з заданих експоненціальних виразів.

39)$(u w)^{5}$

Відповідь

$u^{5} w^{5}$

40)$(a c)^{4}$

41)$(-2 y)^{3}$

Відповідь

$-8 y^{3}$

42)$(-2 b)^{3}$

43)$\left(3 w^{9}\right)^{4}$

Відповідь

$81 w^{36}$

44)$\left(-3 u^{9}\right)^{4}$

45)$\left(-3 x^{8} y^{2}\right)^{4}$

Відповідь

$81 x^{32} y^{8}$

46)$\left(2 x^{8} z^{6}\right)^{4}$

47)$\left(7 s^{6 n}\right)^{3}$

Відповідь

$343 s^{18 n}$

48)$\left(9 b^{6 n}\right)^{3}$

У вправах 49-56 спростити кожне з заданих експоненціальних виразів.

49)$\left(\dfrac{v}{2}\right)^{3}$

Відповідь

$\dfrac{v^{3}}{8}$

50)$\left(\dfrac{t}{9}\right)^{2}$

51)$\left(-\dfrac{2}{u}\right)^{2}$

Відповідь

$\dfrac{4}{u^{2}}$

52)$\left(-\dfrac{3}{w}\right)^{3}$

53)$\left(-\dfrac{r^{8}}{5}\right)^{4}$

Відповідь

$\dfrac{r^{32}}{625}$

54)$\left(-\dfrac{x^{11}}{5}\right)^{5}$

55)$\left(\dfrac{5}{c^{9}}\right)^{4}$

Відповідь

$\dfrac{625}{c^{36}}$

56)$\left(\dfrac{5}{u^{12}}\right)^{2}$

57) Заповніть кожен із законів показників, представлених у першій колонці, а потім використовуйте результати для спрощення виразів у другому стовпці.

$a^{m} a^{n}=?$	$a^{3} a^{5}=?$
$\dfrac{a^{m}}{a^{n}}=?$	$\dfrac{a^{6}}{a^{2}}=?$
$\left(a^{m}\right)^{n}=?$	$\left(a^{5}\right)^{7}=?$
$(a b)^{m}=?$	$(a b)^{9}=?$
$\left(\dfrac{a}{b}\right)^{m}=?$	$\left(\dfrac{a}{b}\right)^{3}=?$

Відповідь

Загальні відповіді:$a^{m+n}, a^{m-n}, a^{m n}, a^{m} b^{m}, \dfrac{a^m}{b^m}$.

Конкретні відповіді:$a^{8}, a^{4}, a^{35}, a^{9} b^{9}, \dfrac{a^3}{b^3}$.

5.6: Множення многочленів

У вправах 1-10 спростіть даний вираз.

1)$-3(7 r)$

Відповідь

$-21 r$

2)$7(3 a)$

3)$\left(-9 b^{3}\right)\left(-8 b^{6}\right)$

Відповідь

$72b^{9}$

4)$\left(8 s^{3}\right)\left(-7 s^{4}\right)$

5)$\left(-7 r^{2} t^{4}\right)\left(7 r^{5} t^{2}\right)$

Відповідь

$-49 r^{7} t^{6}$

6)$\left(-10 s^{2} t^{8}\right)\left(-7 s^{4} t^{3}\right)$

7)$\left(-5 b^{2} c^{9}\right)\left(-8 b^{4} c^{4}\right)$

Відповідь

$40 b^{6} c^{13}$

8)$\left(-9 s^{2} t^{8}\right)\left(7 s^{5} t^{4}\right)$

9)$\left(-8 v^{3}\right)\left(4 v^{4}\right)$

Відповідь

$-32 v^{7}$

10)$\left(-9 y^{3}\right)\left(3 y^{5}\right)$

У вправах 11-22 використовуйте розподільну властивість, щоб розширити заданий вираз.

11)$9\left(-2 b^{2}+2 b+9\right)$

Відповідь

$-18 b^{2}+18 b+81$

12)$9\left(-4 b^{2}+7 b-8\right)$

13)$-4\left(10 t^{2}-7 t-6\right)$

Відповідь

$-40 t^{2}+28 t+24$

14)$-5\left(-7 u^{2}-7 u+2\right)$

15)$-8 u^{2}\left(-7 u^{3}-8 u^{2}-2 u+10\right)$

Відповідь

$56 u^{5}+64 u^{4}+16 u^{3}-80 u^{2}$

16)$-3 s^{2}\left(-7 s^{3}-9 s^{2}+6 s+3\right)$

17)$10 s^{2}\left(-10 s^{3}+2 s^{2}+2 s+8\right)$

Відповідь

$-100 s^{5}+20 s^{4}+20 s^{3}+80 s^{2}$

18)$8 u^{2}\left(9 u^{3}-5 u^{2}-2 u+5\right)$

19)$2 s t\left(-4 s^{2}+8 s t-10 t^{2}\right)$

Відповідь

$-8 s^{3} t+16 s^{2} t^{2}-20 s t^{3}$

20)$7 u v\left(-9 u^{2}-3 u v+4 v^{2}\right)$

21)$-2 u w\left(10 u^{2}-7 u w-2 w^{2}\right)$

Відповідь

$-20 u^{3} w+14 u^{2} w^{2}+4 u w^{3}$

22)$-6 v w\left(-5 v^{2}+9 v w+5 w^{2}\right)$

У вправах 23-30 використовуйте техніку, продемонстровану в прикладі 5.6.8 та прикладі 5.6.9, щоб розширити кожне з наступних виразів за допомогою властивості розподілу.

23)$(-9 x-4)(-3 x+2)$

Відповідь

$27 x^{2}-6 x-8$

24)$(4 x-10)(-2 x-6)$

25)$(3 x+8)(3 x-2)$

Відповідь

$9 x^{2}+18 x-16$

26)$(-6 x+8)(-x+1)$

27)$-12 x^{3}+14 x^{2}+6 x-5$

Відповідь

$-\dfrac{930}{289}$

28)$(4 x-6)\left(-7 x^{2}-10 x+10\right)$

29)$(x-6)\left(-2 x^{2}-4 x-4\right)$

Відповідь

$-2 x^{3}+8 x^{2}+20 x+24$

30)$(5 x-10)\left(-3 x^{2}+7 x-8\right)$

У вправах 31-50 використовуйте техніку швидкого скорочення, продемонстровану в прикладі 5.6.10, прикладі 5.6.11 та прикладі 5.6.12, щоб розширити кожне з наступних виразів за допомогою властивості розподілу.

31)$(8 u-9 w)(8 u-9 w)$

Відповідь

$64 u^{2}-144 u w+81 w^{2}$

32)$(3 b+4 c)(-8 b+10 c)$

33)$(9 r-7 t)(3 r-9 t)$

Відповідь

$27 r^{2}-102 r t+63 t^{2}$

34)$(-6 x-3 y)(-6 x+9 y)$

35)$(4 r-10 s)\left(-10 r^{2}+10 r s-7 s^{2}\right)$

Відповідь

$-40 r^{3}+140 r^{2} s-128 r s^{2}+70 s^{3}$

36)$(5 s-9 t)\left(-3 s^{2}+4 s t-9 t^{2}\right)$

37)$(9 x-2 z)\left(4 x^{2}-4 x z-10 z^{2}\right)$

Відповідь

$36 x^{3}-44 x^{2} z-82 x z^{2}+20 z^{3}$

38)$(r-4 t)\left(7 r^{2}+4 r t-2 t^{2}\right)$

39)$(9 r+3 t)^{2}$

Відповідь

$81 r^{2}+54 r t+9 t^{2}$

40)$(4 x+8 z)^{2}$

41)$(4 y+5 z)(4 y-5 z)$

Відповідь

$16 y^{2}-25 z^{2}$

42)$(7 v+2 w)(7 v-2 w)$

43)$(7 u+8 v)(7 u-8 v)$

Відповідь

$49 u^{2}-64 v^{2}$

44)$(6 b+8 c)(6 b-8 c)$

45)$(7 b+8 c)^{2}$

Відповідь

$49 b^{2}+112 b c+64 c^{2}$

46)$(2 b+9 c)^{2}$

47)$\left(2 t^{2}+9 t+4\right)\left(2 t^{2}+9 t+4\right)$

Відповідь

$4 t^{4}+36 t^{3}+97 t^{2}+72 t+16$

48)$\left(3 a^{2}-9 a+4\right)\left(3 a^{2}-9 a+2\right)$

49)$\left(4 w^{2}+3 w+5\right)\left(3 w^{2}-6 w+8\right)$

Відповідь

$12 w^{4}-15 w^{3}+29 w^{2}-6 w+40$

50)$\left(4 s^{2}+3 s+8\right)\left(2 s^{2}+4 s-9\right)$

51) Попит на віджети задається функцією$x = 320−0.95p$, де$x$ - попит і$p$ ціна одиниці. Яку ціну одиниці повинен стягувати рітейлер за віджети, щоб його дохід від продажів дорівнював$\$7,804$? Округліть свої відповіді до найближчого цента.

Відповідь

$\$ 26.47$,$\$ 310.37$

52) Попит на віджети задається функцією$x = 289−0.91p$, де$x$ - попит і$p$ ціна одиниці. Яку ціну одиниці повинен стягувати рітейлер за віджети, щоб його дохід від продажів дорівнював$\$7,257$? Округліть свої відповіді до найближчого цента.

53) На наступному зображенні край зовнішнього квадрата на$6$ дюйми довший, ніж в$3$ рази більше краю внутрішнього квадрата.

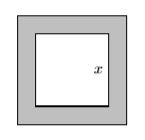
1. Висловіть площу затіненої області у вигляді многочлена з точки зору$x$, краю внутрішнього квадрата. Ваша остаточна відповідь повинна бути представлена у вигляді полінома другого ступеня у формі$A(x)=ax^2 + bx + c$.
2. З огляду на, що край внутрішнього квадрата дорівнює$5$ дюймам, використовуйте многочлен в частині (а) для визначення площі затіненої області.

Відповідь

$A(x)=8 x^{2}+36 x+36$,$A(5)=416$ квадратні дюйми

54) На наступному зображенні край зовнішнього квадрата на$3$ дюйми довший, ніж в$2$ рази більше краю внутрішнього квадрата.

1. Висловіть площу затіненої області у вигляді многочлена з точки зору$x$, краю внутрішнього квадрата. Ваша остаточна відповідь повинна бути представлена у вигляді полінома другого ступеня у формі$A(x)=ax^2 + bx + c$.
2. З огляду на, що край внутрішнього квадрата дорівнює$4$ дюймам, використовуйте многочлен в частині (а) для визначення площі затіненої області.

55) Прямокутний сад оточений рівномірною межею газонних вимірювальних$x$ одиниць шириною. Вся прямокутна ділянка$31$ вимірюється$29$ ногами.

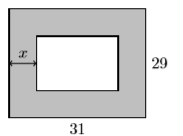
1. Знайдіть площу внутрішнього прямокутного саду у вигляді многочлена в терміні$x$. Ваша остаточна відповідь повинна бути представлена у вигляді полінома другого ступеня у формі$A(x)=ax^2 + bx + c$.
2. З огляду на, що ширина кордону дорівнює$9.3$ футам, використовуйте многочлен в частині (а) для визначення площі внутрішнього прямокутного саду.

Відповідь

$899-120 x+4 x^{2}$,$128.96$ квадратні фути

56) Прямокутний сад оточений рівномірною межею газонних вимірювальних$x$ одиниць шириною. Вся прямокутна ділянка$35$ вимірюється$24$ ногами.

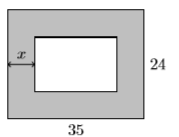
1. Знайдіть площу внутрішнього прямокутного саду у вигляді многочлена в терміні$x$. Ваша остаточна відповідь повинна бути представлена у вигляді полінома другого ступеня у формі$A(x)=ax^2 + bx + c$.
2. З огляду на, що ширина кордону дорівнює$1.5$ футам, використовуйте многочлен в частині (а) для визначення площі внутрішнього прямокутного саду.

5.7: Спеціальні продукти

У вправах 1-12 використовуйте ярлик FOIL, як у прикладі 5.7.3 та прикладі 5.7.4, щоб помножити задані біноми.

1)$(5 x+2)(3 x+4)$

Відповідь

$15 x^{2}+26 x+8$

2)$(5 x+2)(4 x+3)$

3)$(6 x-3)(5 x+4)$

Відповідь

$30 x^{2}+9 x-12$

4)$(6 x-2)(4 x+5)$

5)$(5 x-6)(3 x-4)$

Відповідь

$15 x^{2}-38 x+24$

6)$(6 x-4)(3 x-2)$

7)$(6 x-2)(3 x-5)$

Відповідь

$18 x^{2}-36 x+10$

8)$(2 x-3)(6 x-4)$

9)$(6 x+4)(3 x+5)$

Відповідь

$18 x^{2}+42 x+20$

10)$(3 x+2)(4 x+6)$

11)$(4 x-5)(6 x+3)$

Відповідь

$24 x^{2}-18 x-15$

12)$(3 x-5)(2 x+6)$

У вправах 13-20 використовуйте різницю квадратів ярлик, як у прикладі 5.7.5, щоб помножити задані біноми.

13)$(10 x-12)(10 x+12)$

Відповідь

$100 x^{2}-144$

14)$(10 x-11)(10 x+11)$

15)$(6 x+9)(6 x-9)$

Відповідь

$36 x^{2}-81$

16)$(9 x+2)(9 x-2)$

17)$(3 x+10)(3 x-10)$

Відповідь

$9 x^{2}-100$

18)$(12 x+12)(12 x-12)$

19)$(10 x-9)(10 x+9)$

Відповідь

$100 x^{2}-81$

20)$(4 x-6)(4 x+6)$

У Вправах 21-28 використовуйте квадрат біноміального скорочення, як у прикладі 5.7.8, щоб розширити вказаний вираз.

21)$(2 x+3)^{2}$

Відповідь

$4 x^{2}+12 x+9$

22)$(8 x+9)^{2}$

23)$(9 x-8)^{2}$

Відповідь

$81 x^{2}-144 x+64$

24)$(4 x-5)^{2}$

25)$(7 x+2)^{2}$

Відповідь

$49 x^{2}+28 x+4$

26)$(4 x+2)^{2}$

27)$(6 x-5)^{2}$

Відповідь

$36 x^{2}-60 x+25$

28)$(4 x-3)^{2}$

У Вправах 29-76 використовуйте відповідний ярлик, щоб помножити задані біноми.

29)$(11 x-2)(11 x+2)$

Відповідь

$121 x^{2}-4$

30)$(6 x-7)(6 x+7)$

31)$(7 r-5 t)^{2}$

Відповідь

$49 r^{2}-70 r t+25 t^{2}$

32)$(11 u-9 w)^{2}$

33)$(5 b+6 c)(3 b-2 c)$

Відповідь

$15 b^{2}+8 b c-12 c^{2}$

34)$(3 r+2 t)(5 r-3 t)$

35)$(3 u+5 v)(3 v-5 v)$

Відповідь

$9 u^{2}-25 v^{2}$

36)$(11 a+4 c)(11 a-4 c)$

37)$\left(9 b^{3}+10 c^{5}\right)\left(9 b^{3}-10 c^{5}\right)$

Відповідь

$81 b^{6}-100 c^{10}$

38)$\left(9 r^{5}+7 t^{2}\right)\left(9 r^{5}-7 t^{2}\right)$

39)$(9 s-4 t)(9 s+4 t)$

Відповідь

$81 s^{2}-16 t^{2}$

40)$(12 x-7 y)(12 x+7 y)$

41)$(7 x-9 y)(7 x+9 y)$

Відповідь

$49 x^{2}-81 y^{2}$

42)$(10 r-11 t)(10 r+11 t)$

43)$(6 a-6 b)(2 a+3 b)$

Відповідь

$12 a^{2}+6 a b-18 b^{2}$

44)$(6 r-5 t)(2 r+3 t)$

45)$(10 x-10)(10 x+10)$

Відповідь

$100 x^{2}-100$

46)$(12 x-8)(12 x+8)$

47)$(4 a+2 b)(6 a-3 b)$

Відповідь

$24 a^{2}-6 b^{2}$

48)$(3 b+6 c)(2 b-4 c)$

49)$(5 b-4 c)(3 b+2 c)$

Відповідь

$15 b^{2}-2 b c-8 c^{2}$

50)$(3 b-2 c)(4 b+5 c)$

51)$(4 b-6 c)(6 b-2 c)$

Відповідь

$24 b^{2}-44 b c+12 c^{2}$

52)$(4 y-4 z)(5 y-3 z)$

53)$\left(11 r^{5}+9 t^{2}\right)^{2}$

Відповідь

$121 r^{10}+198 r^{5} t^{2}+81 t^{4}$

54)$\left(11 x^{3}+10 z^{5}\right)^{2}$

55)$(4 u-4 v)(2 u-6 v)$

Відповідь

$8 u^{2}-32 u v+24 v^{2}$

56)$(4 u-5 w)(5 u-6 w)$

57)$\left(8 r^{4}+7 t^{5}\right)^{2}$

Відповідь

$64 r^{8}+112 r^{4} t^{5}+49 t^{10}$

58)$\left(2 x^{5}+5 y^{2}\right)^{2}$

59)$(4 r+3 t)(4 r-3 t)$

Відповідь

$16 r^{2}-9 t^{2}$

60)$(3 r+4 s)(3 r-4 s)$

61)$(5 r+6 t)^{2}$

Відповідь

$25 r^{2}+60 r t+36 t^{2}$

62)$(12 v+5 w)^{2}$

63)$(3 x-4)(2 x+5)$

Відповідь

$6 x^{2}+7 x-20$

64)$(5 x-6)(4 x+2)$

65)$(6 b+4 c)(2 b+3 c)$

Відповідь

$12 b^{2}+26 b c+12 c^{2}$

66)$(3 v+6 w)(2 v+4 w)$

67)$\left(11 u^{2}+8 w^{3}\right)\left(11 u^{2}-8 w^{3}\right)$

Відповідь

$121 u^{4}-64 w^{6}$

68)$\left(3 u^{3}+11 w^{4}\right)\left(3 u^{3}-11 w^{4}\right)$

69)$(4 y+3 z)^{2}$

Відповідь

$16 y^{2}+24 y z+9 z^{2}$

70)$(11 b+3 c)^{2}$

71)$(7 u-2 v)^{2}$

Відповідь

$49 u^{2}-28 u v+4 v^{2}$

72)$(4 b-5 c)^{2}$

73)$(3 v+2 w)(5 v+6 w)$

Відповідь

$15 v^{2}+28 v w+12 w^{2}$

74)$(5 y+3 z)(4 y+2 z)$

75)$(5 x-3)(6 x+2)$

Відповідь

$30 x^{2}-8 x-6$

76)$(6 x-5)(3 x+2)$

Для кожного з наведених нижче малюнків обчислити площу квадрата двома методами.

1. Знайдіть площу, підсумовуючи площі її частин (див. Приклад 5.5.7).
2. Знайдіть площу, спрямувавши сторону квадрата, використовуючи квадрат біноміального ярлика.

77)

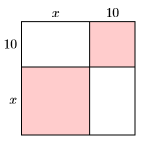
Відповідь

$A=x^{2}+20 x+100$

78)

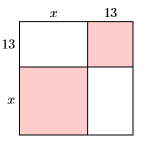
79) Квадратний шматок картону вимірює$12$ дюйми з кожного боку. Чотири квадрата, кожен має сторону$x$ дюймів, вирізаються і видаляються з кожного з чотирьох кутів квадратного шматка картону. Потім сторони складаються вздовж пунктирних ліній, щоб утворити коробку без верху.

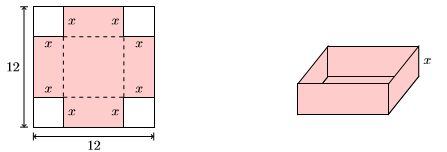
1. Знайти обсяг коробки в залежності від того$x$, міра сторони кожного квадрата, відрізаного від чотирьох куточків вихідного шматка картону. Помножте, щоб розмістити свою відповідь у стандартній формі многочлена, максимально спрощуючи вашу відповідь.
2. За допомогою отриманого полінома визначити обсяг коробки, якщо з кожного кута вихідного шматка картону вирізаються квадрати довжиною$1.25$ дюймів. Округлите відповідь до найближчого кубічного дюйма.

Відповідь

1. $V(x)=144 x-48 x^{2}+4 x^{3}$
2. $V(1.25) \approx 113$кубічних дюймів

80) Розглянемо знову коробку, утворену у вправі 79.

1. Знайдіть площу поверхні коробки в залежності від того$x$, міра сторони кожного квадрата, вирізаного з чотирьох куточків вихідного шматка картону. Помножте, щоб розмістити свою відповідь у стандартній формі многочлена, максимально спрощуючи вашу відповідь.
2. За допомогою отриманого полінома визначити площу поверхні коробки, якщо з кожного кута вихідного шматка картону вирізаються квадрати довжиною$1.25$ дюймів. Округліть відповідь до найближчого квадратного дюйма.