5.4: Множення многочленів
- Page ID
- 59514
До кінця цього розділу ви зможете:
- Помножити мономи
- Помножити многочлен на мономіал
- Помножити біноміал на біноміал
- Множимо многочлен на многочлен
- Помножте спеціальні продукти
- Множення поліноміальних функцій
Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.
- Розподілити:\(2(x+3)\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Спрощення: а.\(9^2\) б.\((−9)^2\) с\(−9^2\).
Якщо ви пропустили цю проблему, перегляньте [посилання]. - Оцініть:\(2x^2−5x+3\) для\(x=−2\).
Якщо ви пропустили цю проблему, перегляньте [посилання].
Множення мономіалів
Ми готові виконувати операції над многочленами. Оскільки мономи - це алгебраїчні вирази, ми можемо використовувати властивості експонент для множення мономов.
Помножити:
- \((3x^2)(−4x^3)\)
- \(\left(\frac{5}{6}x^3y\right)(12xy^2).\)
- Відповідь на
-
\(\begin{array} {ll} {} &{(3x^2)(−4x^3)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{3·(−4)·x^2·x^3} \\ {\text{}} &{−12x^5} \\ \end{array} \)
- Відповідь б
-
\(\begin{array} {ll} {} &{\left(\frac{5}{6}x^3y\right)(12xy^2)} \\ {\text{Use the Commutative Property to rearrange the terms.}} &{\frac{5}{6}·12·x^3·x·y·y^2} \\ {\text{Multiply.}} &{10x^4y^3} \\ \end{array} \)
Помножити:
- \((5y^7)(−7y^4)\)
- \((25a^4b^3)(15ab^3)\)
- Відповідь на
-
\(−35y^{11}\)
- Відповідь б
-
\(375 a^5b^6\)
Помножити:
- \((−6b^4)(−9b^5)\)
- \((23r^5s)(12r^6s^7).\)
- Відповідь на
-
\(54b^9\)
- Відповідь б
-
\(276 r^{11}s^8\)
Помножити многочлен на мономіал
Множення многочлена на мономіал - це насправді просто застосування розподільної властивості.
Помножити:
- \(−2y(4y^2+3y−5)\)
- \(3x^3y(x^2−8xy+y^2)\).
- Відповідь на
-
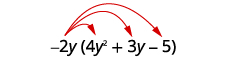
Розподілити. 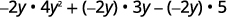
Помножити. 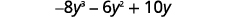
- Відповідь б
-
\(\begin{array} {ll} {} &{3x^3y(x^2−8xy+y^2)} \\ {\text{Distribute.}} &{3x^3y⋅x^2+(3x^3y)⋅(−8xy)+(3x^3y)⋅y^2} \\ {\text{Multiply.}} &{3x^5y−24x^4y^2+3x^3y^3} \\ \end{array} \)
Помножити:
- \(-3y(5y^2+8y^{7})\)
- \(4x^2y^2(3x^2−5xy+3y^2)\)
- Відповідь на
-
\(−15y^3−24y^8\)
- Відповідь б
-
\(12x^4y^2−20x^3y^3+12x^2y^4\)
Помножити:
- \(4x^2(2x^2−3x+5)\)
- \(−6a^3b(3a^2−2ab+6b^2)\)
- Відповідь на
-
\(8x^4−12x^3+20x^2\)
- Відповідь б
-
\(−18a^5b+12a^4b^2−36a^3b^3\)
Помножте біноміал на біноміал
Подібно до того, як існують різні способи представлення множення чисел, існує кілька методів, які можуть бути використані для множення біноміального на біноміальне число. Ми почнемо з використання розподільної властивості.
Помножити:
- \((y+5)(y+8)\)
- \((4y+3)(2y−5)\).
- Відповідь
-
ⓐ
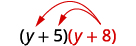
Розподілити\((y+8)\). 
Розподіліть ще раз. 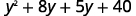
Поєднуйте подібні терміни. 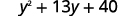
ⓑ
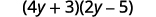
Розподілити. 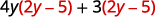
Розподіліть ще раз. 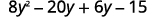
Поєднуйте подібні терміни. 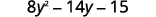
Помножити:
- \((x+8)(x+9)\)
- \((3c+4)(5c−2)\).
- Відповідь на
-
\(x^2+17x+72\)
- Відповідь б
-
\(15c^2+14c−8\)
Помножити:
- \((5x+9)(4x+3)\)
- \((5y+2)(6y−3)\).
- Відповідь на
-
\(20x^2+51x+27\)
- Відповідь б
-
\(30y^2−3y−6\)
Якщо ви розмножуєте біноміали досить часто, ви можете помітити закономірність. Зверніть увагу, що перший член в результаті є добутком перших членів у кожному біноміале. Другий і третій члени є добутком множення двох зовнішніх членів, а потім двох внутрішніх членів. І останній термін є результатом множення двох останніх термінів,
Ми скорочуємо «Перший, Зовнішній, Внутрішній, Останній» як FOIL. Букви позначають «Перший, Зовнішній, Внутрішній, Останній». Ми використовуємо це як ще один метод множення біноміалів. Слово FOIL легко запам'ятати і гарантує, що ми знаходимо всі чотири продукти.
Давайте множимо\((x+3)(x+7)\) за допомогою обох методів.

Нижче ми підсумуємо кроки методу FOIL. Метод FOIL застосовується лише до множення бічленів, а не інших поліномів!

Коли ви множите методом FOIL, малювання ліній допоможе вашому мозку зосередитися на візерунку і полегшить його нанесення.
Тепер ми зробимо приклад, де ми використовуємо шаблон FOIL для множення двох біноміалів.
Помножити:
- \((y−7)(y+4)\)
- \((4x+3)(2x−5)\).
- Відповідь
-
а.

б.

Помножити:
- \((x−7)(x+5)\)
- \((3x+7)(5x−2)\).
- Відповідь
-
а.\(x^2−2x−35\)
б.\(15x^2+29x−14\)
Помножити:
- \((b−3)(b+6)\)
- \((4y+5)(4y−10)\).
- Відповідь
-
а.\(b^2+3b−18\)
б.\(16y^2−20y−50\)
Кінцевими продуктами в останньому прикладі були тріноміали, оскільки ми могли поєднати два середні терміни. Це не завжди так.
Помножити:
- \((n^2+4)(n−1)\)
- \((3pq+5)(6pq−11)\).
- Відповідь
-
а.
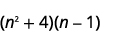
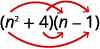
Крок 1. Помножте Перші члени. 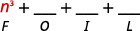
Крок 2. Помножте Зовнішні члени. 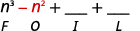
Крок 3. Помножте Внутрішні члени. 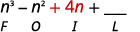
Крок 4. Помножте Останні члени. 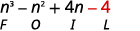
Крок 5. Поєднуйте як терміни - їх немає. 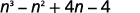
б.
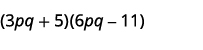
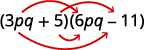
Крок 1. Помножте Перші члени. 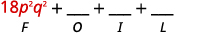
Крок 2. Помножте Зовнішні члени. 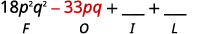
Крок 3. Помножте Внутрішні члени. 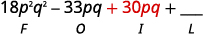
Крок 4. Помножте Останні члени. 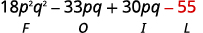
Крок 5. Поєднуйте подібні терміни. 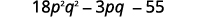
Помножити:
- \((x^2+6)(x−8)\)
- \((2ab+5)(4ab−4)\).
- Відповідь
-
а.\(x^3−8x^2+6x−48\)
б.\(8a^2b^2+12ab−20\)
Помножити:
- \((y^2+7)(y−9)\)
- \((2xy+3)(4xy−5)\).
- Відповідь
-
а.\(y^3−9y^2+7y−63\)
б.\(8x^2y^2+2xy−15\)
Метод FOIL, як правило, є найшвидшим методом множення двох біноміалів, але він працює лише для біноміалів. Ви можете використовувати Дистрибутивну властивість, щоб знайти добуток будь-яких двох поліномів. Ще один метод, який працює для всіх поліномів, - це Вертикальний метод. Це дуже схоже на метод, який ви використовуєте для множення цілих чисел. Подивіться уважно на цей приклад множення двозначних чисел.

Тепер ми застосуємо цей же метод, щоб помножити два біноміали.
Множення за допомогою вертикального методу:\((3y−1)(2y−6)\).
- Відповідь
-
Неважливо, який біном йде на верхівці.
\ (\ begin {align*} & &\ quad\;\;\; 3y - 1\\ [4pt]
& &\ підкреслення {\ quad\ times\; 2y-6}\\ [4pt]
&\ text {множити} 3y-1\ текст {на} -6. & &\ quad -18y + 6 &\ текст {частковий добуток}\\ [4pt]
&\ text {множити} 3y-1\ текст {на} 2y. &\ підкреслювати {6y^2 - 2y} &\ text {частковий продукт}\\ [4pt]
&\ text {Додати подібні терміни.} & 6y^2 - 20y + 6\ кінець {вирівнювати*}\)Зверніть увагу, що часткові продукти такі ж, як терміни в методі FOIL.
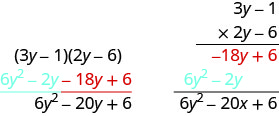
Множення за допомогою вертикального методу:\((5m−7)(3m−6)\).
- Відповідь
-
\(15m^2−51m+42\)
Множення за допомогою вертикального методу:\((6b−5)(7b−3)\).
- Відповідь
-
\(42b^2−53b+15\)
Зараз ми використали три методи множення біноміалів. Обов'язково практикуйте кожен метод, і спробуйте вирішити, який з них ви віддаєте перевагу. Методи перераховані тут всі разом, щоб допомогти вам їх запам'ятати.
Щоб помножити біноміали, використовуйте:
- Розподільна власність
- Фольга метод
- вертикальний метод
Помножити многочлен на многочлен
Ми помножили мономи на мономи, мономи на многочлени та біноми на біноми. Тепер ми готові помножити многочлен на многочлен. Пам'ятайте, що FOIL не буде працювати в цьому випадку, але ми можемо використовувати або властивість Distributive, або вертикальний метод.
Множення,\((b+3)(2b^2−5b+8)\) використовуючи ⓐ розподільну властивість і ⓑ вертикальний метод.
- Відповідь
-
а.
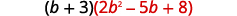
Розподілити. 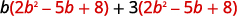
Помножити. 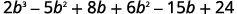
Поєднуйте подібні терміни. 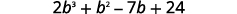
б Легше поставити многочлен з меншою кількістю членів на дні, оскільки таким чином ми отримуємо менше часткових продуктів.
\((2b^2−5b+8)\)Помножте на 3.
Помножити\((2b^2−5b+8)\) на\(b\).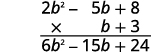
Додайте подібні терміни. 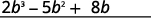
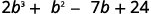
Множення,\((y−3)(y^2−5y+2)\) використовуючи ⓐ розподільну властивість і ⓑ вертикальний метод.
- Відповідь
-
а.\(y^3−8y^2+17y−6\)
б.\(y^3−8y^2+17y−6\)
Множення,\((x+4)(2x^2−3x+5)\) використовуючи а) розподільну властивість і б) вертикальний метод.
- Відповідь
-
а. і б.\(2x^3+5x^2−7x+20\)
Зараз ми побачили два методи, які можна використовувати для множення многочлена на многочлен. Після того, як ви практикуєте кожен метод, ви, ймовірно, знайдете, що ви віддаєте перевагу одному шляху над іншим. Ми перерахуємо обидва методи, перераховані тут, для зручності довідки.
Щоб помножити триноміал на біноміал, використовуйте:
- Розподільна власність
- вертикальний метод
Помножити спеціальні продукти
Математики люблять шукати закономірності, які полегшать їх роботу. Хорошим прикладом цього є квадратні двочлени. Хоча ви завжди можете отримати продукт, написавши біноміал двічі та помноживши їх, менше роботи, якщо ви навчитеся використовувати візерунок. Почнемо з розгляду трьох прикладів і пошукаємо викрійку.
Подивіться на ці результати. Ви бачите якісь візерунки?
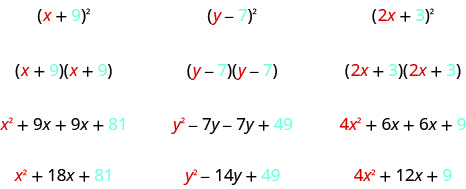
А як щодо кількості термінів? У кожному прикладі ми склали біноміал, і результат був триноміальним.
\[(a+b)^2=\text{___}+\text{___}+\text{___} \nonumber\]
Тепер подивіться на перший термін в кожному результаті. Звідки воно взялося?
Перший термін - це добуток перших членів кожного біноміала. Оскільки біноміали ідентичні, це просто квадрат першого члена!
\[(a+b)^2=a^2+\text{___}+\text{___} \nonumber\]
Щоб отримати перший термін виробу, квадратний перший член.
Звідки взявся останній термін? Подивіться приклади і знайдіть викрійку.
Останній термін - добуток останніх термінів, який є квадратом останнього члена.
\[(a+b)^2=\text{___}+\text{___}+b^2 \nonumber\]
Щоб отримати останній термін виробу, квадратний останній термін.
Нарешті, подивіться на середній термін. Зверніть увагу, що це сталося з додавання «зовнішнього» та «внутрішнього» термінів - які однакові! Таким чином, середній термін є подвійним добутком двох членів біноміального.
\[(a+b)^2=\text{___}+2ab+\text{___} \nonumber\]
\[(a−b)^2=\text{___}−2ab+\text{___} \nonumber\]
Щоб отримати середній термін добутку, помножте добуток і подвоюйте їх добуток.
Збираємо все разом:
Якщо a і b є дійсними числами,

Для квадратного двочлена, квадрат першого члена, квадрат останнього члена, подвоїти їх добуток.
Множимо: а.\((x+5)^2\) б\((2x−3y)^2\).
- Відповідь
-
а.
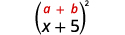
Квадратний перший член. 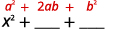
Квадратний останній термін. 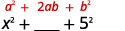
Подвоїти свій продукт. 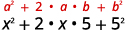
Спростити. 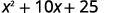
б.
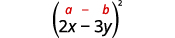
Використовуйте викрійку. 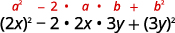
Спростити. 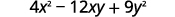
Множимо: а.\((x+9)^2\) б\((2c−d)^2\).
- Відповідь
-
а.\(x^2+18x+81\)
б.\(4c^2−4cd+d^2\)
Множимо: а.\((y+11)^2\) б\((4x−5y)^2\).
- Відповідь
-
а.\(y^2+22y+121\)
б.\(16x^2−40xy+25y^2\)
Ми щойно побачили шаблон для квадратування бічленів, який ми можемо використовувати, щоб полегшити множення деяких біноміалів. Аналогічно існує візерунок і для іншого твору біноміалів. Але перш ніж ми перейдемо до цього, нам потрібно ввести певний словниковий запас.
Пара біноміалів, кожен з яких має однаковий перший член і той самий останній член, але один - сума, а один - різниця називається сполученою парою і має форму\((a−b)\),\((a+b)\).
Спряжена пара - це два двочлени виду
\[(a−b), (a+b). \nonumber\]
Пара біноміалів має один і той же перший член і той самий останній член, але один біноміал - це сума, а інший - різниця.
Існує приємний візерунок для знаходження твору кон'югатів. Ви могли б, звичайно, просто ФОЛЬГА, щоб отримати продукт, але використання візерунка полегшує вашу роботу. Давайте подивимося на візерунок, використовуючи FOIL для множення деяких сполучених пар.
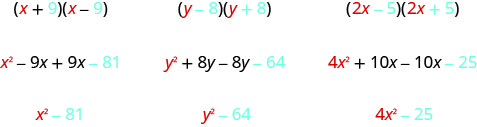
Що ви спостерігаєте щодо продуктів?
Твір двох біноміалів також є біноміальним! Більшість продуктів, отриманих з ФОЛЬГИ, були тріноміалами.
Кожен перший член є добутком перших членів біноміалів, а оскільки вони ідентичні, це квадрат першого члена.
\[(a+b)(a−b)=a^2−\text{___} \nonumber\]
Щоб отримати перший член, зробіть квадрат першого члена.
Останній термін прийшов з множення останніх членів, квадрата останнього члена.
\[(a+b)(a−b)=a^2−b^2 \nonumber\]
Щоб отримати останній термін, квадратний останній член.
Чому немає середнього терміну? Зверніть увагу на два середні члени, які ви отримуєте від FOIL об'єднати до 0 у кожному випадку, результат одного додавання та одного віднімання.
Твір кон'югатів завжди має форму\(a^2−b^2\). Це називається різницею квадратів.
Це призводить до закономірності:
Якщо a і b є дійсними числами,

Твір називається різницею квадратів.
Для множення сполучених, квадрат першого члена, квадрат останнього члена, запишіть його як різницю квадратів.
Множимо за допомогою добутку сполучених візерунків: а.\((2x+5)(2x−5)\) б\((5m−9n)(5m+9n)\).
- Відповідь
-
а.
Чи є біноміали кон'югати? 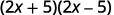
Це твір кон'югатів. 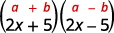
Квадрат першого члена, 2х.2х. 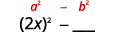
Квадрат останнього члена, 5.5. 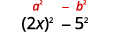
Спростити. Твір являє собою різницю квадратів. 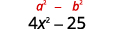
б.
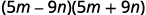
Це підходить до викрійки. 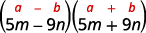
Використовуйте викрійку. 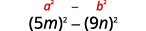
Спростити. 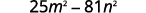
Множимо: а.\((6x+5)(6x−5)\) б\((4p−7q)(4p+7q)\).
- Відповідь
-
а.\(36x^2−25\)
б.\(16p^2−49q^2\)
Множимо: а.\((2x+7)(2x−7)\) б\((3x−y)(3x+y)\).
- Відповідь
-
а.\(4x^2−49\) б.\(9x^2−y^2\)
Ми тільки що розробили спеціальні шаблони продуктів для біноміальних квадратів і для добутку кон'югатів. Вироби виглядають аналогічно, тому важливо визнати, коли доречно використовувати кожен з цих візерунків і помітити, чим вони відрізняються. Подивіться на дві моделі разом і зверніть увагу на їх подібності та відмінності.
| Біноміальні квадрати | добуток кон'югатів |
|---|---|
| \((a+b)^2=a^2+2ab+b^2\) | \((a−b)(a+b)=a^2−b^2\) |
| \((a−b)^2=a^2−2ab+b^2\) | |
| • Квадратне біноміальне | • Множення кон'югатів |
| • Продукт є тріноміалом | • Продукт є біноміальним. |
| • Внутрішні та зовнішні терміни з FOIL однакові. | • Внутрішні та зовнішні терміни з фольгою є протилежними. |
| • Середній термін є подвійним добутком термінів | • Середнього терміну немає. |
Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:
а.\((2x−3)(2x+3)\) б. в.\((8x-5)^2\)\((6m+7)^2\) д\((5x−6)(6x+5)\).
- Відповідь
-
а.\((2x−3)(2x+3)\)
Це кон'югати. Вони мають однакові перші числа, і ті ж останні числа, і один біноміал - це сума, а інший - різниця. Він підходить до виробу з кон'югатів візерунком.
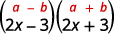
Використовуйте викрійку. 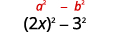
Спростити. 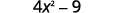
б.\((8x−5)^2\)
Нас просять квадратний двочлен. Він підходить для візерунка біноміальних квадратів.
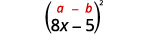
Використовуйте викрійку. 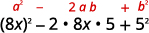
Спростити. 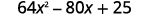
c.\((6m+7)^2\)
Знову ж таки, ми будемо квадратувати біном, тому ми використовуємо шаблон біноміальних квадратів.
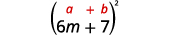
Використовуйте викрійку. 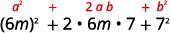
Спростити. 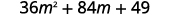
д.\((5x−6)(6x+5)\)
Цей виріб не підходить по викрійках, тому будемо використовувати фольгу.
\(\begin{array} {ll} {} &{(5x−6)(6x+5)} \\ {\text{Use FOIL.}} & {30x^2+25x−36x−30} \\ {\text{Simplify.}} & {30x^2−11x−30} \\ \end{array}\)
Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:
а.\((9b−2)(2b+9)\) б. в.\((9p−4)^2\)\((7y+1)^2\) д\((4r−3)(4r+3)\).
- Відповідь
-
а. фольга;\(18b^2+77b−18\)
б. біноміальні квадрати;\(81p^2−72p+16\)
с. біноміальні квадрати;\(49y^2+14y+1\)
d. добуток кон'югатів;\(16r^2−9\)
Виберіть відповідний візерунок і використовуйте його, щоб знайти виріб:
а.\((6x+7)^2\) б. в.\((3x−4)(3x+4)\)\((2x−5)(5x−2)\) д\((6n−1)^2\).
- Відповідь
-
а. біноміальні квадрати;\(36x^2+84x+49\) б. добуток кон'югатів;\(9x^2−16\) c. фольга;\(10x^2−29x+10\) d. біноміальні квадрати;\(36n^2−12n+1\)
Множення многочленних функцій
Подібно до того, як многочлени можна множити, поліноміальні функції також можна множити.
Для функцій\(f(x)\) і\(g(x)\),
\[(f·g)(x)=f(x)·g(x)\]
Для функцій\(f(x)=x+2\) і\(g(x)=x^2−3x−4\), знайдіть:
- \((f·g)(x)\)
- \((f·g)(2)\).
- Відповідь
-
а.
\(\begin{array} {ll} {} &{(f·g)(x)=f(x)·g(x)} \\ {\text{Substitute for } f(x) \text{ and } g(x)} &{(f·g)(x)=(x+2)(x^2−3x−4)} \\ {\text{Multiply the polynomials.}} &{(f·g)(x)=x(x^2−3x−4)+2(x^2−3x−4)} \\ {\text{Distribute.}} &{(f·g)(x)=x3−3x^2−4x+2x^2−6x−8} \\ {\text{Combine like terms.}} &{(f·g)(x)=x3−x^2−10x−8} \\ \end{array}\)
б. частково a. ми знайшли\((f·g)(x)\) і тепер просять знайти\((f·g)(2)\).
\(\begin{array} {ll} {} &{(f·g)(x)=x^3−x^2−10x−8} \\ {\text{To find }(f·g)(2), \text{ substitute } x=2.} &{(f·g)(2)=2^3−2^2−10·2−8} \\ {} &{(f·g)(2)=8−4−20−8} \\ {} &{(f·g)(2)=−24} \\ \end{array}\)
Для функцій\(f(x)=x−5\) і\(g(x)=x^2−2x+3\), знайти
- \((f·g)(x)\)
- \((f·g)(2)\).
- Відповідь на
-
\((f·g)(x)=x^3−7x^2+13x−15\)
- Відповідь б
-
\((f·g)(2)=−9\)
Для функцій\(f(x)=x−7\) і\(g(x)=x^2+8x+4\), знайти
- \((f·g)(x)\)
- \((f·g)(2)\).
- Відповідь на
-
\((f·g)(x)=x^3+x^2−52x−28\)
- Відповідь на
-
\((f·g)(2)=−120\)
Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з множенням поліномів.
- Знайомство зі спеціальними продуктами біноміалів
Ключові поняття
- Як використовувати метод FOIL для множення двох біноміалів.
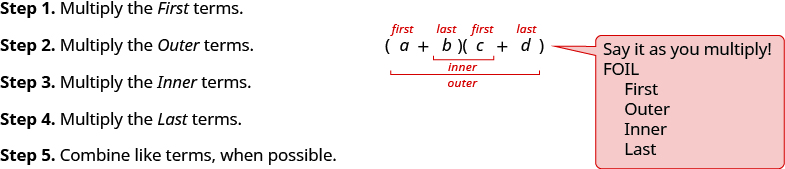
- Множення двох біноміалів: Щоб помножити біноміали, використовуйте:
- Розподільна власність
- Фольга метод
- Множення многочлена на многочлен: Щоб помножити триноміал на біноміал, використовуйте:
- Розподільна власність
- вертикальний метод
- Візерунок біноміальних квадратів
Якщо a і b є дійсними числами,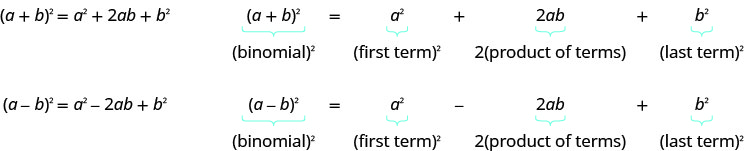
- Твір сполучених візерунків
Якщо a, b -
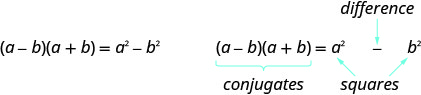
дійсні числа Твір називається різницею квадратів.
Для множення сполучених, квадрат першого члена, квадрат останнього члена, запишіть його як різницю квадратів. - Порівняння спеціальних моделей продукту
Біноміальні квадрати добуток кон'югатів \((a+b)^2=a^2+2ab+b^2\) \((a−b)^2=a^2−2ab+b^2\) \((a−b)(a+b)=a^2−b^2\) • Квадратне біноміальне • Множення кон'югатів • Продукт є тріноміалом • Продукт є біноміальним. • Внутрішні та зовнішні терміни з FOIL однакові. • Внутрішні та зовнішні терміни з фольгою є протилежними. • Середній термін є подвійним добутком термінів • Середнього терміну немає. - Множення поліноміальних функцій:
- Для функцій\(f(x)\) і\(g(x)\),
\[(f⋅g)(x)=f(x)⋅g(x) \nonumber\]
- Для функцій\(f(x)\) і\(g(x)\),
Глосарій
- сполучені пари
- Спряжена пара - це два бічлена виду\((a−b)\) і\((a+b)\). Пара біноміалів має один і той же перший член і той самий останній член, але один біноміал - це сума, а інший - різниця.
