5.3: Застосування поліномів

У цьому розділі досліджуються реальні застосування поліноміальних функцій.

Приклад$\PageIndex{1}$

Середня ціна галона газу на початок кожного місяця за період, що починається в листопаді 2010 року і закінчується в травні 2011 року, наведені в маржі. Дані побудовані на малюнку$\PageIndex{1}$ та розміщені наступним поліномом третього ступеня, де t - кількість місяців, що минули з жовтня 2010 року.

$$p(t)=-0.0080556 t^{3}+0.11881 t^{2}-0.30671 t+3.36 \label{Eq5.3.1}$$

Скористайтеся графіком, а потім поліномом, щоб оцінити ціну галона газу в Каліфорнії в лютому 2011 року.

Малюнок$\PageIndex{1}$: Встановлення ціни на газ проти місяця з кубічним поліномом.

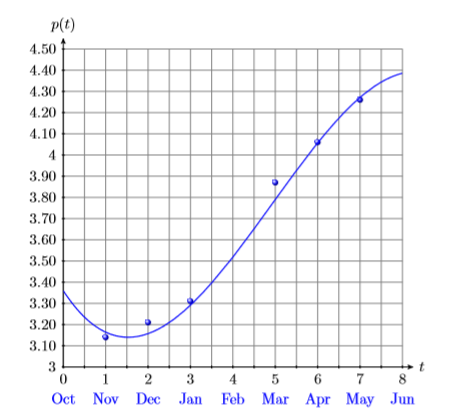
$$\begin{array}{c|c}\hline \text { Month } & {\text { Price }} \\ \hline \text { Nov. } & {3.14} \\ {\text { Dec. }} & {3.21} \\ {\text { Jan }} & {3.31} \\ {\text { Mar. }} & {3.87} \\ {\text { Apr. }} & {4.06} \\ {\text { May }} & {4.26} \\ \hline\end{array} \nonumber$$

Рішення

Знайдіть лютий ($t = 4$) на горизонтальній осі. Звідти намалюйте вертикальну стрілку вгору до графіка, а від цієї точки перетину - другу горизонтальну стрілку до вертикальної осі (див.$\PageIndex{2}$ Рис. Здавалося б, ціна за галон у лютому була приблизно$\$3.51$.

Рисунок$\PageIndex{2}$: Орієнтовна ціна газу протягом лютого.

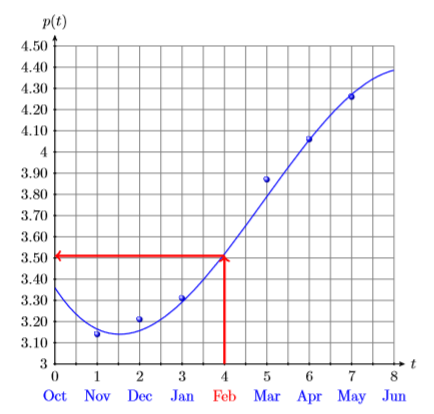
Далі ми будемо використовувати придатний поліном третього ступеня, щоб наблизити ціну за галон за лютий 2011 року. Почніть з функції, визначеної за допомогою Equation\ ref {Eq5.3.1}, і$4$ замініть$t$.

$$\begin{aligned} p(t) &=-0.0080556 t^{3}+0.11881 t^{2}-0.30671 t+3.36 \\ p(4) &=-0.0080556(4)^{3}+0.11881(4)^{2}-0.30671(4)+3.36 \end{aligned} \nonumber$$

Використовуйте калькулятор для оцінки$p(4)$ (див. Малюнок$\PageIndex{3}$). Округлення до найближчого

Малюнок$\PageIndex{3}$: Оцінка$p(4)$.

копійки, ціна в лютому була$\$3.52$ за галон.

Приклад$\PageIndex{2}$

Якщо снаряд потрапляє в повітря, його висота над землею в будь-який момент задається формулою

$$y=y_{0}+v_{0} t-\dfrac{1}{2} g t^{2} \label{Eq5.3.2}$$

де

$y$= висота над землею в той час$t$

$y_0$= початкова висота над землею в той час$t = 0$

$v_0$= початкова швидкість в часі$t = 0$

$g$= прискорення за рахунок сили тяжіння

$t$= час минув з моменту стрільби снаряда

Якщо снаряд запущений з початковою швидкістю$100$ метрів в секунду ($100$м/с) з даху$8$ метрів ($8$м) над рівнем землі, то в який час снаряд першим досягне висоти$400$ метрів ($400$м)? Примітка: Біля земної поверхні прискорення за рахунок сили тяжіння становить приблизно$9.8$ метри в секунду ($9.8$(м/с) /с або$9.8$ м/с ²).

Рішення

Наведено початкову висоту$y_0 = 8$ m, початкова швидкість$v_0 = 100$ м/с, а прискорення за рахунок сили тяжіння -$g =9.8$ м/с ². Підставте ці значення в Equation\ ref {Eq5.3.2}, а потім спростіть отримання наступного результату:

$$\begin{array}{l}{y=y_{0}+v_{0} t-\dfrac{1}{2} g t^{2}} \\ {y=8+100 t-\dfrac{1}{2}(9.8) t^{2}} \\ {y=8+100 t-4.9 t^{2}}\end{array} \nonumber$$

Введіть$y=8+100 t-4.9 t^{2}$ як$\mathbf{Y} \mathbf{1}=\mathbf{8}+100^{*} \mathbf{X}-4.9^{*} \mathbf{X} \wedge \mathbf{2}$ у меню Y= (див. Перше зображення на малюнку$\PageIndex{4}$). Після деяких експериментів ми зупинилися на параметрах WINDOW, показаних на другому зображенні на рис$\PageIndex{4}$. Натисніть кнопку GRAPH, щоб створити графік,$y=8+100 t-4.9 t^{2}$ показаний на третьому малюнку Рисунок$\PageIndex{4}$.

У цьому прикладі горизонтальна вісь насправді є$t$-axis. So when we set $\mathrm{Xmin}$ and $\mathrm{Xmax}$, we’re actually setting bounds on the $t$-axis.

Малюнок$\PageIndex{4}$: Ескіз графіка$y = 8 + 100t−4.9t^2$.

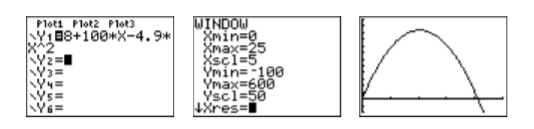
Щоб знайти, коли снаряд досягне висоти$400$ метрів ($400$м), замінюємо$400$$y$ на отримання:

$$400=8+100 t-4.9 t^{2} \label{Eq5.3.3}$$

Введіть ліву частину Equation\ ref {Eq5.3.3}$\mathbf{Y} \boldsymbol{2}$ в меню Y=, як показано на першому зображенні на малюнку$\PageIndex{5}$. Натисніть кнопку GRAPH, щоб отримати результат, показаний на другому зображенні на малюнку$\PageIndex{5}$. Зверніть увагу, що є дві точки перетину, що має сенс, оскільки снаряд потрапляє на$400$ метри на шляху вгору і$400$ метрів на шляху вниз.

Малюнок$\PageIndex{5}$: Визначення, коли об'єкт вперше досягає$400$ метрів.

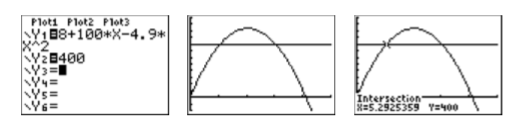
Щоб знайти першу точку перетину, виберіть 5:intersect з меню CALC. Натисніть ENTER у відповідь на «Перша крива», потім натисніть клавішу ENTER ще раз у відповідь на «Друга крива». Для вашої здогадки використовуйте клавіші зі стрілками, щоб перемістити курсор ближче до першої точки перетину, ніж до другої. У цей момент натисніть ENTER у відповідь на «Вгадати». Результат показаний на третьому зображенні на рис$\PageIndex{5}$. Снаряд спочатку досягає висоти$400$ метрів приблизно через$5.2925359$ секунди після запуску.

Малюнок$\PageIndex{6}$: Повідомлення про графічне рішення на домашнє завдання.

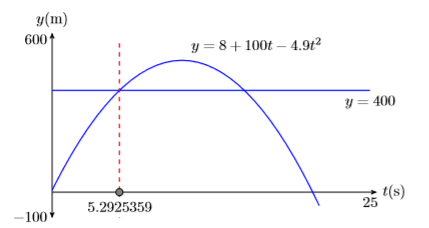
Парабола, показана на малюнку$\PageIndex{6}$ is not the actual flight path of the projectile. The graph only predicts the height of the projectile as a function of time.

Повідомлення про рішення домашнього завдання: Дублюйте зображення у вікні перегляду калькулятора на сторінці домашнього завдання. Використовуйте лінійку, щоб намалювати всі лінії, але від руки будь-які криві.

• Позначте горизонтальну і вертикальну$t$ осі і$y$ відповідно (див.$\PageIndex{6}$ Рис. Включити одиниці (секунди) і метри (м)).
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{6}$). Включити одиниці (секунди) і метри (м)).
• Позначте кожен граф своїм рівнянням (див. Малюнок$\PageIndex{6}$).
• Намалюйте пунктирну вертикальну лінію через першу точку перетину. Затіньте і позначте точку (з її$t$ -значенням), де пунктирна вертикальна лінія перетинає$t$ вісь -. Це перше рішення рівняння$400 = 8+100t−4.9t^2$ (див. Рис.$\PageIndex{6}$).

Округлення до найближчої десятої частки секунди, снаряд займає приблизно$t ≈ 5.3$ секунди, щоб першим досягти висоти$400$ метрів.

Словосполучення «затінювати і позначити точку» означає заповнення точки на$t$-axis, then write the $t$-value of the point just below the shaded point.

Вправа$\PageIndex{2}$

Якщо снаряд запущений з початковою$60$ meters per second from a rooftop $12$ meters above ground level, at what time will the projectile швидкістю спочатку досягають висоти$150$ meters?

Відповідь

$\approx 3.0693987$секунд

Нулі та$x$ -перехоплення функції

Нагадаємо, що$f(x)$ і$y$ є взаємозамінними. Тому, якщо нас попросять знайти, де функція дорівнює нулю, то нам потрібно знайти точки на графіку функції, які мають$y$ значення -значення, рівне нулю (див. Рис.$\PageIndex{7}$).

Малюнок$\PageIndex{7}$: Розташування нулів функції.

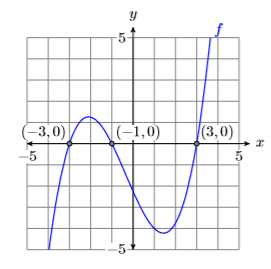
Нулі і$x$-intercepts

Точки, де графік перетинає$x$ -вісь, називаються$x$ -перехопленнями графіка$f$. $x$-value кожного$x$ -intercept називається нулем функції$f$.

Графік$f$ перетинає$x$ -вісь$\PageIndex{7}$ на малюнку в$(−3,0)$$(−1,0)$, і$(3 ,0)$. Тому:

• $x$-перехоплення f є:$(−3,0)$,$(−1,0)$, і$(3,0)$
• Нулями$f$ є:$−3$,$−1$, і$3$

Ключова ідея

Функція дорівнює нулю, де її графік перетинає$x$ вісь -.

Приклад$\PageIndex{3}$

Знайти нуль (и) функції$f(x)=1 .5x +5 .25$.

Рішення

Пам'ятайте,$f(x)=1 .5x +5 .25$ і$y =1 .5x +5 .25$ рівнозначні. Ми шукаємо значення$x$, що робить$y = 0$ або$f(x) = 0$. Отже, почнемо з$f(x) = 0$, а потім$f(x)$ замініть на$1 .5x +5 .25$.

$$\begin{aligned} f(x) &= 0 \quad \color {Red} \text { We want the value of } x \text { that makes the function equal to zero. } \\ 1.5 x+5.25 &= 0 \quad \color {Red} \text { Replace } f(x) \text { with } 1.5 x+5.25 \end{aligned} \nonumber$$

Тепер вирішуємо для$x$.

$$\begin{aligned} 1.5 x &= -5.25 \quad \color {Red} \text { Subtract } 5.25 \text { from both sides. } \\ x &= \dfrac{-5.25}{1.5} \quad \color {Red} \text { Divide both sides by } 1.5 \\ x &= -3.5 \quad \color {Red} \text { Divide: }-5.25 / 1.5=-3.5 \end{aligned} \nonumber$$

Перевірка:$−3.5$$x$ Замініть у функції$f(x)=1 .5x +5 .25$.

$$\begin{aligned} f(x) &=1.5 x+5.25 \quad \color {Red} \text { The original function. } \\ f(-3.5) &=1.5(-3.5)+5.25 \quad \color {Red} \text { Substitute }-3.5 \text { for } x \\ f(-3.5) &=-5.25+5.25 \quad \color {Red} \text { Multiply: } 1.5(-3.5)=-5.25 \\ f(-3.5) &=0 \quad \color {Red} \text { Add. } \end{aligned} \nonumber$$

Зверніть увагу$−3.5$, що при заміні$x$ на функцію робить$f(x)=1 .5x+5 .25$ рівну нулю. Саме тому і$−3.5$ називається нулем функції.

Рішення графічного калькулятора: Ми повинні бути в змозі знайти нуль, намалювавши графік$f$ і зазначивши, де він перетинає$x$ вісь -. Почніть з завантаження функції$f(x)=1 .5x +5 .25$$\mathbf{Y1}$ в меню Y= (див. перше зображення на малюнку$\PageIndex{8}$).

Виберіть 6:ZStandard в меню ZOOM, щоб створити графік$f$ (див. Друге зображення на малюнку$\PageIndex{8}$). Натисніть 2ND CALC, щоб відкрити меню РОЗРАХУВАТИ (див. Третє зображення на малюнку$\PageIndex{8}$). Щоб знайти нуль функції$f$:

Малюнок$\PageIndex{8}$: Знаходження нуля$f(x)=1 .5x +5 .25$.

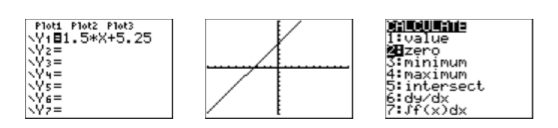
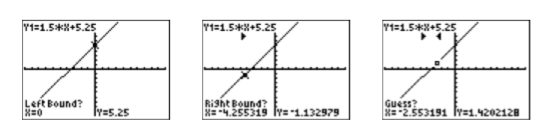
1. Виберіть 2:нуль в меню РОЗРАХУВАТИ. Калькулятор відповідає, запитуючи «Ліва межа?» (Див. Перше зображення на малюнку$\PageIndex{9}$). За допомогою кнопки зі стрілкою вліво перемістіть курсор так, щоб він лежав зліва від$x$ -перехоплення$f$ і натисніть ENTER.
2. Калькулятор відповідає, запитуючи «Right Bound?» (Див. Друге зображення на малюнку$\PageIndex{9}$). За допомогою кнопки зі стрілкою вправо перемістіть курсор так, щоб він лежав праворуч від$x$ -перехоплення$f$ і натисніть ENTER.
3. Калькулятор відповідає, запитуючи «Вгадай?» (Див. Третє зображення на малюнку$\PageIndex{9}$). Поки ваш курсор лежить між лівими та праворуч позначками у верхній частині екрана (див. Третє зображення на малюнку$\PageIndex{9}$), у вас є дійсне припущення. Оскільки курсор вже лежить між лівою та правою межами, просто натисніть ENTER, щоб використати поточне положення курсора як ваше здогадка.

Малюнок$\PageIndex{9}$: Використання 2: нуль з меню РОЗРАХУВАТИ.

Калькулятор реагує наближенням нуля функції, як показано на малюнку$\PageIndex{10}$.

Малюнок$\PageIndex{10}$: $−3.5$є нульовим вимкненням.

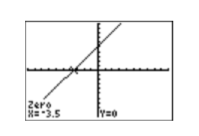
Зверніть увагу, що наближення, знайдене за допомогою калькулятора, добре узгоджується з нулем, знайденим за допомогою алгебраїчної техніки.

Вправа$\PageIndex{3}$

Знайти нуль (и) функції$f(x)=2 .6x−9.62$.

Відповідь

$3.7$

Приклад$\PageIndex{4}$

Скільки часу знадобиться снаряд у прикладі,$\PageIndex{2}$ щоб повернутися на рівень землі?

Рішення

У $\PageIndex{2}$прикладі висота снаряда над землею в залежності від часу задається рівнянням $$y = 8 + 100t−4.9t^2 \nonumber$$ Коли снаряд повертається на землю, його висота над землею буде дорівнює нулю метрів. Щоб знайти час, який це станеться, підставляємо$y = 0$ останнє рівняння і вирішуємо для$t$. $$0 = 8 + 100t−4.9t^2 \nonumber$$ Введіть рівняння$y = 8 + 100t − 4.9t^2$$\mathbf{Y1}$ в меню Y = вашого калькулятора (див. Перше зображення на малюнку$\PageIndex{11}$), а потім встановіть параметри WINDOW, показані на другому зображенні на малюнку$\PageIndex{11}$. Натисніть кнопку GRAPH, щоб створити графік функції, показаний на третьому зображенні на малюнку$\PageIndex{11}$.

Малюнок$\PageIndex{11}$: Ескіз графіка$y = 8 + 100t−4.9t^2$.

У цьому прикладі горизонтальна вісь насправді є$t$-axis. So when we set $\mathrm{Xmin}$ and $\mathrm{Xmax}$, we’re actually setting bounds on the $t$-axis.

Щоб знайти час, коли снаряд повертається на рівень землі, нам потрібно знайти, де графік$y = 8+100t−4.9t^2$ перетинає горизонтальну вісь (в даному випадку вісь t). Виберіть 2:нуль у меню CALC. За допомогою клавіш зі стрілками перемістіть курсор трохи вліво від$t$ -перехоплення, потім натисніть ENTER у відповідь на «Ліва межа». Наведіть курсор трохи праворуч від t-перехоплення, а потім натисніть ENTER у відповідь на «Праворуч». Залиште курсор там, де він знаходиться, і натисніть ENTER у відповідь на «Вгадати». Результат показаний на малюнку$\PageIndex{11}$.

• Позначте горизонтальну і вертикальну$t$ осі і$y$ відповідно (див.$\PageIndex{12}$ Рис. Включити одиниці (секунди) і метри (м)).
• Розмістіть параметри WINDOW в кінці кожної осі (див. Рис.$\PageIndex{12}$).
• Позначте графік його рівнянням (див. Малюнок$\PageIndex{12}$).
• Намалюйте пунктирну вертикальну лінію через$t$ -перехоплення. Затіньте та позначте$t$ -value точки, де пунктирна вертикальна лінія перетинає$t$ вісь -. Це рішення рівняння$0 = 8 + 100t−4.9t^2$ (див. Рис.$\PageIndex{12}$).

Малюнок$\PageIndex{12}$: Повідомлення про графічне рішення на домашнє завдання.

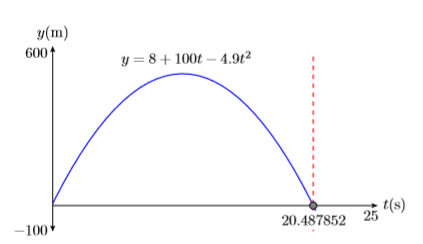
Округляючи до найближчої десятої частки секунди, снаряд займає приблизно$t ≈ 20.5$ секунди, щоб потрапити в землю.

Вправа$\PageIndex{4}$

Якщо снаряд запущений з початковою швидкістю$60$ meters per second from a rooftop $12$ meters above ground level, at what time will the projectile return to ground level?

Відповідь

$\approx 12.441734$секунд