8.3: Обернені тригонометричні функції

Цілі навчання

• Зрозумійте та використовуйте функції зворотного синуса, косинуса та дотичної.
• Знайдіть точне значення виразів із зворотними функціями синуса, косинуса та тангенса.
• Використовуйте калькулятор для оцінки обернених тригонометричних функцій.
• Знайти точні значення складових функцій з оберненими тригонометричними функціями.

Для будь-якого прямокутного трикутника, враховуючи один інший кут і довжину однієї сторони, ми можемо з'ясувати, які інші кути і сторони. Але що робити, якщо нам дано тільки дві сторони прямокутного трикутника? Потрібна процедура, яка веде нас від співвідношення сторін до кута. Тут в гру вступає поняття зворотної тригонометричної функції. У цьому розділі ми розглянемо зворотні тригонометричні функції.

Розуміння та використання функцій зворотного синуса, косинуса та тангенса

Для того, щоб використовувати зворотні тригонометричні функції, нам потрібно розуміти, що обернена тригонометрична функція «скасовує» те, що «робить» оригінальна тригонометрична функція, як це відбувається з будь-якою іншою функцією та її зворотною. Іншими словами, область оберненої функції - це діапазон вихідної функції, і навпаки, як узагальнено на малюнку$\PageIndex{1}$.

Малюнок$\PageIndex{1}$

Наприклад, якщо$f(x)=\sin\space x$, то ми б написали$f^{−1}(x)={\sin}^{−1}x$. Майте на увазі, що це${\sin}^{−1}x$ не означає$\dfrac{1}{\sin\space x}$. Наступні приклади ілюструють зворотні тригонометричні функції:

• З тих пір$\sin\left(\dfrac{\pi}{6}\right)=\dfrac{1}{2}$$\dfrac{\pi}{6}={\sin}^{−1}\left(\dfrac{1}{2}\right)$.
• З тих пір$\cos(\pi)=−1$$\pi={\cos}^{−1}(−1)$.
• З тих пір$\tan\left (\dfrac{\pi}{4}\right )=1$$\dfrac{\pi}{4}={\tan}^{−1}(1)$.

У попередніх розділах ми оцінювали тригонометричні функції під різними кутами, але часом нам потрібно знати, який кут дасть певне значення синуса, косинуса або тангенса. Для цього нам знадобляться зворотні функції. Нагадаємо, що для функції один до одного, якщо$f(a)=b$, то обернена функція задовольняла б$f^{−1}(b)=a$.

Майте на увазі, що синус, косинус і тангенс функції не є функціями один до одного. Графік кожної функції зазнає невдачі тест горизонтальної лінії. Насправді жодна періодична функція не може бути один-до-одному, оскільки кожен вихід у своєму діапазоні відповідає принаймні одному входу в кожному періоді, і існує нескінченна кількість періодів. Як і у випадку з іншими функціями, які не є один-на-один, нам потрібно буде обмежити область кожної функції, щоб отримати нову функцію, яка є один-на-один. Ми вибираємо домен для кожної функції, яка включає число 0. На малюнку$\PageIndex{2}$ показаний графік синусоїдальної функції, обмеженою до,$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ і графік функції косинуса обмеженою до$[ 0,\pi ]$.

Рисунок$\PageIndex{2}$: (a) Функція синуса на обмеженій області$\left[ −\dfrac{\pi}{2}, \dfrac{\pi}{2} \right]$; (b) Функція косинуса на обмеженій області$[ 0,\pi ]$

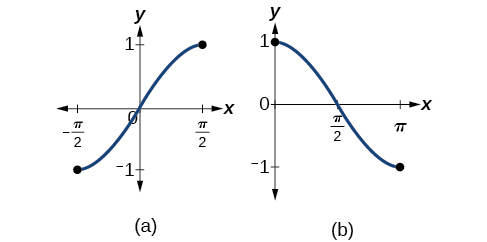
На малюнку$\PageIndex{3}$ показаний графік дотичної функції, обмеженою до$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$.

Рисунок$\PageIndex{3}$: Функція тангенса на обмеженій області$\left (−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$

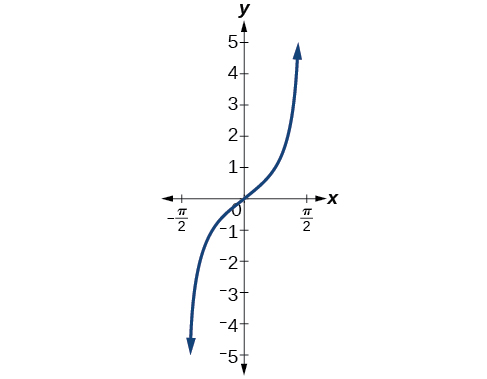
Ці звичайні варіанти для домену з обмеженим доступом є дещо довільними, але вони мають важливі, корисні характеристики. Кожен домен включає походження та деякі позитивні значення, і найголовніше, кожен призводить до функції один до одного, яка є оборотною. Звичайний вибір для обмеженої області дотичної функції також має корисну властивість, що вона поширюється від однієї вертикальної асимптоти до наступної замість того, щоб бути розділеним на дві частини асимптотою.

На цих обмежених доменах ми можемо визначити обернені тригонометричні функції.

• Функція зворотного синуса$y={\sin}^{−1}x$ означає$x=\sin\space y$. Функцію зворотного синуса іноді називають функцією арксина і позначають$\arcsin\space x$.

  $y={\sin}^{−1}x$має домен$[−1,1]$ і діапазон$\left[−\frac{\pi}{2},\frac{\pi}{2}\right]$

• Функція оберненого косинуса$y={\cos}^{−1}x$ означає$x=\cos\space y$. Функцію зворотного косинуса іноді називають функцією арккосинуса і позначають$\arccos\space x$.

  $y={\cos}^{−1}x$має домен$[−1,1]$ і діапазон$[0,π]$

• Зворотна тангенс функція$y={\tan}^{−1}x$ означає$x=\tan\space y$. Функцію оберненої дотичної іноді називають функцією арктангенса і позначають$\arctan\space x$.

  $y={\tan}^{−1}x$має домен$(−\infty,\infty)$ і діапазон$\left(−\frac{\pi}{2},\frac{\pi}{2}\right)$

Графіки обернених функцій наведені на малюнках$\PageIndex{4}$ -$\PageIndex{6}$. Зверніть увагу, що виходом кожної з цих обернених функцій є число, кут у радіановій мірі. Ми бачимо, що${\sin}^{−1}x$ має домен$[ −1,1 ]$ і діапазон$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$,${\cos}^{−1}x$ має домен$[ −1,1 ]$ і діапазон$[0,\pi]$, і${\tan}^{−1}x$ має домен всіх дійсних чисел і діапазону$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$. Щоб знайти область та діапазон обернених тригонометричних функцій, перемкніть область та діапазон вихідних функцій. Кожен графік оберненої тригонометричної функції є відображенням графіка вихідної функції про пряму$y=x$.

Малюнок$\PageIndex{4}$: Функція синуса та функція зворотного синуса (або арцинуса)

Малюнок$\PageIndex{5}$: Функція косинуса та функція оберненого косинуса (або арккосинуса)

Рисунок$\PageIndex{6}$: Функція дотичної та оберненої тангенса (або арктангенса) функції

ВІДНОСИНИ ДЛЯ ОБЕРНЕНИХ ФУНКЦІЙ СИНУСА, КОСИНУСА ТА ТАНГЕНСА

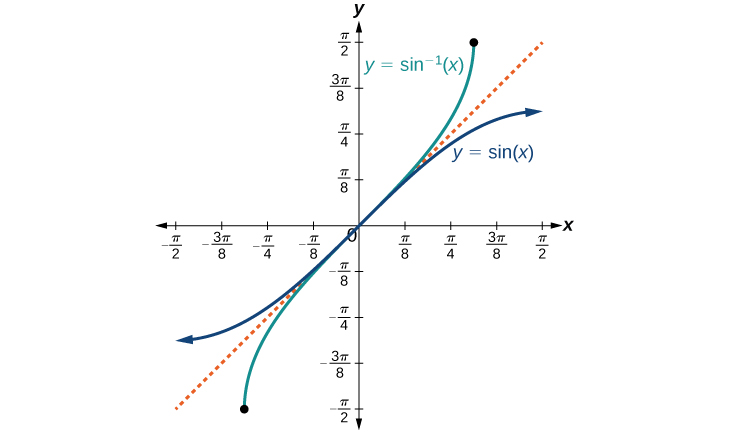
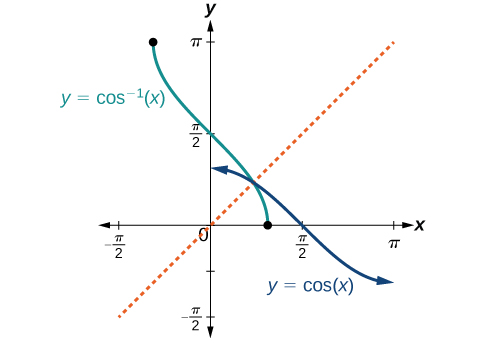
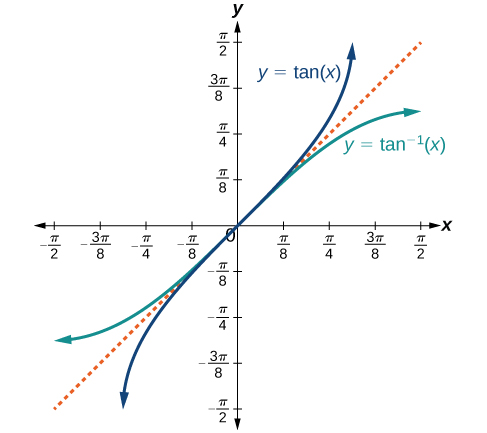
Для кутів в інтервалі$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, якщо$\sin y=x$, то${\sin}^{−1}x=y$.

Для кутів в інтервалі$[ 0,\pi ]$, якщо$\cos y=x$, то${\cos}^{−1}x=y$.

Для кутів в інтервалі$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right )$, якщо$\tan y=x$, то${\tan}^{−1}x=y$.

Приклад$\PageIndex{1}$: Writing a Relation for an Inverse Function

Задано$\sin\left(\dfrac{5\pi}{12}\right)≈0.96593$, запишіть відношення за участю оберненого синуса.

Рішення

Скористайтеся співвідношенням для зворотного синуса. Якщо$\sin y=x$, то${\sin}^{−1}x=y$.

У цій проблемі$x=0.96593$, і$y=\dfrac{5\pi}{12}$.

${\sin}^{−1}(0.96593)≈\dfrac{5\pi}{12}$

Вправа$\PageIndex{1}$

Задано$\cos(0.5)≈0.8776$, запишіть відношення за участю оберненого косинуса.

Відповідь

$\arccos(0.8776)≈0.5$

Пошук точного значення виразів із оберненими функціями синуса, косинуса та тангенса

Тепер, коли ми можемо ідентифікувати зворотні функції, ми навчимося їх оцінювати. Для більшості значень у їхніх областях ми повинні оцінити обернені тригонометричні функції за допомогою калькулятора, інтерполяції з таблиці або за допомогою іншої числової техніки. Так само, як ми робили з оригінальними тригонометричними функціями, ми можемо дати точні значення для обернених функцій, коли ми використовуємо спеціальні кути, зокрема$\dfrac{\pi}{6}$ (30°),$\dfrac{\pi}{4}$ (45°) та$\dfrac{\pi}{3}$ (60°), і їх відображення в інших квадрантах.

Задано «спеціальне» вхідне значення, оцініть обернену тригонометричну функцію.

1. Знайти кут,$x$ для якого вихідна тригонометрична функція має вихід, рівний заданому входу для оберненої тригонометричної функції.
2. Якщо$x$ він не знаходиться в заданому діапазоні зворотного, знайдіть інший кут,$y$ який знаходиться в заданому діапазоні і має ті самі синус, косинус або тангенс$x$, що і, залежно від того, який відповідає заданій оберненій функції.

Приклад$\PageIndex{2}$: Evaluating Inverse Trigonometric Functions for Special Input Values

Оцініть кожне з наступних дій.

1. ${\sin}^{−1}\left(\dfrac{1}{2}\right)$
2. ${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$
3. ${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$
4. ${\tan}^{−1}(1)$

Рішення

1. Оцінка${\sin}^{−1}\left(\dfrac{1}{2}\right)$ така ж, як визначення кута, який мав би значення синуса$\dfrac{1}{2}$. Іншими словами, який кут$x$ задовольнить$\sin(x)=\dfrac{1}{2}$? Є кілька значень, які задовольняли б цю залежність$\dfrac{5\pi}{6}$, такі як$\dfrac{\pi}{6}$ і, але ми знаємо, що нам потрібен кут в інтервалі$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, тому відповідь буде${\sin}^{−1}\left (\dfrac{1}{2}\right)=\dfrac{\pi}{6}$. Пам'ятайте, що зворотна є функцією, тому для кожного входу ми отримаємо рівно один вихід.
2. Щоб оцінити${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)$, ми знаємо, що$\dfrac{5\pi}{4}$ і$\dfrac{7\pi}{4}$ обидва мають значення синуса$-\dfrac{\sqrt{2}}{2}$, але жоден не знаходиться в інтервалі$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. Для цього нам потрібен негативний кут співтермінал з$\dfrac{7\pi}{4}$:${\sin}^{−1}\left(−\dfrac{\sqrt{2}}{2}\right)=−\dfrac{\pi}{4}$.
3. Для оцінки${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)$ шукаємо кут в інтервалі$[ 0,\pi ]$ зі значенням косинуса$-\dfrac{\sqrt{3}}{2}$. Кут, який задовольняє це, є${\cos}^{−1}\left(−\dfrac{\sqrt{3}}{2}\right)=\dfrac{5\pi}{6}$.
4. Оцінюючи${\tan}^{−1}(1)$, шукаємо кут в інтервалі$\left(−\dfrac{\pi}{2},\dfrac{\pi}{2}\right)$ з тангенсом значення$1$. Правильний кут - це${\tan}^{−1}(1)=\dfrac{\pi}{4}$.

Вправа$\PageIndex{2}$

Оцініть кожне з наступних дій.

1. ${\sin}^{−1}(−1)$
2. ${\tan}^{−1}(−1)$
3. ${\cos}^{−1}(−1)$
4. ${\cos}^{−1}\left(\dfrac{1}{2}\right)$

Відповідь на

$-\dfrac{\pi}{2}$

Відповідь б

$-\dfrac{\pi}{4}$

Відповідь c

$\pi$

Відповідь d

$\dfrac{\pi}{3}$

Використання калькулятора для оцінки обернених тригонометричних функцій

Для оцінки обернених тригонометричних функцій, які не передбачають спеціальних кутів, розглянутих раніше, нам буде потрібно скористатися калькулятором або іншим типом техніки. Більшість наукових калькуляторів та програм, що емулюють калькулятори, мають спеціальні клавіші або кнопки для функцій зворотного синуса, косинуса та тангенса. Вони можуть бути позначені, наприклад, SIN-1, ARCSIN або ASIN.

У попередньому розділі ми працювали з тригонометрією на прямокутний трикутник, щоб вирішити для сторін трикутника задану одну сторону і додатковий кут. Використовуючи обернені тригонометричні функції, ми можемо вирішити для кутів прямокутного трикутника задані дві сторони, і ми можемо використовувати калькулятор для пошуку значень до декількох десяткових знаків.

У цих прикладах та вправах відповіді будуть інтерпретовані як кути, і ми будемо використовувати$\theta$ як незалежну змінну. Значення, що відображається на калькуляторі, може бути в градусах або радіанах, тому обов'язково встановіть режим, відповідний додатку.

Приклад$\PageIndex{3}$: Evaluating the Inverse Sine on a Calculator

Оцініть${\sin}^{−1}(0.97)$ за допомогою калькулятора.

Рішення

Оскільки виходом оберненої функції є кут, калькулятор дасть нам значення ступеня, якщо в градусному режимі, і значення радіана, якщо в радіановому режимі. Калькулятори також використовують ті ж обмеження домену на кутах, які ми використовуємо.

У радіановому режимі,${\sin}^{−1}(0.97)≈1.3252$. У градусному режимі,${\sin}^{−1}(0.97)≈75.93°$. Зверніть увагу, що в обчисленні і за його межами ми будемо використовувати радіани майже у всіх випадках.

Вправа$\PageIndex{3}$

Оцініть${\cos}^{−1}(−0.4)$ за допомогою калькулятора.

Відповідь

$1.9823$або$113.578^{\circ}$

Враховуючи дві сторони прямокутного трикутника, як показано на малюнку 8.4.7, знайдіть кут.

Малюнок$\PageIndex{7}$

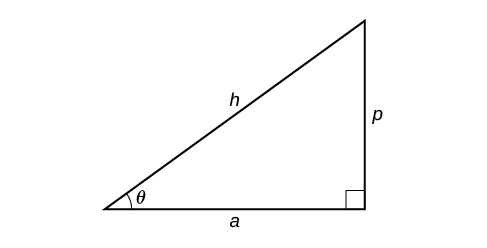
1. Якщо одна задана сторона є гіпотенузою довжини$h$ і задана сторона довжини,$a$ прилегла до потрібного кута, використовуйте рівняння$\theta={\cos}^{−1}\left(\dfrac{a}{h}\right)$.
2. Якщо одна задана сторона є гіпотенузою довжини$h$ і задана сторона довжини,$p$ протилежна потрібному куту, використовуйте рівняння$\theta={\sin}^{−1}\left(\dfrac{p}{h}\right)$.
3. Якщо задані дві ноги (сторони, прилеглі до прямого кута), то використовуйте рівняння$\theta={\tan}^{−1}\left(\dfrac{p}{a}\right)$.

Приклад$\PageIndex{4}$: Applying the Inverse Cosine to a Right Triangle

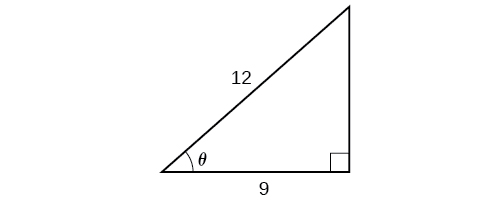
Розв'яжіть трикутник$\PageIndex{8}$ на малюнку для кута$\theta$.

Малюнок$\PageIndex{8}$

Рішення

Оскільки ми знаємо гіпотенузу і сторону, прилеглу до кута, нам має сенс використовувати функцію косинуса.

$$\begin{align*} \cos \theta&= \dfrac{9}{12}\\ \theta&= {\cos}^{-1}\left(\dfrac{9}{12}\right)\qquad \text{Apply definition of the inverse}\\ \theta&\approx 0.7227\qquad \text{or about } 41.4096^{\circ} \text{ Evaluate} \end{align*}$$

Вправа$\PageIndex{4}$

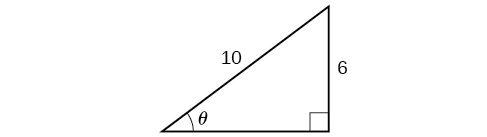
Розв'яжіть трикутник$\PageIndex{9}$ на малюнку для кута$\theta$.

Малюнок$\PageIndex{9}$

Відповідь

${\sin}^{−1}(0.6)=36.87°=0.6435$радіани

Пошук точних значень композитних функцій із оберненими тригонометричними функціями

Бувають випадки, коли нам потрібно скласти тригонометричну функцію з оберненою тригонометричною функцією. У цих випадках ми зазвичай можемо знайти точні значення для отриманих виразів, не вдаючись до калькулятора. Навіть коли вхід до складеної функції є змінною або виразом, ми часто можемо знайти вираз для виведення. Щоб допомогти розібратися в різних випадках, нехай$f(x)$ і$g(x)$ будуть дві різні тригонометричні функції, що належать множині {$\sin(x)$$\cos(x)$,,$\tan(x)$} і нехай$f^{-1}(y)$ і$g^{-1}(y)$ бути їх зворотними.

Оцінка складів форми$f(f^{-1}(y))$ і$f^{-1}(f(x))$

Для будь-якої тригонометричної функції,$f(f^{-1}(y))=y$ для всіх$y$ у належній області для даної функції. Це випливає з визначення зворотного і з того, що діапазон$f$ був визначений як ідентичний області$f^{−1}$. Однак ми повинні бути трохи обережніше з виразами форми$f^{-1}(f(x))$.

СКЛАДИ ТРИГОНОМЕТРИЧНОЇ ФУНКЦІЇ ТА ЇЇ ОБЕРНЕНОЇ

$$\begin{align*} \sin({\sin}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \cos({\cos}^{-1}x)&= x\qquad \text{for } -1\leq x\leq 1\\ \tan({\tan}^{-1}x)&= x\qquad \text{for } -\infty<x<\infty\\ {\sin}^{-1}(\sin x)&= x\qquad \text{only for } -\dfrac{\pi}{2}\leq x\leq \dfrac{\pi}{2}\\ {\cos}^{-1}(\cos x)&= x\qquad \text{only for } 0\leq x\leq \pi\\ {\tan}^{-1}(\tan x)& =x\qquad \text{only for } -\dfrac{\pi}{2}< x< \dfrac{\pi}{2} \end{align*}$$

Q&A

Чи правильно це${\sin}^{−1}(\sin x)=x$?

Ні. Це рівняння є правильним, якщо x належить до обмеженої області$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, але синус визначається для всіх дійсних вхідних значень, а для$x$ поза обмеженим інтервалом рівняння не є правильним, оскільки його зворотне завжди повертає значення в$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$. Аналогічна ситуація для косинусів і тангенсів і їх зворотних. Наприклад,${\sin}^{−1}\left(\sin\left(\dfrac{3\pi}{4}\right)\right)=\dfrac{\pi}{4}$.

Задано вираз форми$f^{-1}(f(\theta))$ where $f(\theta)=\sin \theta$, $\cos \theta$, or $\tan \theta$, evaluate.

1. Якщо$\theta$ знаходиться в обмеженому домені$f$, то$f^{−1}(f(\theta))=\theta$.
2. Якщо ні, то знайти кут$\phi$ в межах обмеженого домену off такий, що$f(\phi)=f(\theta)$. Потім$f^{−1}(f(\theta))=\phi$.

Приклад$\PageIndex{5}$: Using Inverse Trigonometric Functions

Оцініть наступне:

1. ${\sin}^{−1}\left (\sin \left(\dfrac{\pi}{3}\right )\right )$
2. ${\sin}^{−1}\left (\sin \left(\dfrac{2\pi}{3}\right )\right )$
3. ${\cos}^{−1}\left (\cos \left (\dfrac{2\pi}{3}\right )\right )$
4. ${\cos}^{−1}\left (\cos \left (−\dfrac{\pi}{3}\right )\right )$

Рішення

1. $\dfrac{\pi}{3}$знаходиться в$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, так${\sin}^{−1}\left(\sin\left(\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
2. $\dfrac{2\pi}{3}$не в$\left[−\dfrac{\pi}{2},\dfrac{\pi}{2}\right]$, але$sin\left(\dfrac{2\pi}{3}\right)=sin\left(\dfrac{\pi}{3}\right)$, так${\sin}^{−1}\left(\sin\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{\pi}{3}$.
3. $\dfrac{2\pi}{3}$знаходиться в$[ 0,\pi ]$, так${\cos}^{−1}\left(\cos\left(\dfrac{2\pi}{3}\right)\right)=\dfrac{2\pi}{3}$.
4. $-\dfrac{\pi}{3}$не в$[ 0,\pi ]$, а$\cos\left(−\dfrac{\pi}{3}\right)=\cos\left(\dfrac{\pi}{3}\right)$ тому, що косинус - це парна функція. $\dfrac{\pi}{3}$знаходиться в$[ 0,\pi ]$, так${\cos}^{−1}\left(\cos\left(−\dfrac{\pi}{3}\right)\right)=\dfrac{\pi}{3}$.

Вправа$\PageIndex{5}$

Оцініть${\tan}^{−1}\left(\tan\left(\dfrac{\pi}{8}\right)\right)$ і${\tan}^{−1}\left(\tan\left(\dfrac{11\pi}{9}\right)\right)$.

Відповідь

$\dfrac{\pi}{8}$;$\dfrac{2\pi}{9}$

Оцінка складів форми$f^{-1}(g(x))$

Тепер, коли ми можемо скласти тригонометричну функцію з її оберненою, ми можемо дослідити, як оцінити склад тригонометричної функції та зворотну іншу тригонометричну функцію. Почнемо з композицій форми$f^{-1}(g(x))$. Для спеціальних значень$x$, ми можемо точно оцінити внутрішню функцію, а потім зовнішню, обернену функцію. Однак ми можемо знайти більш загальний підхід, розглянувши співвідношення між двома гострими кутами прямокутного трикутника, де один є$\theta$, зробивши інший$\dfrac{\pi}{2}−\theta$ .Розглянемо синус і косинус кожного кута прямокутного трикутника на малюнку$\PageIndex{10}$.

Малюнок$\PageIndex{10}$: Прямокутний трикутник, що ілюструє співвідношення співфункцій

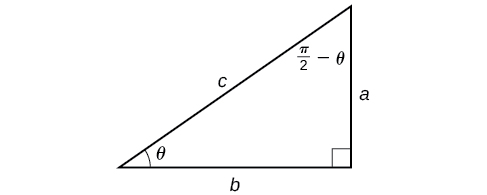
Тому що$\cos \theta=\dfrac{b}{c}=sin\left(\dfrac{\pi}{2}−\theta\right)$, у нас є${\sin}^{−1}(\cos \theta)=\dfrac{\pi}{2}−\theta$ це$0≤\theta≤\pi$. Якщо$\theta$ не в цій області, то нам потрібно знайти інший кут, який має той же косинус, як$\theta$ і належить до обмеженого домену; ми потім віднімаємо цей кут$\dfrac{\pi}{2}$ з.Аналогічно$\sin \theta=\dfrac{a}{c}=\cos\left(\dfrac{\pi}{2}−\theta\right)$, так що${\cos}^{−1}(\sin \theta)=\dfrac{\pi}{2}−\theta$ якщо$−\dfrac{\pi}{2}≤\theta≤\dfrac{\pi}{2}$. Це лише взаємозв'язки функція-співфункція, представлені по-іншому.

Задані функції форми${\sin}^{−1}(\cos x)$ and ${\cos}^{−1}(\sin x)$, evaluate them.

1. Якщо$x$ є в$[ 0,\pi ]$, то${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−x$.
2. Якщо$x$ немає в$[ 0,\pi ]$, то знайдіть інший кут$y$ в$[ 0,\pi ]$ такому, що$\cos y=\cos x$.

   $${\sin}^{−1}(\cos x)=\dfrac{\pi}{2}−y$$

3. Якщо$x$ є в$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, то${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−x$.
4. Якщо$x$ немає в$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$, то знайдіть інший кут$y$ в$\left[ −\dfrac{\pi}{2},\dfrac{\pi}{2} \right]$ такому, що$\sin y=\sin x$.

   $${\cos}^{−1}(\sin x)=\dfrac{\pi}{2}−y$$

Приклад$\PageIndex{6}$: Evaluating the Composition of an Inverse Sine with a Cosine

Оцінити${\sin}^{−1}\left(\cos\left(\dfrac{13\pi}{6}\right)\right)$

1. шляхом безпосередньої оцінки.
2. за способом, описаним раніше.

Рішення

1. Тут ми можемо безпосередньо оцінити внутрішню частину композиції. $$\begin{align*} \cos\left(\dfrac{13\pi}{6}\right)&= \cos\left (\dfrac{\pi}{6}+2\pi\right )\\ &= \cos\left (\dfrac{\pi}{6}\right )\\ &= \dfrac{\sqrt{3}}{2} \end{align*}$$ Тепер ми можемо оцінити зворотну функцію, як ми робили раніше. $${\sin}^{−1}\left (\dfrac{\sqrt{3}}{2}\right )=\dfrac{\pi}{3}$$
2. У нас є$x=\dfrac{13\pi}{6}$$y=\dfrac{\pi}{6}$, і $$\begin{align*} {\sin}^{-1}\left (\cos \left (\dfrac{13\pi}{6} \right ) \right )&= \dfrac{\pi}{2}-\dfrac{\pi}{6}\\ &= \dfrac{\pi}{3} \end{align*}$$

Вправа$\PageIndex{6}$

Оцінити${\cos}^{−1}\left (\sin\left (−\dfrac{11\pi}{4}\right )\right )$.

Відповідь

$\dfrac{3\pi}{4}$

Оцінка складів форми$f(g^{−1}(x))$

Для оцінки композицій виду$f(g^{−1}(x))$, де$f$ і$g$ є будь-якими двома функціями синус, косинус або тангенс і$x$ є будь-яким входом в області$g^{−1}$, ми маємо точні формули, такі як$\sin({\cos}^{−1}x)=\sqrt{1−x^2}$. Коли нам потрібно їх використовувати, ми можемо вивести ці формули, використовуючи тригонометричні відносини між кутами і сторонами прямокутного трикутника разом з використанням відношення Піфагора між довжинами сторін. Ми можемо використовувати піфагорійську ідентичність${\sin}^2 x+{\cos}^2 x=1$, щоб вирішити для одного, коли дано інше. Ми також можемо використовувати обернені тригонометричні функції для пошуку композицій за участю алгебраїчних виразів.

Приклад$\PageIndex{7}$: Evaluating the Composition of a Sine with an Inverse Cosine

Знайдіть точне значення для$\sin\left({\cos}^{−1}\left(\dfrac{4}{5}\right)\right)$.

Рішення

Починаючи з внутрішньої сторони, можна сказати, є якийсь кут такий$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$, що, що означає$\cos \theta=\dfrac{4}{5}$, і ми шукаємо$\sin \theta$. Ми можемо використовувати піфагорійську ідентичність для цього.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use our known value for cosine}\\ {\sin}^2 \theta+{\left (\dfrac{4}{5} \right )}^2&= 1\qquad \text{Solve for sine}\\ {\sin}^2 \theta&= 1-\dfrac{16}{25}\\ \sin \theta&=\pm \dfrac{9}{25}\\ &= \pm \dfrac{3}{5} \end{align*}$$

Оскільки$\theta={\cos}^{−1}\left (\dfrac{4}{5}\right )$ знаходиться в квадранті I,$\sin \theta$ повинен бути позитивним, тому рішення є$35$. Див$\PageIndex{11}$. Малюнок.

Малюнок$\PageIndex{11}$: Прямокутний трикутник ілюструє, що якщо$\cos \theta=\dfrac{4}{5}$, то$\sin \theta=\dfrac{3}{5}$

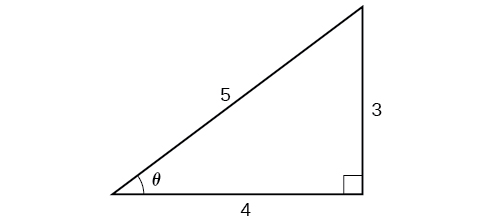
Ми знаємо, що зворотний косинус завжди дає кут на інтервалі$[ 0,\pi ]$, тому ми знаємо, що синус цього кута повинен бути позитивним; отже$\sin \left ({\cos}^{−1}\left (\dfrac{4}{5} \right ) \right )=\sin \theta=\dfrac{3}{5}$.

Вправа$\PageIndex{7}$

Оцінити$\cos \left ({\tan}^{−1} \left (\dfrac{5}{12} \right ) \right )$.

Відповідь

$\frac{12}{13}$

Приклад$\PageIndex{8}$: Evaluating the Composition of a Sine with an Inverse Tangent

Знайдіть точне значення для$\sin\left({\tan}^{−1}\left(\dfrac{7}{4}\right)\right)$.

Рішення

Хоча ми могли б використовувати подібну техніку, як у прикладі$\PageIndex{6}$, ми продемонструємо іншу техніку тут. Зсередини ми знаємо, що є кут такий, що$\tan \theta=\dfrac{7}{4}$. Ми можемо уявити це як протилежну, так і суміжну сторони на прямокутному трикутнику, як показано на малюнку$\PageIndex{12}$.

Малюнок$\PageIndex{12}$: Прямокутний трикутник з двома відомими сторонами

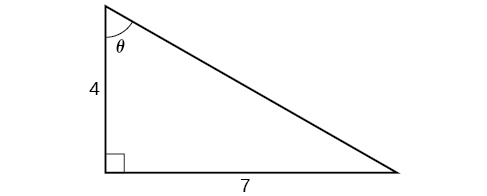
Використовуючи теорему Піфагора, ми можемо знайти гіпотенузу цього трикутника.

\ [\ begin {align*}
4^2+7^2&= {гіпотенуза} ^2\\
гіпотенуза&=\ sqrt {65}
\\ text {Тепер ми можемо оцінити синус кута як протилежну сторону, розділену на гіпотенузу.} \
\ sin\ theta&=\ dfrac {7} {\ sqrt {65}}\
\ text {Це дає нам бажану композицію.} \\ sin
\ ліворуч ({\ tan} ^ {-1}\ ліворуч (\ dfrac {7} {4}\ праворуч)\ праворуч) &=\ sin\ тета\\
&=\ dfrac {7} {\ sqrt {65}}\\
&=\ dfrac {7\ sqrt {65}} {65}
\ end {align*}\]

Вправа$\PageIndex{8}$

Оцінити$\cos\left({\sin}^{−1}\left(\dfrac{7}{9}\right)\right)$.

Відповідь

$\dfrac{4\sqrt{2}}{9}$

Приклад$\PageIndex{9}$: Finding the Cosine of the Inverse Sine of an Algebraic Expression

Знайдіть спрощений вираз для$\cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)$ for$−3≤x≤3$.

Рішення

Ми знаємо, що є$\theta$ такий кут$\sin \theta=\dfrac{x}{3}$.

$$\begin{align*} {\sin}^2 \theta+{\cos}^2 \theta&= 1\qquad \text{Use the Pythagorean Theorem}\\ {\left (\dfrac{x}{3}\right )}^2+{\cos}^2 \theta&= 1\qquad \text{Solve for cosine}\\ {\cos}^2 \theta&= 1-\dfrac{x^2}{9}\\ \cos \theta &= \pm \sqrt{\dfrac{9-x^2}{9}}\\ &= \pm \sqrt{\dfrac{9-x^2}{3}} \end{align*}$$

Оскільки ми знаємо, що зворотний синус повинен дати кут на інтервалі$[ −\dfrac{\pi}{2},\dfrac{\pi}{2} ]$, ми можемо зробити висновок, що косинус цього кута повинен бути позитивним.

$cos\left({\sin}^{−1}\left(\dfrac{x}{3}\right)\right)=\sqrt{\dfrac{9-x^2}{3}}$

Вправа$\PageIndex{9}$

Знайти спрощений вираз для$\sin({\tan}^{−1}(4x))$ for $−\dfrac{1}{4}≤x≤\dfrac{1}{4}$.

Відповідь

$\dfrac{4x}{\sqrt{16x^2+1}}$

Медіа

Отримайте доступ до цього інтернет-ресурсу для додаткової інструкції та практики з оберненими тригонометричними функціями.

• Оцінити вирази за участю обернених тригонометричних функцій

Відвідайте цей веб-сайт для додаткових питань практики від Learningpod.

Ключові поняття

• Зворотна функція - це та, яка «скасовує» іншу функцію. Область оберненої функції - діапазон вихідної функції, а діапазон оберненої функції - область вихідної функції.
• Оскільки тригонометричні функції не є один-на-один у своїх природних областях, обернені тригонометричні функції визначаються для обмежених областей.
• Для будь-якої тригонометричної функції$f(x)$, якщо$x=f^{−1}(y)$, то$f(x)=y$. Однак мається на увазі$f(x)=y$ лише те$x=f^{−1}(y)$,$x$ що знаходиться в обмеженому домені$f$. Див$\PageIndex{1}$. Приклад.
• Спеціальні кути - це виходи обернених тригонометричних функцій для спеціальних вхідних значень; наприклад,$\frac{\pi}{4}={\tan}^{−1}(1)$$\frac{\pi}{6}={\sin}^{−1}(\frac{1}{2})$ і.Див$\PageIndex{2}$. Приклад.
• Калькулятор поверне кут в межах обмеженої області вихідної тригонометричної функції. Див$\PageIndex{3}$. Приклад.
• Зворотні функції дозволяють знайти кут, коли задані дві сторони прямокутного трикутника. Див$\PageIndex{4}$. Приклад.
• У складі функції, якщо внутрішня функція є оберненою тригонометричною функцією, то існують точні вирази; наприклад,$\sin({\cos}^{−1}(x))=\sqrt{1−x^2}$. Див$\PageIndex{5}$. Приклад.
• Якщо внутрішня функція є тригонометричною функцією, то єдино можливі комбінації -${\sin}^{−1}(\cos x)=\frac{\pi}{2}−x$ якщо$0≤x≤\pi$ і${\cos}^{−1}(\sin x)=\frac{\pi}{2}−x$ якщо$−\frac{\pi}{2}≤x≤\frac{\pi}{2}$. Див. Приклад$\PageIndex{6}$ і Приклад$\PageIndex{7}$.
• При оцінці складу тригонометричної функції з оберненою тригонометричною функцією намалюйте опорний трикутник, щоб допомогти у визначенні співвідношення сторін, що представляє вихід тригонометричної функції. Див$\PageIndex{8}$. Приклад.
• При оцінці складу тригонометричної функції з оберненою тригонометричною функцією можна використовувати триг-тотожності, щоб допомогти у визначенні співвідношення сторін. Див$\PageIndex{9}$. Приклад.