3.6: Відносини та функції

Цілі навчання

До кінця цього розділу ви зможете:

• Пошук домену та діапазону зв'язку
• Визначте, чи є відношення функцією
• Знайти значення функції

Перш ніж приступити до роботи, пройдіть цю вікторину про готовність.

1. Оцініть$3x−5$, коли$x=−2$.
   Якщо ви пропустили цю проблему, перегляньте [посилання].
2. Оцініть$2x^2−x−3$, коли$x=a$.
   Якщо ви пропустили цю проблему, перегляньте [посилання].
3. Спростити:$7x−1−4x+5$.
   Якщо ви пропустили цю проблему, перегляньте [посилання].

Пошук домену та діапазону зв'язку

Коли ми йдемо про наше повсякденне життя, у нас є багато елементів даних або величин, які поєднуються з нашими іменами. Наш номер соціального страхування, номер студента, адреса електронної пошти, номер телефону та день народження відповідають нашому імені. Існує взаємозв'язок між нашим ім'ям і кожним з цих пунктів.

Коли ваш професор отримує свій список класів, імена всіх учнів у класі вказані в одному стовпці, а потім номер студентського посвідчення, ймовірно, буде в наступному стовпці. Якщо ми думаємо про відповідність як набір впорядкованих пар, де перший елемент - ім'я студента, а другий елемент - ідентифікаційний номер студента, ми називаємо це відношення.

$$(\text{Student name}, \text{ Student ID #})\nonumber$$

Безліч всіх імен учнів у класі називається доменом відношення, а набір всіх студентських ідентифікаційних номерів в парі з цими учнями - це діапазон відношення.

Існує багато подібних ситуацій, коли одна змінна спарена або збігається з іншою. Набір впорядкованих пар, що записує це відповідність, є співвідношенням.

Визначення: Відносини

Відношення - це будь-який набір впорядкованих пар,$(x,y)$. Всі x -значення в упорядкованих парах разом складають домен. Всі y -значення в упорядкованих парах разом складають діапазон.

Приклад$\PageIndex{1}$

Для відношення${(1,1),(2,4),(3,9),(4,16),(5,25)}$:

1. Знайдіть домен відношення.
2. Знайти діапазон співвідношення.

Відповідь

$$\begin{array} {ll} {} &{ {\{(1,1), (2,4), (3,9), (4,16), (5,25) }\} } \\ {ⓐ\text{ The domain is the set of all x-values of the relation.}} &{ {\{1,2,3,4,5}\} } \\ {ⓑ\text{ The range is the set of all y-values of the relation.}} &{ {\{1,4,9,16,25}\} } \\ \nonumber \end{array}$$

Приклад$\PageIndex{2}$

Для відношення${\{(1,1),(2,8),(3,27),(4,64),(5,125)}\}$:

1. Знайдіть домен відношення.
2. Знайти діапазон співвідношення.

Відповідь на

${\{1,2,3,4,5}\}$

Відповідь б

${\{1,8,27,64,125}\}$

Приклад$\PageIndex{3}$

Для відношення${\{(1,3),(2,6),(3,9),(4,12),(5,15)}\}$:

1. Знайдіть домен відношення.
2. Знайти діапазон співвідношення.

Відповідь на

${\{1,2,3,4,5}\}$

Відповідь б

${\{3,6,9,12,15}\}$

КАРТОГРАФІЯ

Відображення іноді використовується для показу відношення. Стрілками показано сполучення елементів домену з елементами діапазону.

Приклад$\PageIndex{4}$

Використовувати відображення показаного відношення до

1. перерахувати впорядковані пари відношення,
2. знайти домен відношення, і
3. знайти діапазон відношення.

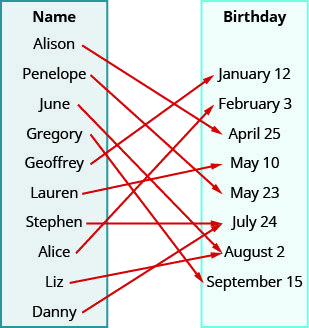
Відповідь

ⓐ Стрілка показує відповідність людини до дня народження. Ми створюємо впорядковані пари з ім'ям людини як значення x і їх день народження як y -значення.

{(Елісон, 25 квітня), (Пенелопа, 23 травня), (Червень, 2 серпня), (Грегорі, 15 вересня), (Джеффрі, 12 січня), (Лорен, 10 травня), (Стівен, 24 липня), (Аліса, 3 лютого), (Ліз, 2 серпня), (Денні, 24 липня)}

ⓑ Домен - це набір всіх x -значень відношення.

{Елісон, Пенелопа, Червень, Грегорі, Джеффрі, Лорен, Стівен, Еліс, Ліз, Денні}

ⓒ Діапазон - це множина всіх y -значень відношення.

{12 січня, 3 лютого, 25 квітня, 10 травня, 23 травня, 24 липня, 2 серпня, 15 вересня}

Приклад$\PageIndex{5}$

Використовувати відображення показаного відношення до

1. перелічити впорядковані пари відношення
2. знайти домен відношення
3. знайти діапазон відношення.

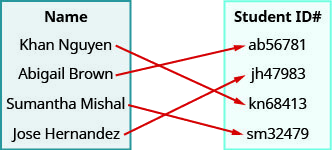
Відповідь

ⓐ (Хань Нгуєн, kn68413), (Ебігейл Браун, ab56781), (Суманта Мішаль, sm32479), (Хосе Херн і Ез, jh47983)

ⓑ {Хань Нгуєн, Ебігейл Браун, Суманта Мішаль, Хосе Херн та Ез}

ⓒ {kn68413, аб56781, см32479, джх47983}

Приклад$\PageIndex{6}$

Використовувати відображення показаного відношення до

1. перелічити впорядковані пари відношення
2. знайти домен відношення
3. знайти діапазон відношення.

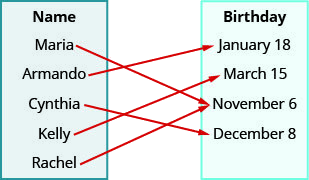
Відповідь

ⓐ (Марія, 6 листопада), (Арм і о, 18 січня), (Синтія, 8 грудня), (Келлі, 15 березня), (Рейчел, 6 листопада)

ⓑ {Марія, Арм і о, Синтія, Келлі, Рейчел}

ⓒ {6 листопада, 18 січня, 8 грудня, 15 березня}

Графік - це ще один спосіб, яким можна представити відношення. Безліч впорядкованих пар всіх покладених точок є співвідношенням. Набір всіх x -координат - це область відношення, а набір усіх y -координат - це діапазон. Зазвичай ми пишемо числа у порядку зростання як для домену, так і для діапазону.

Приклад$\PageIndex{7}$

Використовуйте графік відношення до

1. перелічити впорядковані пари відношення
2. знайти домен відношення
3. знайти діапазон відношення.

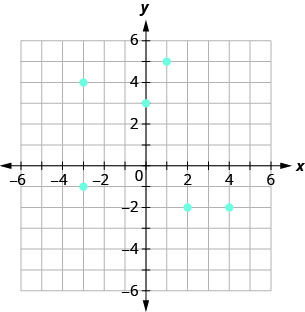
Відповідь

ⓐ Впорядковані пари відношення: $${\{(1,5),(−3,−1),(4,−2),(0,3),(2,−2),(−3,4)}\}.\nonumber$$

ⓑ Домен - це набір всіх x -значень відношення:$\quad {\{−3,0,1,2,4}\}$.

Зверніть увагу, що поки$−3$ повторюється, він вказаний лише один раз.

ⓒ Діапазон - це множина всіх y -значень відношення:$\quad {\{−2,−1,3,4,5}\}$.

Зверніть увагу, що поки$−2$ повторюється, він вказаний лише один раз.

Приклад$\PageIndex{8}$

Використовуйте графік відношення до

1. перелічити впорядковані пари відношення
2. знайти домен відношення
3. знайти діапазон відношення.
4. 

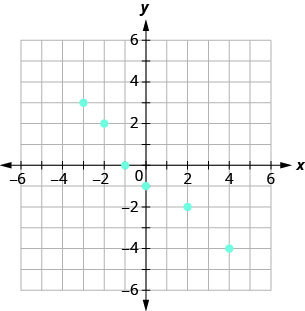
Відповідь

ⓐ$(−3,3),(−2,2),(−1,0),$
$(0,−1),(2,−2),(4,−4)$
ⓑ${\{−3,−2,−1,0,2,4}\}$
ⓒ${\{3,2,0,−1,−2,−4}\}$

Приклад$\PageIndex{9}$

Використовуйте графік відношення до

1. перелічити впорядковані пари відношення
2. знайти домен відношення
3. знайти діапазон відношення.

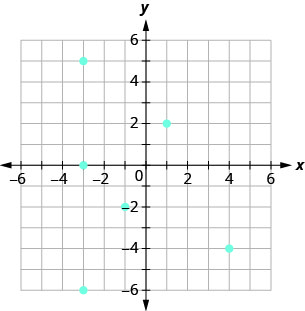
Відповідь

ⓐ$(−3,0),(−3,5),(−3,−6),$
$(−1,−2),(1,2),(4,−4)$
ⓑ${\{−3,−1,1,4}\}$
ⓒ${\{−6,0,5,−2,2,−4}\}$

Визначте, чи є Relation функцією

Особливий тип відношення, званий функцією, широко зустрічається в математиці. Функція - це відношення, яке присвоює кожному елементу в своїй області рівно один елемент в діапазоні. Для кожної впорядкованої пари у співвідношенні кожне x -значення збігається лише з одним y -значенням.

Визначення: Функція

Функція - це відношення, яке присвоює кожному елементу в своїй області рівно один елемент в діапазоні.

Приклад дня народження з Example допомагає нам зрозуміти це визначення. У кожної людини є день народження, але ні у кого немає двох днів народження. Це нормально для двох людей, щоб розділити день народження. ^{Це нормально, що Денні та Стівен поділяють 24 липня як свій день народження, і що червень і Ліз поділяють 2 серпня.} Оскільки у кожної людини рівно один день народження, відношення в Прикладі - це функція.

Співвідношення, показане графіком у прикладі, включає впорядковані пари$(−3,−1)$ і$(−3,4)$. Це нормально в функції? Ні, оскільки це схоже на одну людину, яка має два різних дні народження.

Приклад$\PageIndex{10}$

Використовуйте набір впорядкованих пар, щоб (i) визначити, чи є відношення функцією (ii) знайти область відношення (iii) знайти діапазон відношення.

1. ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$
2. ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

Відповідь

ⓐ${\{(−3,27),(−2,8),(−1,1),(0,0),(1,1),(2,8),(3,27)}\}$

(i) Кожне значення x відповідає лише одному y -значенню. Таким чином, це відношення є функцією.

(ii) Домен - це набір всіх x -значень у відношенні.
Домен:${\{−3,−2,−1,0,1,2,3}\}$.

(iii) Діапазон - це набір усіх y -значень у відношенні. Зверніть увагу, що ми не перераховуємо значення діапазону двічі.
Асортимент становить:${\{27,8,1,0}\}$.

ⓑ${\{(9,−3),(4,−2),(1,−1),(0,0),(1,1),(4,2),(9,3)}\}$

(i) Значення x 9 збігається з двома y -значеннями, як 3, так і$−3$. Так що це відношення не є функцією.

(ii) Домен - це набір всіх x -значень у відношенні. Зверніть увагу, що ми не перераховуємо значення домену двічі.
Домен:${\{0,1,2,4,9}\}$.

(iii) Діапазон - це набір усіх y -значень у відношенні.
Асортимент становить:${\{−3,−2,−1,0,1,2,3}\}$.

Приклад$\PageIndex{11}$

Використовуйте набір впорядкованих пар, щоб (i) визначити, чи є відношення функцією (ii) знайти область відношення (iii) знайти діапазон функції.

1. ${\{(−3,−6),(−2,−4),(−1,−2),(0,0),(1,2),(2,4),(3,6)}\}$
2. ${\{(8,−4),(4,−2),(2,−1),(0,0),(2,1),(4,2),(8,4)}\}$

Відповідь

ⓐ Так;${\{−3,−2,−1,0,1,2,3}\}$;
${\{−6,−4,−2,0,2,4,6}\}$
ⓑ Ні;;${\{0,2,4,8}\}$;
${\{−4,−2,−1,0,1,2,4}\}$

Приклад$\PageIndex{12}$

Використовуйте набір впорядкованих пар, щоб (i) визначити, чи є відношення функцією (ii) знайти область відношення (iii) знайти діапазон відношення.

1. ${\{(27,−3),(8,−2),(1,−1),(0,0),(1,1),(8,2),(27,3)}\}$
2. ${\{(7,−3),(−5,−4),(8,−0),(0,0),(−6,4),(−2,2),(−1,3)}\}$

Відповідь

ⓐ Ні;${\{0,1,8,27}\}$;
${\{−3,−2,−1,0,2,2,3}\}$
ⓑ Так;${\{7,−5,8,0,−6,−2,−1}\}$;
${\{−3,−4,0,4,2,3}\}$

Приклад$\PageIndex{13}$

Скористайтеся відображенням для

1. визначити, чи є відношення функцією
2. знайти домен відношення
3. знайти діапазон відношення.

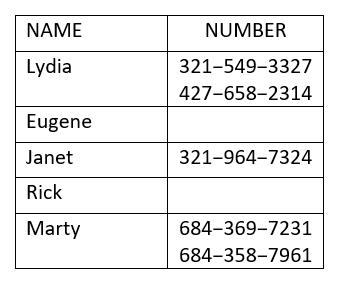
Відповідь

ⓐ І Лідія, і Марті мають два телефонні номери. Таким чином, кожен х -значення не збігається тільки з одним y -значенням. Так що це відношення не є функцією.

ⓑ Домен - це набір всіх x -значень у співвідношенні. Домен: {Лідія, Євген, Джанет, Рік, Марті}

ⓒ Діапазон - це набір всіх y -значень у відношенні. Асортимент - це:

${\{321-549-3327, 427-658-2314, 321-964-7324, 684-358-7961, 684-369-7231, 798-367-8541}\}$

Приклад$\PageIndex{14}$

Використовуйте відображення, щоб ⓐ визначити, чи є відношення функцією ⓑ знайти область відношення ⓒ знайти діапазон відношення.

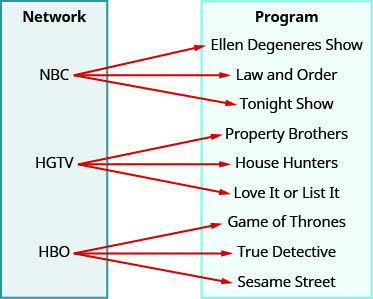
Відповідь

ⓐ no ⓑ {NBC, HGTV, HBO} ⓒ {Шоу Еллен Дедженерес, Закон і порядок, Сьогоднішнє шоу, Брати власності, Мисливці за будинками, Люби це або перерахуй його, Гра престолів, Справжній детектив, Вулиця Сезам}

Приклад$\PageIndex{15}$

Скористайтеся відображенням для

1. визначити, чи є відношення функцією
2. знайти домен відношення
3. знайти діапазон відношення.

 

Відповідь

ⓐ Ні ⓑ {Ніл, Кристал, Кельвін, Джордж, Кріста, Майк} ⓒ {123-567-4839 робота, 231-378-5941 клітина, 743-469-9731 клітина, 567-534-2970 робота, 684-369-7231 клітина, 798-367-8541 клітина, 639-847-6971 клітина}

В алгебрі найчастіше функції будуть представлені рівнянням. Найпростіше побачити, чи є рівняння функцією, коли вона вирішується для y. Якщо кожне значення x призводить лише до одного значення y, тоді рівняння визначає функцію.

Приклад$\PageIndex{16}$

Визначте, чи є кожне рівняння функцією.

1. $2x+y=7$
2. $y=x^2+1$
3. $x+y^2=3$

Відповідь

ⓐ$2x+y=7$

Для кожного значення x множимо його на,$−2$ а потім додаємо 7, щоб отримати y -значення

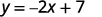
Наприклад, якщо$x=3$: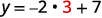

У нас це коли$x=3$, тоді$y=1$. Це буде працювати аналогічно для будь-якого значення x. Оскільки кожне значення x, відповідає лише одному значенню y, рівняння визначає функцію.

ⓑ$y=x^2+1$

Для кожного значення x ми квадратимо його, а потім додаємо 1, щоб отримати y -значення.

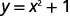
Наприклад, якщо$x=2$:

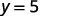
У нас це коли$x=2$, тоді$y=5$. Це буде працювати аналогічно для будь-якого значення x. Оскільки кожне значення x, відповідає лише одному значенню y, рівняння визначає функцію.

ⓒ

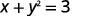
Виділити термін y.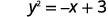
Давайте підставимо$x=2$.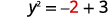
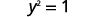
Це дає нам два значення для y.	$y=1\space y=−1$

Ми показали, що коли$x=2$, то$y=1$ і$y=−1$. Це буде працювати аналогічно для будь-якого значення x. Оскільки кожне значення x не відповідає лише одному значенню y, рівняння не визначає функцію.

Приклад$\PageIndex{17}$

Визначте, чи є кожне рівняння функцією.

1. $4x+y=−3$
2. $x+y^2=1$
3. $y−x^2=2$

Відповідь

ⓐ так ⓑ ні ⓒ так

Приклад$\PageIndex{18}$

Визначте, чи є кожне рівняння функцією.

1. $x+y^2=4$
2. $y=x^2−7$
3. $y=5x−4$

Відповідь

ⓐ ні ⓑ так ⓒ так

Знайти значення функції

Дуже зручно називати функцію і найчастіше ми називаємо її f, g, h, F, G або H. У будь-якій функції для кожного x -значення з домену отримуємо відповідне y -значення в діапазоні. Для функції$f$ запишемо це значення діапазону$y$ як$f(x)$. Це називається позначенням функції і$f$ зчитується$x$ або значення$f$ at$x$. У цьому випадку дужки не вказують на множення.

Визначення: Функція позначення

Для функції$y=f(x)$

$$\begin{array} {l} {f\text{ is the name of the function}} \\{x \text{ is the domain value}} \\ {f(x) \text{ is the range value } y \text{ corresponding to the value } x} \\ \nonumber \end{array}$$

Ми читаємо$f(x)$ як$f$$x$ або значення$f$ at$x$.

Ми називаємо x незалежною змінною, оскільки це може бути будь-яке значення в домені. Ми називаємо y залежну змінну, оскільки її значення залежить від x.

НЕЗАЛЕЖНІ ТА ЗАЛЕЖНІ ЗМІННІ

Для функції$y=f(x)$,

$$\begin{array} {l} {x \text{ is the independent variable as it can be any value in the domain}} \\ {y \text{ the dependent variable as its value depends on } x} \\ \nonumber \end{array}$$

Так само, як коли ви вперше зіткнулися зі змінною x, позначення функції може бути досить тривожним. Це здається дивним, тому що воно нове. Ви будете почувати себе більш комфортно з позначенням під час його використання.

Давайте розглянемо рівняння$y=4x−5$. Щоб знайти значення y$x=2$, коли, ми знаємо$x=2$ підставити в рівняння, а потім спростити.

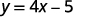Нехай x = 2.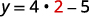

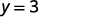Значення функції at$x=2$ дорівнює 3.

Ми робимо те ж саме, використовуючи позначення функції, рівняння$y=4x−5$ можна записати як$f(x)=4x−5$. Щоб знайти значення коли$x=2$, пишемо:

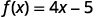Нехай x = 2.

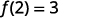Значення функції at$x=2$ дорівнює 3.

Цей процес знаходження значення$f(x)$ для заданого значення x називається оцінкою функції.

Приклад$\PageIndex{19}$

Для функції$f(x)=2x^2+3x−1$ оцініть функцію.

1. $f(3)$
2. $f(−2)$
3. $f(a)$

Відповідь

ⓐ

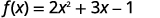
Для оцінки$f(3)$ підставляємо 3 на x.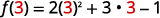
Спростити.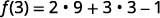

ⓑ

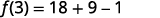
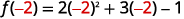
Спростити.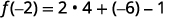

ⓒ

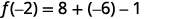
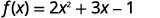
Щоб оцінити f (a), f (a), підставити a на x.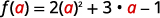
Спростити.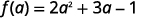

Приклад$\PageIndex{20}$

Для функції$f(x)=3x^2−2x+1$ оцініть функцію.

1. $f(3)$
2. $f(−1)$
3. $f(t)$

Відповідь

ⓐ$f(3)=22$ ⓑ$f(−1)=6$ ⓒ$f(t)=3t^2−2t−1$

Приклад$\PageIndex{21}$

Для функції$f(x)=2x^2+4x−3$ оцініть функцію.

1. $f(2)$
2. $f(−3)$
3. $f(h)$

Відповідь

ⓐ$(2)=13$ ⓑ$f(−3)=3$
ⓒ$f(h)=2h2+4h−3$

В останньому прикладі ми знайшли$f(x)$ постійне значення x. У наступному прикладі нас просять знайти$g(x)$ зі значеннями x, які є змінними. Ми все ще дотримуємося тієї ж процедури і підставляємо змінні в для x.

Приклад$\PageIndex{22}$

Для функції$g(x)=3x−5$ оцініть функцію.

1. $g(h^2)$
2. $g(x+2)$
3. $g(x)+g(2)$

Відповідь

ⓐ

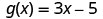
Для оцінки$g(h^2)$$h^2$ підставляємо x.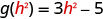

ⓑ

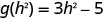
Для оцінки$g(x+2)$$x+2$ підставляємо x.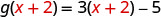
Спростити.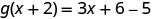

ⓒ

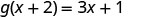
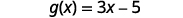
Щоб оцінити$g(x)+g(2)$, спочатку знайдіть$g(2)$.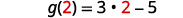
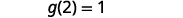
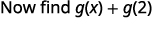
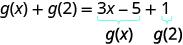
Спростити.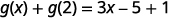

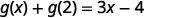
Зверніть увагу на різницю між частиною ⓑ і ⓒ. Отримуємо$g(x+2)=3x+1$ і$g(x)+g(2)=3x−4$. Таким чином, ми бачимо, що$g(x+2)\neq g(x)+g(2)$.

Приклад$\PageIndex{23}$

Для функції$g(x)=4x−7$ оцініть функцію.

1. $g(m^2)$
2. $g(x−3)$
3. $g(x)−g(3)$

Відповідь

ⓐ$4m^2−7$ ⓑ$4x−19$
ⓒ$x−12$

Приклад$\PageIndex{24}$

Для функції$h(x)=2x+1$ оцініть функцію.

1. $h(k^2)$
2. $h(x+1)$
3. $h(x)+h(1)$

Відповідь

ⓐ$2k^2+1$ ⓑ$2x+3$
ⓒ$2x+4$

Багато повсякденних ситуацій можна змоделювати за допомогою функцій.

Приклад$\PageIndex{25}$

Кількість непрочитаних електронних листів в акаунті Сільвії становить 75. Ця кількість зростає на 10 непрочитаних листів на день. Функція$N(t)=75+10t$ представляє зв'язок між кількістю електронних листів, N, і часом, t, виміряним у днях.

1. Визначте незалежну і залежну змінну.
2. Знайти$N(5)$. Поясніть, що означає цей результат.

Відповідь

ⓐ Кількість непрочитаних листів - це функція кількості днів. Кількість непрочитаних листів, N, залежить від кількості днів, т. Отже, змінна N, є залежною змінною, а змінна tt - незалежною змінною.

ⓑ Знайти$N(5)$. Поясніть, що означає цей результат.

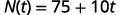
Замінюємо в t=5.t=5.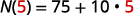
Спростити.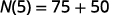

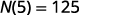
Оскільки 5 - це кількість днів$N(5)$, це кількість непрочитаних листів через 5 днів. Через 5 днів в акаунті залишається 125 непрочитаних листів.

Приклад$\PageIndex{26}$

Кількість непрочитаних листів в акаунті Брайана - 100. Ця кількість зростає на 15 непрочитаних листів на день. Функція$N(t)=100+15t$ представляє зв'язок між кількістю електронних листів, N, і часом, t, виміряним у днях.

1. Визначте незалежну і залежну змінну.
2. Знайти$N(7)]$. Поясніть, що означає цей результат.

Відповідь

ⓐ т IND; N DEP ⓑ 205; кількість непрочитаних листів в обліковому записі Брайана на сьомий день.

Приклад$\PageIndex{27}$

Кількість непрочитаних листів в акаунті Ентоні становить 110. Ця кількість зростає на 25 непрочитаних листів на день. Функція$N(t)=110+25t$ представляє зв'язок між кількістю електронних листів, N, і часом, t, виміряним у днях.

1. Визначте незалежну і залежну змінну.
2. Знайти$N(14)$. Поясніть, що означає цей результат.

Відповідь

ⓐ т IND; N DEP ⓑ 460; кількість непрочитаних листів в акаунті Ентоні на чотирнадцятий день

Отримайте доступ до цього інтернет-ресурсу для додаткових інструкцій та практики з стосунками та функціями.

• Вступ до функцій

Ключові концепції

• Позначення функції: Для функції$y=f(x)$
  • f - назва функції
  • x - значення домену
  • $f(x)$це значення діапазону y, відповідне значенню x
    Ми читаємо$f(x)$ як f x або значення f при x.
• Незалежні та залежні змінні: Для функції$y=f(x)$,
  • x є незалежною змінною, оскільки це може бути будь-яке значення в домені
  • y - залежна змінна, оскільки її значення залежить від x

Глосарій

домен відношення

Домен відношення - це всі x -значення в упорядкованих парах відношення.

функція

Функція - це відношення, яке присвоює кожному елементу в своїй області рівно один елемент в діапазоні.

картографування

Відображення іноді використовується для показу відношення. Стрілками показано сполучення елементів домену з елементами діапазону.

діапазон відношення

Діапазон відношення - це всі y- значення в упорядкованих парах відношення.

відношення

Відношення - це будь-яка сукупність впорядкованих пар, (x, y). (х, у). Всі x -значення в упорядкованих парах разом складають домен. Всі y -значення в упорядкованих парах разом складають діапазон.