3.3: Ставки та нахил

Last updated
Save as PDF

Page ID: 58140

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$

Відкриємо цей розділ із застосуванням поняття ставки.

Незалежний проти залежних

Традиційно розміщувати незалежну змінну на горизонтальній осі, а залежну змінну - на вертикальній осі.

Приклад$\PageIndex{1}$

Об'єкт скидається з відпочинку, потім починає набирати швидкість з постійною швидкістю$10$ метрів в секунду кожну секунду ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$або$10\mathrm{m} / \mathrm{s}^{2}$). Намалюйте графік швидкості об'єкта в порівнянні з часом.

Рішення

В даному прикладі швидкість руху об'єкта залежить від часу. Це робить швидкість залежною змінною, а час незалежною змінною.

Дотримуючись цієї орієнтири, розміщуємо час на горизонтальній осі і швидкість на вертикальній осі. На малюнку зверніть увагу$\PageIndex{1}$, що ми позначили кожну вісь залежними та незалежними змінними ($v$і$t$), і ми включили одиниці ($\mathrm{m} / \mathrm{s}$і$\mathrm{s}$) в наші мітки. Далі нам потрібно масштабувати кожну вісь. Визначаючи шкалу для кожної осі, майте на увазі дві думки:

Підберіть масштаб, який дозволяє зручно будувати графіки заданих даних.
Виберіть масштаб, який дозволить всім зазначеним даними поміститися на графіку.

У цьому прикладі ми хочемо масштаб, який дозволяє зручно показати, що швидкість збільшується зі швидкістю$10$ метрів в секунду ($10\mathrm{m} / \mathrm{s}$) кожну секунду ($\mathrm{m} / \mathrm{s}$). Один з можливих підходів - зробити кожну позначку галочки на горизонтальній осі рівною$1 \mathrm{s}$ і кожну позначку галочки на вертикальній осі рівною$10\mathrm{m} / \mathrm{s}$.

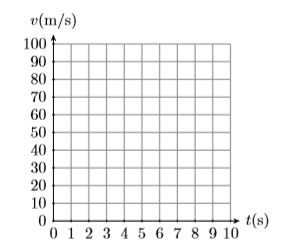
рис. 3.3.1.png — Малюнок$\PageIndex{1}$ : Позначте та масштабуйте кожну вісь. Включити одиниці з мітками.

Далі, за часом$t=0 \mathrm{s}$, швидкість є$v=0 \mathrm{m} / \mathrm{s}$. Це точка,$(t, v)=(0,0)$ нанесена на рис$\PageIndex{2}$. По-друге, швидкість, з якою збільшується швидкість, дорівнює ($10\mathrm{m} / \mathrm{s}$) в секунду. Це означає, що кожен раз, коли ви рухаєтеся$1$ секундою вправо, швидкість збільшується на ($10\mathrm{m} / \mathrm{s}$).

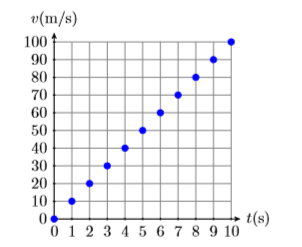
рис. 3.3.2.png — Малюнок$\PageIndex{2}$ : Почніть з$(0,0)$, потім безперервно рухайтеся$1$ вправо і$10$ вгору.

На малюнку$\PageIndex{2}$ почніть з$(0,0)$, потім$1 \mathrm{s}$ рухайтеся вправо і ($10\mathrm{m} / \mathrm{s}$) вгору. Це ставить вас в точку$(1,10)$, яка говорить про те, що через$1$ секунду швидкість частки дорівнює ($10\mathrm{m} / \mathrm{s}$). Продовжуйте таким чином, безперервно$1 \mathrm{s}$ рухаючись вправо і ($10\mathrm{m} / \mathrm{s}$) вгору. Це дає послідовність точок, показану на малюнку$\PageIndex{2}$. Зверніть увагу, що ця постійна швидкість$10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$ змушує графік швидкості в порівнянні з часом бути лінією, як зображено на малюнку$\PageIndex{3}$.

альт — Малюнок$\PageIndex{3}$ : Постійна швидкість змушує графік бути лінією.

рис. 3.3.3.png — Малюнок$\PageIndex{3}$ : Постійна швидкість змушує графік бути лінією.

Вправа$\PageIndex{1}$

Починаючи з відпочинку, автомобіль набирає швидкість з постійною швидкістю$5$ миль на годину кожну секунду (5$(\mathrm{mi} / \mathrm{hr}) / \mathrm{s}$). Намалюйте графік швидкості об'єкта в порівнянні з часом.

Відповідь: $Вправа 3.3.1.png$

Вимірювання зміни змінної

Щоб обчислити зміну деякої кількості, беремо різницю. Наприклад, припустимо, що температура вранці є$40^{\circ} \mathrm{F}$, то вдень температура вимірюється$60^{\circ} \mathrm{F}$ (F позначає температуру Фаренгейта). Тоді зміна температури знаходять, взявши різницю.

\[\begin{aligned} \text { Change in temperature } &=\text { Afternoon temperature - Morning temperature } \\ &=60^{\circ} \mathrm{F}-40^{\circ} \mathrm{F} \\ &=20^{\circ} \mathrm{F} \end{aligned} \nonumber\]

Тому спостерігалося двадцятиградусне підвищення температури з ранку до полудня.

Тепер припустимо, що вечірня температура вимірюється$50^{\circ} \mathrm{F}$. Щоб розрахувати зміну температури з полудня до вечора, знову віднімаємо.

\[\begin{aligned} \text { Change in temperature } &=\text { Evening temperature - Afternoon temperature } \\ &=50^{\circ} \mathrm{F}-60^{\circ} \mathrm{F} \\ &=-10^{\circ} \mathrm{F} \end{aligned} \nonumber \]

Відзначалося зниження температури на десять градусів з дня до вечора.

Обчислення зміни кількості

Щоб обчислити зміну кількості, відніміть попереднє вимірювання з пізнішого вимірювання.

Нехай$T$ представляють температуру. Математики люблять використовувати символіку$\Delta T$ для представлення зміни температури. Для зміни температури з ранку до полудня ми б написали$\Delta T=20^{\circ} \mathrm{F}$. Для змін у другій половині дня на вечір ми б написали$\Delta T=-10^{\circ} \mathrm{F}$.

Математики та вчені часто використовують грецький алфавіт, перші кілька літер якого:

$\begin{array}{ll}{\alpha, \beta, \gamma, \delta, \ldots} & {\text { (Greek alphabet, lower case) }} \\ {A, B, \Gamma, \Delta, \ldots} & {\text { (Greek alphabet, upper case) }} \\ {a, b, c, d, \ldots} & {\text { (English alphabet) }}\end{array}$

Таким чином, грецька буква$\Delta T$, верхня форма регістру$\delta$, корелює з літерою 'd' в англійському алфавіті. Чому математики зробили такий вибір букви, щоб представляти зміну кількості? Тому що, щоб знайти зміну кількості, ми беремо різницю, а слово «різниця» починається з літери 'd.' Таким чином,$\Delta T$ також вимовляється «різниця в Т.»

Важливі вимови

Два способи вимови символіки ΔT.

$\Delta T$вимовляється «зміна Т.»
$\Delta T$також вимовляється «різниця в Т.»

Нахил як швидкість

Ось визначення нахилу лінії.

Ухил

Нахил лінії - це швидкість, з якою залежна змінна змінюється відносно незалежної змінної. Наприклад, якщо залежна змінна є,$y$ а незалежна змінна є$x$, то нахил лінії дорівнює:

Ухил$=\dfrac{\Delta y}{\Delta x}$

Приклад$\PageIndex{2}$

У прикладі об'єкт$\PageIndex{1}$, звільнений від спокою, побачив, що його швидкість збільшувалася з постійною швидкістю$10$ метрів в секунду ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$або$10\mathrm{m} / \mathrm{s}^{2}$). Ця постійна швидкість змусила графік швидкості проти часу бути лінією, показаною на малюнку$\PageIndex{3}$. Обчисліть ухил цієї лінії.

Рішення

Почніть з вибору двох точок$P(2,20)$ і$Q(8,80)$ на лінії, як показано на малюнку$\PageIndex{4}$. Щоб знайти нахил цієї лінії, визначення вимагає знайти швидкість, з якою залежна змінна$v$ змінюється щодо незалежної змінної$t$. Тобто нахил - це зміна$v$ розділеного на зміну в$t$. В символах:

Ухил$=\dfrac{\Delta v}{\Delta t}$

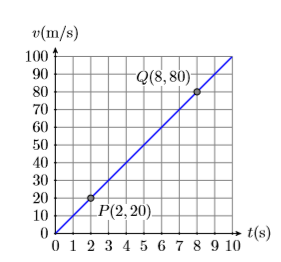
рис. 3.3.4.png — Малюнок$\PageIndex{4}$: Виберіть дві точки, щоб обчислити нахил.

Тепер, коли ми рухаємося від точки$P(2,20)$ до точки$Q(8,80)$, швидкість змінюється від$20\mathrm{m} / \mathrm{s}$ до$80\mathrm{m} / \mathrm{s}$. Таким чином, зміна швидкості становить:

$\begin{aligned} \Delta v &=80 \mathrm{m} / \mathrm{s}-20 \mathrm{m} / \mathrm{s} \\ &=60 \mathrm{m} / \mathrm{s} \end{aligned}$

Аналогічно, коли ми рухаємося від точки Р (2,20) до точки Q (8,80), час змінюється від 2 секунд до 8 секунд. Таким чином, зміна часу - це:

$\begin{aligned} \Delta t &=8 \mathrm{s}-2 \mathrm{s} \\ &=6 \mathrm{s} \end{aligned}$

Тепер, коли у нас є як зміна залежних, так і незалежних змінних, ми можемо обчислити нахил.

$\begin{aligned} \text { Slope } &=\frac{\Delta v}{\Delta t} \\ &=\frac{60 \mathrm{m} / \mathrm{s}}{6 \mathrm{s}} \\ &=10 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{s}} \end{aligned}$

Тому ухил лінії становить$10$ метри в секунду в секунду ($10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$або$10\mathrm{m} / \mathrm{s}^{2}$).

Нахил лінії не залежить від вибраних вами точок. Спробуємо розрахунок ухилу ще раз, використовуючи дві різні точки і більш компактне уявлення необхідних розрахунків. Виберіть точки$P(3,30)$ і$Q(7,70)$, як показано на малюнку$\PageIndex{5}$. Використовуючи ці дві нові точки, нахил - це швидкість, з якою залежна змінна$v$ змінюється щодо незалежної змінної$t$.

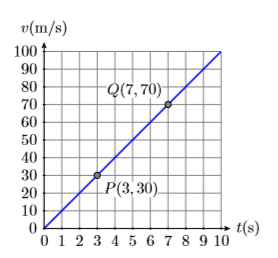
рис. 3.3.5.png — Малюнок$\PageIndex{5}$ : Нахил не залежить від точок, які ми вибираємо на лінії.

$\begin{aligned} \text { Slope } &=\frac{\Delta v}{\Delta t} \\ &=\frac{70 \mathrm{m} / \mathrm{s}-30 \mathrm{m} / \mathrm{s}}{7 \mathrm{s}-3 \mathrm{s}} \\ &=\frac{40 \mathrm{m} / \mathrm{s}}{4 \mathrm{s}} \\ &=10 \frac{\mathrm{m} / \mathrm{s}}{\mathrm{s}} \end{aligned}$

Знову ж таки, нахил лінії є$10(\mathrm{m} / \mathrm{s}) / \mathrm{s}$.

Вправа$\PageIndex{2}$

Починаючи з відпочинку, автомобіль набирає швидкість з постійною швидкістю 5 миль на годину кожну секунду (5 (миль/год) /с). Постійна швидкість змушує графік швидкості об'єкта в порівнянні з часом бути лінією. Обчисліть ухил цієї лінії.

Відповідь: $5(\mathrm{mi} / \mathrm{hr}) / \mathrm{s}$

Приклад$\PageIndex{2}$ вказує на наступний факт.

Ухил не залежить від обраних точок

Неважливо, які дві точки ви виберете на лінії, щоб обчислити її нахил.

Наступний приклад демонструє, що нахил також не залежить від порядку віднімання.

Приклад$\PageIndex{3}$

Обчислити нахил лінії, що проходить через точки$P(−1,−2)$ і$Q(3,3)$.

Рішення

Спочатку намалюйте лінію, що проходить через точки P (−1, −2) і Q (3,3) (див.$\PageIndex{6}$ Рис.

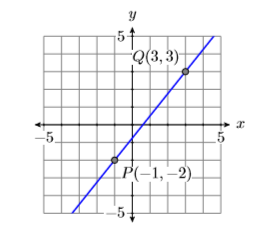
рис. 3.3.6.png — Малюнок$\PageIndex{6}$ : Обчислення нахилу лінії, що проходить через точки$P(−1,−2)$ і$Q(3,3)$.

Щоб обчислити нахил лінії через точки$P(−1,−2)$ і$Q(3,3)$, ми повинні обчислити зміну як незалежних, так і залежних змінних. Ми зробимо це двома різними способами.

Попередження!

Якщо ви не послідовні в напрямку віднімання, ви не отримаєте правильної відповіді для нахилу.

Наприклад:\[\dfrac{3-(-2)}{-1-3}=-\dfrac{5}{4} \nonumber \]

У цьому випадку ми віднімали$y$ -координату точки$P(−1,−2)$ з$y$ -координати точки$Q(3,3)$, але потім ми змінили коней в середині потоку, віднімаючи$x$ -координату точки$Q(3,3)$ з$x$ -координати точки$P(−1,−2)$. Відзначимо, що отримуємо негативний від правильної відповіді.

Спосіб 1

Відніміть координати точки$P(−1,−2)$ з координат точки$Q(3,3)$.

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-2)}{3-(-1)} \\ &=\dfrac{5}{4} \end{aligned} \nonumber \]

Спосіб 2

Відніміть координати точки$Q(3,3)$ з координат точки$P(−1,−2)$.

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-2-3}{-1-3} \\ &=\dfrac{-5}{-4} \\ &=\dfrac{5}{4} \end{aligned} \nonumber \]

Зверніть увагу, що незалежно від напрямку віднімання нахил є$5/4$.

Вправа$\PageIndex{3}$

Обчислити нахил прямої, що проходить через точки P (−3,1) і Q (2,4).

Відповідь: $3/5$

Приклад$\PageIndex{3}$ демонструє наступний факт.

Напрямок віднімання значення не має

При розрахунку нахилу лінії через дві точки$P$ і$Q$, неважливо, в який бік ви віднімаєте, за умови, що ви залишаєтеся послідовними у виборі напрямку.

Крутизна лінії

Нам потрібно вивчити, чи відповідає наше визначення схилу певним очікуванням.

Ухил і крутизна лінії

Нахил лінії - це число, яке говорить нам про те, наскільки крута лінія.

Якщо нахил - це число, яке вимірює крутизну лінії, то можна було б очікувати, що більш крута лінія матиме більший нахил.

Приклад$\PageIndex{4}$

Графік дві лінії, перша проходить через точки$P(−3,−2)$ $Q(3,2)$ і друга через точки$R(−1,−3)$ і$S(1,3)$. Обчисліть нахил кожної лінії і порівняйте результати.

Рішення

Показані графіки двох ліній через задані точки, перша на малюнку$\PageIndex{7}$ і друга на рис$\PageIndex{8}$. Зверніть увагу, що лінія на малюнку$\PageIndex{7}$ менш крута, ніж лінія на малюнку$\PageIndex{8}$.

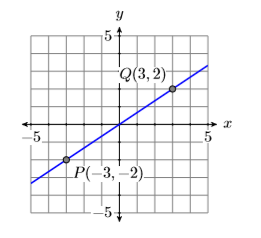
рис. 3.3.7.png — Малюнок$\PageIndex{7}$: Ця лінія менш крута, ніж лінія праворуч. **Малюнок$\PageIndex{8}$:** Ця лінія крутіша, ніж лінія зліва.

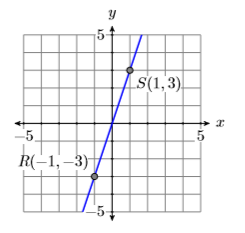
рис. 3.3.8.png — Малюнок$\PageIndex{7}$: Ця лінія менш крута, ніж лінія праворуч. **Малюнок$\PageIndex{8}$:** Ця лінія крутіша, ніж лінія зліва.

Пам'ятайте, нахил лінії - це швидкість, з якою змінюється залежна змінна щодо незалежної змінної. У обох Figure$\PageIndex{7}$ і Figure залежна змінна є$\PageIndex{8}$,$y$ а незалежна змінна є$x$.

Відніміть координати точки$P(−3,−2)$ з координат точки$Q(3,2)$.

\[\begin{aligned} \text { Slope of first line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{2-(-2)}{3-(-3)} \\ &=\dfrac{4}{6} \\ &=\dfrac{2}{3} \end{aligned} \nonumber \]

Відніміть координати точки$R(−1,−3)$ з точки$S(1,3)$.

\[\begin{aligned} \text { Slope of second line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-3)}{1-(-1)} \\ &=\dfrac{6}{2} \\ &=3 \end{aligned} \nonumber \]

Зверніть увагу, що обидві лінії йдуть в гору, і обидві мають позитивні нахили. Також врахуйте, що ухил другої лінії більше, ніж нахил першої лінії. Це узгоджується з тим, що друга лінія крутіше першої.

Вправа$\PageIndex{4}$

Обчислити нахил лінії, що проходить через точки$P(−2,−3)$ and $Q(2,5)$. Then compute the slope of the line passing through the points $R(−2,−1)$ and $S(5,3)$, and compare the two slopes. Which line is steeper?

Відповідь: Перша лінія має нахил$2$, а друга - ухил$4/7$. Перша лінія крутіше.

У прикладі обидві лінії похилі вгору$\PageIndex{4}$, і обидві мали позитивні схили, тим крутіша з двох ліній, що мають більший нахил. Давайте тепер подивимося на дві лінії, які нахиляються вниз.

Приклад$\PageIndex{5}$

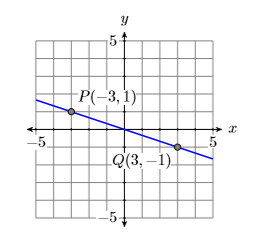
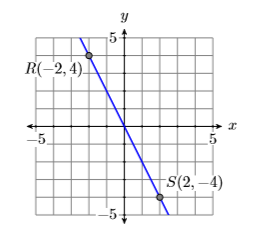
Графік дві лінії, перша проходить через точки$P(−3,1)$$Q(3,−1)$ і друга через точки$R(−2,4)$ і$S(2,−4)$. Обчисліть нахил кожної лінії і порівняйте результати.

Рішення

Показані графіки двох ліній через задані точки, перша на малюнку$\PageIndex{9}$ і друга на рис$\PageIndex{10}$. Зверніть увагу, що лінія на малюнку$\PageIndex{9}$ йде вниз менш швидко, ніж лінія на малюнку$\PageIndex{10}$. Пам'ятайте, нахил лінії - це швидкість, з якою змінюється залежна змінна щодо незалежної змінної. У обох Figure$\PageIndex{9}$ і Figure залежна змінна є$\PageIndex{10}$,$y$ а незалежна змінна є$x$.

рис. 3.3.9.png — Малюнок$\PageIndex{9}$: Ця лінія йде вниз повільніше, ніж лінія праворуч.

Малюнок 3.3.10.png — Малюнок$\PageIndex{10}$: Ця лінія йде вниз швидше, ніж лінія зліва.

Відніміть координати точки$P(−3,1)$ з координат точки$Q(3,−1)$.

\[\begin{aligned} \text { Slope of first line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-1-1}{3-(-3)} \\ &=\dfrac{-2}{6} \\ &=-\dfrac{1}{3} \end{aligned} \nonumber \]

Відніміть координати точки$R(−2,4)$ з координат точки$S(2,−4)$.

\[\begin{aligned} \text { Slope of second line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4-4}{2-(-2)} \\ &=\dfrac{-8}{4} \\ &=-2 \end{aligned} \nonumber \]

Зверніть увагу, що обидві лінії йдуть вниз і обидві мають негативні нахили. Також врахуйте, що величина (абсолютне значення) ухилу другої лінії більше, ніж величина ухилу першої лінії. Це узгоджується з тим, що друга лінія рухається вниз швидше, ніж перша.

Вправа$\PageIndex{5}$

Обчислити нахил лінії, що проходить через точки$P(−3,3)$ and $Q(3,−5)$. Then compute the slope of the line passing through the points $R(−4,1)$ and $S(4,−3)$, and compare the two slopes. Which line is steeper?

Відповідь: Перша лінія має нахил$−4/3$, а друга - ухил$−1/2$. Перша лінія крутіше.

А як щодо ухилів вертикальних і горизонтальних ліній?

Приклад$\PageIndex{6}$

Обчисліть ухили вертикальних і горизонтальних ліній, що проходять через точку$(2,3)$.

Рішення

Спочатку намалюйте ескіз вертикальних і горизонтальних ліній, що проходять через точку (2,3). Далі виберіть другу точку на кожній лінії, як показано на малюнках$\PageIndex{11}$ і$\PageIndex{12}$.

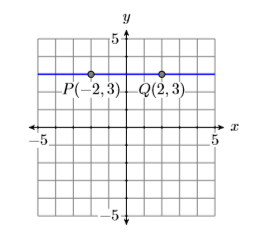
рис. 3.3.11.png — Малюнок$\PageIndex{11}$: Горизонтальна лінія наскрізь$(2,3)$.

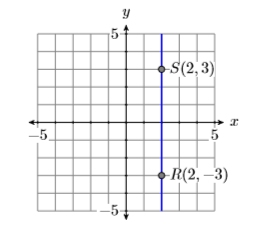
рис. 3.3.12.png — Малюнок$\PageIndex{12}$: Вертикальна лінія наскрізь$(2,3)$.

Ухили горизонтальних і вертикальних ліній розраховуються наступним чином.

Відніміть координати точки$P(−2,3)$ з координат точки$Q(2,3)$.

\[\begin{aligned} \text { Slope of horizontal line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-3}{2-(-2)} \\ &=\dfrac{0}{4} \\ &=0 \end{aligned} \nonumber \]

Таким чином, нахил горизонтальної лінії дорівнює нулю, що має сенс тому, що горизонтальна лінія ні йде в гору, ні вниз.

Відніміть координати точки$(2,−3)$ з координат точки$S(2,3)$.

\[\begin{aligned} \text { Slope of vertical line } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-(-3)}{2-2} \\ &=\dfrac{6}{0} \\ &=\text { undefined } \end{aligned} \nonumber \]

Ділення на нуль не визначено. Отже, нахил вертикальної лінії невизначений. Знову ж таки, це має сенс, оскільки гірські лінії стають крутішими і крутішими, їх схили збільшуються без обмежень.

Вправа$\PageIndex{6}$

Обчисліть ухили вертикальних і горизонтальних ліній, що проходять через h точку$(−4,1)$.

Відповідь: Нахил вертикальної лінії невизначений. Ухил другої лінії -$0$.

Геометрія нахилу прямої

Ми починаємо наше геометричне обговорення нахилу прямої з прикладу, обчислюючи нахил лінії, що проходить через точки$P(2,3)$ і$Q(8,8)$. Перш ніж ми почнемо, ми спочатку обчислимо зміну$y$$x$ та зміну, віднімаючи координати точки$P(2,3)$ з координат точки$Q(8,8)$.

\[\begin{aligned} \mathrm{Slope} &=\dfrac{\Delta y}{\dfrac{\Delta x}{\Delta x}} \\ &=\dfrac{8-3}{8-2} \\ &=\dfrac{5}{6} \end{aligned} \nonumber \]

Таким чином, нахил лінії через точки$P(2,3)$ і$Q(8,8)$ є$5/6$.

Щоб використовувати геометричний підхід до знаходження нахилу лінії, спочатку проведіть лінію через точки$P(2,3)$ і$Q(8,8)$ (див. Малюнок$\PageIndex{13}$). Далі намалюйте прямокутний трикутник зі сторонами, паралельними горизонтальній і вертикальній осях, використовуючи точки$P(2,3)$ і$Q(8,8)$ як вершини. При переході від точки$P$ до$R$ точки на малюнку зверніть увагу$\PageIndex{13}$, що зміна$x$ є$\Delta x=6$ (порахуйте галочки ¹).

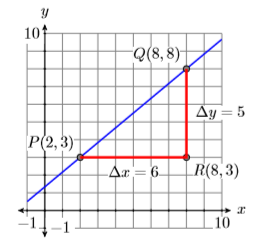
рис. 3.3.13.png — Малюнок$\PageIndex{13}$: Визначення нахилу прямої з графіка.

Коли ви потім рухаєтеся від точки$R$ до точки$Q$, зміна$y$ є$\Delta y=5$ (порахуйте галочки). Таким чином, нахил - це саме те$\Delta y / \Delta x=5 / 6$, що ми отримали в попередньому обчисленні.

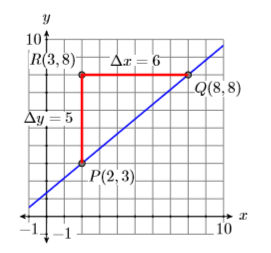
рис. 3.3.14.png — Малюнок$\PageIndex{14}$: Визначення нахилу прямої з графіка.

Для контрасту, на малюнку$\PageIndex{14}$, ми почали в точці$P(2,3)$, потім перемістили вгору$5$ одиниці і праві$6$ одиниці. Однак зміна все ще$y$ є,$\Delta y=5$ і зміна все ще$x$ відбувається, коли$\Delta x=6$ ми рухаємося від точки$P(2,3)$ до точки$Q(8,8)$. Значить, ухил все ще$\Delta y / \Delta x=5 / 6$.

Підйом над бігом

На малюнку е$\PageIndex{14}$ починаємо в точці$P(2,3)$, потім «піднімаємо»$5$ одиниці, потім «запускаємо»$6$ одиниці вправо. З цієї причини деякі люблять думати про схил як «підйом над бігом».

Розглянемо другий приклад, показаний на малюнку$\PageIndex{15}$. Зверніть увагу, що лінія нахиляється вниз, тому ми очікуємо, що нахил буде негативним числом.

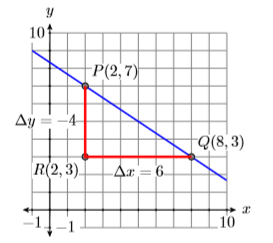
рис. 3.3.15.png — Малюнок$\PageIndex{15}$: Визначення нахилу прямої з графіка.

На малюнку$\PageIndex{15}$ ми намалювали прямокутний трикутник зі сторонами, паралельними горизонтальній і вертикальній осях, використовуючи точки$P(2,7)$ і$Q(8,3)$ як вершини. Коли ви рухаєтеся від точки$P$ до$R$ точки на малюнку$\PageIndex{15}$, зміна$y$ є$\Delta y=-4$ (порахуйте галочки і зверніть увагу, що ваші значення y зменшуються при переході від$P$ до$R$). Коли ви рухаєтеся від точки$R$ до точки$Q$, зміна$x$ є$\Delta x=6$ (порахуйте галочки і зверніть увагу, що ваші значення$x$ збільшуються при переході від$R$ до$Q$). При цьому «підйом» негативний, в той час як «біг» - позитивний.

Таким чином, нахил є$\Delta y / \Delta x=-4 / 6$, або$−2/3$. Зверніть увагу, що нахил негативний, як передбачалося.

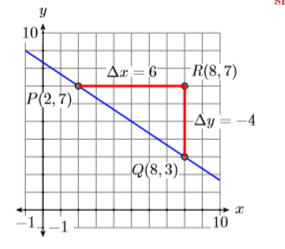
рис. 3.3.16.png — Малюнок$\PageIndex{16}$: Визначення нахилу прямої з графіка.

На малюнку$\PageIndex{16}$ ми намалювали наш трикутник на протилежній стороні лінії. У цьому випадку, коли ви рухаєтеся від точки$P$ до$R$ точки на малюнку$\PageIndex{16}$, зміна$x$ відбувається$\Delta x=6$ (порахуйте галочки і зверніть увагу, що ваші значення$x$ збільшуються при переході від$P$ до$R$). Коли ви рухаєтеся від точки$R$ до точки$Q$, зміна$y$ є$\Delta y=-4$ (порахуйте галочки і зверніть увагу, що ваші значення$y$ зменшуються при переході від$R$ до$Q$). Таким чином, ухил все одно$\Delta y / \Delta x=-4 / 6$, або$−2/3$.

Ми можемо перевірити наші геометричні розрахунки ухилу, віднімаючи координати точки$P(2,7)$ з точки$Q(8,3)$.
\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{3-7}{8-2} \\ &=\dfrac{-4}{6} \\ &=-\dfrac{2}{3} \end{aligned} \nonumber \]

Це узгоджується з розрахунками, зробленими на рисунках$\PageIndex{15}$ і$\PageIndex{16}$.

Давайте розглянемо остаточний приклад.

Приклад$\PageIndex{7}$

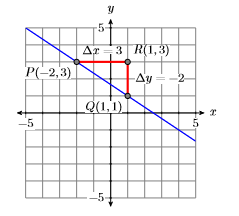
Намалюйте лінію, що проходить через точку$(−2,3)$ з нахилом$−2/3$.

Рішення

Ухил є$−2/3$, тому лінія повинна йти вниз. На малюнку$\PageIndex{17}$ ми починаємо з точки$P(−2,3)$, рухаємо$3$ праві одиниці в точку$R(1,3)$, потім рухаємо вниз$2$ одиниці до точки$Q(1,1)$. Проведіть лінію через точки$P$$Q$ і все готово.

рис. 3.3.17.png — Малюнок$\PageIndex{17}$: Почніть з$P(−2,3)$, потім рухайтеся вправо$3$ і вниз$2$. Отримана лінія має нахил$−2/3$.

На малюнку$\PageIndex{18}$ ми використовуємо інший підхід, який призводить до того ж рядка. Почніть з точки$P(−2,3)$, рухайте вниз$4$ одиниці до точки$R(−2,−1)$, потім$6$ праві одиниці в точку$Q(4,−1)$. Намалюйте лінію через точки$P$$Q$ і все готово.

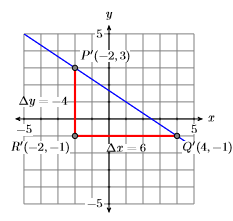
рис. 3.3.18.png — Малюнок$\PageIndex{18}$: Починаючи з$P(−2,3)$ і рухаючись вниз$4$ і вправо$6$ також дає нахил$−2/3$.

Трикутник$PQR$ на малюнку$\PageIndex{17}$ схожий на трикутник$PQR$ на малюнку$\PageIndex{18}$, тому їх сторони пропорційні. Отже, нахил лінії через точки$P(−2,3)$ і$Q(4,−1)$,

\[\begin{aligned} \text { Slope } &=\dfrac{\Delta y}{\Delta x} \\ &=\dfrac{-4}{6} \\ &=-\dfrac{2}{3} \end{aligned} \nonumber \]

зводиться до нахилу лінії через точки$P$ і$Q$ на рис$\PageIndex{17}$.

Вправа$\PageIndex{7}$

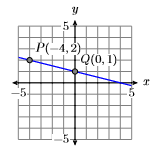
Намалюйте лінію, що проходить через точку$(−4,2)$ with slope $−1/4$.

Відповідь: $Вправа 3.3.7.png$

Короткий зміст фактів про нахил лінії

Ми представляємо короткий виклад фактів, вивчених у цьому розділі.

Нахил лінії - це швидкість, з якою залежна змінна змінюється відносно незалежної змінної. Якщо$y$ є залежною змінною і$x$ є незалежною змінною, то нахил -$\Delta y$ це те,\[\text {Slope}=\dfrac{\Delta y}{\Delta x} \nonumber \] де зміна$y$ (різниця в$y$) і$\Delta x$ є зміною$x$ (різниця в$x$).
Якщо лінія має позитивний нахил, то лінія нахиляється вгору, коли ви «підмітаєте очі зліва направо». Якщо дві лінії мають позитивний ухил, то лінія з більшим ухилом піднімається швидше.
Якщо лінія має негативний нахил, то лінія нахиляється вниз, коли ви «підмітаєте очі зліва направо». Якщо дві лінії мають негативний нахил, то лінія, що має нахил з більшою величиною, падає швидше.
Горизонтальні лінії мають ухил нульовий.
Вертикальні лінії мають невизначений нахил.

Посилання

¹ Під час підрахунку галочок переконайтеся, що ви знаєте суму, яку представляє кожна галочка. Наприклад, якщо кожна галочка представляє дві одиниці, а ви вважаєте шість галочок при оцінці зміни в$x$, то$\Delta x=12$.