9.2: Антидериватив
- Page ID
- 54352
Ви витратили багато уроків, дізнаючись про те, як знайти похідну, f′ (x) функції f (x) та процес диференціації. Це не повинно бути дивно, що буде ім'я для функції f (x), або сімейства функцій, які можуть генерувати f′ (x) при диференціації: f (x) і f′ (x) є парою обернених функцій, а f (x) називається антипохідним від f′ (x). Перш ніж продовжити урок, спробуйте перерахувати функції, які є парами антидеривативів та похідних?
Антидериватив
Почнемо з цього і представимо ідею антидериватива функції.
Функція F (x) називається антипохідною функції f, якщо F′ (x) =f (x) для всіх x у області f.
Як використовується це визначення?
Розглянемо функцію\( f(x)=3x^2 \nonumber\).
Чи можете ви придумати функцію F (x) таку, що F′ (x) = f (x)? Ви повинні бути в змозі думати про багато з них.
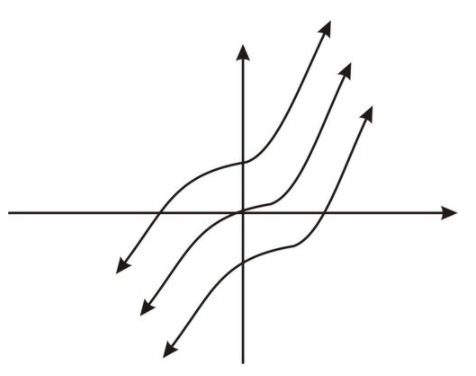
Оскільки ми диференціюємо F (x), щоб отримати f (x), ми бачимо, що\( F(x)=x^3+C \nonumber\) буде працювати для будь-якої константи C Графічно, ми можемо думати про множину всіх антипохідних як вертикальні перетворення графа\( F(x)=x^3 \nonumber\). На малюнку показані два таких перетворення.
CC ЗА NC-SA
З нашим визначенням та початковим прикладом ми тепер шукаємо формалізацію визначення та розробляємо деякі корисні правила для обчислювальних цілей, і починаємо бачити деякі програми.
Введення в невизначені інтеграли
Процес знаходження антипохідних називається антидиференціацією, частіше його називають інтеграцією. Ось як вказується інтеграція та як вона працює:
F′ (х) = ф (х)... Почніть з диференціального рівняння, яке представляє визначення антипохідної
\( \int F′(x)dx=\int f(x)dx \nonumber\)... Викликати операцію інтеграції (антидиференціації) за допомогою спеціального символу.
\( F(x)+C= \int f(x)dx \nonumber\)... Отримати антидериватив F (x) і константу інтеграції, C.
\( \int f(x)dx=F(x)+C \nonumber\)... Зауважте, що якщо ми розмежовуємо обидві сторони, ми повернемо вихідне рівняння:
\[ \frac{d}{dx}[ \int f(x)dx]=f(x)=\frac{d}{dx}[F(x)+C]=F′(x) \nonumber\]
Ми називаємо f (x) dx як «невизначений інтеграл f (x) по відношенню до x». Функція f (x) називається цілою, а константа C називається константою інтеграції . Нарешті символ dx вказує на те, що ми повинні інтегруватися щодо x.
Використовуючи це позначення, ми б узагальнили останній приклад наступним чином:
\[ \int 3x^2dx=x^3+C \nonumber\]
Тепер розглянемо функцію f (x) = cosx
Чи можете ви придумати функцію F (x) таку, що F′ (x) = f (x)?
Якби ви сказали F (x) =sinx+c ви були б правильними, і ось як це буде написано.
f (x) = F′ (х). Почніть з диференціального рівняння, яке представляє визначення антипохідної
COSX = F′ (х). Замінник f (x)
\( \int cosx dx= \int F′(x)dx \nonumber\). Викликати операцію інтеграції (антидиференціації) за допомогою спеціального символу.
\( \int cosx dx=F(x)+C \nonumber\). Отримати антидериватив F (x) і константу інтеграції, C.
\( \int cosx dx=sinx+C \nonumber\). Ми знаємо F (x) = sinx, тому що якщо ми диференціюємо обидві сторони, ми повернемо вихідне рівняння.
Ми розглянули похідні ряду функцій через поняття числення і можемо скласти список функцій та їх антипохідних, як показано нижче.
|
Функція f (x) |
Антидериватив\( /int f(x)dx=F(x)+C \nonumber\) |
| 1 | Х+С |
| х |
\( \frac{x^2}{2}+C \nonumber\) |
|
\( x^2 \nonumber\) |
\( \frac{x^3}{3}+C \nonumber\) |
|
\( x^n,\nonumber\) n−1 |
\( \frac{x^{n+1}}{n+1}+C \nonumber\) |
|
\( \frac{1}{x} \nonumber\) |
\( lnx+C \nonumber\) |
|
гріх |
−COSx+C |
|
кокс |
Sinx+C |
|
\( sec^2x \nonumber\) |
Танк+С |
|
\( csc^2x \nonumber\) |
−COTX+C |
|
сектанс |
Секх+С |
|
cscxcotx |
−CSCX+C |
|
\( e^x \nonumber\) |
\( e^x+C \nonumber\) |
|
\( b^x \nonumber\) b> 0 |
\( \frac{b^x}{lnb}+C \nonumber\) |
|
\( \frac{1}{xlnb} \nonumber\) |
\( log_bx+C \nonumber\) |
Як і у випадку з диференціацією, існує кілька правил для роботи з сумою та різницею інтегровних функцій.
Основні правила інтеграції
Якщо f і g - інтегровні функції, а C - константа, то:
\[ \int [f(x)+g(x)]dx= \int f(x)dx+ \int g(x)dx \nonumber\],
\[ \int [f(x)−g(x)]dx= \int f(x)dx− \int g(x)dx \nonumber\],
\[ \int [Cf(x)]dx=C \int f(x)dx \nonumber\]
Обчислити наступний невизначений інтеграл.
\[ \int [2x^3+3x^2−1x]dx \nonumber\]
Використовуючи наші правила, ми маємо
\[ \int [2x^3+3x^2−1x]dx=2 \int x^3dx+3 \int \frac{1}{x^2}dx− \int \frac{1}{x}dx \nonumber\]
\[ =2(\frac{x^4}{4})+3(\frac{x^{−1}}{−1})−lnx+C \nonumber\]
\[ =\frac{x^4}{2}−\frac{3}{x}−lnx+C \nonumber\].
Зверніть увагу, що іноді наші правила потрібно трохи змінити через операції з константами.
Приклади
Приклад 1
Раніше вас попросили спробувати перерахувати функції, які є парами антидеривативів та похідних. Таким чином ви представляєте результати диференціації та інтеграційних операцій. Якщо все, що ви зробили, це перерахувати функцію, яку диференціюють як антидериватив, це правильно. На даний момент ви зрозуміли, що існує сімейство антипохідних, з яких ви могли б вибрати, кожен з яких відрізняється постійною інтеграцією.
Приклад 2
Обчислити такий невизначений інтеграл:
\[ \int e^{3x}dx \nonumber\].
Спочатку зауважимо, що наше правило інтеграції експоненціальних функцій тут не працює, оскільки ddxe3x=3e3x. Однак, якщо ми пам'ятаємо розділити вихідну функцію на постійну, то ми отримаємо правильну антидериватив і маємо
\[ \int e^{3x}dx=\frac{e^{3x}}{3}+C \nonumber\].
Тепер ми можемо повторно викласти правило в більш загальному вигляді як
\[ \int e^{kx}dx= \frac{e^{kx}}{3}+C \nonumber\].
Рецензія
Для #1 -6 знайдіть антипохідну функції
- \( f(x)=1−3x^2−6x \nonumber\)
- \( f(x)=x−x^\{frac{2}{3}} \nonumber\)
- \( f(x)=(2x+1)^{\frac{1}{5}} \nonumber\)
- \( f(x)=cosx−x \nonumber\)
- \( f(x)=x^5−7x^2+2 \nonumber\)
- \(f(x)=e^{−2x}+e^x \nonumber\)
Для #7 -12 знайти невизначений інтеграл
- \ (\ int (2+\ sqrt {5}) х\ номер\]
- \( \int 2(x−3)^3dx \nonumber\)
- \( \int (x^2⋅x^\frac{1}{3})dx \nonumber\)
- \( \int (x+\frac{1}{x^4\sqrt{x}})dx \nonumber\)
- \( (cosx+2sinx)dx \nonumber\)
- \( \int 2sinxcosxdx \nonumber\)
- Вирішити диференціальне рівняння\( f′(x)=4x^3−3x^2+x−3 \nonumber\).
- Знайти антипохідну F (x) функції\( f(x)=2e^{2x}+x−2 \nonumber\), яка задовольняє F (0) =5.
- Оцінити невизначений інтеграл\( \int |x|dx \nonumber\) (Підказка: Вивчіть графік f (x) =|x|.)
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.1.
Лексика
| Термін | Визначення |
|---|---|
| антидериватив | Антидериватив - це функція, яка змінює похідну. Функція A є антипохідною функції B, якщо функція B є похідною функції А. |
| антидиференціювання | Процес знаходження антипохідних називається антидиференціацією, частіше його називають інтеграцією. |
| константа інтеграції | Константа інтеграції - це константа C у рівнянні f (x) dx=F (x) +C, що стосується функції f (x) та антипохідної F. |
| цілісний | Цілим числом є аргумент f (x) у невизначеному інтегралі f (x) dx. |
| інтеграція | Процес знаходження антипохідних іноді називають антидиференціацією, але частіше називають інтеграцією. |
Додаткові ресурси
PLIX: Грайте, вчіться, взаємодійте, досліджуйте - антидериватив: збираючи його разом
Практика: Антидериватив
Реальний світ: Скелясті гори Високі