5.2: Певний інтеграл
- Page ID
- 61822
- Створіть визначення певного інтеграла.
- Поясніть терміни integrand, межі інтеграції та змінну інтеграції.
- Поясніть, коли функція інтегрується.
- Опишіть зв'язок між певним інтегралом і чистою площею.
- Використовуйте геометрію та властивості певних інтегралів для їх оцінки.
- Обчисліть середнє значення функції.
У попередньому розділі ми визначили площу під кривою через суми Рімана:
\[A=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
Однак це визначення прийшло з обмеженнями. Ми\(f(x)\) вимагали бути безперервними і ненегативними. На жаль, реальні проблеми не завжди відповідають цим обмеженням. У цьому розділі ми розглянемо, як застосувати поняття площі під кривою до більш широкого набору функцій за допомогою використання певного інтеграла.
Визначення та позначення
Певний інтеграл узагальнює поняття площі під кривою. Ми піднімаємо вимоги, які є\(f(x)\) неперервними і невід'ємними, і визначаємо певний інтеграл наступним чином.
Якщо\(f(x)\) є функцією, визначеною на\([a,b],\) інтервалі, то певний інтеграл\(f\)\(a\)\(b\) from to задається
\[∫^b_af(x)\,dx=\lim_{n→∞} \sum_{i=1}^nf(x^∗_i)Δx, \nonumber \]
за умови, що ліміт існує. Якщо ця межа існує, функція\(f(x)\), як кажуть\([a,b]\), інтегрується або є інтегровною функцією.
Інтегральний символ в попередньому визначенні повинен виглядати звично. Подібні позначення ми бачили в розділі «Застосування похідних», де ми використовували невизначений інтегральний символ (без\(a\) і\(b\) вище і нижче) для представлення антидериватива. Хоча позначення для невизначеного інтеграла можуть виглядати схожими на позначення для певного інтеграла, вони не однакові. Певний інтеграл - це число. Невизначений інтеграл - це сімейство функцій. Пізніше в цьому розділі ми розглянемо, як ці поняття пов'язані між собою. Однак пильна увага завжди повинна приділятися позначенню, щоб ми знали, чи працюємо ми з певним інтегралом або невизначений інтеграл.
Інтегральна позначення сягає кінця сімнадцятого століття і є одним із внесків Готфріда Вільгельма Лейбніца, який часто вважається співвідкривачем обчислення разом з Ісааком Ньютоном. Символ інтеграції\(∫\) - подовжений\(S\), що передбачає сигму або підсумовування. На певному інтегралі, вище і нижче символу підсумовування є межі інтервалу,\([a,b].\) числа\(a\) і\(b\)\(x\) -значення і називаються межами інтеграції; конкретно,\(a\) є нижньою межею і\(b\) є верхньою межею. Для уточнення ми використовуємо слово limit двома різними способами в контексті певного інтеграла. По-перше, ми говоримо про межу суми, як\(n→∞.\) По-друге, межі регіону називаються межею інтеграції.
Ми називаємо функцію\(f(x)\) integrand, а\(dx\) вказує на те, що\(f(x)\) є функцією щодо\(x\), називається змінною інтеграції. Зверніть увагу, що, як і індекс у сумі, змінна інтеграції є фіктивною змінною і не впливає на обчислення інтеграла. Ми могли б використовувати будь-яку змінну, яка нам подобається, як змінна інтеграції:
\[∫^b_af(x)\,dx=∫^b_af(t)\,dt=∫^b_af(u)\,du \nonumber \]
Раніше ми обговорювали той факт, що якщо\(f(x)\) є безперервним,\([a,b],\) то межа\(\displaystyle \lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\) існує і є унікальною. Це призводить до наступної теореми, яку ми констатуємо без доказів.
Якщо\(f(x)\) безперервно\([a,b]\) увімкнено, то\(f\) інтегрується на\([a,b].\)
Функції, які не є безперервними, все ще\([a,b]\) можуть бути інтегрованими, залежно від характеру розривів. Наприклад, функції з скінченним числом стрибкових розривів або знімних розривів на замкнутому інтервалі інтегруються.
Тут також варто відзначити, що ми зберегли використання звичайного розділу в сумах Рімана. Це обмеження не є строго необхідним. Будь-який розділ може бути використаний для формування суми Рімана. Однак, якщо для визначення певного інтеграла використовується нерегулярний розділ, недостатньо взяти межу, оскільки кількість підінтервалів переходить до нескінченності. Замість цього ми повинні взяти межу, оскільки ширина найбільшого субінтервалу йде до нуля. Це вводить трохи складніші позначення в наших межах і ускладнює обчислення, не отримуючи багато додаткового розуміння, тому ми дотримуємося регулярних розділів для сум Рімана.
Використовуйте визначення визначеного інтеграла для оцінки\(\displaystyle ∫^2_0x^2\,dx.\) Використовуйте наближення правої точки для генерації суми Рімана.
Рішення
Спочатку ми хочемо встановити суму Рімана. Виходячи з меж інтеграції, ми маємо\(a=0\) і\(b=2\). Для\(i=0,1,2,…,n\), нехай\(P={x_i}\) буде регулярний розділ\([0,2].\) Тоді
\[Δx=\dfrac{b−a}{n}=\dfrac{2}{n}. \nonumber \]
Оскільки ми використовуємо наближення правої кінцевої точки для генерації сум Рімана, для кожного\(i\) нам потрібно обчислити значення функції в правій кінцевій точці інтервалу\([x_{i−1},x_i].\) Права кінцева точка інтервалу\(x_i\), а оскільки\(P\) є регулярним розділом,
\[x_i=x_0+iΔx=0+i\left[\dfrac{2}{n}\right]=\dfrac{2i}{n}.\nonumber \]
Таким чином, значення функції в правій кінцевій точці інтервалу дорівнює
\[f(x_i)=x^2_i=\left(\dfrac{2i}{n}\right)^2=\dfrac{4i^2}{n^2}.\nonumber \]
Тоді сума Рімана набуває вигляду
\[\sum_{i=1}^nf(x_i)Δx=\sum_{i=1}^n\left(\dfrac{4i^2}{n^2}\right)\dfrac{2}{n}=\sum_{i=1}^n\dfrac{8i^2}{n^3}=\dfrac{8}{n^3}\sum_{i=1}^ni^2.\nonumber \]
Використовуючи формулу підсумовування для\(\displaystyle \sum_{i=1}^ni^2\), ми маємо
\[\begin{align*} \sum_{i=1}^nf(x_i)Δx &=\dfrac{8}{n^3}\sum_{i=1}^ni^2 \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{n(n+1)(2n+1)}{6}\right] \\[4pt] &=\dfrac{8}{n^3}\left[\dfrac{2n^3+3n^2+n}{6}\right] \\[4pt] &=\dfrac{16n^3+24n^2+n}{6n^3} \\[4pt] &=\dfrac{8}{3}+\dfrac{4}{n}+\dfrac{1}{6n^2}. \end{align*}\]
Тепер, щоб обчислити певний інтеграл, нам потрібно взяти межу як\(n→∞\). Отримуємо
\ [\ почати {вирівнювати*} ^2_0x^2dx &=\ lim_ {n→∞}\ сума_ {i=1} ^nf (x_i) Δx\\ [4pt]
&=\ lim_ {n→∞}\ ліворуч (\ dfrac {8} {3} +\ dfrac {4} {n} +\ dfrac {1} n^2}\ праворуч)\\ [4pt]
&=\ lim_ {n→∞}\ ліворуч (\ dfrac {8} {3}\ праворуч) +\ lim_ {n→∞}\ ліворуч (\ dfrac {4} {n}\ праворуч) +\ lim_ {n→∞}\ ліворуч (\ dfrac {1} {6n^2}\ праворуч) [4 пт]
&=\ dfrac {8} {3} +0+0=\ dfrac {8} {3}. \ end {вирівнювати*}\]
Використовуйте визначення певного інтеграла для оцінки\(\displaystyle ∫^3_0(2x−1)\,dx\).
Використовуйте наближення правої кінцевої точки для генерації суми Рімана.
- Підказка
-
Використовуйте стратегію розв'язання з Example\(\PageIndex{1}\).
- Відповідь
-
6
Оцінка визначених інтегралів
Оцінка певних інтегралів таким чином може бути досить стомлюючою через складність обчислень. Пізніше в цьому розділі ми розробляємо методи оцінки визначених інтегралів без обмеження сум Рімана. Однак наразі ми можемо покладатися на те, що певні інтеграли представляють площу під кривою, і ми можемо оцінити певні інтеграли, використовуючи геометричні формули для обчислення цієї площі. Ми робимо це, щоб підтвердити, що певні інтеграли дійсно представляють області, так що ми можемо потім обговорити, що робити у випадку кривої функції, що падає нижче\(x\) -осі.
Скористайтеся формулою площі кола для оцінки\(\displaystyle ∫^6_3\sqrt{9−(x−3)^2}\,dx\).
Рішення
Функція описує півколо з радіусом 3. Щоб знайти
\[∫^6_3\sqrt{9−(x−3)^2}\,dx \nonumber \]
ми хочемо знайти площу під кривою через\([3,6].\) інтервал Формула для площі кола є\(A=πr^2\). Площа півкола - це всього лише половина площі кола, або\(A=\dfrac{1}{2}πr^2\). Затінена область на малюнку\(\PageIndex{1}\) охоплює половину півкола, або\(A=\dfrac{1}{4}πr^2\). Таким чином,
\[∫^6_3\sqrt{9−(x−3)^2}\,dx=\dfrac{1}{4}π(3)^2=\dfrac{9}{4}π≈7.069. \nonumber \]
![Графік півкола в квадраті один за інтервалом [0,6] з центром в (3,0). Область під кривою над інтервалом [3,6] заштрихована синім кольором.](https://math.libretexts.org/@api/deki/files/12421/5.2.1.png)
Скористайтеся формулою площі трапеції для оцінки\(\displaystyle ∫^4_2(2x+3)\,dx\).
- Підказка
-
Графік функції\(f(x)\) і обчислення площі під функцією на інтервалі\([2,4].\)
- Відповідь
-
18 квадратних одиниць
Площа і певний інтеграл
Коли ми визначили певний інтеграл, ми зняли вимогу, яка є\(f(x)\) невід'ємною. Але як ми інтерпретуємо «область під кривою»,\(f(x)\) коли негативна?
Чистий підписаний Площа
Повернемося до суми Рімана. Розглянемо, наприклад, функцію\(f(x)=2−2x^2\) (показану на малюнку\(\PageIndex{2}\)) на інтервалі\([0,2]\). Використовуйте\(n=8\) та виберіть {\(x^∗_i\)} як ліву кінцеву точку кожного інтервалу. Побудувати прямокутник на кожному підінтервалі висоти\(f(x^∗_i)\) і ширини\(Δx\). Коли\(f(x^∗_i)\) позитивний, твір\(f(x^∗_i)Δx\) представляє площу прямокутника, як і раніше. Однак, коли\(f(x^∗_i)\) негативний, твір\(f(x^∗_i)Δx\) являє собою негатив площі прямокутника. Сума Рімана тоді стає
\[\sum_{i=1}^8f(x^∗_i)Δx= (\text{Area of rectangles above the }x\text{-axis})−(\text{Area of rectangles below the }x\text{-axis}) \nonumber \]
![Графік низхідної параболи над [-1, 2] з вершиною в (0,2) і x-перехоплює в (-1,0) і (1,0). Вісім прямокутників намальовані рівномірно над [0,2] з висотами, визначеними значенням функції в лівих кінцевих точках кожного.](https://math.libretexts.org/@api/deki/files/2586/CNX_Calc_Figure_05_02_003.jpeg)
Беручи\(n→∞,\) межу, оскільки сума Рімана наближається до площі між кривою над\(x\) -віссю та\(x\) -віссю, менша площа між кривою нижче\(x\) -осі та\(x\) віссю, як показано на малюнку\(\PageIndex{3}\). Потім,
\[\int^2_0f(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(c_i)Δx=A_1−A_2. \nonumber \]
Величина\(A_1−A_2\) називається сітчастою областю підпису.
![Графік низхідної параболи над [-2, 2] з вершиною в (0,2) і x-перехоплює в (-1,0) і (1,0). Площа в квадранті один під кривою затінена синім кольором і позначена A1. Площа в четвертому квадранті над кривою і ліворуч від x = 2 затінена синім кольором і позначена A2.](https://math.libretexts.org/@api/deki/files/2587/CNX_Calc_Figure_05_02_002.jpeg)
Зверніть увагу, що сітка підписана область може бути позитивною, негативною або нульовою. Якщо площа над\(x\) віссю -більше, чиста підписана область є додатною. Якщо площа під\(x\) віссю -більше, чиста підписана область від'ємна. Якщо області вище і нижче\(x\) -осі рівні, то чиста підписана площа дорівнює нулю.
Знайти площу з чистим знаком між кривою функції\(f(x)=2x\) та\(x\) -віссю за інтервал\([−3,3].\)
Рішення
Функція створює пряму лінію, яка утворює два трикутника: один від\(x=−3\) до,\(x=0\) а інший від\(x=0\) до\(x=3\) (рис.\(\PageIndex{4}\)). Використовуючи геометричну формулу для площі трикутника\(A=\dfrac{1}{2}bh\), площа трикутника\(A_1\), над віссю, дорівнює
\(A_1=\dfrac{1}{2}3(6)=9\),
де\(3\) знаходиться підстава і\(2(3)=6\) - висота. Площа трикутника\(A_2\), нижче осі, дорівнює
\(A_2=\dfrac{1}{2}(3)(6)=9,\)
де\(3\) знаходиться підстава і\(6\) - висота. Таким чином, чиста площа дорівнює
\(\displaystyle ∫^3_{−3}2x\,dx=A_1−A_2=9−9=0.\)
![Графік зростаючої лінії над [-6, 6], що проходить через початок і (-3, -6) і (3,6). Область під лінією в квадранті один над [0,3] затінена синім кольором і позначена A1, а область над лінією в квадранті три над [-3,0] затінена синім кольором і позначена A2.](https://math.libretexts.org/@api/deki/files/12422/5.2.2.png)
Аналіз
Якщо\(A_1\) площа над\(x\) -віссю і\(A_2\) є площею нижче\(x\) -осі, то чиста площа дорівнює\(A_1−A_2\). Оскільки площі двох трикутників рівні, чиста площа дорівнює нулю.
Знайдіть сітку підписану область\(f(x)=x−2\) над інтервалом\([0,6]\), проілюстрованим на наступному зображенні.
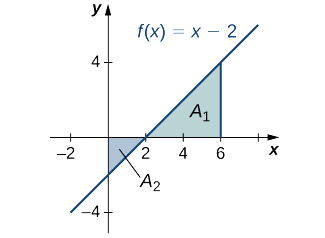
- Підказка
-
Скористайтеся методом розв'язання, описаним у прикладі\(\PageIndex{3}\).
- Відповідь
-
6
Загальна площа
Одним із застосувань визначеного інтеграла є знаходження зсуву, коли задана функція швидкості. Якщо\(v(t)\) представляє швидкість об'єкта як функцію часу, то область під кривою говорить нам, наскільки далеко об'єкт знаходиться від початкового положення. Це дуже важливе застосування певного інтеграла, і ми розглянемо його більш детально далі в розділі. Наразі ми просто розглянемо деякі основи, щоб відчути, як це працює, вивчаючи постійні швидкості.
Коли швидкість є постійною, площа під кривою - це просто швидкість часу часу. Ця ідея вже дуже знайома. Якщо автомобіль від'їжджає від початкового положення по прямій зі швидкістю\(70\) миль/год протягом декількох\(2\) годин, то він знаходиться в\(140\) милі від початкового положення (рис.\(\PageIndex{5}\)). Використовуючи інтегральні позначення, ми маємо
\[∫^2_0 70\,dt=140 \,\text{miles}. \nonumber \]
![Графік у квадранті 1 з віссю x, позначеною як t (години) та віссю y, позначеною як v (mi/hr). Площа під лінією v (t) = 75 заштрихована синім кольором над [0,2].](https://math.libretexts.org/@api/deki/files/2590/CNX_Calc_Figure_05_02_015.jpeg)
У контексті переміщення, чиста підписана площа дозволяє нам враховувати напрямок. Якщо автомобіль їде прямо на північ зі швидкістю 60 км/год протягом 2 годин, це 120 миль на північ від початкового положення. Якщо автомобіль потім розвернеться і їде на південь зі швидкістю 40 км/год протягом 3 годин, він повернеться в початкове положення (рис.\(\PageIndex{6}\)). Знову ж таки, використовуючи інтегральні позначення, у нас є
\[\int^2_060\,dt+∫^5_2−40\,dt=120−120=0.\nonumber \]
При цьому зміщення дорівнює нулю.
![Графік у квадрантах один та чотири з віссю x, позначеною як t (години) та віссю y, позначеною як v (mi/hr). Перша частина графіка - це лінія v (t) = 60 над [0,2], а площа під лінією в квадранті заштрихована. Друга частина графіка - це лінія v (t) = -40 над [2,5], а область над лінією в четвертому квадранті заштрихована.](https://math.libretexts.org/@api/deki/files/2591/CNX_Calc_Figure_05_02_016.jpeg)
Припустимо, ми хочемо знати, як далеко автомобіль їде в цілому, незалежно від напрямку. У цьому випадку ми хочемо знати площу між кривою та\(t\) -віссю, незалежно від того, чи знаходиться ця область вище або нижче осі. Це називається загальною площею.
Графічно найпростіше думати про обчислення загальної площі, додаючи області над віссю та області нижче осі (замість того, щоб віднімати області нижче осі, як ми це робили з сіткою підписаної області). Для досягнення цього математично ми використовуємо функцію абсолютного значення. Таким чином, загальна відстань, пройдена автомобілем, становить
\[\int^2_0|60|\,dt+∫^5_2|−40|\,dt=∫^2_060\,dt+∫^5_240\,dt=120+120=240.\nonumber \]
Зводячи ці ідеї разом формально, ми викладемо наступні визначення.
\(f(x)\)Дозволяти інтегрується функція, визначена на інтервалі\([a,b]\). \(A_1\)Дозволяти представляти область між\(f(x)\) і\(x\) -вісь, яка лежить над віссю і нехай\(A_2\) представляють область між\(f(x)\) і\(x\) -вісь, яка лежить нижче осі. Потім чиста підписана область між\(f(x)\) і\(x\) -віссю задається
\[∫^b_af(x)\,dx=A_1−A_2. \nonumber \]
Загальна площа між віссю\(f(x)\) і\(x\) -віссю задається
\[∫^b_a|f(x)|\,dx=A_1+A_2. \nonumber \]
Знайти загальну площу між\(f(x)=x−2\) і\(x\) -віссю за інтервал\([0,6].\)
Рішення
Обчисліть\(x\) -перехоплення як\((2,0)\) (встановити\(y=0,\) вирішити для\(x\)). Щоб знайти загальну площу, візьміть область нижче\(x\) -осі над підінтервалом\([0,2]\) і додайте її до площі над\(x\) -віссю на підінтервалі\([2,6]\) (рис.\(\PageIndex{7}\)).
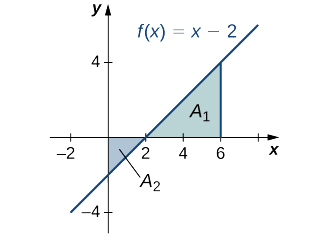
У нас є
\[∫^6_0|(x−2)|\,dx=A_2+A_1. \nonumber \]
Потім, використовуючи формулу для площі трикутника, отримаємо
\[A_2=\dfrac{1}{2}bh=\dfrac{1}{2}⋅2⋅2=2 \nonumber \]
\[A_1=\dfrac{1}{2}bh=\dfrac{1}{2}⋅4⋅4=8. \nonumber \]
Загальна площа, значить, становить
\[A_1+A_2=8+2=10\,\text{units}^2. \nonumber \]
Знайти загальну площу між функцією\(f(x)=2x\) і\(x\) -віссю за інтервал\([−3,3].\)
- Підказка
-
Перегляньте стратегію вирішення у прикладі\(\PageIndex{4}\).
- Відповідь
-
\(18\,\text{units}^2\)
Властивості визначеного інтеграла
Властивості невизначеного інтегралу застосовуються і до визначених інтегралів. Певні інтеграли також мають властивості, які відносяться до меж інтеграції. Ці властивості, поряд з правилами інтеграції, які ми розглянемо далі в цьому розділі, допомагають нам маніпулювати виразами для оцінки певних інтегралів.
1. \[ \begin{equation} ∫^a_af(x)\,dx=0 \end{equation} \nonumber \]
Якщо межі інтеграції однакові, інтеграл є лише рядком і не містить області.
2. \[∫^a_bf(x)\,dx=−∫^b_af(x)\,dx \nonumber \]
Якщо межі змінюються, то поставте негативний знак навпроти інтеграла.
3. \[∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx \nonumber \]
Інтеграл суми - це сума інтегралів.
4. \[∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx \nonumber \]
Інтегралом різниці є різниця інтегралів.
5. \[∫^b_acf(x)\,dx=c∫^b_af(x)\,dx \nonumber \]
для постійних\(c\). Інтеграл добутку константи і функції дорівнює постійній, помноженої на інтеграл функції.
6. \[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx \nonumber \]
Хоча ця формула зазвичай застосовується, коли\(c\) знаходиться між\(a\) і\(b\), формула тримає для всіх значень\(a\), і\(b\), за умови\(c\),\(f(x)\) інтегрується на найбільшому інтервалі.
Використовуйте властивості певного інтеграла для вираження певного інтеграла\(f(x)=−3x^3+2x+2\) через інтервал\([−2,1]\) як суму трьох визначених інтегралів.
Рішення
Використовуючи інтегральні позначення,\(\displaystyle ∫^1_{−2}(−3x^3+2x+2)\,dx.\) ми застосовуємо властивості 3. і 5. щоб отримати
\ [\ begin {вирівнювати*} ^1_ {−2} (−3x^3+2x+2)\, dx =^1_ {−2} −3x^3\, dx+^1_ {−2} 2x\, dx+^1_ {−2} 2\, dx\\ [4pt]
=−3^1_ {−2}, dx+2^1_ {−2} х\, дх+^1_ {−2} 2\, дх. \ end {вирівнювати*}\ nonumber\]
Використовуйте властивості певного інтеграла для вираження певного інтеграла\(f(x)=6x^3−4x^2+2x−3\) через інтервал\([1,3]\) як суму чотирьох визначених інтегралів.
- Підказка
-
Використовуйте стратегію розв'язання з\(\PageIndex{5}\) Example та властивості визначених інтегралів.
- Відповідь
-
\(\displaystyle 6∫^3_1x^3\,dx−4∫^3_1x^2\,dx+2∫^3_1x\,dx−∫^3_13\,dx \)
Якщо відомо, що\(\displaystyle ∫^8_0f(x)\,dx=10\) і\(\displaystyle ∫^5_0f(x)\,dx=5\), знайдіть значення\(\displaystyle ∫^8_5f(x)\,dx\).
Рішення
За майном 6,
\[∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx. \nonumber \]
Таким чином,
\[ \begin{align*} ∫^8_0f(x)\,dx&=∫^5_0f(x)\,dx+∫^8_5f(x)\,dx \\[4pt] 10 &=5+∫^8_5f(x)\,dx \\[4pt] 5 &=∫^8_5f(x)\,dx. \end{align*}\]
Якщо відомо, що\(\displaystyle ∫^5_1f(x)\,dx=−3\) і\(\displaystyle ∫^5_2f(x)\,dx=4\), знайдіть значення\(\displaystyle ∫^2_1f(x)\,dx.\)
- Підказка
-
Використовуйте стратегію розв'язання з Прикладу\(\PageIndex{6}\) та правило про властивості визначених інтегралів.
- Відповідь
-
\(−7\)
Порівняльні властивості інтегралів
Зображення іноді може розповісти нам більше про функцію, ніж результати обчислень. Порівняння функцій за їх графіками, а також за їх алгебраїчними виразами часто може дати нове уявлення про процес інтеграції. Інтуїтивно ми можемо сказати, що якщо функція\(f(x)\) вище іншої функції\(g(x)\), то площа між\(f(x)\) і\(x\) -вісь більше, ніж площа між\(g(x)\) і\(x\) -вісь. Це вірно в залежності від інтервалу, за який проводиться порівняння. Властивості певних інтегралів дійсні чи\(a<b,\,a=b\), або\(a>b\). Наступні властивості, однак, стосуються тільки випадку\(a≤b\), і використовуються, коли ми хочемо порівняти розміри інтегралів.
i. якщо\(f(x)≥0\) для\(a≤x≤b\), то
\[∫^b_af(x)\,dx≥0. \nonumber \]
II. Якщо\(f(x)≥g(x)\) для\(a≤x≤b\), то
\[∫^b_af(x)\,dx≥∫^b_ag(x)\,dx. \nonumber \]
III. Якщо\(m\) і\(M\) є константами такі, що\(m≤f(x)≤M\) для\(a≤x≤b\), то
\[m(b−a)≤∫^b_af(x)\,dx≤M(b−a). \nonumber \]
Порівняйте\(f(x)=\sqrt{1+x^2}\) і\(g(x)=\sqrt{1+x}\) за інтервал\([0,1]\).
Рішення
Графік цих функцій необхідно, щоб зрозуміти, як вони порівнюються протягом інтервалу\([0,1].\) Спочатку, коли графіки на графічному калькуляторі,\(f(x)\) здається, вище\(g(x)\) скрізь. Однак на\([0,1]\) проміжку графіки здаються один на одного. Нам потрібно збільшити масштаб, щоб побачити, що на інтервалі\([0,1],\,g(x)\) знаходиться вище\(f(x)\). Дві функції перетинаються в\(x=0\) і\(x=1\) (рис.\(\PageIndex{8}\)).
![Графік функції f (x) = sqrt (1 + x^2) червоним кольором та g (x) = sqrt (1 + x) синім кольором над [-2, 3]. Функція f (x) з'являється над g (x) за винятком інтервалу [0,1]. Другий, збільшений графік показує цей інтервал більш чітко.](https://math.libretexts.org/@api/deki/files/12425/5.2.5.png)
Ми бачимо з графіка, що за інтервалом\([0,1],\,g(x)≥f(x)\). Порівнюючи інтеграли за вказаний інтервал\([0,1],\) ми також бачимо, що\(\displaystyle ∫^1_0g(x)\,dx≥∫^1_0f(x)\,dx\) (рис.\(\PageIndex{9}\)). Тонка, червоно-затінена область показує, наскільки велика різниця між цими двома інтегралами протягом інтервалу\([0,1].\)
![Графік, що показує функції f (x) = sqrt (1 + x ^ 2) та g (x) = sqrt (1+ x) над [-3, 3]. Площа під g (x) в квадранті один над [0,1] затінюється. Область під g (x) і f (x) включена в цю затінену область. Другий, збільшений графік показує більш чітко, що рівність між функціями тримається лише в кінцевих точках.](https://math.libretexts.org/@api/deki/files/12426/5.2.6.png)
Середнє значення функції
Нам часто потрібно знайти середнє значення набору чисел, наприклад, середній бал тесту. Припустимо, ви отримали наступні оцінки тестів у своєму класі алгебри: 89, 90, 56, 78, 100 та 69. Ваш семестр оцінка є вашим середнім показником тестових балів, і ви хочете знати, яку оцінку очікувати. Ми можемо знайти середнє, додавши всі бали і розділивши на кількість балів. В даному випадку існує шість тестових балів. Таким чином,
\[\dfrac{89+90+56+78+100+69}{6}=\dfrac{482}{6}≈80.33. \nonumber \]
Отже, середній бал тесту становить приблизно 80,33, що перекладається на B − у більшості шкіл.
Однак припустимо, що у нас є функція\(v(t)\), яка дає нам швидкість об'єкта в будь-який час\(t\), і ми хочемо знайти середню швидкість об'єкта. Функція\(v(t)\) приймає на себе нескінченну кількість значень, тому ми не можемо використовувати тільки що описаний процес. На щастя, ми можемо використовувати певний інтеграл, щоб знайти середнє значення такої функції, як ця.
\(f(x)\)Дозволяти бути безперервним протягом інтервалу\([a,b]\) і нехай\([a,b]\) бути розділені на n підінтервалів ширини\(Δx=(b−a)/n\). Виберіть представника\(x^∗_i\) в кожному підінтервалі і\(f(x^∗_i)\) обчислюйте для\(i=1,2,…,n.\) Іншими словами, розгляньте кожен\(f(x^∗_i)\) як вибірку функції над кожним підінтервалом. Потім середнє значення функції може бути наближено як
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}, \nonumber \]
який в основному є тим самим виразом, що використовується для обчислення середнього дискретних значень.
Але ми\(Δx=\dfrac{b−a}{n},\) так знаємо\(n=\dfrac{b−a}{Δx}\), і ми отримуємо
\[f_{ave} \approx \dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{n}=\dfrac{f(x^∗_1)+f(x^∗_2)+⋯+f(x^∗_n)}{\left(\dfrac{b−a}{Δx}\right)}. \nonumber \]
Слідом за алгеброю чисельник - це сума, яка представлена як\(\sum_{i=1}^nf(x∗i),\) і ми ділимо на дріб. Щоб розділити на дріб, інвертуйте знаменник і помножте. Таким чином, приблизне значення для середнього значення функції задається
\[\dfrac{\sum_{i=1}^nf(x^∗_i)}{\left(\dfrac{b−a}{Δx}\right)}=\left(\dfrac{Δx}{b−a}\right)\sum_{i=1}^nf(x^∗_i)=\left(\dfrac{1}{b−a}\right)\sum_{i=1}^nf(x^∗_i)Δx. \nonumber \]
Це сума Рімана. Потім, щоб отримати точне середнє значення, візьміть межу, як\(n\) йде до нескінченності. Таким чином, середнє значення функції задається
\[\dfrac{1}{b−a}\lim_{n→∞}\sum_{i=1}^nf(x_i)Δx=\dfrac{1}{b−a}∫^b_af(x)dx. \nonumber \]
\(f(x)\)Дозволяти бути безперервним протягом інтервалу\([a,b]\). Потім середнє значення функції\(f(x)\) (або\(f_{ave}\)) on\([a,b]\) задається
\[f_{ave}=\dfrac{1}{b−a}∫^b_af(x)\,dx. \label{averagevalue} \]
Знайти середнє значення\(f(x)=x+1\) за інтервал\([0,5].\)
Рішення
Спочатку наведіть графік функції на заявленому інтервалі, як показано на малюнку\(\PageIndex{10}\).
![Графік в одному квадранті показує затінену область під функцією f (x) = x + 1 над [0,5].](https://math.libretexts.org/@api/deki/files/12427/5.2.7.png)
Область - це трапеція, що лежить на боці, тому ми можемо використовувати формулу площі для трапеції,\(A=\dfrac{1}{2}h(a+b),\) де\(h\) представляє висоту,\(a\) і\(b\) представляти дві паралельні сторони. Потім,
\(\displaystyle ∫^5_0x+1\,dx=\dfrac{1}{2}h(a+b)=\dfrac{1}{2}⋅5⋅(1+6)=\dfrac{35}{2}\).
Таким чином, середнє значення функції
\(\displaystyle \dfrac{1}{5−0}∫^5_0x+1\,dx=\dfrac{1}{5}⋅\dfrac{35}{2}=\dfrac{7}{2}\).
Знайти середнє значення\(f(x)=6−2x\) за інтервал\([0,3].\)
- Підказка
-
Використовуйте формулу середнього значення (Equation\ ref {averagevalue}) та використовуйте геометрію для оцінки інтеграла.
- Відповідь
-
\(3\)
Ключові поняття
- Певний інтеграл може бути використаний для обчислення чистої підписаної площі, яка є площею над\(x\) -віссю менше площі нижче\(x\) -осі. Чистий знак області може бути позитивним, негативним або нульовим.
- Складовими частинами визначеного інтеграла є integrand, змінна інтеграції та межі інтеграції.
- Неперервні функції на замкнутому інтервалі інтегруються. Функції, які не є безперервними, все ще можуть бути інтегрованими, залежно від характеру розривів.
- Властивості певних інтегралів можуть бути використані для оцінки інтегралів.
- Площа під кривою багатьох функцій можна обчислити за допомогою геометричних формул.
- Середнє значення функції можна обчислити за допомогою певних інтегралів.
Ключові рівняння
- Певний інтеграл
\(\displaystyle∫^b_af(x)\,dx=\lim_{n→∞}\sum_{i=1}^nf(x^∗_i)Δx\)
- Властивості визначеного інтеграла
\(\displaystyle∫^a_af(x)\,dx=0\)
\(\displaystyle∫^a_bf(x)\,dx=−∫^b_af(x)\,dx\)
\(\displaystyle∫^b_a[f(x)+g(x)]\,dx=∫^b_af(x)\,dx+∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_a[f(x)−g(x)]\,dx=∫^b_af(x)\,dx−∫^b_ag(x)\,dx\)
\(\displaystyle∫^b_acf(x)\,dx=c∫^b_af(x)\,dx\), для постійних\(c\)
\(\displaystyle∫^b_af(x)\,dx=∫^c_af(x)\,dx+∫^b_cf(x)\,dx\)
Глосарій
- середнє значення функції
- (Або\(f_{ave})\) середнє значення функції на інтервалі можна знайти, обчисливши певний інтеграл функції і розділивши це значення на довжину інтервалу
- певний інтеграл
- первинна операція числення; площа між кривою і\(x\) -віссю через заданий інтервал є певним інтегралом
- інтегрується функція
- функція інтегрується, якщо існує межа, що визначає інтеграл; іншими словами, якщо межа сум Рімана, що\(n\) йде до нескінченності, існує
- цілісний
- функція праворуч від символу інтеграції; integrand включає функцію інтегрується
- межі інтеграції
- ці значення з'являються у верхній і нижній частині знака інтеграла і визначають інтервал, через який повинна бути інтегрована функція
- чиста підписана область
- площа між функцією та\(x\) -віссю така, що площа нижче\(x\) -осі віднімається від області над\(x\) -віссю; результат такий же, як певний інтеграл функції
- загальна площа
- загальна площа між функцією та\(x\) -віссю обчислюється шляхом додавання площі над\(x\) -віссю та площі нижче\(x\) -осі; результат такий же, як певний інтеграл абсолютного значення функції
- змінна інтеграції
- вказує, яку змінну ви інтегруєте щодо; якщо вона є\(x\), то функція в integrand слідує\(dx\)
