Skip to main content
LibreTexts - Ukrayinska

9.1: Площа під кривою

  1. Last updated
  2. Save as PDF
  • Page ID
    54348

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Розрахунок площі під пряму можна проводити за допомогою геометрії. Розрахунок площі під кривою лінією вимагає обчислення. Часто площа під кривою може бути інтерпретована як накопичена кількість будь-якої функції моделювання. Припустимо, швидкість автомобіля в метрах в секунду може бути змодельована квадратичним за перші 8 секунд розгону:

    \[ s(t)=t^2 \nonumber\]

    Як далеко автомобіль проїхав за 8 секунд?

    Пошук площі під кривою

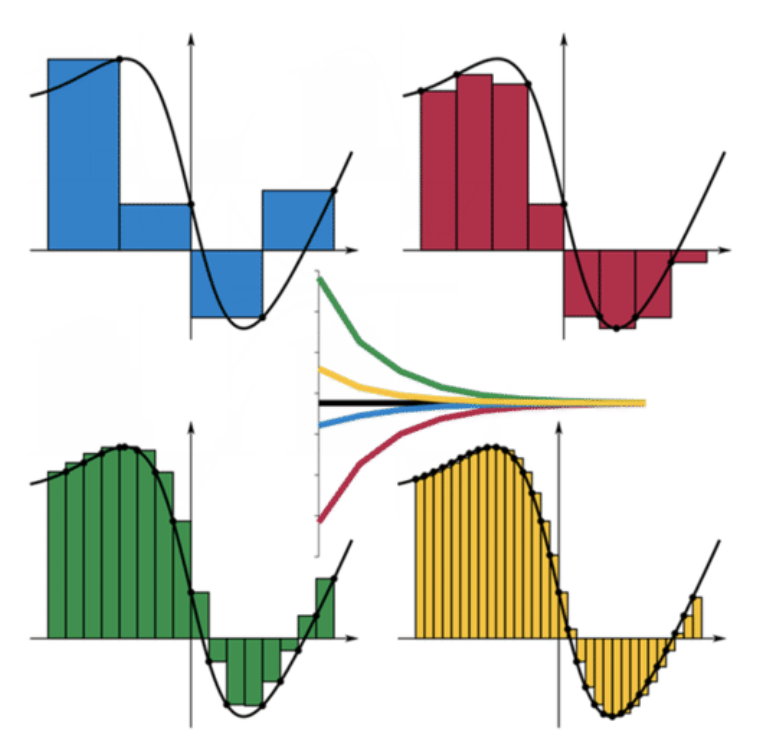
    Площа під кривою може бути апроксимована прямокутниками, однаково розташованими під кривою, як показано нижче. Для узгодженості ви можете вибрати, чи повинні поля потрапляти на криву в лівому куті, правому куті, максимальному значенні або мінімальному значенні. Чим більше ящиків ви використовуєте, тим вужчими будуть коробки і, таким чином, тим точніше буде ваше наближення площі.

    Знімок екрана 2021-01-20 о 7.35.08 PM.png

    КУБ.СМ ПО-СА

    Субінтервали створюються, коли інтервал розбивається на менші, однаково величини інтервали. Синє наближення використовує праві коробки для висоти кожного підінтервалу. Червоне наближення призначає висоті поля мінімальним значенням функції в кожному підінтервалі. Зелене наближення призначає висоті поля максимальним значенням функції в кожному підінтервалі. У жовтому наближенні використовуються ліві коробки. Прямокутники над віссю x матимуть позитивну площу, а прямокутники нижче осі x матимуть негативну площу у цьому контексті.

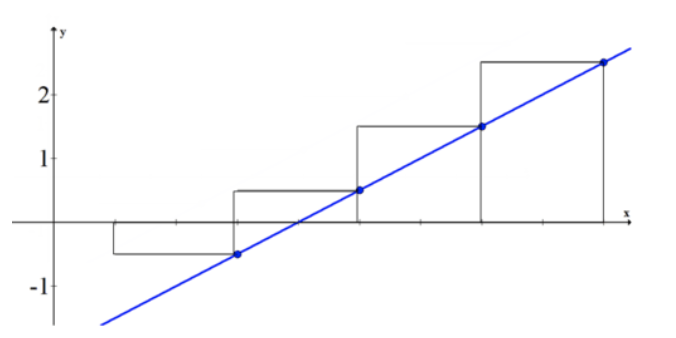
    Використання квадратів для оцінки площі під кривою називається Сумою Рімана. Візьмемо функцію f (x) =12x−2. Щоб обчислити суму Рімана (площа під кривою) між 1 та 9 функцією, спочатку намалюйте графік та поля.

    Знімок екрана 2021-01-20 о 7.36.55 PM.png

    https://commons.wikimedia.org/wiki/F...onvergence.png - CC BY-SA

    Площа першого ящика в 2 рази перевищує висоту функції, оціненої в 3:

    \[ 2⋅(\frac{1}{2}⋅3−2)=3−4=−1 \nonumber\]

    Оскільки ця коробка знаходиться під віссю x, його площа негативна.

    Площа для кожного з решти ящиків в 2 рази перевищує висоту функції, оціненої на 5, 7 і 9.

    \[ 2⋅(\frac{1}{2}⋅5−2)=5−4=1 \nonumber\]

    \[ 2⋅(\frac{1}{2}⋅7−2)=7−4=3 \nonumber\]

    \[ 2⋅(\frac{1}{2}⋅9−2)=9−4=5 \nonumber\]

    Приблизна сума загальної площі під кривою становить: −1+1+3+5=8 квадратних одиниць.

    Усі чотири наближення площі, показані раніше, покращуються, оскільки кількість ящиків збільшується. Насправді межа кожного наближення, коли кількість підінтервалів (коробок) збільшується до нескінченності, є точною площею під кривою.

    Тут приходить ідея числення інтеграла. Інтеграл - це межа суми, оскільки кількість доданих збільшується до нескінченності. Дозвіл - це одна з багатьох частин, які підсумовуються разом.

    \[ \int f(x)= \lim_{n \to ∞} \sum_{i=1}^n (\mbox{ Area of box i }) \nonumber\]

    Символ зліва є символом числення інтеграла.

    Приклади

    Приклад 1

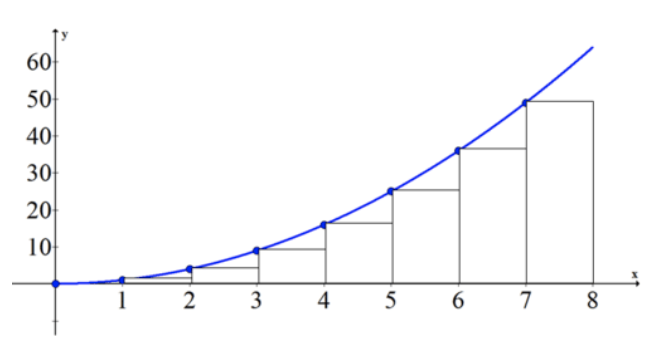
    Раніше вас попросили визначити, як далеко проїжджає машина за 8 секунд. Ви можете використовувати площу під кривою, щоб знайти загальну відстань, пройдену за перші 8 секунд. Оскільки квадратична крива, ви повинні вибрати кількість підінтервалів, які ви хочете використовувати, і чи потрібні праві або ліві поля для оцінки. Припустимо, ви вибрали 8 лівих коробок шириною один.

    Знімок екрана 2021-01-21 о 3.31.40 PM.png

    КУБ.СМ ПО-СА

    х 0 1 2 3 4 5 6 7
    Площа коробки праворуч 1⋅0 1⋅1 1⋅4 1⋅9 1⋅16 1⋅25 1⋅36 1⋅49

    Приблизна сума - 1+4+9+16+25+36+49=140. Це означає, що автомобіль проїхав приблизно 140 метрів за перші 8 секунд.

    Приклад 2

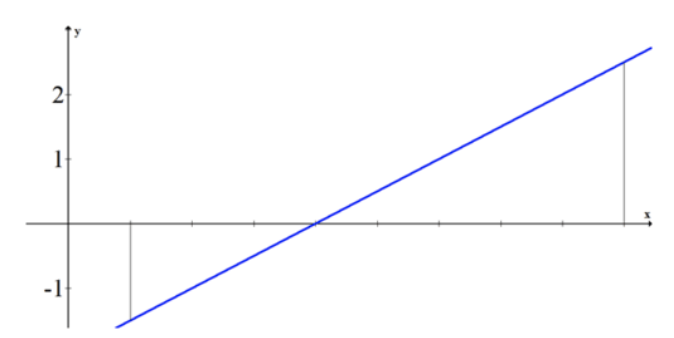
    Оцініть точну площу під використовуваною раніше кривою\( f(x)=\frac{1}{2}x−2 \nonumber\), використовуючи формулу площі для трикутника.

    Пам'ятайте, що область під віссю x є від'ємною, тоді як область над віссю x позитивна.

    Знімок екрана 2021-01-22 о 8.04.02 PM.png

    КУБ.СМ ПО-СА

    Негативна область:\( \frac{1}{2}⋅3⋅1.5=\frac{9}{4} \nonumber\)

    Позитивна область:\( \frac{1}{2}⋅5⋅2.5=\frac{25}{4} \nonumber\)

    Площа під кривою між 1 і 8:\( \frac{25}{4}−\frac{9}{4}=\frac{16}{4}=4 \nonumber\)

    Якщо порівняти цю відповідь з наближенням раніше, виявляється, що наближення шириною 2 одиниці виробляють площу зі значною похибкою.

    Приклад 3

    Логан подорожує на велосипеді зі швидкістю 20 миль/год протягом 3 годин. Потім вона сідає в машину і їздить 60 миль/год протягом 2 годин. Намалюйте як відстань проти часового графіка, так і швидкість проти часового графіка. Використовуйте область під аргументом кривої, щоб з'єднати два графіки.

    Відстань проти часу:

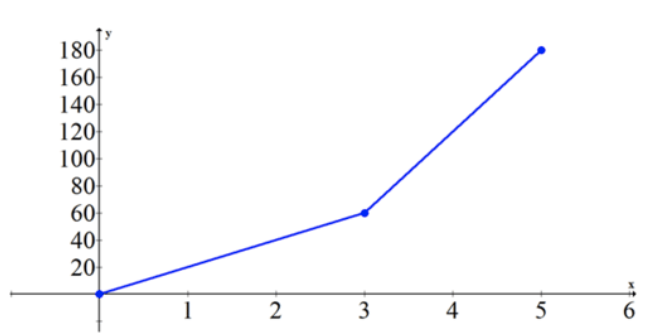
    Знімок екрана 2021-01-22 о 8.19.54 PM.png

    КУБ.СМ ПО-СА

    Ставка проти часу:

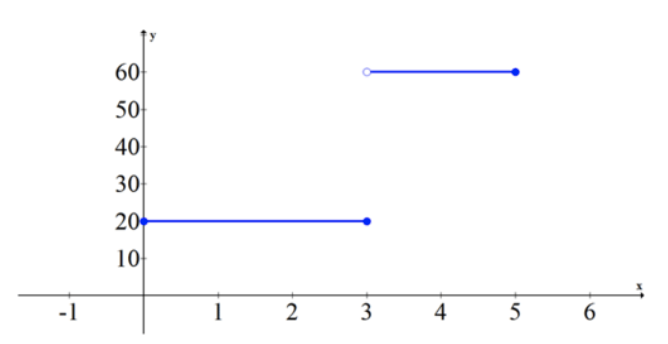
    Знімок екрана 2021-01-22 о 9.24.00 PM.png

    КУБ.СМ ПО-СА

    Нахил першого графа дорівнює 20 від 0 до 3, а потім 60 від 3 до 5. Другий графік - це графік нахилів з першого графа. Якщо обчислити площу другого графіка в ключових точках 0, 1, 2, 3, 4 і 5, ви побачите, що вони ідеально вирівнюються з точками на першому графіку.

    х Площа під кривою від 0 до x
    0 0
    1 20
    2 40
    3 60
    4 120
    5 180

    Приклад 4

    Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і праві кінцеві точки.

    \[ f(x)=3x^2−1, −1≤x≤7 \nonumber\]

    Хоча графік корисний для візуалізації проблеми, і малювання кожного поля може допомогти надати значення кожному резюме, це не завжди потрібно. Оскільки на загальному інтервалі −1≤x≤7 буде 8 підінтервалів, кожен інтервал матиме ширину 1. Висота кожного інтервалу буде знаходитися в правій кінцевій точці кожного підінтервалу (0, 1, 2, 3, 4, 5, 6, 7).

    \[ \sum height⋅width = \sum_{i=0}^{7}(3i^2−1)⋅1=412 \nonumber\]

    Приклад 5

    Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

    \[ f(x)=x^x, 1≤x≤3 \nonumber\]

    Коли кількість субінтервалів стане великим, а підінтервали стануть надзвичайно вузькими, намалювати точну картинку буде неможливо. Ось чому використання позначень підсумовування та продумування того, якими будуть індекси та аргумент, неймовірно важливо. З 20 субінтервалами між [1,3] кожен інтервал буде шириною 0,1. Ліва кінцева точка означає, що перше поле має висоту f (1), а друге поле має висоту f (1.1).

    \[ \sum height⋅width=f(1)⋅0.1+f(1.1)⋅0.1+f(1.2)⋅0.1+⋯+f(2.9)⋅0.1 \nonumber\]

    \[ =0.1(f(1)+f(1.1)+⋯f(2.9)) \nonumber\]

    \[ =0.1⋅\sum_{i=10}^{29}f(\frac{i}{10}) \nonumber\]

    \[ =0.1⋅\sum_{i=10}^{29} (\frac{i}{10})^{(\frac{i}{10})} \nonumber\]

    \[ ≈12.47144 \nonumber\]

    Ваш калькулятор може обчислити підсумовування, коли ви йдете в меню математики.

    Знімок екрана 2021-01-22 в 9.41.42 PM.png

    КУБ.СМ ПО-СА

     

    Рецензія

    1. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і праві кінцеві точки.

    \[ f(x)=x^2−x+1, 0≤x≤8 \nonumber\]

    2. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і ліві кінцеві точки.

    \[ f(x)=x^2−2x+1, −4≤x≤4 \nonumber\]

    3. Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

    \[ f(x)=\sqrt{x+3}, 0≤x≤4 \nonumber\]

    4. Орієнтуйте площу під кривою, використовуючи 100 субінтервалів і лівих кінцевих точок. Порівняйте з вашою відповіддю з #3.

    \[ f(x)=\sqrt{x+3}, 0≤x≤4 \nonumber\]

    5. Орієнтуйте площу під кривою, використовуючи вісім підінтервалів і ліві кінцеві точки.

    \[ f(x)=cos(x), 0≤x≤4 \nonumber\]

    6. Орієнтуйте площу під кривою, використовуючи двадцять субінтервалів і ліві кінцеві точки.

    \[ f(x)=cos(x), 0≤x≤4 \nonumber\]

    7. Орієнтуйте площу під кривою, використовуючи 100 субінтервалів і лівих кінцевих точок.

    \[ f(x)=cos(x), 0≤x≤4 \nonumber\]

    Наступний графік показує швидкість (у милі на годину) проти часу (у годині) для автомобіля.

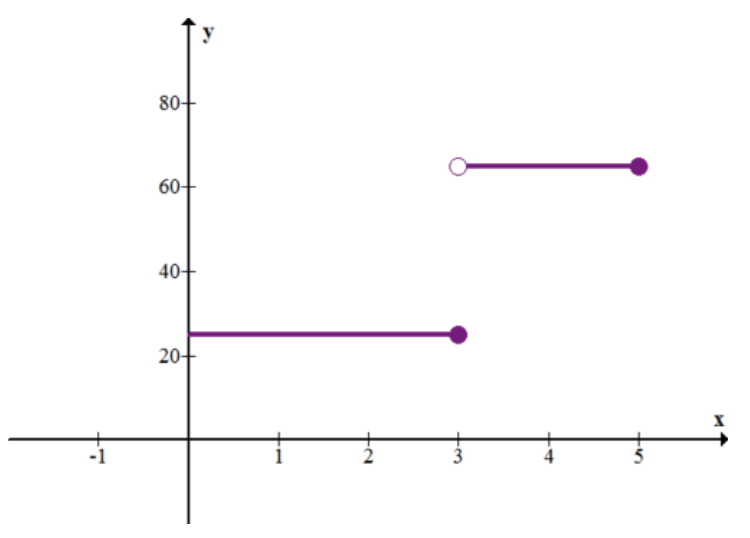
    Знімок екрана 2021-01-22 о 9.47.04 PM.png

    КУБ.СМ ПО-СА

    8. Опишіть, що відбувається з автомобілем.

    9. Як далеко проїхала машина за 5 годин?

    Наступний графік показує швидкість (у футах в секунду) проти часу (у секундах) для автомобіля.

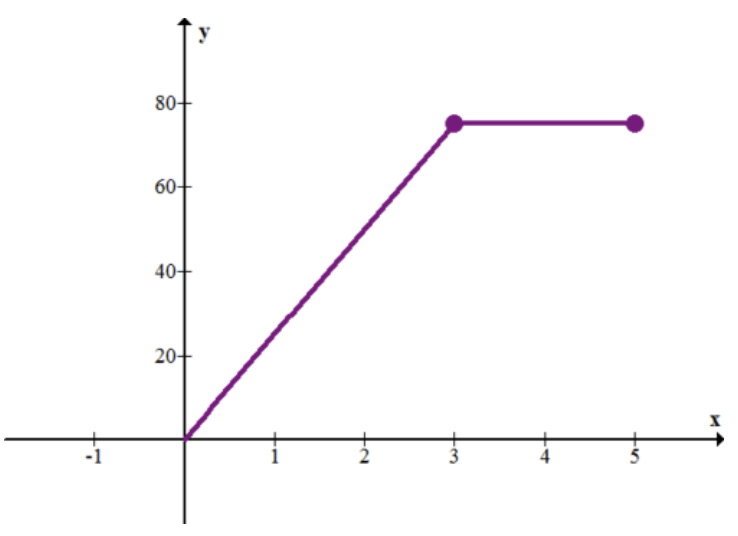
    Знімок екрана 2021-01-22 о 9.47.39 PM.png

    КУБ.СМ ПО-СА

    10. Опишіть, що відбувається з автомобілем. Зокрема, що відбувається в перші 3 секунди?

    11. Як далеко проїхала машина за 5 секунд?

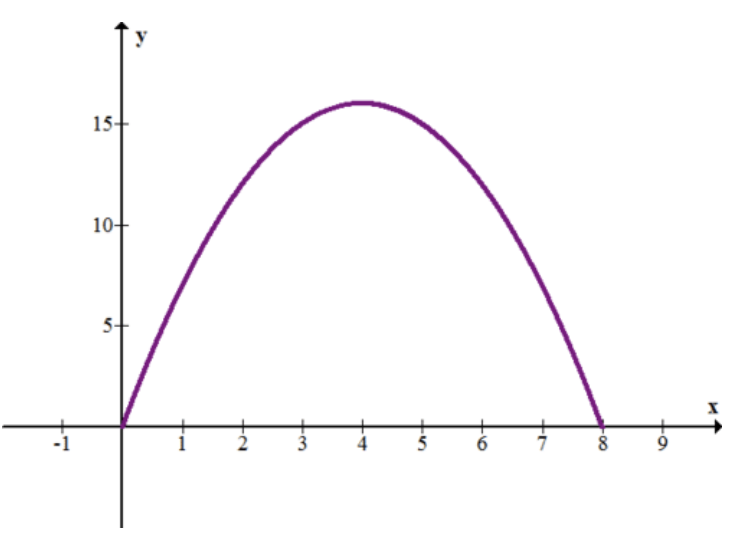
    На наступному графіку показано функцію f (x) =− (x−4) 2+16, яка представляє швидкість (у футах на секунду) проти часу (у секундах) для бігуна.

    Знімок екрана 2021-01-22 в 9.48.13 PM.png

    КУБ.СМ ПО-СА

    12. Опишіть, що відбувається з Раннер. Зокрема, що відбувається через 4 секунди?

    13. Використовуйте прямокутники, щоб наблизити загальну відстань (у футах), яку бігун пройшов за 8 секунд. Постарайтеся отримати якнайкраще наближення, наскільки це можливо.

    14. Поясніть, як інтеграл схожий на протилежність похідної.

    15. Як інтеграли співвідносяться з сумами?

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 14.9.

    Лексика

    Термін Визначення
    Δ Символ «Δ», читається «дельта», використовується для позначення «зміни в», як в «зміна швидкості з плином часу» =\( \frac{Δv}{t} \nonumber\).
    певний інтеграл Певний інтеграл дає площу між віссю x і кривою через певний інтервал.
    межа Межа - це значення, до якого наближається вихід функції, коли вхід функції наближається до заданого значення.
    субаінтервали Субінтервали створюються, коли інтервал розбивається на менші однаково величини інтервали.
    виклик Сума - це вираз, що підсумовується. Вона безпосередньо слідує за символом сигми.

    Додаткові ресурси

    Відео: Вступ до визначених інтегралів

    Практика: Площа під кривою