9.3: Суми площ
- Page ID
- 54347
Знаходження площі під кривою функції, f (x), є однією з центральних проблем, яка виникає в Обчислення. Ви вже знаєте, як обчислити площу деяких простих функцій кривих фігур за допомогою геометричних формул, і іноді можете швидко використовувати ці методи. Але, що б ви зробили, якби криві функції були більш складними? Ключовий підхід обчислення полягає в тому, щоб взяти простий метод, застосувати його в невеликому масштабі, а потім доводити до межі на нескінченності.
Щоб отримати деяке розуміння ідеї знаходження області під кривою, зробіть наступне, перш ніж йти далі: візьміть просту криву параболи (увігнуту вгору і позитивну), розділіть інтервал на осі x на кількість рівних підінтервалів і намалюйте прямокутник в кожному підінтервалі, який перетинає параболу. Підсумовування прямокутників буде оцінкою площі. Скільки різних типів перетинів може зробити прямокутник з параболою? Чи можете ви сказати що-небудь про те, як перетин під або над оцінює площу під кривою? Ви бачите, що чим більше прямокутників використовується для заданого інтервалу, тим краща оцінка?
Ріман Суми
Для простих функцій, таких як f (x) =c (c> 0) або f (x) =cx (c - константа > 0) протягом деякого інтервалу [0, x 0], ми можемо використовувати просту геометрію, щоб отримати площу під кожною кривою (спробуйте підтвердити це самостійно):
- Для f (x) = c (c> 0); область A - це область простого прямокутника, а = Cx0.
- Для f (x) = cx (c> 0); площа A - це площа простого трикутника,\( A=\frac{1}{2}x_0(cx_0)=c\frac{x_0^2}{2} \nonumber\).
Як можна визначити площу для більш складних функцій?
Розглянемо нашу основну квадратичну функцію\( f(x)=x^2 \nonumber\). Припустимо, нас цікавить знаходження площі, A, під кривою від x=0 до x=1. Площа, про яку ми говоримо, - це поперечно-штрихований простір під кривою, показаною нижче.
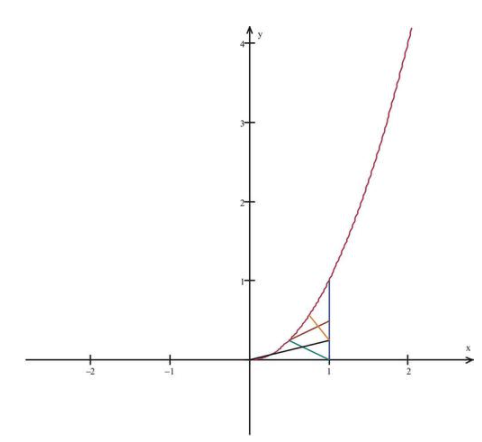
CC ЗА NC-SA
Один із способів оцінити площу під кривою - обчислити площу квадрата, який має кут в (1, 1), як показано нижче, а потім взяти половину.
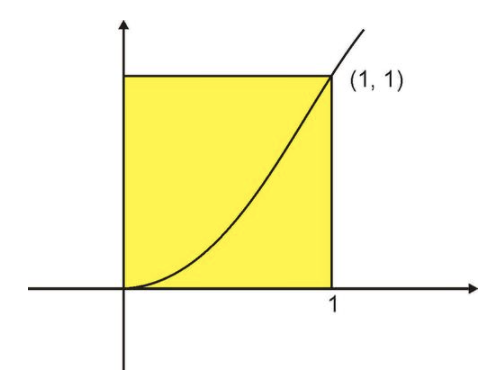
CC ЗА NC-SA
Це дає площу\( A=\frac{1}{2} \nonumber\). Це хороша перша оцінка області; точна відповідь буде показана\( A=\frac{1}{3} \nonumber\).
Як ми можемо зробити кращу оцінку? Як щодо поділу інтервалу x від x = 0 до x=1 на кілька підінтервалів однакової ширини.
Давайте розглянемо проблеми, кожна з яких має більше субінтервалів, ніж попередня.
4 рівні субінтервали:
Почніть з використання чотирьох таких субінтервалів, як зазначено:
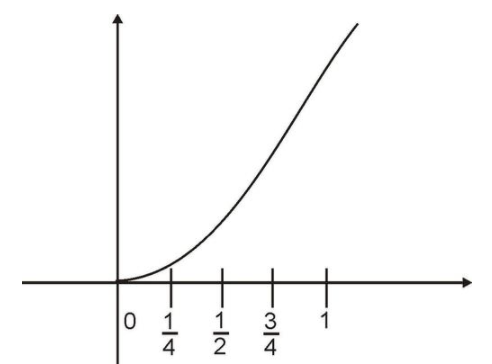
Тепер ми побудуємо чотири прямокутника, які послужать основою для нашого наближення площі. Підінтервали будуть служити шириною прямокутників. Ми візьмемо довжину кожного прямокутника максимальним значенням функції в підінтервалі. (Ми також могли б вибрати мінімальне або середнє значення функції в підінтервалі.)
Звідси ми отримуємо наступну цифру:
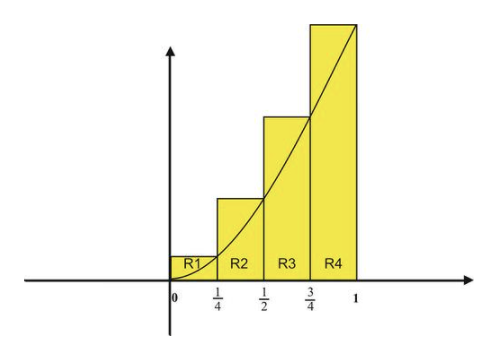
Якщо ми називаємо прямокутники R1−R4, зліва направо, то ми маємо області
Знаходження площі під кривою функції, f (x), є однією з центральних проблем, яка виникає в Обчислення. Ви вже знаєте, як обчислити площу деяких простих функцій кривих фігур за допомогою геометричних формул, і іноді можете швидко використовувати ці методи. Але, що б ви зробили, якби криві функції були більш складними? Ключовий підхід обчислення полягає в тому, щоб взяти простий метод, застосувати його в невеликому масштабі, а потім доводити до межі на нескінченності.
Щоб отримати деяке розуміння ідеї знаходження області під кривою, зробіть наступне, перш ніж йти далі: візьміть просту криву параболи (увігнуту вгору і позитивну), розділіть інтервал на осі x на кількість рівних підінтервалів і намалюйте прямокутник в кожному підінтервалі, який перетинає параболу. Підсумовування прямокутників буде оцінкою площі. Скільки різних типів перетинів може зробити прямокутник з параболою? Чи можете ви сказати що-небудь про те, як перетин під або над оцінює площу під кривою? Ви бачите, що чим більше прямокутників використовується для заданого інтервалу, тим краща оцінка?
8 Рівні суб-інтервали:
Якщо розділити інтервал на 8 рівних підінтервалів, ширина кожного прямокутника тепер w=18.
Оцінкою площі тепер стає:
\[ A≈R_1+R_2+R_3+R_4+R_5+R_6+R_7+R_8 \nonumber\]
\[ ≈ \sum_{i=1}^8 R_i \nonumber\]Використання сигма-нотації
\[ ≈\frac{1}{512}+\frac{4}{512}+\frac{9}{512}+\frac{16}{512}+\frac{25}{512}+\frac{36}{512}+\frac{49}{512}+\frac{64}{512} \nonumber\]
\[ ≈\frac{204}{512} \nonumber\]
\[ A≈0.3984 \nonumber\]
Зверніть увагу, що\( (\sum_{i=1}^8 R_i) \nonumber\) використане вище позначення сигми дозволяє нам вказувати суму окремих ділянок прямокутника без необхідності виписувати всі окремі терміни. Символ сигми з цими індексами говорить нам, як позначаються прямокутники і скільки членів в сумі.
Крім того, підсумовування прямокутників, що дає наближення площі, можна записати в наступному загальному вигляді:
\[ A≈R=\sum_{i=1}^n R_i= \sum_{i=1}^n f(w_i)(x_i−x_{i−1})=\sum_{i=1}^n f(w_i)Δx_i \nonumber\]
де ми вибираємо значення n, щоб бути таким великим, як ми хочемо, wi бути будь-яким значенням x в інтервалі\( (x_i−x_i−1)\nonumber\), і\( (x_i−x_i−1) \nonumber\) бути i-м з n підінтервалів (не обов'язково рівних) в інтервалі [a, b], на якому визначено f. Цей тип підсумовування називається сумою Рімана.
16 рівних підінтервалів:
Якщо ми тепер розділимо інтервал на 16 рівних підінтервалів, ширина кожного прямокутника тепер\( w=\frac{1}{16} \nonumber\).
Оцінкою площі тепер стає:
\[ A≈R_1+R_2+R_3+R_4+R_5+⋯+R_{16} \nonumber\]
\[ ≈\sum_{i=1}^{16} R_i \nonumber\]Використання сигма-нотації
\[ ≈\frac{1}{4096}+\frac{4}{4096}+\frac{9}{4096}+⋯+\frac{196}{4096}+\frac{225}{4096}+\frac{256}{4096} \nonumber\]
\[ ≈\frac{1496}{4096} \nonumber\]
\[ A≈0.3652 \nonumber\]
Знову ж таки, сигма-позначення було використано для усунення необхідності виписувати всі окремі терміни.
Таблиця дає зведення результатів оцінки площі до цих пір.
|
Суб-інтервали |
Оцінка площі |
|
1 |
1 (0.5) |
|
4 |
0,4688 |
|
8 |
0,3984 |
|
16 |
0,3652 |
Інтуїтивно ми маємо відчуття, що ми можемо покращити наближення площі, розділивши інтервал від x = 0 до x = 1 на все більше і більше підінтервалів, створюючи таким чином послідовно менші та менші прямокутники для уточнення наших оцінок.
Тепер ми готові формалізувати використання сум для обчислення площ.
Спочатку визначаємо нижню і верхню суми:
Нехай f - обмежена функція в замкнутому інтервалі [a, b] і\( P=[x_0,…,x_n] \nonumber\) поділ [a, b] на n підінтервалів.
Визначте нижню і верхню суми, відповідно, над розділом P,
\[ S(P)=\sum_{1}^{n} m_i(x_i−x_{i−1})=m_1(x_1−x_0)+m_2(x_2−x_1)++m_n(x_n−x_{n−1}) \nonumber\]
\[ T(P)= \sum_1^n M_i(x_i−x_{i−1})=M1_(x_1−x_0)+M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\]
де mi - мінімальне значення f в інтервалі довжини\( x_i−x_{i−1} \nonumber\) і\( M_i \nonumber\) максимальне значення f в інтервалі довжини\( x_i−x_{i−1} \nonumber\).
S (P) та T (P) - це суми Рімана, де mi та Mi є особливим вибором для wi у загальній формулюванні суми Рімана вище.
Далі ми зв'яжемо область під кривою з межею нижньої або верхньої сум для все більшої кількості субінтервалів:
Дозволяти f — неперервна невід'ємна функція на замкнутому інтервалі [a, b]. Нехай P є розділом n рівних підінтервалів над [a, b]. Тоді площа під кривою f - межа верхньої і нижньої сум, тобто
\[ A= \lim_{n \to +∞} S(P)= \lim_{n \to +∞}T(P) \nonumber\]
Наступна проблема показує, як ми можемо використовувати ці визначення для пошуку області під кривою.
Показати, що межа верхньої суми для функції\( f(x)=x^2 \nonumber\), від\( x=0 \mbox{ to } x=x_0 \nonumber\), наближається до значення\( A=\frac{x_0^3}{3} \nonumber\).
Нехай P є розділом n рівних підінтервалів над\( [0,x_0] \nonumber\). За визначенням ми маємо
\[ T(P)= \sum{1}^{n} M_i(x_i−x_{i−1})=M_1(x_1−x_0)+M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\]
Кожен прямокутник матиме ширину\( \frac{x_0}{n} \nonumber\), так що оцінка T (P) дорівнює:\( T(P)= \sum_{1}^{n} M_i(x_i−x_{i−1}) \nonumber\)
\( = M_2(x_2−x_1)+…+M_n(x_n−x_{n−1}) \nonumber\)
\( =(\frac{x_0}{n})2\frac{x_0}{n}+(2\frac{x_0}{n})2\frac{x_0}{n}+…+(n\frac{x_0}{n})2\frac{x_0}{n} \nonumber\)Рівна довжина суб-інтервалів.
\( =(\frac{x_0}{n})^2\frac{x_0}{n}(1^2+2^2+3^2+…+n^2) \nonumber\)
\( =(\frac{x_0}{n})^3(1^2+2^2+3^2+…+n^2) \nonumber\)
\( =(\frac{x_0^3}{n})^3(\frac{n(n+1)(2n+1)}{6}) \nonumber\)Використовує:\( \sum_{i=1}^{n} i^2=\frac{n(n+1)(2n+1)}{6} \nonumber\)
\( =(\frac{x_0^3}{6})(\frac{n(n+1)(2n+1)}{n^3}) \nonumber\)
\(=(\frac{x_0^3}{6})(1+\frac{1}{n})(2+\frac{1}{n}) \nonumber\)
Зауважте, що:
\[ \lim_{n \to ∞} [(\frac{x_0^3}{6})(1+\frac{1}{n})(2+\frac{1}{n})]=(\frac{x_0^3}{6})⋅2=\frac{x_0^3}{3} \nonumber\]
Площа, A, під кривою функції\( f(x)=x^2 \nonumber\) від\( x=0 \mbox{ to } x=x_0 \nonumber\), наближається до значення\( A=\frac{x_0^3}{3} \nonumber\). Зверніть увагу, що якщо x0=1, то отримаємо результат A=13. Порівняйте це значення з результатами попередньої проблеми.
Такий же підхід для визначення площі можна використовувати і з S (P), і він дає той же результат,\( A = \frac{x_0^3}{3} \nonumber\).
Приклади
Приклад 1
Раніше вас запитали про використання прямокутників для оцінки площі під кривою. Скільки різних типів перетинів може зробити прямокутник з параболою? Чи можете ви сказати що-небудь про те, як перетин під або над оцінює площу під кривою? Чи бачите ви, що чим більше прямокутників використовується (менший підінтервал) для заданого інтервалу, тим краща оцінка площі?
Там, де ваш прямокутник перетинає параболу, встановлює висоту прямокутника, і просто залежить від значення x в межах підінтервалу: лівий кінець прямокутника (початок підінтервалу), правий кінець прямокутника (кінець підінтервалу) або десь між ними. Для цієї увігнутої параболи ви повинні бути в змозі побачити, що використання лівого прямокутника занижує площу під параболою; правий прямокутник завищує площу. Прямокутник з висотою десь посередині, скажімо, в середині, може переоцінити частину і недооцінити частину, тобто забезпечити кращу оцінку площі.
Приклад 2
Скористайтеся визначенням межі області, щоб знайти площу за функцією f (x) =4−x від 1 до x=3.
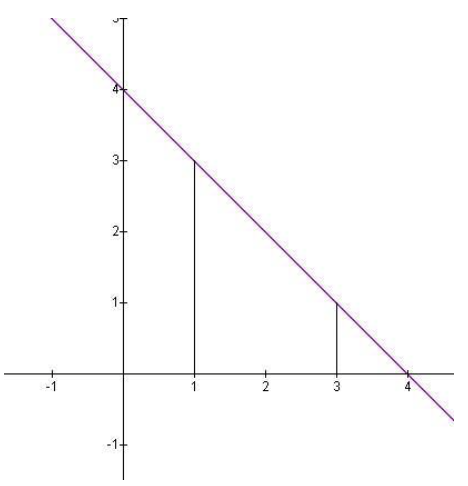
Якщо розділити інтервал [1,3] на n рівних підінтервалів, то кожен підінтервал матиме довжину\( \frac{3−1}{n}=\frac{2}{n} \nonumber\), а висота 3−i△ x, оскільки i варіюється від 1 до n.\( △x=\frac{2}{n} \nonumber\)
\( S(P)= \sum_1^n m_i(x_i−x_{i−1}) \nonumber\)Нижня сума, використовуючи мінімальне значення функції в кожному підінтервалі.
\( = \sum_1^n (3−i\frac{2}{n})\frac{2}{n} \nonumber\)
\( S(P)= \sum_1^n m_i(x_i−x_{i−1}) \nonumber\)Піб-інтервали однакової довжини.
\( = \sum_1^n (3⋅\frac{2}{n})− \sum_1^n i(\frac{2}{n})^2 \nonumber\)
\( =6−(\frac{2}{n})^2 \sum_1^n i \nonumber\)
\( =6−(\frac{2}{n})^2⋅(\frac{n(n+1)}{2}) \nonumber\)Використовує:
\( =6−2⋅(\frac{n(n+1)}{n^2}) \sum_{i=1}^n i=\frac{n(n+1)}{2} \nonumber\)
\( S(P)=6−2⋅(1+\frac{1}{n}) \nonumber\)
Зауважте, що:
\[ \lim_{n \to ∞} [6−2⋅(1+\frac{1}{n})]=6−2=4 \nonumber\]
Площа, A, під кривою функції наближається до значення A=4. Такий же підхід можна використовувати і з S (P), даючи той же результат.
Звичайно, цей приклад також може бути вирішений за допомогою простої геометрії. Це залишається читачеві, щоб підтвердити, що два методи дають однакову площу.
Рецензія
Для #1 -3 знайдіть S (P) і T (P) під розділом P.
- \( f(x)=1−x^2, P={0,12,1,32,2} \nonumber\)
- \( f(x)=2x^2, P={−1,−12,0,12,1} \nonumber\)
- \( f(x)=\frac{1}{x}, P={−4,−3,−2,−1} \nonumber\)
- Розглянемо f (x) =2−x від x=0 до x=2. Використовуйте суми Рімана з чотирма підінтервалами однакових довжин. Виберіть середні точки кожного підінтервалу в якості вибіркових точок.
- Повторіть задачу #1 за допомогою геометрії для обчислення точної площі області під графіком f (x) =2−x від x=0 до x=2. (Підказка: Намалюйте графік області та подивіться, чи можна обчислити її площу за допомогою формул вимірювання площі з геометрії.)
- Повторіть задачу #4 за допомогою визначення певного інтеграла для обчислення точної площі області під графом f (x) =2−x від x=0 до x=2.
- \( f(x)=x^2−x \nonumber\)від x=1 до x=4. Використовуйте суми Рімана з п'ятьма підінтервалами рівних довжин. Виберіть ліву кінцеву точку кожного підінтервалу як точки вибірки.
- Повторіть задачу #7, використовуючи визначення певного інтергаля для обчислення точної площі області під графом\( f(x)=x^2−x \nonumber\) від x=1 до x=4.
- Розглянемо\( f(x)=3x^2 \nonumber\). Обчислити суму Рімана f на [0, 1] під кожною з наступних ситуацій. У кожному конкретному випадку використовуйте праву кінцеву точку в якості вибіркових точок.
- Два підінтервала однакової довжини.
- П'ять підінтервалів однакової довжини.
- Десять підінтервалів однакової довжини.
- Виходячи з ваших відповідей вище, спробуйте вгадати точну площу під графіком f на [0, 1].
- Розглянемо\( f(x)=e^x \nonumber\). Обчислити суму Рімана f на [0, 1] під кожною з наступних ситуацій. У кожному конкретному випадку використовуйте праву кінцеву точку в якості вибіркових точок.
- Два підінтервала однакової довжини.
- П'ять підінтервалів однакової довжини.
- Десять підінтервалів однакової довжини.
- Виходячи з ваших відповідей вище, спробуйте вгадати точну площу під графіком f на [0, 1].
- Знайти площу мережі під графом\( f(x)=x^3−x \nonumber\); x=−1 до x=1. (Підказка: Намалюйте графік і перевірте симетрію.)
- Знайдіть загальну площу, обмежену графіком\( f(x)=x^3−x \nonumber\) та віссю x, від x=−1 до x=1.
- Використовуйте свої знання геометрії, щоб оцінити певний інтеграл:\( \int\limits_0^3 \sqrt{9−x^2}dx \nonumber\)
(Підказка: встановіть\( y= \sqrt{9−x^2} \nonumber\) і вирівняйте обидві сторони, щоб побачити, чи можете ви розпізнати область за геометрією.)
Для #14 -15 знайдіть площу під кривою, використовуючи граничне визначення площі.
- f (x) = 3х+5 від х=2 до х=6.
- \( f(x)=x^2 \nonumber\)від x=1 до x=3.
Огляд (Відповіді)
Щоб переглянути відповіді на рецензування, відкрийте цей PDF-файл і знайдіть розділ 5.4.
Лексика
| Термін | Визначення |
|---|---|
| обмежена функція | Обмежена функція - це функція f (x), для якої f (x) ≤M (M дійсне число) для всіх значень x у домені. |
| нижча сума | Нижня сума - це сума Рімана, яка обирає мінімальне значення функції на кожному підінтервалі у розділі замкнутого інтервалу. |
| поділ замкнутого інтервалу | Розділ замкнутого інтервалу - це розкладання всього інтервалу на ряд суміжних підінтервалів. |
| сигма-позначення | Позначення сигми також відоме як підсумовування позначення і є способом представлення суми чисел. Це особливо корисно, коли цифри мають певну закономірність або буде потрібно занадто багато часу, щоб виписати без абревіатури. |
| верхня сума | Верхня сума - це сума Рімана, яка обирає максимальне значення функції на кожному підінтервалі у розділі замкнутого інтервалу. |
Додаткові ресурси
PLIX - Грайте, вчіться, взаємодійте, досліджуйте: Суми площ: Оцінка за допомогою прямокутників
Відео: Трапецієподібне наближення площі під кривою
Практика: Суми площ
Реальний світ: Дзвонивши його в