Skip to main content
LibreTexts - Ukrayinska

8.2: Метод Ньютона

  1. Last updated
  2. Save as PDF
  • Page ID
    54375

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Ми хочемо подивитися на пошук коренів многочлена. Іноді многочлен не може бути легко врахований, а інші алгебраїчні методи (наприклад, квадратне рівняння) непридатні або не працюють. Зіткнувшись з математичною задачею, яку неможливо вирішити простими алгебраїчними засобами, обчислення іноді забезпечує спосіб пошуку наближених розв'язків.

    Метод Ньютона

    Простий приклад допоможе ввести Метод Ньютона для наближення коренів поліноміального рівняння.

    Припустимо, ви хочете обчислити\( \sqrt{5} \nonumber\) без використання калькулятора або таблиці. Будь-які ідеї, як це можна зробити? Спробуйте подумати про цю проблему по-іншому, щоб ви використовували лінеаризацію.

    Припустимо, що нас цікавить розв'язування квадратного рівняння:

    \[ f(x)=x^2−5=0 \nonumber\]

    Ми знаємо, що це рівняння має коріння\( x=± \sqrt{5} \nonumber\).

    Ідея полягає в тому, щоб знайти лінеаризацію f (x) у відповідній точці, а потім розв'язати лінійне рівняння для x. Це доданий поворот до задачі лінеаризації!

    Як вибрати точку лінеаризації? Так як\( \sqrt{4}<\sqrt{5}<\sqrt{9} \nonumber\), це означає\( 2<\sqrt{5}<3 \nonumber\).

    Ми вибираємо лінійне наближення f (x), щоб бути поруч\( x_0=2 \nonumber\) (але, також\( x_0=3 \nonumber\) може бути вибрано).

    \[ f(x)=x^2−5 \mbox{ and } f(2)=−1 \nonumber\]

    \[ f′(x)=2x \mbox{ and } f′(2)=4 \nonumber\]

    Використовуючи формулу лінійного наближення,

    \[ f(x)≈f(x_0)+f′(x_0)(x−x_0) \nonumber\]

    \[ ≈−1+(4)(x−2) \nonumber\]

    \[ ≈−1+4x−8 \nonumber\]

    \[ ≈4x−9 \nonumber\]

    Зверніть увагу, що це рівняння набагато легше вирішити, ніж\( f(x)=x^2−5=0 \nonumber\).

    Встановлюючи f (x) =0 і вирішуючи для x, отримаємо,

    \[ 4x−9=0 \nonumber\]

    \[ x=\frac{9}{4} \nonumber\]

    \[ =2.25 \nonumber\]

    Це досить гарне наближення, оскільки калькулятор дасть x = 2.23607, нижче на 0,014. Ми можемо насправді зробити це наближення до кореня f (x) ще краще, повторюючи те, що ми тільки що зробили, але використовуючи останню оцінку\( x_1=2.25= \frac{9}{4} \nonumber\), число, яке ще ближче до фактичного значення\( \sqrt{5} \nonumber\).

    \[ f(x)=x^2−5 \mbox{ and } f(2.25)=\frac{1}{16} \nonumber\]

    \[ f′(x)=2x \mbox{ and } f′(2)= \frac{9}{2} \nonumber\]

    Використовуючи знову лінійне наближення,

    \[ f(x)≈f(x_1)+f′(x_1)(x−x_1) \nonumber\]

    \[ ≈ \frac{1}{16}+\frac{9}{2}(x−\frac{9}{4}) \nonumber\]

    \[ ≈\frac{9}{2}x−\frac{161}{16} \nonumber\].

    Розв'язуючи для x, встановивши f (x) =0, отримаємо

    \[ x=x_2=\frac{161}{72}=2.23611 \nonumber\]

    що є ще кращим наближенням, ніж\[ x_1=\frac{9}{4} \nonumber\].

    Ми могли б продовжити цей процес, створюючи краще наближення до\( \sqrt{5} \nonumber\), як показано в таблиці, де остання оцінка наближає правильну відповідь до 5 місць. Слава богу за калькулятори!

    п

    \( x_n \nonumber\)

    \( f(x_n) \nonumber\)

    \( f′(x-n) \nonumber\)

    \( \frac{f(x_n)}{f′(x_n)} \nonumber\)

    \( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\)

    1

    2

    -1

    4

    -0.25

    2.25

    2

    2.25

    0.0625

    4.5

    0.01389

    2.23611

    3

    2.23611

    0.00019

    4.47222

    0,00004

    2.23607

    4

    2.23607

    —

    —

    —

    —

    Це основна ідея методу Ньютона. Ось короткий виклад методу:

    1. З огляду на функцію f (x), знайдіть f′ (x).
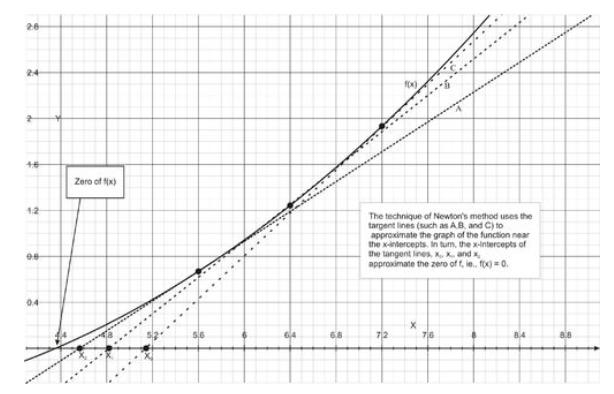
    2. Оцініть перше наближення, x 0, до розв'язку рівняння f (x) =0. Використовуйте графік, який допоможе знайти перше наближення при необхідності (див. Малюнок нижче).
    3. Використовуйте поточне наближення x n, щоб знайти наступне наближення, x n +1, за допомогою рекурсійного відношення.

    \[ x_{n+1}=x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\].

    1. Повторюйте попередній крок до тих пір, поки не відбудеться потрібний рівень зближення.

    Зверніть увагу, що в деяких випадках метод Ньютона не сходиться.

    Знімок екрана 2021-01-07 о 1.04.48 PM.png

    CC ЗА NC-SA

    Приклади

    Приклад 1

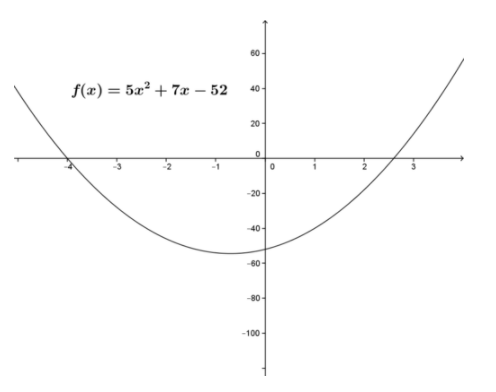
    Порівняйте розв'язки f (x) =5x2+7x−52 в інтервалі [2, 3] за допомогою квадратичної формули та методу Ньютона.

    Функція показана на малюнку.

    Для f (x) =5x2+7x−52=0 використання квадратичної формули дає точний розв'язок x=2.6 у інтервалі.

    Знімок екрана 2021-01-07 о 1.05.36 PM.png

    CC ЗА NC-SA

    Використання методу Ньютона з початковою оцінкою x 0 =3 дає результати, наведені в таблиці.

    п

    \( x_n \nonumber\)

    \( f(x_n) \nonumber\)

    \( f′(x-n) \nonumber\)

    \( \frac{f(x_n)}{f′(x_n)} \nonumber\)

    \( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\)

    1

    3

    14

    37

    0,3784

    2.6216

    2

    2.6216

    0,7151

    33.216

    0.0215

    2.6001

    3

    2.6001

    0,0033

    33.001

    0,0001

    2.6000

    4

    2.6000

    —

    —

    —

    —

    Техніка стрімко сходиться до розчину.

    Приклад 2

    Використовуйте метод Ньютона, щоб знайти коріння многочлена\( f(x)=x^3+x−1 \nonumber\).

    Завдання полягає в розв'язанні рівняння\( f(x)=x^3+x−1=0 \nonumber\).

    Рівняння, які нам потрібні, такі:

    \[ f(x)=x^3+x−1 \nonumber\]

    \[ f′(x)=3x^2+1 \nonumber\].

    Використовуючи рекурсійну зв'язок,

    \[ x_{n+1}=x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\]

    \[ =x_n−\frac{x^3_n+x_n−1}{3x^2_n+1} \nonumber\].

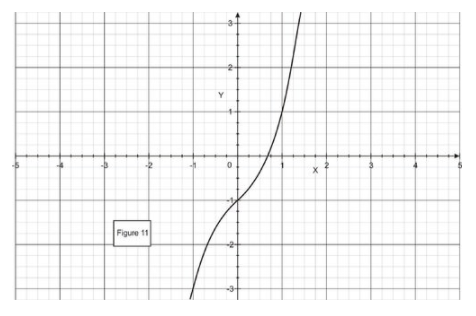
    Щоб допомогти нам знайти перше наближення, складаємо графік f (x). Як випливає з малюнка, безліч\( x_1=0.6 \nonumber\).

    Знімок екрана 2021-01-07 в 1.26.08 PM.png

    CC ЗА NC-SA

    Потім, використовуючи рекурсію, ми можемо генерувати x1:

    \[ x_{n+1}=x_n−\frac{x^3_n+x_n−1}{3x^2_n+1} \nonumber\]

    \[ x_2=0.6−\frac{(0.6)^3+(0.6)−1}{3(0.6)^2+1} \nonumber\]

    \[ =0.6884615 \nonumber\].

    Використовуючи рекурсійне відношення кілька разів, ми можемо знайти x3 та x4, як показано в таблиці.

    п

    \( x_n \nonumber\)

    \( f(x_n) \nonumber\)

    \( f′(x-n) \nonumber\)

    \( \frac{f(x_n)}{f′(x_n)} \nonumber\)

    \( x_n−\frac{f(x_n)}{f′(x_n)} \nonumber\)

    1

    0.6

    -0.184

    2.08

    -0.084615

    0.6884615

    2

    0.6884615

    0.01477796

    2.42 19377

    0,0061017

    0.6823598

    3

    0.6823598

    0.00007669

    2.3968445

    0.0000320

    0.6823278

    4

    0.6823278

    —

    —

    —

    —

    Робимо висновок, що розв'язання рівняння\[ x^3+x−1=0 \nonumber\] становить близько 0,6823.

    Приклад 3

    Використовуйте метод Ньютона, щоб показати, щоб знайти корінь\( f(x)=cos(2x)−x \nonumber\).

    Рівняння, які нам потрібні, такі:

    \( f(x)=cos(2x)−x \nonumber\)

    \( f(x)=−2sin(2x)−1 \nonumber\)

    Використовуючи рекурсійну зв'язок,

    x_ {n+1} = x_n\ розрив {f (x_n)} {f′ (x_n)}\ номер\)

    \( =x_n−\frac{cos(2x_n)−x_n}{−2sin(2x_n)−1} \nonumber\)

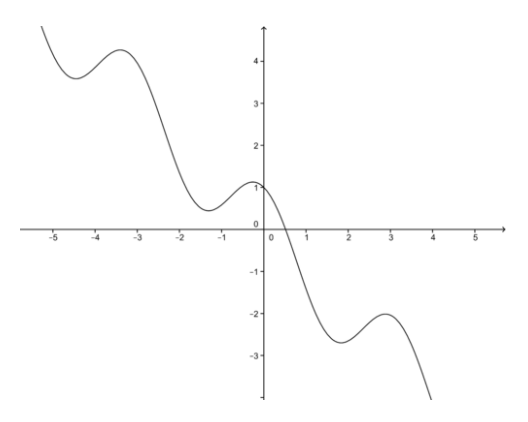
    Щоб допомогти нам знайти перше наближення, складаємо графік f (x). Як підказує цифра, встановіть першу оцінку на рівні 0,5.

    Знімок екрана 2021-01-08 о 10.49.52 AM.png

    CC ЗА NC-SA

    Використання рекурсійного відношення кілька разів дає значення таблиці:

    п

    \( x_n \nonumber\)

    \( f(x_n) \nonumber\)

    \( \frac{f(x_n)}{f′(xn)} \nonumber\)

    1

    0.500000

    0.0403023

    -0.015216_8

    2

    0.515022

    -0.0002400

    0.0000884

    3

    0.5 14933

    -0.0000000

    0.0000000

    4

    0.5 14933

    —

    —

    Зроблено висновок, що розв'язком рівняння cos (2x) −x=0 є 0,514933.

    Рецензія

    Для всіх проблем використовуйте метод Ньютона, щоб знайти коріння.

    1. \( x^3+3=0 \nonumber\).
    2. \( −x+3\sqrt{−1+x}=0 \nonumber\).
    3. \( 4x^2−x−2 \mbox{ in the interval } [-1, 0] \nonumber\).
    4. \( 4x^3−6x^2−1 \nonumber\).
    5. \( 5e^{−x}+x^3 \nonumber\).
    6. \( cosx−x \nonumber\).
    7. \( x^5−7x^2+2 \mbox{ in the interval} [-1, 0] \nonumber\).
    8. \( x^5−7x^2+2 \mbox{ in the interval } [0, 1] \nonumber\).
    9. \( x^2cosx−x \mbox{ in the interval } [4, 5] \nonumber\).
    10. \( x^2cosx−x \mbox{ in the interval } [7, 8] \nonumber\).
    11. \( f(x)=x−2sin(x) \mbox{ to five decimal places, starting with initial guess } x_0=3 \nonumber\).
    12. \( f(x)=6x^3−4x+1 \nonumber\)до трьох знаків після коми, починаючи з початкової здогадки\( x_0=1.2 \nonumber\).
    13. \( f(x)=ln(x)×(ln(x)+4)+1 \nonumber\)до п'яти знаків після коми, починаючи з початкової здогадки\( x_0=1 \nonumber\).
    14. \( f(x)=tan(x)−csc(x) \nonumber\)до шести цифр точності, починаючи з початкового вгадування\( x_0=0.7 \nonumber\).
    15. \( f(x)=tan^{−1}(x)+cos(x) \nonumber\)до чотирьох цифр точності, починаючи з початкового вгадування\( x_0=−2 \nonumber\).

    Огляд (Відповіді)

    Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 4.11.

    Лексика

    Термін Визначення
    метод Ньютона Метод Ньютона є ітераційною процедурою обчислення кореня рівняння.

    Додаткові ресурси

    PLIX: Грайте, вчіться, взаємодійте, досліджуйте - метод Ньютона

    Відео: Метод Ньютона для розв'язання рівнянь

    Практика: Метод Ньютона

    Реальний світ: Як дістатися до кореня речей