2.16: Докази паралелограма

Last updated
Save as PDF

Page ID: 54520

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Застосуйте теореми, щоб показати, чи чотирикутник має дві пари паралельних сторін.

Чотирикутники, які є паралелограмами

Нагадаємо, що паралелограм - це чотирикутник з двома парами паралельних сторін. Навіть якщо чотирикутник не позначений з двома парами сторін, це все одно може бути паралелограмом. Нижче наведено список теорем, які допоможуть вам вирішити, чи є чотирикутник паралелограмом чи ні.

1. Зворотна теорема протилежних сторін: Якщо обидві пари протилежних сторін чотирикутника конгруентні, то фігура є паралелограмом.

Якщо

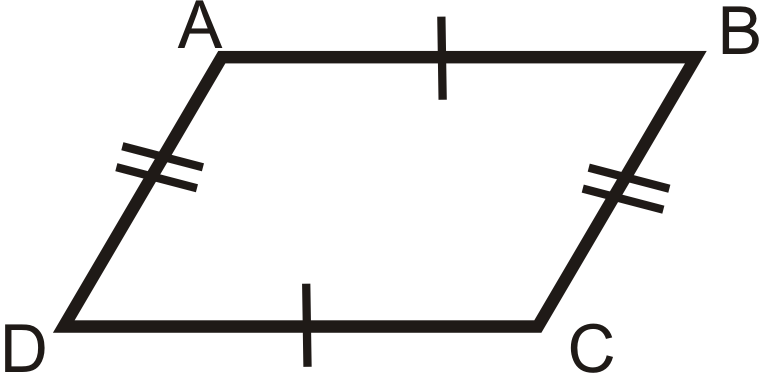
F-д_Б44Ф3Ф753 АЕ5Д2С0Ф64 Фе 05А 27747 Е73Е8409Е7А42А40EBE4A1B+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

потім

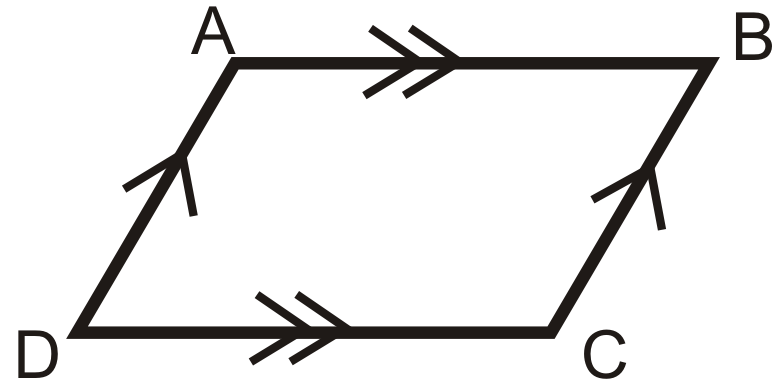
F-д_994д6497 ЦБА Е0Е45С57ДАА 4Д03Е 6067Е99015ДФ4ДФ 97С8БФ5А14596+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

2. Протилежні кути Теорема Конверс: Якщо обидві пари протилежних кутів чотирикутника конгруентні, то фігура є паралелограмом.

Якщо

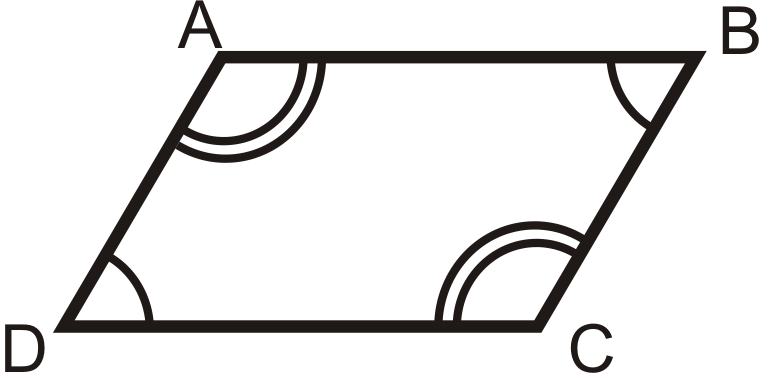
Ф-д_2118168440Ф8Ф8Ф1 А13С1238 ЕФ26д6ФА54С1173ФБ4Е4Е2А20С7199C+зображення_крихіткий+зображення_крихіткий_крошечкою.PNG — Малюнок\(\PageIndex{3}\)

потім

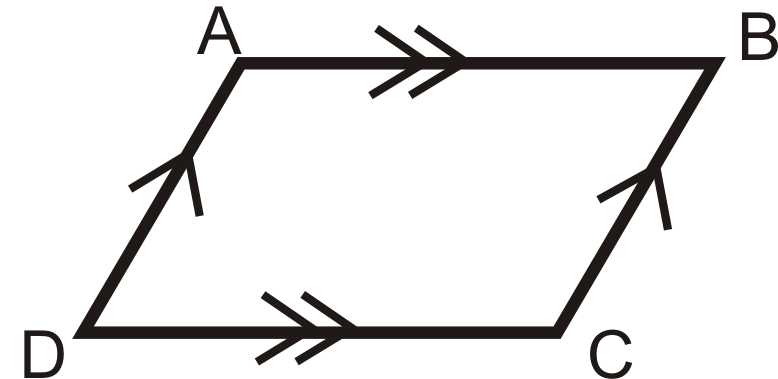
F-D_528830801800A01007e868c589b2Ebf40ab26919F4557be5e5E605481A+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{4}\)

3. Теорема діагоналей паралелограма Converse: Якщо діагоналі чотирикутника бісектують один одного, то фігура є паралелограмом.

Якщо

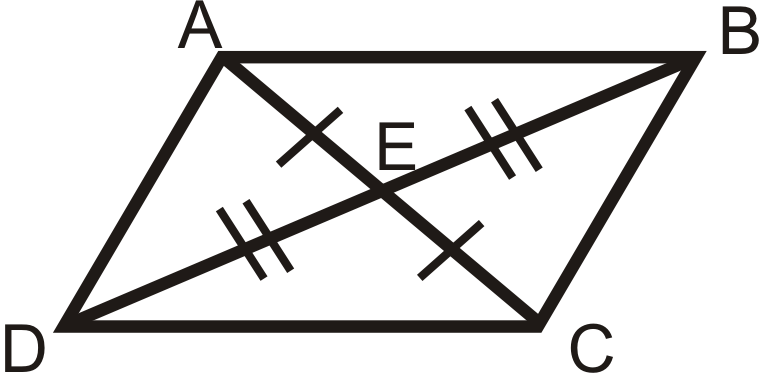
F-D_46C004C44А75296D2ААС 72БД737291 БАЕ01 АБ65Е18204Ф3586ЦА+зображення_крихіткий+зображення_крихітка_крихіткий.PNG — Малюнок\(\PageIndex{5}\)

потім

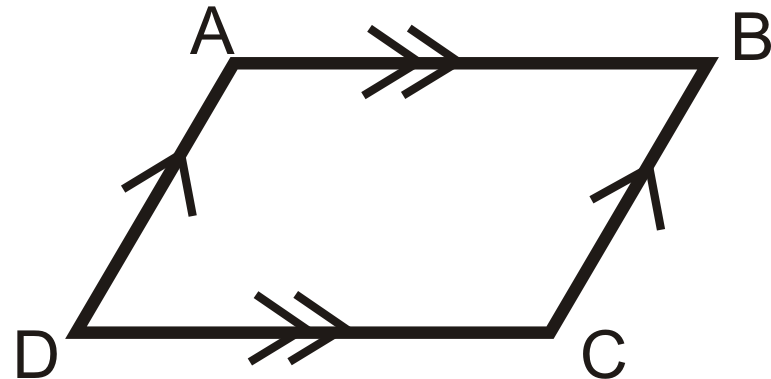
Ф-Д_С6443Е1С10КФ2Е9С4Д75БА 5Б555Б815Д0А23Е976А0Б40Е5Ф+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{6}\)

4. Теорема паралельних конгруентних сторін: Якщо чотирикутник має один набір паралельних ліній, які також є конгруентними, то це паралелограм.

Якщо

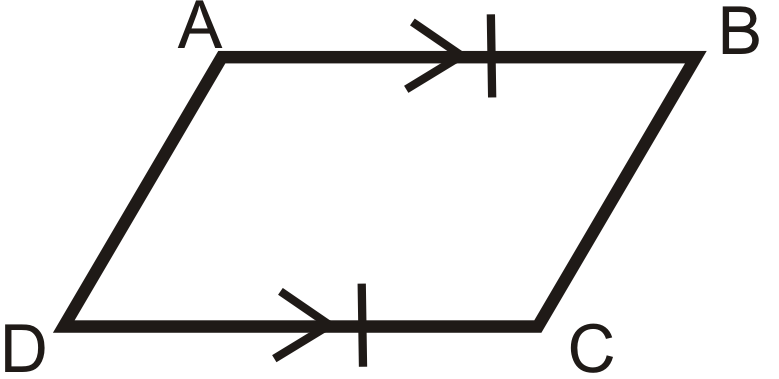
Ф-Д_Е46203Ф33А 4881541307Б95407Д5031345 ЕДСБ82АЕ45А0С3АА76+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{7}\)

потім

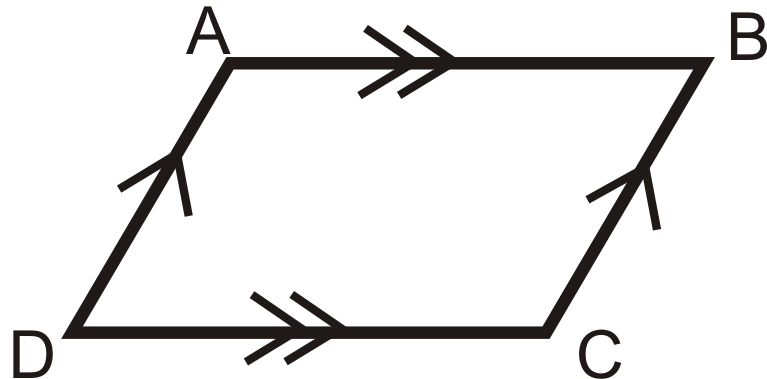
F-D_7D8FCF2 FeA2284750352C44 ФДД де 20ДБ6255Д6298Ф2Ф47BE907FF997+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{8}\)

Ви можете використовувати будь-яку з наведених вище теорем, щоб показати, що чотирикутник - це паралелограм. Якщо ви працюєте у площині x−y, вам може знадобитися знати наведені нижче формули, щоб допомогти вам скористатися теоремами.

Формула нахилу,\(\dfrac{y_2−y_1}{x_2−x_1}\). (Пам'ятайте, що якщо схили однакові, то лінії паралельні).
Формула відстані,\(\sqrt{(x_2−x_1)^2+(y_2−y_1)^2}\). (Це допоможе вам показати, що дві сторони є конгруентними).
Формула середньої точки,\( ( \dfrac{x_1+x_2}{2}, \dfrac{y_1+y_2}{2} )\). (Якщо середні точки діагоналей однакові, то діагоналі розділяють один одного).

Що робити, якщо вам дали чотири пари координат, які утворюють чотирикутник? Як ви могли визначити, чи цей чотирикутник є паралелограмом?

Приклад\(\PageIndex{1}\)

Доведіть теорему паралельних конгруентних сторін.

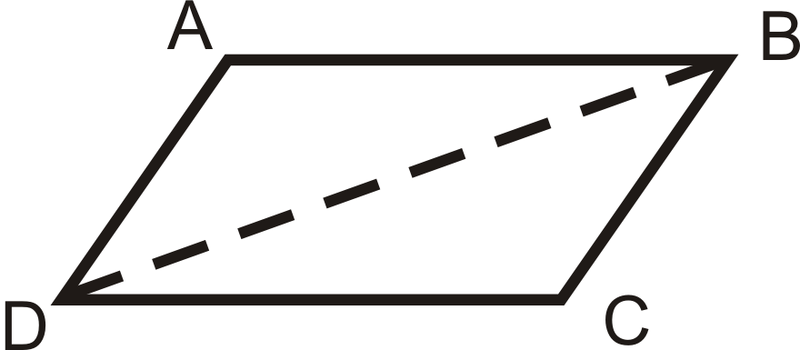
F-д_481247021БД 2921618 ЕДФ 2Ф5Е05543 ФФ7668412А6А797825Б7Б69Ф29+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{9}\)

Дано:\(\overline{AB}\parallel\overline{DC}\), і\(\overline{AB}\cong \overline{DC}\)

Доведіть:\(ABCD\) це паралелограм

Рішення

*Заява*	*Причина*
1. \(\overline{AB}\parallel\overline{DC}\), і\(\overline{AB}\cong \overline{DC}\)	1. Враховується
2. \(\angle ABD\cong \angle BDC\)	2. Альтернативні внутрішні кути
3. \(\overline{DB}\cong \overline{DB}\)	3. Рефлексивний\(PoC\)
4. \(\Delta ABD\cong \Delta CDB\)	4. САС
5. \(\overline{AD}\cong \overline{BC}\)\)	5. CPCTC
6. \(ABCD\)є паралелограмом	6. Протилежні сторони Converse

Приклад\(\PageIndex{2}\)

\(ABCD\)Яке значення\(x\) зробив би паралелограм?

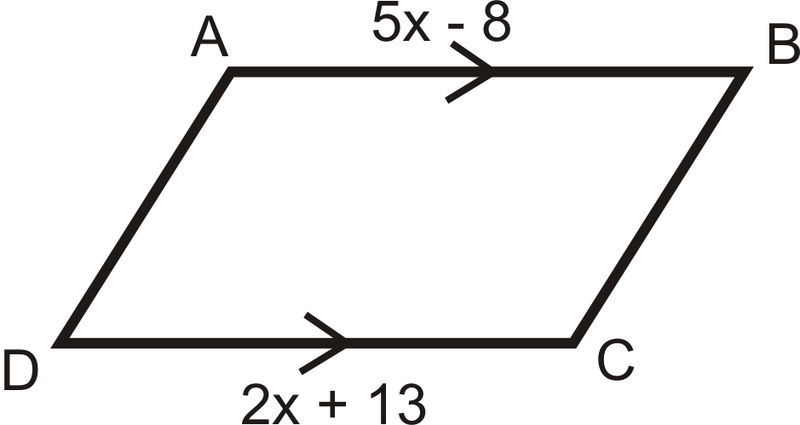
F-д_57бе 9d320081b376883ЕС8 САД8136 Дед Ф5Е1644Ф34Д20438C1632327+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{10}\)

Рішення

\(\overline{AB}\parallel\overline{DC}\). За теоремою паралельних конгруентних сторін,\(ABCD\) буде паралелограм, якщо\(AB=DC\).

\(\begin{align*} 5x−8 &=2x+13 \\ 3x &=21 \\ x &=7 \end{align*}\)

Приклад\(\PageIndex{3}\)

Доведіть зворотну теорему протилежних сторін.

З огляду на:\(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\)

Доведіть:\(ABCD\) це паралелограм

Рішення

*Заява*	*Причина*
1. \(\overline{AB}\cong \overline{DC}\),\(\overline{AD}\cong \overline{BC}\)	1. Дано
2. \(\overline{DB}\cong \overline{DB}\)	2. Рефлексивний\(PoC\)
3. \(\Delta ABD\cong \Delta CDB\)	3. ССС
4. \(\angle ABD\cong \angle BDC\),\(\angle ADB\cong \angle DBC\)	4. \(CPCTC\)
5. \(\overline{AB}\parallel\overline{DC}\),\(\overline{AD}\parallel\overline{BC}\)	5. Альтернативні внутрішні кути Converse
6. \(ABCD\)є паралелограмом	6. Визначення паралелограма

Приклад\(\PageIndex{4}\)

\(EFGH\)Чотирикутник - паралелограм? Звідки ти знаєш?

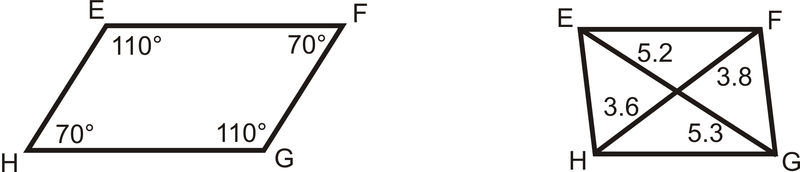
Ф-Д_Б1740Б63357С5Д41ФД536Ф61 АК 4336Се 081028133139Б46445Б5А7АФ+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{12}\)

Рішення

За теоремою протилежних кутів Converse,\(EFGH\) є паралелограмом.

\(EFGH\)не є паралелограмом, тому що діагоналі не розділяють один одного.

Приклад\(\PageIndex{5}\)

Чотирикутник\(ABCD\) є паралелограмом?

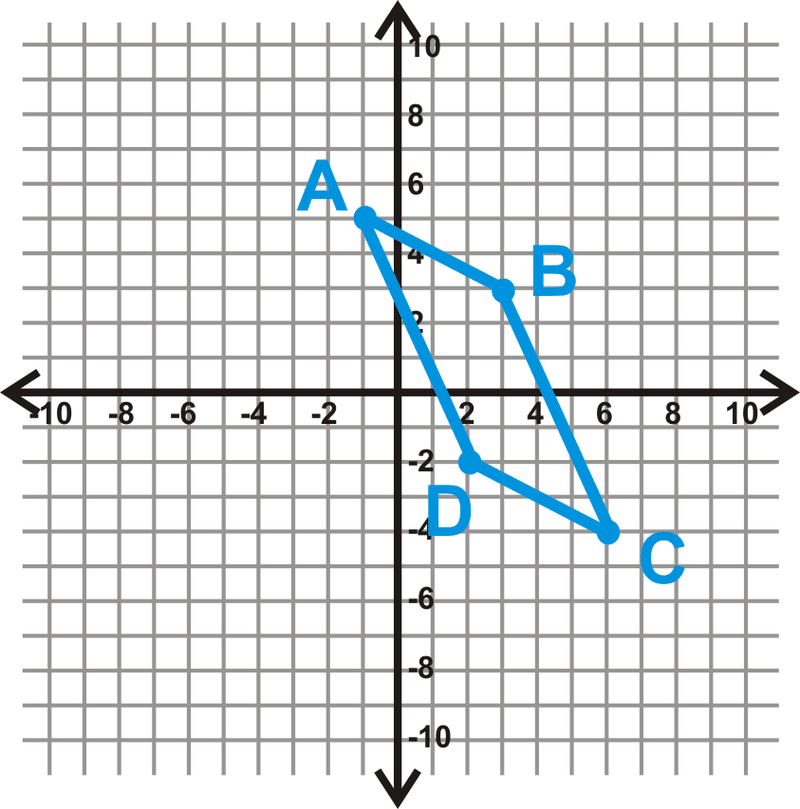
Ф-д_ад 6С14БК1Б86Д3ЕЕА А76 АЧБД 23277А9070ЕБД2С788ДЕА 374E53 BBC+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{13}\)

Рішення

Давайте використаємо теорему паралельних конгруентних сторін, щоб побачити, чи\(ABCD\) є паралелограмом. Спочатку знайдіть довжину AB і CD за допомогою формули відстані.

\(\begin{align*} AB &=\sqrt{(−1−3)^2+(5−3)^2} & CD &=\sqrt{(2−6)^2+(−2+4)^2} \\ &=\sqrt{(−4)^{2}+2^2} & &=\sqrt{(−4)^2+2^2} \\ &=\sqrt{16+4}=\sqrt{20} & & =\sqrt{16+4}=\sqrt{20} \end{align*}\)

Далі знайдіть ухили, щоб перевірити, чи паралельні лінії.

\(\begin{align*} Slope \: AB =\dfrac{5−3}{−1−3} =\dfrac{2}{−4} &=−\dfrac{1}{2} &Slope \: CD=\dfrac{−2+4}{2−6}=\dfrac{2}{−4}=−\dfrac{1}{2} \end{align*}\)

\(AB=CD\)а нахили однакові (маючи на увазі, що лінії паралельні),\(ABCD\) так і паралелограм.

Рецензія

З питань 1-12 визначте, чи є чотирикутники паралелограмами.

Малюнок\(\PageIndex{14}\)
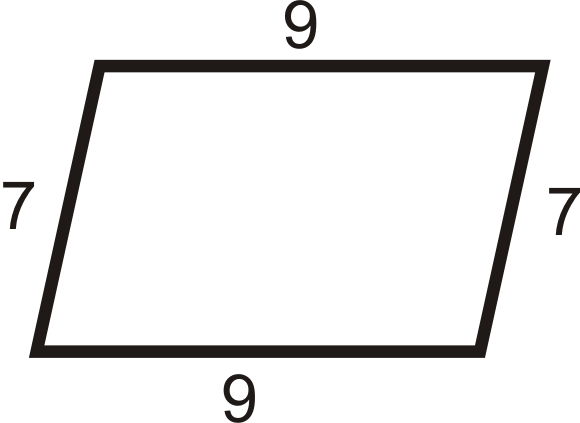
Малюнок\(\PageIndex{15}\)
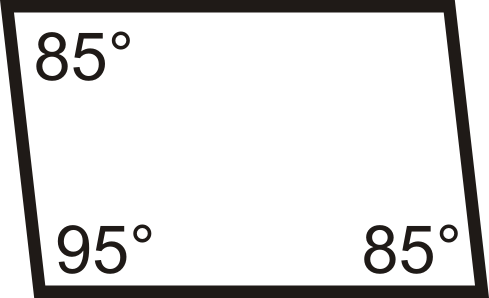
Малюнок\(\PageIndex{16}\)
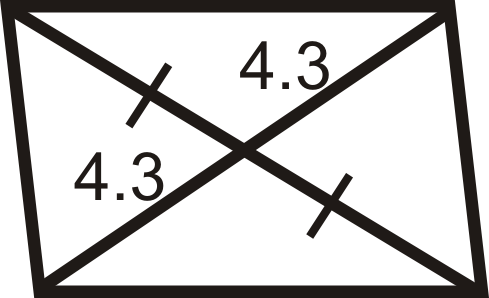
Малюнок\(\PageIndex{17}\)
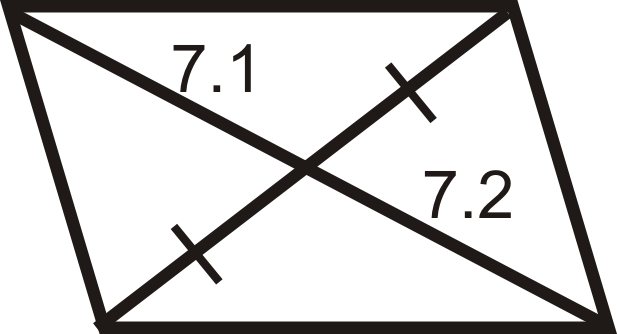
Малюнок\(\PageIndex{18}\)
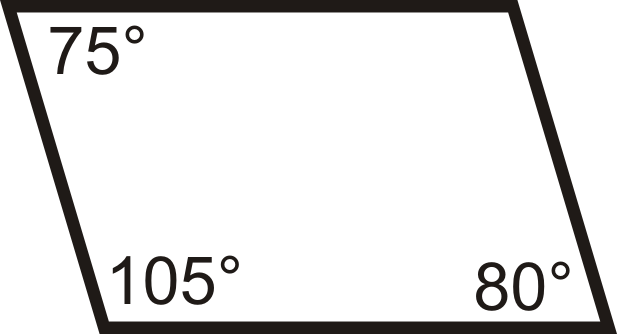
Малюнок\(\PageIndex{19}\)
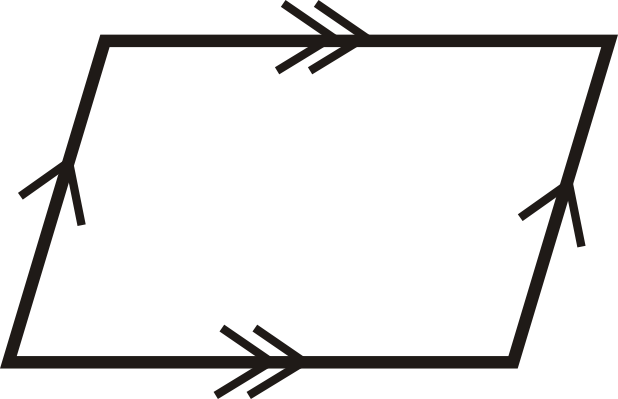
Малюнок\(\PageIndex{20}\)
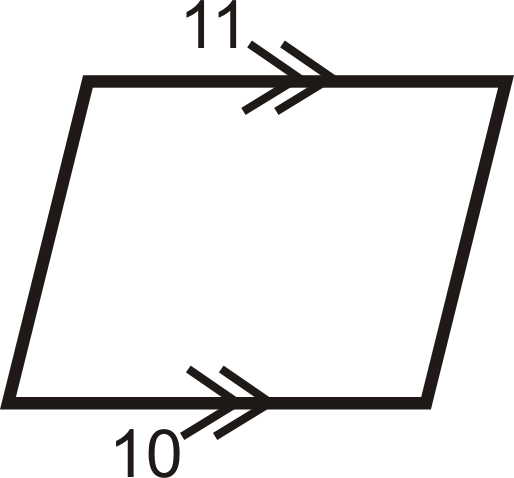
Малюнок\(\PageIndex{21}\)
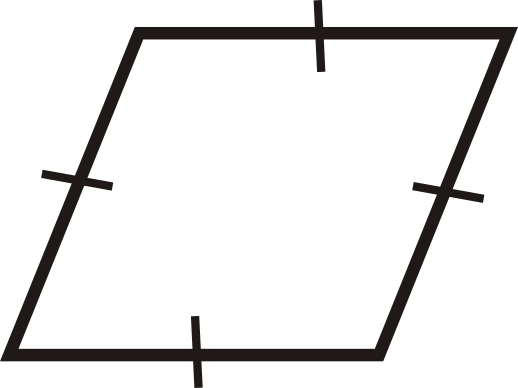
Малюнок\(\PageIndex{22}\)
Малюнок\(\PageIndex{23}\)
Малюнок\(\PageIndex{24}\)
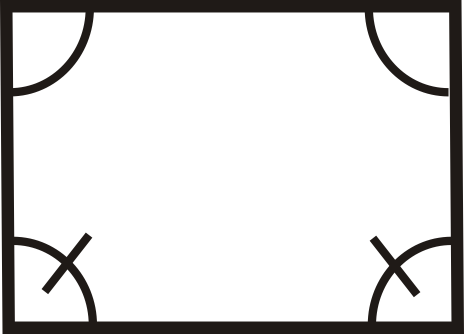
Малюнок\(\PageIndex{25}\)

Для питань 13-18, визначити значення\(x\) і\(y\) що б зробити чотирикутник паралелограм.

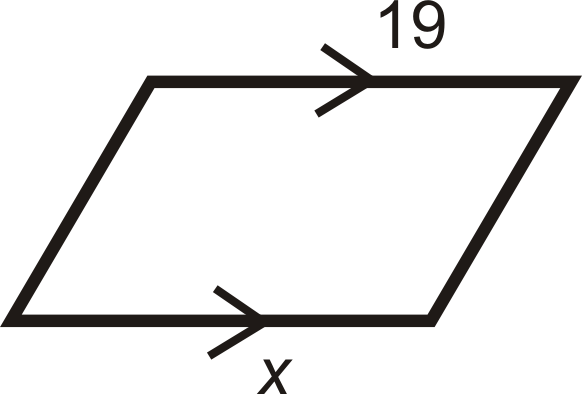
Малюнок\(\PageIndex{26}\)
Малюнок\(\PageIndex{27}\)
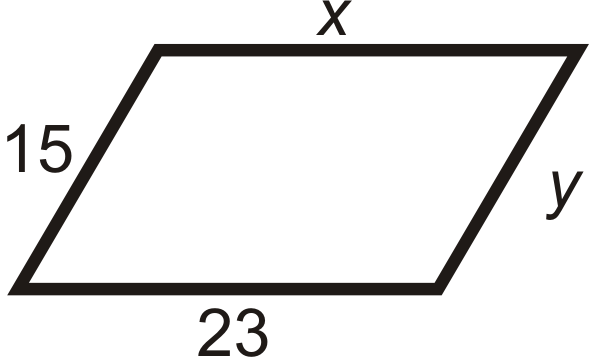
Малюнок\(\PageIndex{28}\)
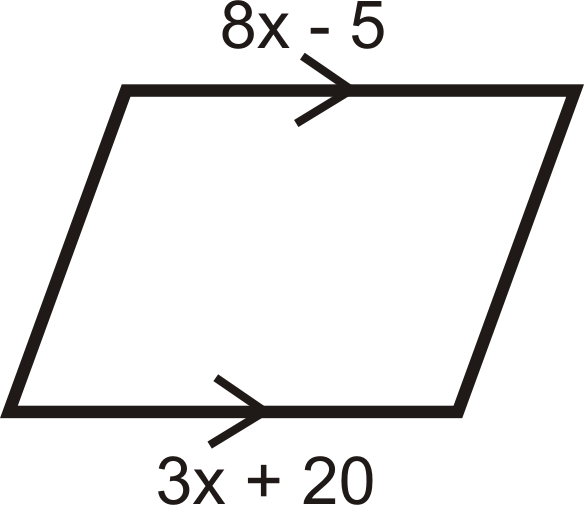
Малюнок\(\PageIndex{29}\)
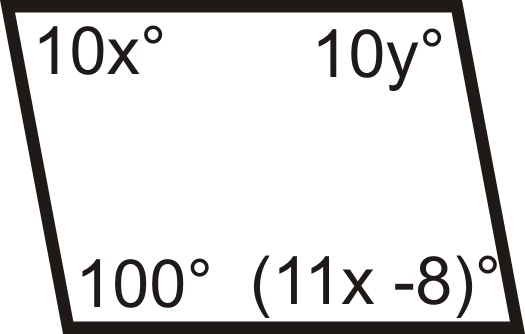
Малюнок\(\PageIndex{30}\)
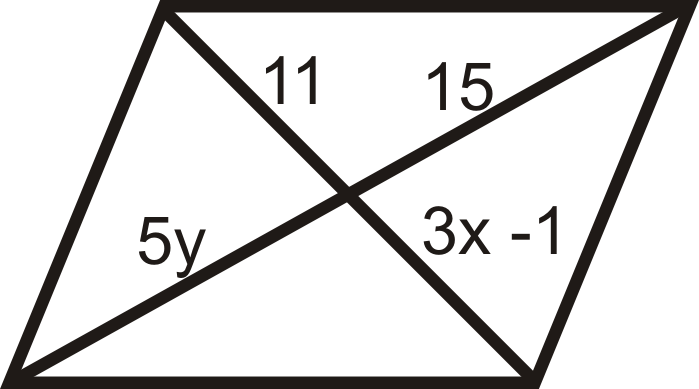
Малюнок\(\PageIndex{31}\)

З питань 19-22 визначте, чи\(ABCD\) є паралелограм.

\(A(8,−1)\),\(B(6,5)\),\(C(−7,2)\),\(D(−5,−4)\)
\(A(−5,8)\),\(B(−2,9)\),\(C(3,4)\),\(D(0,3)\)
\(A(−2,6)\),\(B(4,−4)\),\(C(13,−7)\),\(D(4,−10)\)
\(A(−9,−1)\),\(B(−7,5)\),\(C(3,8)\),\(D(1,2)\)

Заповніть пропуски в докази нижче.

Теорема протилежних кутів

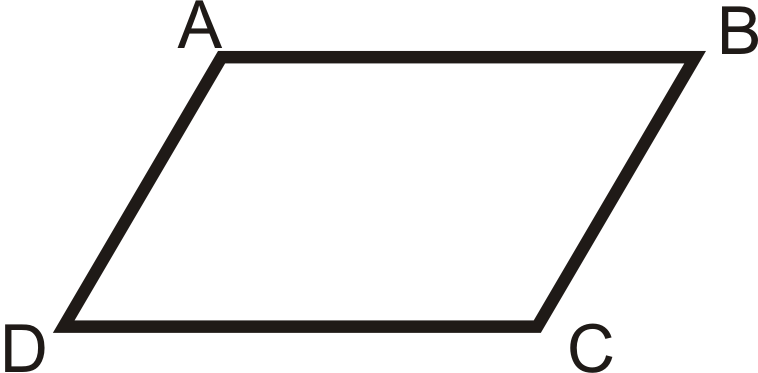
F-д_14С5С7АФ 431574174Ф61Е564Б4С1С17А9Ф6Ф Ф 030Е565Б85454С6+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{32}\)

З огляду на:\(\angle A\cong \angle C\),\(\angle D\cong \angle B\)

Доведіть:\(ABCD\) це паралелограм

*Заява*	*Причина*
1.	1.
2. \(m\angle A=m\angle C\),\(m\angle D=m\angle B\)	2.
3.	3. Визначення чотирикутника
4. \(m\angle A+m\angle A+m\angle B+m\angle B=360^{\circ}\)	4.
5.	5. Поєднуйте як терміни
6.	6. Відділ\(PoE\)
7. \(\angle A\)і\(\angle B\) є додатковими\(\angle A\) і\(\angle D\) є додатковими	7.
8.	8. Послідовні внутрішні кути Converse
9. \(ABCD\)є паралелограмом	9.

Теорема діагоналей паралелограма

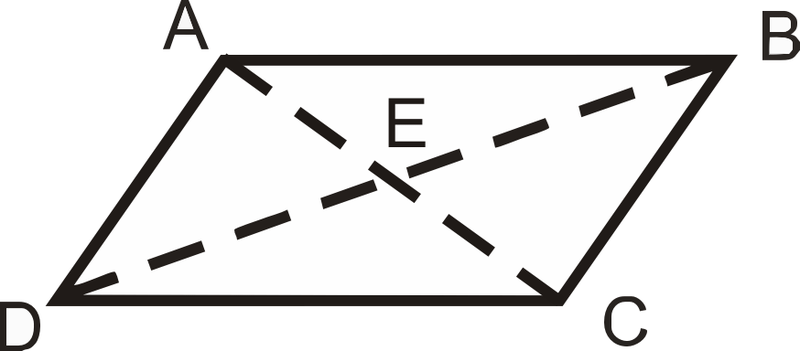
F-д_4С50CDD807989540195FFB2226DF7DC09513FF33267308D9F8F8203CA8+зображення_крихіткий+зображення_крихіткий_png — Малюнок\(\PageIndex{33}\)

З огляду на:\(\overline{AE}\cong \overline{EC}\),\(\overline{DE}\cong \overline{EB}\)

Доведіть:\(ABCD\) це паралелограм

*Заява*	*Причина*
1.	1.
2.	2. Теорема про вертикальні кути
3. \(\Delta AED \cong \Delta CEB\) \(\Delta AEB\cong \Delta CED\)	3.
4.	4.
5. \(ABCD\)є паралелограмом	5.

З огляду на:\(\angle ADB\cong \angle CBD\),\(\overline{AD}\cong \overline{BC}\)

Доведіть:\(ABCD\) це паралелограм

*Заява*	*Причина*
1.	1.
2. \(\overline{AD}\parallel\overline{BC}\)	2.
3. \(ABCD\)є паралелограмом	3.

Огляд (Відповіді)

Щоб переглянути відповіді на рецензію, відкрийте цей PDF-файл і знайдіть розділ 6.4.

Додаткові ресурси

Інтерактивний елемент

Відео: Доведення чотирикутника - це принципи паралелограма - Основні

Діяльність: Чотирикутники, які є паралелограмами Питання обговорення

Навчальні посібники: паралелограми навчальний посібник

Практика: Докази паралелограма

Реальний світ: чотирикутники, які є паралелограмами