2.17: Докази за участю трикутників
- Page ID
- 54548
Довести теореми про суму кутів, базових кутів рівнобедрених трикутників та зовнішніх і внутрішніх кутів.
Теореми про трикутники
Нагадаємо, що трикутник - це форма з рівно трьома сторонами. Трикутники можна класифікувати за їх сторонами та кутами.
Класифікуючи трикутник за його сторонами, ви повинні подивитися, чи є будь-яка зі сторін однакової довжини.
- Якщо жодні сторони не мають однакової довжини, то це сходовий трикутник.
- Якщо дві сторони однакової довжини, то це рівнобедрений трикутник.
- Якщо всі три сторони мають однакову довжину, то це рівносторонній трикутник.

При класифікації трикутника за його кутами слід дивитися на розміри кутів:
- Якщо трикутник має прямий кут, то це прямокутний трикутник.
- Якщо міри всіх кутів в трикутнику менше\(90^{\circ}\), то це гострий трикутник.
- Особливий випадок гострого трикутника - це коли всі три кути рівні. У такому випадку всі три кути становлять 60 градусів, і вони утворюють рівнокутний трикутник.
- Якщо міра одного кута в трикутнику більше\(90^{\circ}\), то це тупий трикутник.

Теорема про суму трикутника
Доведіть, що внутрішні кути трикутника сума до\(180^{\circ}\).
Це властивість трикутників, про які ви чули і використовували раніше, але ви, можливо, ніколи не бачили доказів того, чому це правда. Ось доказ формату абзацу, який спирається на паралельні лінії та альтернативні внутрішні кути.
Розглянемо загальний трикутник нижче.
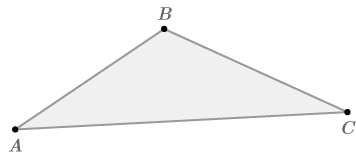
За паралельним постулатом існує рівно одна лінія, паралельна\ overline {AC}\) через B\). Намалюйте цю лінію.

\( \angle DBA\cong \angle A because they are alternate interior angles and alternate interior angles are congruent when lines are parallel. Therefore, \(m\angle DBA=m\angle A\). Аналогічно,\(\angle EBC\cong \angle C\) тому що вони також чергують внутрішні кути, і так\(m\angle EBC=m\angle \). \(m\angle DBA+m\angle ABC+m\angle EBC=180^{\circ}\)тому що ці три кути утворюють пряму лінію. Шляхом підміни,\(m\angle A+m\angle ABC+m\angle C=180^{\circ}\).

Твердження "сума мір внутрішніх кутів трикутника є\(180^{\circ}\)" відоме як Теорема про суму трикутника. Тепер, коли це було доведено, ви можете використовувати його в майбутніх доказах, не доводячи це знову.
Клацніть маленьку синю стрілку поруч із зображенням нижче, а потім перетягніть помаранчеві вершини, щоб змінити форму трикутника. Зверніть увагу, що сума мір внутрішніх кутів трикутника завжди\(180^{\circ}\).

Теорема про рівнобедрене трикутник
Довести, що базові кути рівнобедреного трикутника є конгруентними.
Базовими кутами рівнобедреного трикутника є кути, протилежні конгруентним сторонам. Нижче розмічаються базові кути для рівнобедрених\(\Delta ABC\).

Ви повинні довести, що\(\angle B\cong \angle C\) враховуючи це\(\overline{AB}\cong \overline{AC}\). Ось доказ у форматі двох стовпців, який спирається на бісектриси кута та конгруентні трикутники. Доказ буде посилатися на малюнок нижче.

|
Заяви |
причини |
|
Рівнобедрений\(\Delta ABC\) |
Враховується |
| \(\overline{AB}\cong \overline{AC}\) |
Визначення рівнобедреного трикутника |
|
Побудувати\(\overrightleftarrow{AD}\), кут бісектриси\(\angle A\), з\(F\) перетином\(\overline{BC}\) і\(\overrightleftarrow{AD}\) |
Кут має лише одну бісектрису кута |
| \(\overline{AF}\cong \overline{AF}\) |
Рефлексивне властивість |
| \(\angle BAF\cong \angle CAF\) |
Визначення бісектриси кута |
|
\(\Delta ABF\cong \Delta ACF\) |
\(SAS\cong\) |
| \(\angle B\cong \angle C\) |
\(CPCTC\) |
Твердження "базові кути рівнобедреного трикутника конгруентні" є теоремою про рівнобедрений трикутник. Тепер, коли це було доведено, ви можете використовувати його в майбутніх доказах, не доводячи це знову.
Клацніть маленьку синю стрілку поруч із зображенням нижче, а потім перетягніть помаранчеві вершини, щоб змінити форму трикутника. Зверніть увагу, що базові кути рівнобедреного трикутника завжди конгруентні.

Інтерактивний елемент
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Теорема про зовнішні кути
Довести, що міра зовнішнього кута трикутника дорівнює сумі мір віддалених внутрішніх кутів.
Зовнішній кут трикутника - це кут поза трикутником, створений шляхом розширення однієї зі сторін трикутників. Внизу\(\angle ACD\) - зовнішній кут. Для зовнішнього кута\(\angle ACD\) кути\(\angle A\) і\(\angle B\) є віддаленими внутрішніми кутами, тому що вони є внутрішніми кутами, які не примикають до зовнішнього кута.

Ось схема потоку доказ цієї теореми.
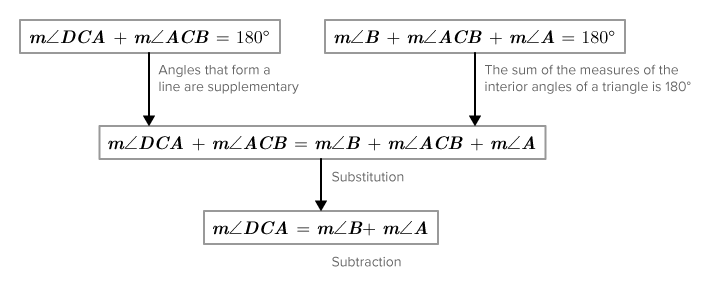
Твердження «міра зовнішнього кута трикутника дорівнює сумі мір віддалених внутрішніх кутів» є теоремою зовнішніх кутів. Тепер, коли це було доведено, ви можете використовувати його в майбутніх доказах, не доводячи це знову.
Клацніть маленьку синю стрілку поруч із зображенням нижче, а потім перетягніть помаранчеві вершини, щоб змінити форму трикутника. Виберіть два віддалених внутрішніх кута трикутника і спостерігайте, як міра зовнішнього кута залишається рівною сумі віддалених внутрішніх кутів.

В інтерактивному нижче перемістіть червоні точки, щоб змінити форму трикутника. Перемістіть сині точки, щоб порівняти кути\ кут 1\),\ кут 2\) і\ кут 3\).
Зверніть увагу, що оскільки вони вертикальні кути, кутові пари\(m\angle 1=m\angle 4\)\(m\angle 2=m\angle 5\), і\(m\angle 3=m\angle 6\).
Інтерактивний елемент
Додайте тут інтерактивний текст елемента. Це поле НЕ буде друкувати в PDF-файлах
Теорема середнього сегмента трикутника
У трикутнику нижче точка D - середина,\(\overline{AC}\)\(E\) а точка - середина\(\overline{BC}\). Зробіть здогадки про те, як\(\overline{DE}\) ставиться до\(\overline{AB}\).

Гіпотеза - це здогадка про те, що може бути правдою. Зробивши здогадки, зазвичай ви будете намагатися це довести. Дві можливі припущення:
- \(\overline{DE} \parallel \overline{AB}\)
- Довжина\(\overline{DE}\) дорівнює половині довжини\(\overline{AB}\)
Розглянемо малюнок нижче.

Щоб довести гіпотезу\ (DE\ паралельно AB, нам потрібно довести, що\ (\ Delta FEB\ cong\ Delta DEC, яку ми потім використовуємо, щоб довести, що\ (BF\ паралельний змінний струм. Потім ми продовжуємо з доказом довести, що\ (\ Delta ADB\ cong\ Delta FBD який потім призводить нас довести, що\ (DE\ паралельно AB.
|
Заяви |
причини |
|
|
1. |
\(\overline{DC}\cong \overline{AD}\),\(\overline{CE}\cong \overline{EB}\),\(\overline{DE}\cong \overline{EF}\) |
Враховується |
| \(\angle CED\cong \angle FEB\) |
Вертикальні кути конгруентні |
|
| \(\Delta FEB\cong \Delta DEC\) | \(SAS\cong\) | |
|
2. |
\(\angle FBE\cong \angle ECD\) |
\(CPCTC\) |
| \(\overline{BF} \parallel \overline{AC}\) |
Якщо альтернативні внутрішні кути конгруентні, то лінії паралельні. |
|
|
3. |
\(\angle ADB\cong \angle DBF\) |
Якщо лінії паралельні, то альтернативні внутрішні кути конгруентні. |
| \(\overline{DB}\cong \overline{DB}\) |
Рефлексивне властивість |
|
| \(\overline{BF}\cong \overline{DC}\) |
\(CPCTC\) |
|
| \(\overline{BF}\cong \overline{AD}\) |
Заміна |
|
| \(\Delta ADB\cong \Delta FBD\) | \(SAS\cong\) | |
|
4. |
\(\angle ABD\cong \angle FDB\) |
\(CPCTC\) |
| \(\overline{DE} \parallel \overline{AB}\) |
Якщо альтернативні внутрішні кути конгруентні, то лінії паралельні. |
Ось цифра знову, для довідки:

Тепер доведіть здогадки про те, що довжина\(DE is half the length of \(AB\).
| Заяви | причини | |
| 5. | \(\overline{DF}\parallel \overline{AB}\) | \(\overline{DE}\)виробляється в\(F\) |
| \(\overline{BF}\parallel \overline{AD}\) | \(D\)є середньою точкою\(AC\) | |
| \(ABFD\)є паралелограмом | Визначення паралелограма | |
| \(\overline{DE}=\dfrac{1}{2} \overline{DF}\) | \(\overline{DE}\cong \overline{EF}\) | |
| \(\overline{DE}=\dfrac{1}{2} \overline{AB}\) | Визначення паралелограма |
Таким чином, відрізок лінії, що з'єднує середні точки будь-яких двох сторін трикутників, паралельний третій стороні і дорівнює половині її, це теорема трикутника середнього сегмента. Зверніть увагу, що існують інші способи довести, що два сегменти паралельні. Один метод спирається на подібні трикутники, які будуть вивчені в іншій концепції.
Натисніть на маленьку синю стрілку поруч із зображенням нижче, а потім перетягніть помаранчеві вершини, щоб змінити форму трикутника. Зверніть увагу, що відрізок лінії, що з'єднує середні точки двох сторін трикутника, паралельний третій стороні і дорівнює половині її.

CK-12 PLIX Інтерактивний
Інтерактивний елемент
Рецензія
1. Раніше ви довели, що сума внутрішніх кутів трикутника\(180^{\circ}\) (теорема про суму трикутника), використовуючи доказ абзацу. Тепер перепишіть цей доказ у форматі двох стовпців.
2. Знову перепишіть доказ теореми про суму трикутника, цього разу у форматі блок-схеми.
3. Раніше ви довели, що базові кути рівнобедреного трикутника конгруентні за допомогою двоколонкового доказу. Тепер перепишіть цей доказ у форматі абзацу.
4. Знову перепишіть теорему про трикутник, на цей раз у форматі блок-схеми.
5. Раніше ви довели, що міра зовнішнього кута трикутника дорівнює сумі мір віддалених внутрішніх кутів за допомогою формату блок-діаграми. Тепер перепишіть цей доказ у форматі абзацу.
6. Знову перепишіть зовнішні кути доказ, на цей раз у форматі двох стовпців.
7. Нагадаємо, що відрізок, що з'єднує середні точки двох сторін трикутника, паралельний третій стороні трикутника. З огляду на наведену нижче діаграму і що,\(\Delta ADB\cong \Delta FBD\) як доведено раніше на уроці, доведіть це\(DE=\dfrac{1}{2} AB\).
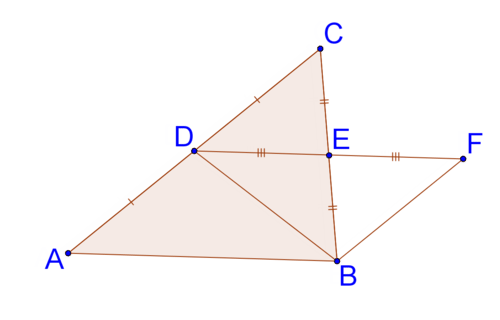
8. Що таке зворотне: «якщо трикутник рівнобедрений, базові кути конгруентні?» Чому ви вважаєте, що зворотне також вірно чи не відповідає дійсності?
9. Доведіть, що якщо два кути трикутника є конгруентними, то трикутник рівнобедрений. Скористайтеся діаграмою та двоколонковим доказом нижче та заповніть пробіли, щоб завершити доказ.
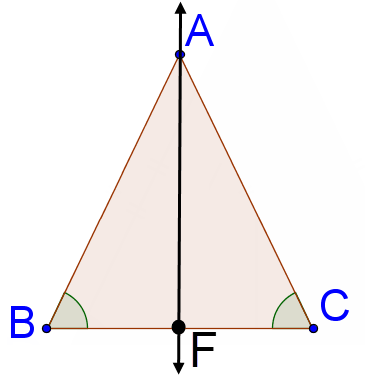
|
Заяви |
причини |
| \(\angle B\cong \angle C\) |
________ |
|
Побудувати\(\overrightleftarrow{AF}\), кут бісектриси\(\angle A\), з\(F\) перетином\(\overline{BC}\) і\(\overrightleftarrow{AF}\) |
Кут має лише одну бісектрису кута |
| ________ |
Визначення бісектриси кута |
|
________ |
Рефлексивне властивість |
| \(\Delta ABF\cong \Delta ACF\) | ________ |
| ________ |
\(CPCTC\) |
10. Перепишіть доказ того, що трикутник з двома конгруентними кутами є рівнобедреним у форматі блок-схеми.
11. Перепишіть рівнобедрений трикутник доказ у форматі абзацу.
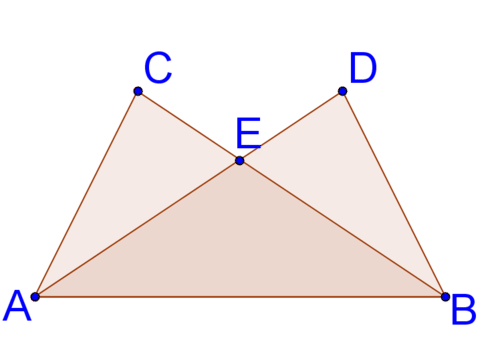
12. Враховуючи\(\Delta ABC\cong \Delta BAD\), що, довести,\(\Delta AEB\) що рівнобедрений.
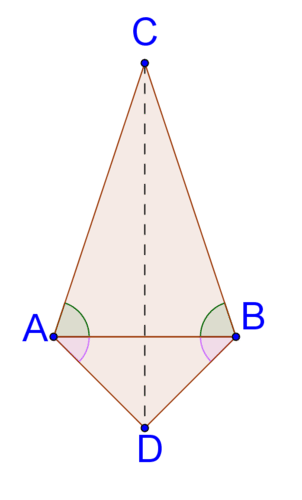
13. З огляду на маркування на малюнку нижче, поясніть,\(\overline{CD}\) чому перпендикулярна бісектриса\(\overline{AB}\).
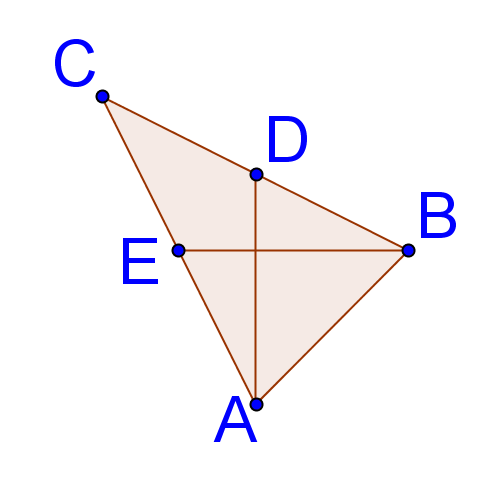
14. На малюнку нижче,\(\Delta ABC is isosceles with \(\overline{AC}\cong \overline{CB}\). \(E\)є середньою точкою\(\overline{AC}\) і\(D\) є серединою\(\overline{CB}\). Доведіть, що\(\Delta EAB\cong \Delta DBA\).
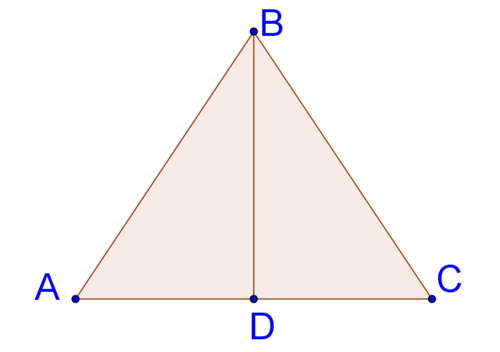
15. Поясніть, чому знання того, що\(\DeltaABC\) є рівнобедреним, недостатньо інформації, щоб довести це\(\DeltaABD\cong \DeltaCBD\).
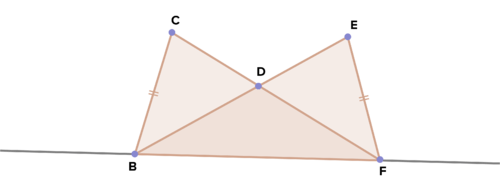
16 дано:\(\angle CBD\cong \angle EFD\);\(\overline{CB}\cong \overline{EF}\)
Доведіть:\(\angle DBF\cong \angle DFB\)

17. Дано:\(\overline{BC}\cong \overline{EF}\);\(\overline{CF}\cong \overline{EB}\)
Доведіть:\(\Delta BDF\) рівнобедрений
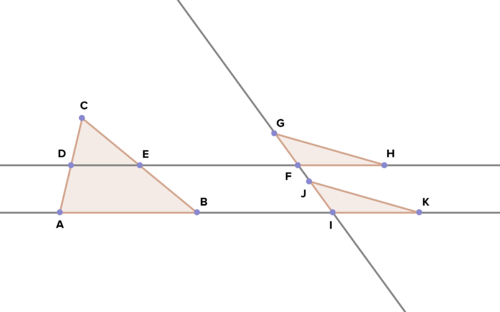
18. Дано:\(\overline{DE}\) середній сегмент\(\Delta ABC \)\(\overline{GF}\cong \overline{JI}\);\(\overline{FH}\cong \overline{IK}\)
Доведіть:\(\Delta GFH \cong \Delta JIK\)
Огляд (Відповіді)
Щоб переглянути відповіді на огляд, натисніть тут.
Додаткові ресурси
Інтерактивний елемент
Практика: Докази за участю трикутників