Skip to main content
LibreTexts - Ukrayinska

2.7: Дедуктивні міркування

  1. Last updated
  2. Save as PDF
  • Page ID
    54526

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Робимо висновки з фактів.

    Дедуктивне міркування тягне за собою висновок з фактів. При використанні дедуктивних міркувань є кілька законів, які корисно знати.

    Закон відстороненості: Якщо\(p\rightarrow q\) правда, і\(p\) правда, то\(q\) це правда. Дивіться приклад нижче.

    Ось два правдивих твердження:

    1. Якщо число непарне (p), то це сума парного і непарного числа (q).
    2. 5 - непарне число (конкретний приклад p).

    Висновок повинен бути, що 5 - це сума парного і непарного числа (q).

    Закон контрапозитиву: Якщо\(p\rightarrow q\) це правда і\(\sim q\) правда, то ви можете зробити висновок\(\sim p\). Дивіться приклад нижче.

    Ось два правдивих твердження:

    1. Якщо студент знаходиться в Geometry (\(p\)), то він або вона здала алгебру I (\(q\)).
    2. Данило не пройшов Алгебру I (конкретний приклад\(\sim q\) ).

    Висновок повинен бути, що Даніель не в Geometry (\(\sim q\)) .

    Закон силогізму: Якщо\(p\rightarrow q\) і\(q\rightarrow r\) є істинними, то\(p\rightarrow r\) це правда. Дивіться приклад нижче.

    Ось три правдивих твердження:

    1. Якщо Піт запізнився (\(p\)), Марк запізниться (\(q\)).
    2. Якщо Марк запізнився (\(q\)), Карл запізниться (\(r\)).
    3. Піт запізнився (\(p\)).

    Зверніть увагу, як кожне «потім» стає наступним «if» у ланцюжку тверджень. Якщо Піт запізнився, це починає ефект доміно запізнення. Марк запізниться, а Карл теж запізниться. Отже, якщо Піт спізнюється, то Карл запізниться (\(r\)), є логічним завершенням.

    Що робити, якщо вам дали факт на кшталт «Якщо ви запізнилися на заняття, ви отримаєте затримання»? Які висновки ви могли б зробити з цього факту?

    Приклад\(\PageIndex{1}\)

    Припустимо, Беа робить такі твердження, які, як відомо, вірні.

    Якщо Центральна середня школа сьогодні переможе, вони підуть на регіональний турнір. Центральна середня школа сьогодні перемогла.

    Який логічний висновок?

    Рішення

    Це справжні твердження, які ми можемо сприймати як факти. Висновок такий: Центральна гімназія піде на регіональний турнір.

    Приклад\(\PageIndex{2}\)

    Ось два правдивих твердження.

    Якщо\(\angle A\) і\(\angle B\) є лінійною парою, то\(m\angle A+m\angle B=180^{\circ}\).

    \(\angle ABC\)і\(\angle CBD\) являють собою лінійну пару.

    Який висновок можна зробити з цього?

    Рішення

    Це приклад Закону відстороненості, тому:

    \(m\angle ABC+m\angle CBD=180^{\circ}\)

    Приклад\(\PageIndex{3}\)

    Визначте висновок з істинних тверджень нижче.

    Немовлята носять підгузники.

    Мій маленький брат не носить памперси.

    Рішення

    Друге твердження є еквівалентом\(\sim q\). Тому висновок такий\(\sim p\), або: Мій маленький брат не дитина.

    Приклад\(\PageIndex{4}\)

    Ось два правдивих твердження.

    Якщо\(\angle A\) і\(\angle B\) є лінійною парою, то\(m\angle A+m\angle B=180^{\circ}\).

    \(m\angle 1=90^{\circ}\)і\(m\angle 2=90^{\circ}\).

    Який висновок можна зробити з цих двох тверджень?

    Рішення

    Тут немає висновку. Ці заяви мають форму:

    \(p \rightarrow q\)

    \(q\)

    Ми не можемо зробити висновок, що\(\angle 1\) і\(\angle 2\) є лінійною парою.

    Ось два контрприклади:

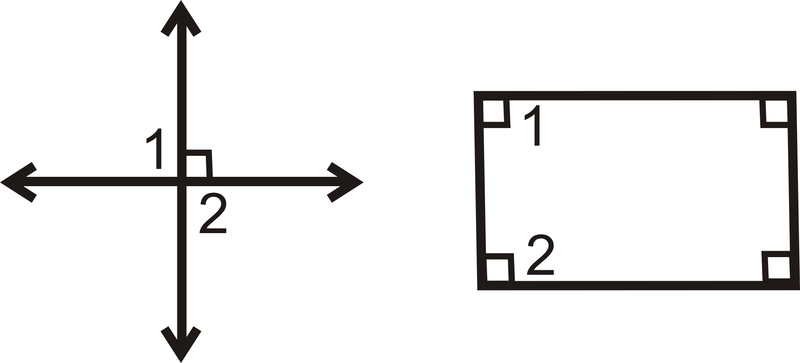    F-д_3730Ф4А 4430237E289E1E3844D9E623F903ЕЕФ 3ФДК034Б34А8FF99+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{1}\)

    Приклад\(\PageIndex{5}\)

    Визначте висновок з істинних тверджень нижче.

    Якщо ви не в Чикаго, то ви не можете бути на\(L\).

    Саллі знаходиться на\(L\).

    Рішення

    Якби ми переписали це символічно, це виглядало б так:

    \(\sim p \rightarrow \sim q\)

    \(q\)

    Незважаючи на те, що це виглядає трохи інакше, це приклад Закону про контрапозитив. Тому логічний висновок такий: Саллі знаходиться в Чикаго.

    Рецензія

    Визначте логічний висновок і встановіть, який закон ви використовували (Закон відстороненості, Закон контрапозитиву, або Закон силогізму). Якщо ніякого висновку зробити не вдається, напишіть «немає висновку».

    1. Люди, які голосують за Джейн Wannabe, розумні люди. Я проголосувала за Джейн Ваннаб.
    2. Якщо Rae є водієм сьогодні, то Марія - водій завтра. Енн сьогодні водій.
    3. Всі рівнокутні трикутники рівносторонні. \(\delta ABC\)рівнокутна.
    4. Якщо переможе Північ, то виграє Захід. Якщо Захід виграє, то Схід програє.
    5. Якщо\(z>5\), то\(x>3\). Якщо\(x>3\), то\(y>7\).
    6. Якщо мені холодно, то ношу куртку. Я не ношу куртку.
    7. Якщо на вулиці йде дощ, то мені потрібен парасольку. На вулиці не йде дощ.
    8. Якщо фігура - це коло, то вона ніколи не закінчується. Якщо вона ніколи не закінчується, то вона ніколи не починається. Якщо він ніколи не запускається, то його не існує. Якщо його немає, то нам не потрібно його вивчати.
    9. Якщо ви надсилаєте текст під час руху, значить, ви небезпечні. Ви безпечний водій.
    10. Якщо ви носите сонцезахисні окуляри, то на вулиці сонячно. Ви носите сонцезахисні окуляри.
    11. Якщо ви носите сонцезахисні окуляри, то на вулиці сонячно. Хмарно.
    12. Я приберу свою кімнату, якщо мама попросить мене. Я не прибираю свою кімнату.
    13. Напишіть символічне зображення #8. Включіть свій висновок. Чи має цей аргумент сенс?
    14. Напишіть символічне зображення #10. Включіть свій висновок.
    15. Напишіть символічне зображення #11. Включіть свій висновок.

    Ресурси

    Лексика

    Термін Визначення
    Дедуктивні міркування Використовуючи дедуктивні міркування, можна було б зробити висновки, які ґрунтуються на фактах.

    Додаткові ресурси

    Відео: Види міркувань: дедуктивні принципи - основні

    Види діяльності: Дедуктивні міркування Дискусійні питання

    Навчальні посібники: типи міркувань навчальний посібник

    Практика: Дедуктивні міркування

    Реальний світ: дедуктивні міркування