Skip to main content
LibreTexts - Ukrayinska

2.13: Вступ до доказів

  1. Last updated
  2. Save as PDF
  • Page ID
    54532

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Використовуйте два стовпці доказів, щоб стверджувати і довести обґрунтованість твердження шляхом написання формальних аргументів математичних тверджень. Також дізнайтеся про формати доказів абзаців та блок-діаграм.

    Дві колонки Докази

    Двоколонковий доказ - це один із поширених способів організації доказу в геометрії. Двоколонкові докази завжди мають два стовпці: один для тверджень і один з причин. Найкращий спосіб зрозуміти докази з двома стовпцями - прочитати приклади.

    При написанні власного доказу з двох стовпців майте на увазі такі речі:

    • Пронумеруйте кожен крок.
    • Почніть з наданої інформації.
    • Висловлювання з тією ж причиною можна об'єднати в один крок. Це вирішувати вам.
    • Намалюйте картинку і позначте її заданою інформацією.
    • У вас повинна бути причина для КОЖНОГО твердження.
    • Порядок тверджень у доказі не завжди фіксується, але переконайтеся, що порядок має логічний сенс.
    • Причинами будуть визначення, постулати, властивості і раніше доведені теореми. «Giden» використовується лише як причина, якщо інформація у стовпці оператора була надана в задачі.
    • Використовуйте символи та абревіатури для слів у доказах. Наприклад,\(\cong\) може використовуватися замість слова конгруентний. Ви також можете використовувати\ (\ кут) для слова кут.

    Припустимо, вам кажуть, що\(\angle XYZ\) це прямий кут і що\(\overrightarrow{YW}\) бісекції\(\angle XYZ\). Потім вас просять довести\(\angle XYW\cong \angle WYZ\).

    Приклад\(\PageIndex{1}\)

    Напишіть докази з двох стовпців для наступного:

    Якщо\(A\),\(B\),\(C\), і\(D\) є точками на прямій, в заданому порядку, і\(AB=CD\), то\(AC=BD\).

    Рішення

    Коли твердження дається таким чином, частина «якщо» - це дана, а частина «тоді» - це те, що ми намагаємося довести.

    Завжди починайте з малювання картини того, що вам дано.

    Покладіть точки в порядку\(A\),\(B\),\(C\),,\(D\) на лінії.

    Ф-Д_С0Б0КФ 92С9ФЕ28800 БА 8Б 560ДА359 АЦ06С 5Ф4С4 БК9ДБ8А9Е3ЕФЕ2+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    Додайте дане,\(AB=CD\).

    Ф-д_С2А 1806254611 АФ 4120698 ФД8Б46А4ФД 2С557336 ААД 9C8F58C0AB+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{2}\)

    Намалюйте докази з двох стовпців і почніть з заданої інформації.

    Заява Причина
    1. \(A\),\(B\),\(C\), і\(D\) є колінеарними, в такому порядку. 1. Враховується
    2. \(AB=CD\) 2. Враховується
    3. \(BC=BC\) 3. Рефлексивний PoE
    4. \(AB+BC=BC+CD\) 4. Додаток PoE

    5. \(AB+BC=AC\)

    \(BC+CD=BD\)

    		 5. Постулат додавання сегмента
    6. \(AC=BD\) 6. Заміна або перехідний PoE

    Приклад\(\PageIndex{2}\)

    Напишіть докази з двох стовпців.

    Дано:\(\overrightarrow{BF}\) бісекти\(\angle ABC\);\(\angle ABD\cong \angle CBE\)

    Доведіть:\(\angle DBF\cong \angle EBF\)

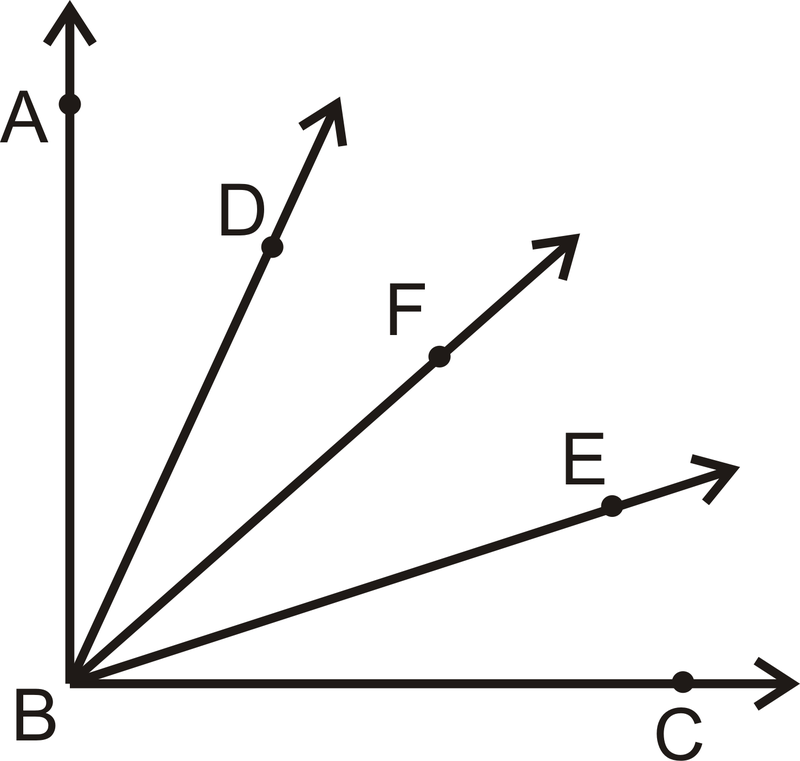    F-D_3F8 ДБ750Б593C DEF 4Е 8667ФД82405Д4Б3СБ 482А07Б311DE5B378A30+зображення_крихіткий+зображення_крихіткий.PNGМалюнок\(\PageIndex{3}\)

    Рішення

    Спочатку нанесіть відповідну розмітку на малюнку. Нагадаємо, що бісекція означає «розрізати навпіл». Тому,\(m\angle ABF=m\angle FBC\).


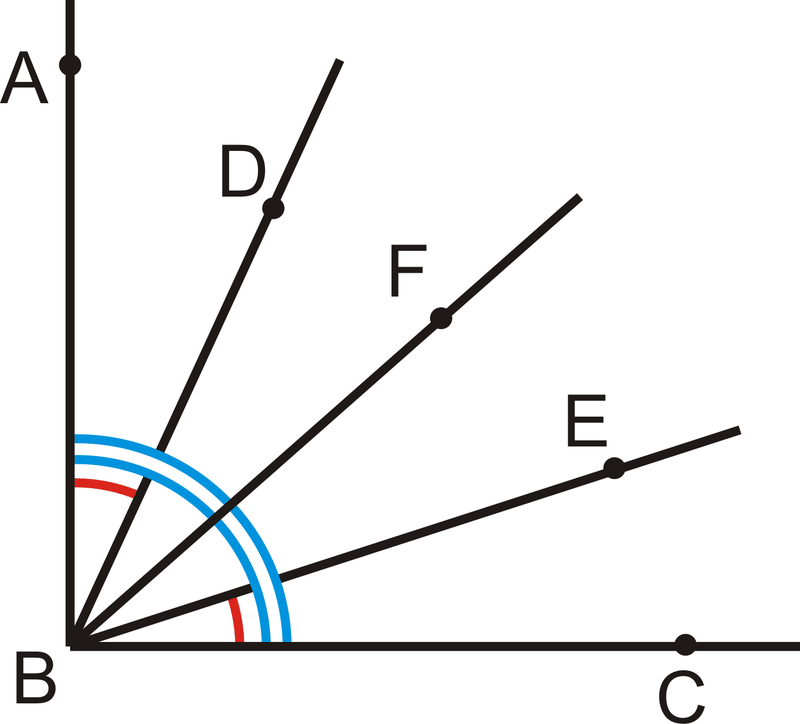
    F-д_С53АФ55Д7А322745826D215207C8222716692E1А0Б9ФЦ10Ф65Б718+зображення_крихіткий+зображення_крихіткий_крошечкий.PNG
    Малюнок\(\PageIndex{4}\)
    Заява Причина
    1. \(\overrightarrow{BF}\)бісекції\(\angle ABC\),\(\angle ABD\cong \angle CBE\) 1. Враховується
    2. \(m\angle ABF=m\angle FBC\) 2. Визначення бісектриси кута
    3. \(m\angle ABD=m\angle CBE\) 3. Якщо кути є\(\cong\), то їх мірки рівні.

    4. \(m\angle ABF=m\angle ABD+m\angle DBF\)

    \(m\angle FBC=m\angle EBF+m\angle CBE\)

    		 4. Постулат додавання кута
    5. \(m\angle ABD+m\angle DBF=m\angle EBF+m\angle CBE\) 5. Підміна PoE
    6. \(m\angle ABD+m\angle DBF=m\angle EBF+m\angle ABD\) 6. Підміна PoE
    7. \(m\angle DBF=m\angle EBF\) 7. Віднімання PoE
    8. \(\angle DBF\cong \angle EBF\) 8. Якщо міри рівні, то кути дорівнюють\ (\ cong.

    Приклад\(\PageIndex{3}\)

    Теорема прямого кута стверджує, що якщо два кути є прямими кутами, то кути є конгруентними. Доведіть цю теорему.

    Щоб довести цю теорему, створіть власний малюнок і назвіть деякі кути так, щоб у вас були конкретні кути, про які можна говорити.

    Дано:\(\angle A\) і\(\angle B\) є прямими кутами

    Доведіть:\(\angle A\cong \angle B\)

    Рішення

    Заява Причина
    1. \(\angle A\)і\(\angle B\) є прямими кутами 1. Враховується
    2. \(m\angle A=90^{\circ}\)і\(m\angle B=90^{\circ}\) 2. Визначення прямих кутів
    3. \(m\angle A=m\angle B\) 3. Перехідний PoE
    4. \(\angle A\cong \angle B\) 4. \(\cong\)кути мають = заходи

    Будь-який раз, коли прямі кути згадуються в доказі, вам потрібно буде використовувати цю теорему, щоб сказати, що кути є конгруентними.

    Приклад\(\PageIndex{4}\)

    Теорема про однакові кутові добавки стверджує, що якщо два кути є додатковими до одного кута, то два кути є конгруентними. Доведіть цю теорему.

    Задано:\(\angle A\) і\(\)\ кут B є додатковими кутами. \(\angle B\)і\(\angle C\) є додатковими кутами.

    Доведіть:\(\angle A\cong \angle C\)

    Рішення

    Заява Причина

    1. \(\angle A\)і\(\angle B\) є додатковими

    \(\angle B\)і\(\angle C\) є додатковими

    		 1. Враховується

    2. \ (м\ кут A+м\ кут B = 180^ {\ circ}

    \ (м\ кут B+м\ кут C = 180^ {\ circ}

    		 2. Визначення додаткових кутів
    3. \(m\angle A+m\angle B=m\angle B+m\angle C\) 3. Підміна PoE
    4. \(m\angle A=m\angle C\) 4. Віднімання PoE
    5. \(\angle A\cong \angle C\) 5. \(\cong\)кути мають = заходи

    Приклад\(\PageIndex{5}\)

    Теорема вертикальних кутів стверджує, що вертикальні кути є конгруентними. Доведіть цю теорему.

    Задано: Лінії\(k\) і\(m\) перетинаються.

    Доведіть:\(\angle 1\cong \angle 3\)

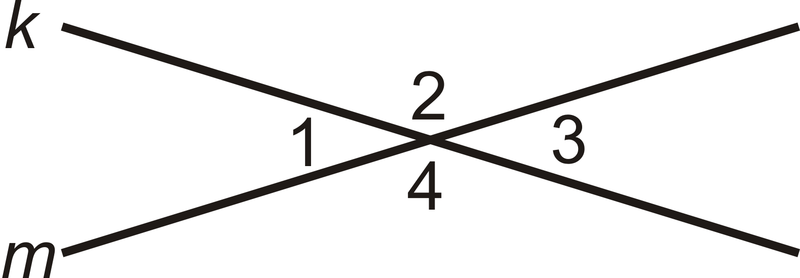
    F-D_A48601A6F3B2 САД 7454719А7БА 6Д7СБ2Е755Б3854Д83БАЕ8Ф3АА+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{5}\)

    Рішення

    Заява Причина
    1. Лінії\(k\) і\(m\) перетин 1. Враховується

    2. \(\angle 1\)і\(\angle 2\) є лінійною парою

    \(\)\ кут 2 і\(\angle 3\) є лінійною парою

    		 2. Визначення лінійної пари

    3. \(\angle 1\)і\(\angle 2\) є додатковими

    \(\angle 2\)і\(\angle 3\) є додатковими

    		 3. Постулат лінійної пари

    4. \(m\angle 1+m\angle 2=180^{\circ}\)

    \(m\angle 2+m\angle 3=180^{\circ}\)

    		 4. Визначення додаткових кутів
    5. \(m\angle 1+m\angle 2=m\angle 2+m\angle 3\) 5. Підміна PoE
    6. \(m\angle 1=m\angle 3\) 6. Віднімання PoE
    7. \(\angle 1\cong \angle 3\) 7. \(\cong\)кути мають = заходи

    Приклад\(\PageIndex{6}\)

    \(\angle 1\cong \angle 4\)і\(\angle C\) і\(\angle F\) знаходяться під прямим кутом.

    Які кути є конгруентними і чому?

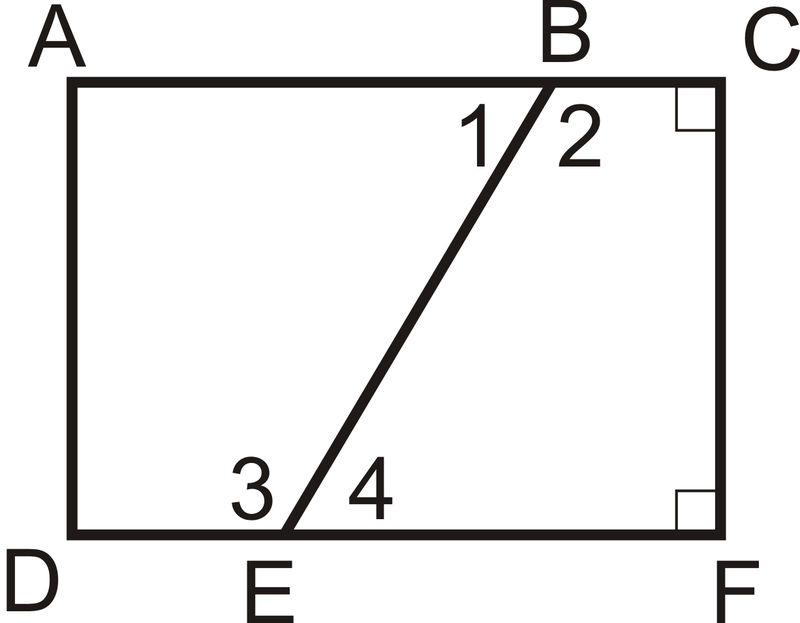
    Ф-Д_С1Е96Ф919536ДД8ДФ07Б0С96Ф91127C554C9АЦБ 470553431БД23D68+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{6}\)

    Рішення

    За теоремою прямого кута,\(\angle C\cong \angle F\). Крім того,\(\angle 2\cong \angle 3\) за тими ж кутами доповнює теорему тому, що\(\angle 1\cong \angle 4\) і вони є лінійними парами з цими конгруентними кутами.

    Рецензія

    Заповніть пропуски в докази нижче.

    1. Дано:\(\angle ABC\cong \angle DEF\) і\(\angle GHI\cong \angle JKL\)

    Доведіть:\(m\angle ABC+m\angle GHI=m\angle DEF+m\angle JKL\)

    Заява Причина
    1. 1. Враховується

    2. \(m\angle ABC=m\angle DEF\)

    \(m\angle GHI=m\angle JKL\)

    		 2.
    3. 3. Додаток PoE
    4. \(m\angle ABC+m\angle GHI=m\angle DEF+m\angle JKL\) 4.
    1. Дано:\(M\) є середньою точкою\(\overline{AN}\). \(N\)є середньою точкою\(\overline{MB}\)

    Доведіть:\(AM=NB\)

    Заява Причина
    1. Враховується
    2. Визначення середньої точки
    3. \(AM=NB\)
    1. Дано:\(\overline{AC}\perp \overline{BD}\) і\(\angle 1\cong \angle 4\)

    Доведіть:\(\angle 2\cong \angle 3\)

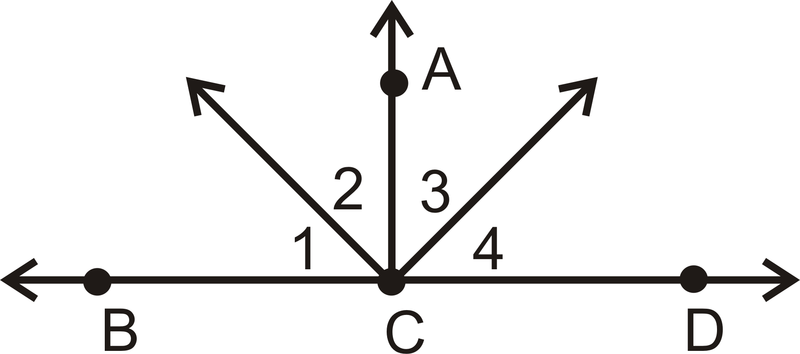
    F-д_36 ФАД5А56Е39Е8Е9Е0315Б90 А3311Е44 Е44 Е4Д 37Б1Ф4Е22ДФ1Д2728155+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{7}\)
    Заява Причина
    1. \ (\ overline {AC}\ perp\ overline {BD},\ (\ кут 1\ cong\ кут 4 1.
    2. \(m\angle 1=m\angle 4\) 2.
    3. 3. \ (\ Perp лінії створюють прямі кути

    4. \(m\angle ACB=90^{\circ}\)

    \(m\angle ACD=90^{\circ}\)

    		 4.

    5. \(m\angle 1+m\angle 2=m\angle ACB\)

    \(m\angle 3+m\angle 4=m\angle ACD\)

    		 5.
    6. 6. Заміна
    7. \(m\angle 1+m\angle 2=m\angle 3+m\angle 4\) 7.
    8. 8. Заміна
    9. 9. Віднімання PoE
    10. \(\angle 2\cong \angle 3\) 10.
    1. Дано:\(\angle MLN\cong \angle OLP\)

    Доведіть:\(\angle MLO\cong \angle NLP\)

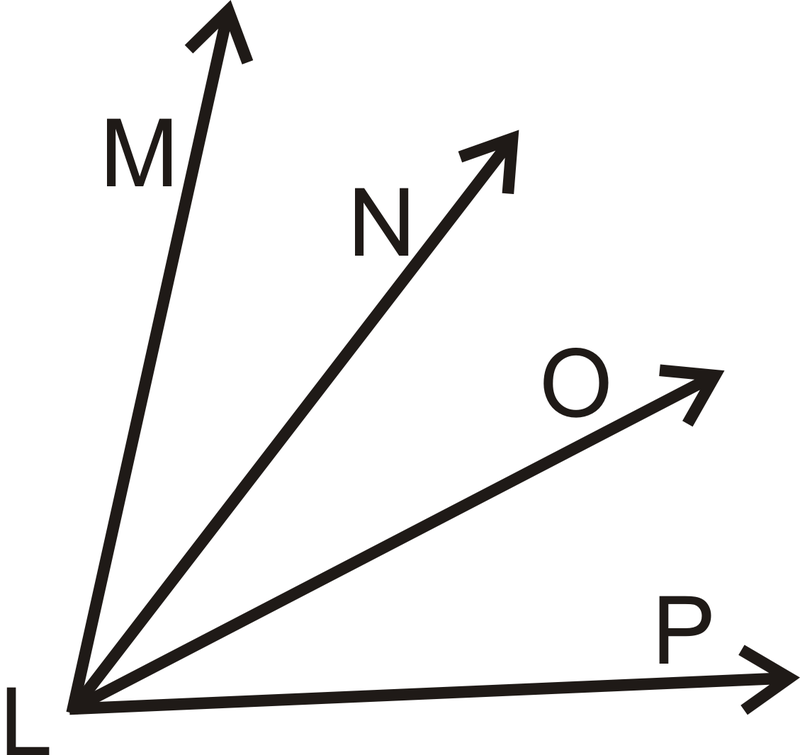
    F-D_A02B797 БББД бед 430c194906FCED 340А5БД4А3А321Ф1AE91872B280+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{8}\)
    Заява Причина
    1. 1.
    2. 2. \(\cong\)кути мають = заходи
    3. 3. Постулат додавання кута
    4. 4. Заміна
    5. \(m\angle MLO=m\angle NLP\) 5.
    6. 6. \(\cong\)кути мають = заходи
    1. Дано:\(\underline{AE}\perp \underline{EC}\) і\(\underline{BE}\perp \underline{ED}\)

    Доведіть:\(\angle 1\cong \angle 3\)

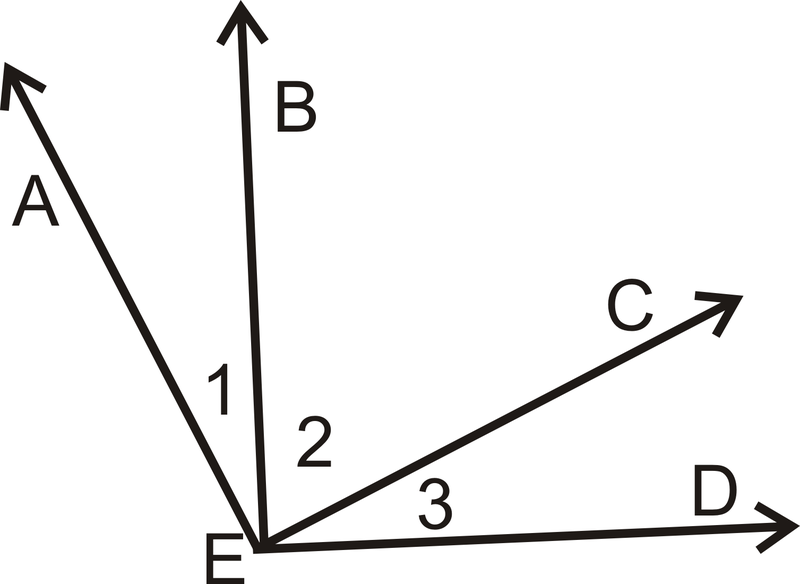
    Ф-Д_94Ф217649976Ф4А8Ф1078Д9ББ Б 76CFF39A1D4A118A506A28DF71050+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{9}\)
    Заява Причина
    1. 1.
    2. 2. \(\perp\)лінії створюють прямі кути

    3. \(m\angle BED=90^{\circ}\)

    \(m\angle AEC=90^{\circ}\)

    		 3.
    4. 4. Постулат додавання кута
    5. 5. Заміна
    6. \(m\angle 2+m\angle 3=m\angle 1+m\angle 3\) 6.
    7. 7. Віднімання PoE
    8. 8. \(\cong\)кути мають = заходи
    1. \(\angle L\)Враховується: є додатковим до\(\angle M\) і\(\angle P\) є додатковим до\(\angle O\) і\(\angle L\cong \angle O\)

    Доведіть:\(\angle P\cong \angle M\)

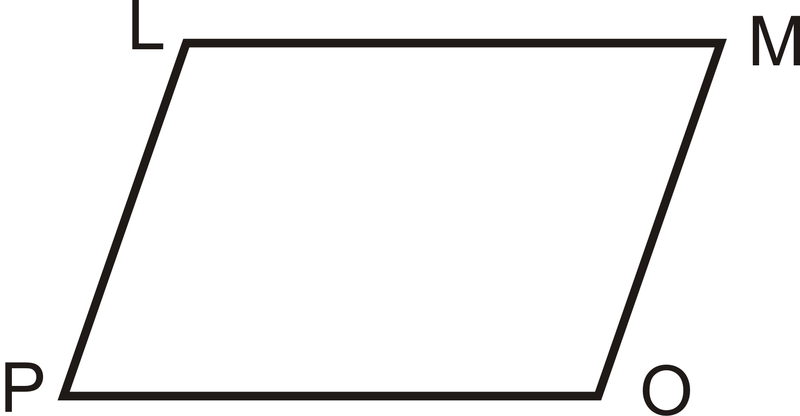
    Ф-Д_0Б4Д4Ф366Ф6Ф61КС07А6Д1ЦА84Е6 Бад С34318936С6А7919 FCE3D7BB1+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{10}\)
    Заява Причина
    1. 1.
    2. \(m\angle L=m\angle O\) 2.
    3. 3. Визначення додаткових кутів
    4. 4. Заміна
    5. 5. Заміна
    6. 6. Віднімання PoE
    7. \(\angle M\cong \angle P\) 7.
    1. Дано:\(\angle 1\cong \angle 4\)

    Доведіть:\(\angle 2\cong \angle 3\)

    Ф-Д_С1Е96Ф919536ДД8ДФ07Б0С96Ф91127C554C9АЦБ 470553431БД23D68+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{11}\)
    Заява Причина
    1. 1.
    2. \(m\angle 1=m\angle 4\) 2.
    3. 3. Визначення лінійної пари

    4. \(\angle 1\)і\(\angle 2\) є додатковими

    \(\angle 3\)і\(\angle 4\) є додатковими

    		 4.
    5. 5. Визначення додаткових кутів
    6. \(m\angle 1+m\angle 2=m\angle 3+m\angle 4\) 6.
    7. \(m\angle 1+m\angle 2=m\angle 3+m\angle 1\) 7.
    8. \(m\angle 2=m\angle 3\) 8.
    9. \(\angle 2\cong \angle 3\) 9.
    1. Дано:\(\angle C\) і\(\angle F\) є прямими кутами

    Доведіть:\(m\angle C+m\angle F=180^{\circ}\)

    Ф-Д_С1Е96Ф919536ДД8ДФ07Б0С96Ф91127C554C9АЦБ 470553431БД23D68+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{12}\)
    Заява Причина
    1. 1.
    2. \(m\angle C=90^{\circ}, \(m\angle F=90^{\circ}\) 2.
    3. \(90^{\circ}+90^{\circ}=180^{\circ}\) 3.
    4. \(m\angle C+m\angle F=180^{\circ}\) 4.
    1. Дано:\(l\perp m\)

    Доведіть:\(\angle 1\cong \angle 2\)

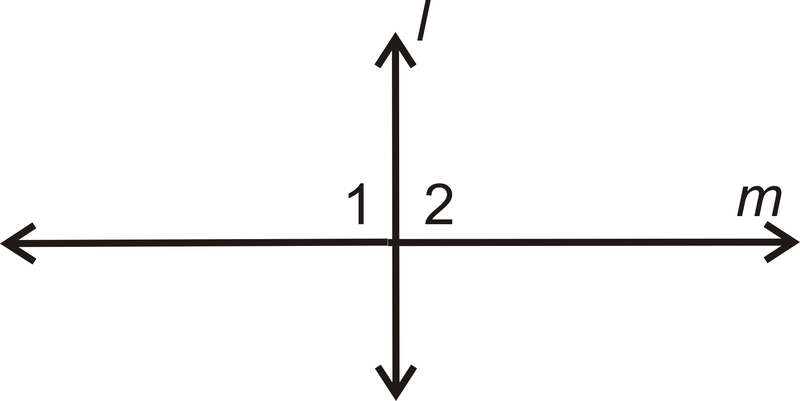
    Ф-Д_СЕ5Ф73109 АЦ53Ф5ДД286Ф7726АЕД 3АА0140С001АК 46667139BA4050+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{13}\)
    Заява Причина
    1. \(l\perp m\) 1.
    2. \(\angle 1\)і\(\angle 2\) є прямими кутами 2.
    3. 3.
    1. Дано:\(m\angle 1=90^{\circ}\)

    Доведіть:\(m\angle 2=90^{\circ}\)

    Ф-Д_СЕ5Ф73109 АЦ53Ф5ДД286Ф7726АЕД 3АА0140С001АК 46667139BA4050+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{14}\)
    Заява Причина
    1. 1.
    2. \(\angle 1\)і\(\angle 2\) є лінійною парою 2.
    3. 3. Постулат лінійної пари
    4. 4. Визначення додаткових кутів
    5. 5. Заміна
    6. \(m\angle 2=90^{\circ}\) 6.
    1. Дано:\(l\perp m\)

    Доведіть:\(\angle 1\) і\(\angle 2\) є доповненнями

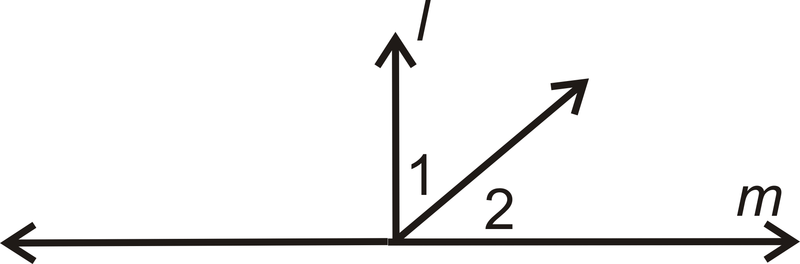
    Ф-Д_19042 ДК 8336С54С2Ф514 А7ФЕ224 БА4Е011С3Ф68АФБ 52Д610 Беб 138+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{15}\)
    Заява Причина
    1. 1.
    2. 2. \(\perp\)лінії створюють прямі кути
    3. \(m\angle 1+m\angle 2=90^{\circ}\) 3.
    4. \(\angle 1\)і\(\angle 2\) доповнюють 4.
    1. Дано:\(l\perp m\) і\(\angle 2\cong \angle 6\)

    Доведіть:\(\angle 6\cong \angle 5\)

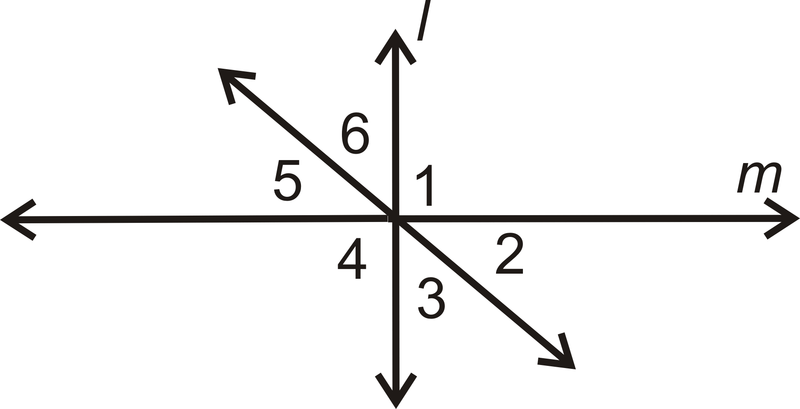
    Ф-Д_0А1Е84ФЦ5С3267С7ФД61С4636Д245ЕЕ72029Е0Е6971870Е44А0БФБ+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{16}\)
    Заява Причина
    1. 1.
    2. \(m\angle 2=m\angle 6\) 2.
    3. \(\angle 5\cong \angle 2\) 3.
    4. \(m\angle 5=m\angle 2\) 4.
    5. \(m\angle 5=m\angle 6\) 5.

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.7.

    Лексика

    Термін Визначення
    два стовпці докази Поширений спосіб організації доказу в геометрії. Два стовпці доказів завжди мають дві колонки- заяви і причини.
    лінійна пара Два кути утворюють лінійну пару, якщо вони є додатковими і сусідніми.

    Додаткові ресурси

    Відео: Принципи доказів двох стовпців - Основні

    Діяльність: Дві колонки Докази Дискусійні питання

    Навчальні посібники: Докази Навчальний посібник

    Практика: Вступ до доказів

    Реальний світ: Дайте мені одну причину