Skip to main content
LibreTexts - Ukrayinska

2.10: Негативні висловлювання

  1. Last updated
  2. Save as PDF
  • Page ID
    54527

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Значення істинності для заперечення умовних тверджень, сполучників і диз'юнкцій.

    У повсякденній мові негативні висловлювання часто неоднозначні або незрозумілі. Математично вам потрібен точний спосіб заперечувати твердження, щоб ви могли точно визначити, чи є твердження істинними чи хибними. Коли вірно заперечення наступного речення?

    Якщо мені не холодно, то сніг не йде.

    заперечення

    Хоча в повсякденній мові протилежністю «собака» може бути «кішка», в математиці протилежністю «собака» є «не собака». Використання слова «не» - основний спосіб звести нанівець атомне речення. Атомне речення - це логічне твердження без логічних зв'язків, що має істинне значення.

    • Оригінальне речення\((D)\): Ця річ - собака.
    • Заперечення речення\((\sim D)\): Ця річ не собака.

    Скринька нижче представляє всесвіт всіх речей. Цей Всесвіт можна розділити на речі, які є собаками, і речі, які не є собаками.

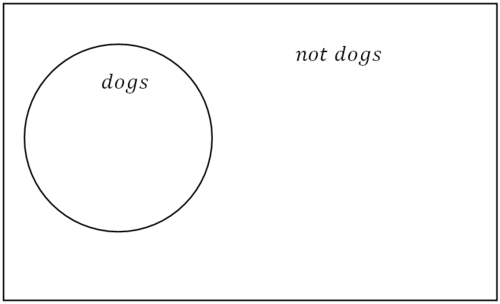    F-D_AE5C3190BDAD96074 DDC0AE9A862 ЕДБ3142СБ3Б194CB8EB1D90A59F+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{1}\)

    Щоб заперечувати складні твердження, які включають логічні зв'язки, такі як або, і, якщо-то, слід почати з побудови таблиці істинності та зауваження, що заперечення повністю перемикає значення істини.

    Заперечення умовного оператора вірно лише тоді, коли початковий оператор if-then є помилковим.

    \(P\) \(Q\) \(P \rightarrow Q\) \(\sim (P \rightarrow Q)\)
    Т Т Т F
    Т F F Т
    F Т Т F
    F F Т F

    Заперечення кон'юнкції є помилковим лише тоді, коли вихідні два твердження є істинними. Кон'юнкція - це два твердження, до яких приєднується «і».

    \(P\) \(Q\) \(P \wedge Q\) \(\sim (P \wedge Q)\)
    Т Т Т F
    Т F F Т
    F Т F Т
    F F F Т

    Заперечення диз'юнкції вірно лише тоді, коли обидва вихідних твердження є помилковими. Диз'юнкція - це два твердження, до яких приєднується «або».

    \(P\) \(Q\) \(P \lor Q\) \(\sim (P \lor Q)\)
    Т Т Т F
    Т F Т F
    F Т Т F
    F F F Т

    Теорія множин кола також може використовуватися для інтерпретації заперечення диз'юнкції або кон'юнкції.

    Затінена частина в полі представляє область, яка знаходиться всередині\(P\) або всередині\(Q\). Нагадаємо, що в математичній логіці це пишеться як\(P \lor Q\). У теорії множин ця область представлена аналогічно тому,\(P \cup Q\) де символ\(\cup\) означає об'єднання. Хоча позначення дещо відрізняються, міркування про відносини та наслідки ідентичні.

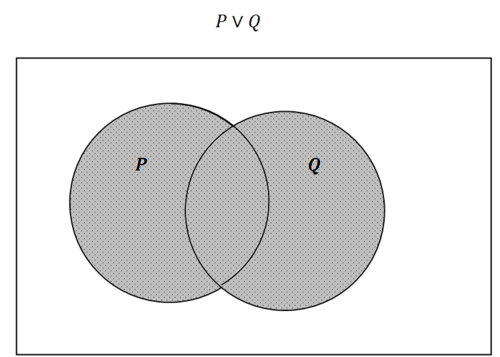    F-D_E72712DE1102F74AE5582D40B576EB7D9F9AAB03CFBED 2C3414D9+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{2}\)

    Коли ви скасовуєте твердження, ви повністю перемикаєте те, що затінено.

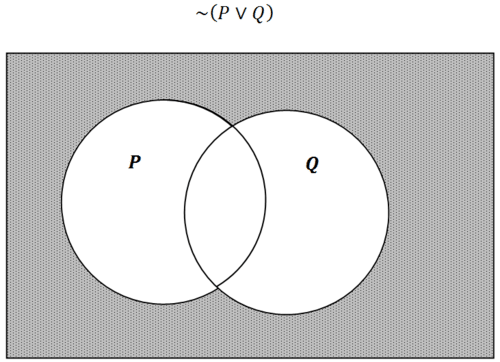    F-D_883687fc307956392250f5 подача 8E93bb00514c9195bbb8d21a314d15+зображення_thumb_поштова листівка_крихітка+зображення_thumb_листівка_крихітка_pngМалюнок\(\PageIndex{3}\)

    Інший спосіб думати про цю затінену область полягає в тому, що це регіон, який не знаходиться в P, а також не в Q. Це означає,\(\sim (P \lor Q)\) що еквівалентно\(\sim P \wedge \sim Q\).

    \(\sim (P \lor Q)\Leftrightarrow \sim P \wedge \sim Q\)

    Символ «\(\Leftrightarrow\)» працює в математичній логіці і теорії множин так само «\(=\)» працює в арифметиці та алгебрі. У цьому випадку негатив, здається, поширюється по всьому твердженню або, заперечуючи кожне твердження окремо і змінює твердження або на заяву і. Це називається Закон Де Моргана.

    Заперечення кон'юнкції дає аналогічний результат.

    Затінена частина в полі представляє область, яка знаходиться в межах P і всередині\(Q\). У математичній логіці це пишеться як\(P \wedge Q\). У теорії множин ця область представлена аналогічно тому\(P \cap Q\), де символ\(\cap\) позначає перетин. Як і раніше, позначення між математичною логікою і теорією множин дещо відрізняються. Однак міркування про відносини і логічні наслідки ідентичні.

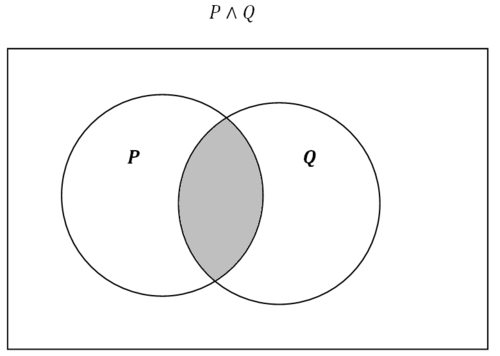    F-D_207d4d21d8EEBD8EBD8E11863A2B74978D2A9F782B813B21BD43+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{4}\)

    Коли ви скасовуєте твердження, ви повністю перемикаєте те, що затінено.

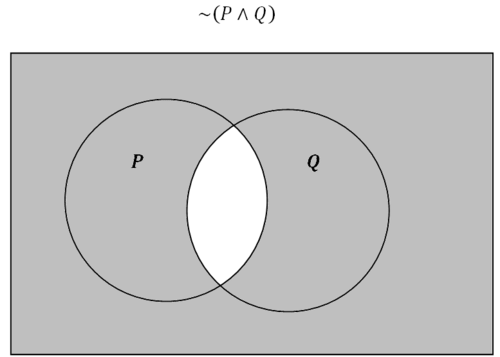    F-D_49194 Беб802ДФБ1705БФД58А10ДББ53БББ175cd9B1FE45D1123B67+зображення_thumb_поштова листівка_крихітка+зображення_великий палецька_поштова листівка_крихітка_pngМалюнок\(\PageIndex{5}\)

    Інший спосіб думати про цей затінений регіон - вважати, що він представляє все, що не знаходиться\(P\) або не знаходиться в\(Q\).

    \(\sim (P \wedge Q) \Leftrightarrow \sim P \lor \sim Q\)

    Це друге представництво Закону Де Моргана.

    Оскільки математичні речення стають більш складними з додатковими зв'язками, таблиці істинності та кола теорії набору є хорошими способами інтерпретації, коли твердження вірні і коли твердження помилкові.

    Приклад\(\PageIndex{1}\)

    Раніше вас запитали, коли істинно заперечення наступного твердження.

    Якщо мені не холодно, то сніг не йде.

    Твердження вже має кілька негативних частин, тому некоректно просто перемикати один або обидва заперечення.

    • \(P=I\: am\: cold.\)
    • \(Q=It\: is\: snowing.\)

    Рішення

    \(P\) \(Q\) \(\sim P\) \(\sim Q\) \(\sim P \rightarrow \sim Q\) \(\sim ( \sim P \rightarrow \sim Q)\)
    Т Т F F Т F
    Т F F Т Т F
    F Т Т F F Т
    F F Т Т Т F

    Почніть з побудови до вихідної заяви. Потім додайте стовпець, який повністю заперечує вихідне твердження. Зверніть увагу, що існує лише один рядок, де остаточне заперечене твердження є істинним. Тобто, коли\(P\) є помилковим і\(Q\) є істинним. Тому заперечення оригінального речення вірно, коли «мені не холодно» і «йде сніг».

    Приклад\(\PageIndex{2}\)

    Використовуйте кола теорії множин, щоб інтерпретувати заперечення умовного оператора і пояснити, як заперечення умовного може бути записано по-іншому.

    Рішення

    Затінена частина у полі представляє область, яка робить таке твердження істинним.

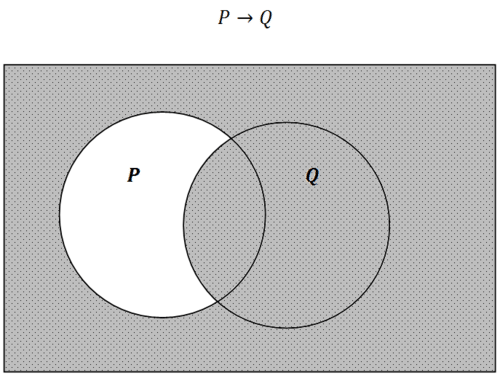    F-D_CC6E97aa723E7C03a8397abe00b8957CBB5ad1894F22a76DD83CB+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_поштова листівка_крихітка_pngМалюнок\(\PageIndex{6}\)

    Зверніть увагу, що на діаграмі Венна є чотири різні регіони, які відповідають чотирьом різним рядкам таблиці умовної істинності. Єдиний простір, який не робить твердження істинним, -\(P\) це коли true (всередині кола\(P\)) і\(Q\) є помилковим (зовнішнє коло\(Q\)).

    \(P\) \(Q\) \(P \rightarrow Q\)
    Т Т Т
    Т F F
    F Т Т
    F F Т

    Щоб скасувати це твердження, ви перемикаєте значення в таблиці істинності та перемикаєте затінену область на діаграмі Венна.

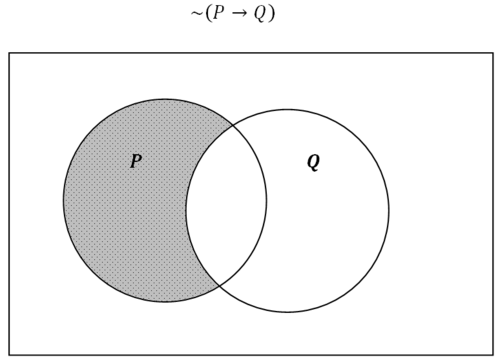    F-D_E64 FF75CB73AF62789A951A60EAFF9277E926830F8515CD9ADBC6C4+зображення_thumb_поштова листівка_крихітка+зображення_великий палець_листівка_крихітка_pngМалюнок\(\PageIndex{7}\)

    Інший спосіб думати про цю затінену область - це сприймати його як простір, який знаходиться,\(P\) але не в ньому\(Q\).

    \(\sim (P \rightarrow Q) \Leftrightarrow P \wedge \sim Q\)

    Приклад\(\PageIndex{3}\)

    Показати, що наступні твердження еквівалентні в таблиці істинності. Символ\(\equiv\) означає еквівалент. Бути рівнозначним у цьому випадку означає бути істинним одночасно і помилковим одночасно.

    \(P \wedge Q \equiv \sim ( \sim P \lor \sim Q)\)

    Рішення

    Хоча таблиця істини не є доказом, вона може допомогти вам розпізнати, коли два твердження мають однакові значення істини.

    \(P\) \(Q\) \(\sim P\) \(\sim Q\) \(\sim P \lor \sim Q\) \(\sim ( \sim P \lor \sim Q)\) \(P \wedge Q\)
    Т Т F F F Т Т
    Т F F Т Т F F
    F Т Т F Т F F
    F F Т Т Т F F

    Зверніть увагу, що останні два стовпці ідентичні.

    Приклад\(\PageIndex{4}\)

    Напишіть речення двома різними способами, ілюструючи математичне твердження в прикладі 3

    Рішення

    \(P \wedge Q\): Мені подобаються фільми і я люблю телевізор. \(\sim ( \sim P \lor \sim Q)\): Це не так, що або мені не подобаються фільми, або мені не подобається телевізор.

    Приклад\(\PageIndex{5}\)

    Тавтологія - це логічне твердження, яке завжди вірно. Продемонструйте наступну тавтологію в таблиці істинності.

    \(B \rightarrow (A \lor \sim A)\)

    Рішення

    \(A\) \(\sim A\) \(B\) \(A \lor \sim A\) \(B \rightarrow (A \lor \sim A)\)
    Т F F Т Т
    Т F Т Т Т
    F Т Т Т Т
    F Т F Т Т

    Зверніть увагу, що останній стовпець - це всі T. Це означає, що це твердження завжди вірно і тому є тавтологією.

    Рецензія

    Наступні вихідні я збираюся покататися на лижах або сноуборді.

    1. Визначте атомні висловлювання у наведеному вище реченні та використовуйте логічні зв'язки, щоб переписати речення символами.

    2. Напишіть заперечення пропозиції символами і запишіть заперечення пропозиції словами природним чином.

    Майк і Джон обидва пообідали зі мною.

    3. Визначте атомні висловлювання у наведеному вище реченні та використовуйте логічні зв'язки, щоб переписати речення символами.

    4. Напишіть заперечення пропозиції символами і запишіть заперечення пропозиції словами природним чином.

    Ні мій брат, ні сестра не хочуть грати зі мною.

    5. Визначте атомні висловлювання у наведеному вище реченні та використовуйте логічні зв'язки, щоб переписати речення символами.

    6. Напишіть заперечення пропозиції символами і запишіть заперечення пропозиції словами природним чином.

    Напишіть заперечення для наступних тверджень.

    7. Всі собаки йдуть на небеса.

    8. Мій вчитель рідко помиляється.

    9. Всі люблять піцу.

    Складіть таблиці істинності для кожного з наступних.

    10. \((P \wedge Q) \lor \sim Q\)

    11. \(P \wedge (Q \lor \sim Q)\)

    12. \((P \lor Q) \lor \sim R\)

    13. \(( \sim P \wedge \sim Q) \lor \sim R\)

    14. Яке найпростіше твердження, еквівалентне #11:\(P \wedge (Q \lor \sim Q)\)?

    15. Використовуйте Закон Де Моргана, щоб знайти твердження, еквівалентне наступному твердженню:\(\sim (Q \lor \sim Q)\)

    16. Використовуйте Закон Де Моргана, щоб знайти твердження, еквівалентне наступному твердженню:\(\sim (P \lor Q) \lor \sim R\)

    Лексика

    Термін Визначення
    атомний заяву Атомний оператор - це декларативне твердження без логічних зв'язків, що має значення істинності.
    сполучник Кон'юнкція - це твердження «і», яке є твердженням, яке поєднує в собі два логічних твердження і вірно лише тоді, коли обидва твердження вірні. Символ «і» - «\(\wedge\)».
    Закон Де Моргана Закон Де Моргана перетворює кон'юнкцію в диз'юнкцію за допомогою заперечення.
    диз'юнкція Диз'юнкція - це твердження «або», яке поєднує в собі два логічних твердження, і є хибним лише тоді, коли обидва твердження є помилковими. Символ «або» - «\(\lor\)».
    заперечення Заперечення заяви є протилежним твердженню. Якщо вихідне твердження є\(D\), то заперечення твердження представлено\(\sim D\). Твердження і його заперечення завжди матимуть протилежні значення істини.
    тавтологія Тавтологія - це логічне твердження, яке завжди вірно. Тавтологія - це тип основної теореми.

    Додатковий ресурс

    Практика: Негативні висловлювання