Skip to main content
LibreTexts - Ukrayinska

2.6: Гіпотези та зустрічні приклади

  1. Last updated
  2. Save as PDF
  • Page ID
    54573

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Освічені здогади і приклади, які їх спростовують.

    Гіпотеза - це «освічена здогадка», яка базується на прикладах у шаблоні. Контрприклад - приклад, який спростовує гіпотезу.

    Припустимо, вам дали математичну схему на кшталт\(h = \dfrac{−16}{t^2}\). Що робити, якщо ви хотіли зробити освічену здогадку, або здогадки, про\(h\)?

    Використовуйте наступну інформацію для прикладів 1 та 2:

    Продавець автомобілів продав 5 старих автомобілів п'яти різним парам. Він помітив, що кожній парі не виповнилося 30 років. Наступного дня він продав новий, розкішний автомобіль парі в 60-х роках, продавець визначив, що тільки молоді пари вживаних автомобілів.

    Приклад\(\PageIndex{1}\)

    Чи логічна здогадка продавця? Чому чи чому ні?

    Рішення

    Це логічно, засноване на його переживаннях, але не відповідає дійсності.

    Приклад\(\PageIndex{2}\)

    Чи можете ви придумати контрприклад?

    Рішення

    Контрприкладом буде пара, яка 30 років або старше, купуючи вживаний автомобіль.

    Приклад\(\PageIndex{3}\)

    Ось алгебраїчне рівняння і таблиця значень для\(n\) і\(t\).

    \(t=(n−1)(n−2)(n−3)\)

    \(n\) \((n−1)(n−2)(n−3)\) \(t\)
    \ (n\)» клас ="lt-k12-2141">1 \ ((n−1) (n−2) (n−3)\)» клас ="lt-k12-2141">\((0)(−1)(−2)\) \ (t\)» клас = "lt-k12-2141">0
    \ (n\)» клас = "lt-k12-2141">2 \ ((n−1) (n−2) (n−3)\)» клас ="lt-k12-2141">\((1)(0)(−1)\) \ (t\)» клас = "lt-k12-2141">0
    \ (n\)» клас = "lt-k12-2141">3 \ ((n−1) (n−2) (n−3)\)» клас ="lt-k12-2141">\((2)(1)(0)\) \ (t\)» клас = "lt-k12-2141">0

    Рішення

    Подивившись на стіл, Пабло робить таку здогаду:

    Значення\((n−1)(n−2)(n−3)\) 0 для будь-якого числа n.

    Це справжня здогадка?

    Це не є дійсною здогадкою. Якби Пабло продовжив таблицю до n = 4, він би побачив, що\((n−1)(n−2)(n−3)=(4−1)(4−2)(4−3)=(3)(2)(1)=6\)

    В даному прикладі\(n=4\) наведено контрприклад.

    Приклад\(\PageIndex{4}\)

    Артур робить фігури для арт-проекту. Він намалював багатокутники і деякі їх діагоналі.

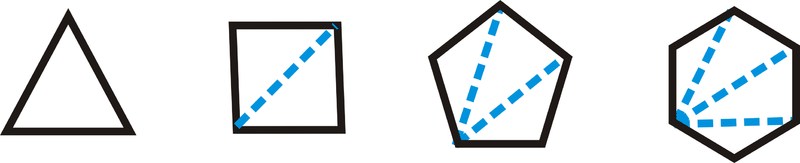
    F-D_1A8E 170ААФ 8620 ЕАФ 6Б280 АДЕК 82dced4A1087956F5EA32A28204C7F+зображення_крихіткий+зображення_крихіткий.PNG
    Малюнок\(\PageIndex{1}\)

    З цих прикладів Артур зробив таку здогаду:

    Якщо опуклий багатокутник має\(n\) сторони, то утворюються\(n−2\) трикутники, що утворюються при проведенні діагоналей від будь-якої вершини багатокутника.

    Чи правильна гіпотеза Артура? Або, можете знайти контрприклад?

    Рішення

    Здогадка видається правильною. Якщо Артур малює інші багатокутники, у кожному випадку він зможе малювати\(n−2\) трикутники, якщо багатокутник має n сторін.

    Зверніть увагу, що ми не довели гіпотезу Артура, а лише знайшли кілька прикладів, які відповідають дійсності. Отже, на цьому етапі ми говоримо, що гіпотеза вірна.

    Приклад\(\PageIndex{5}\)

    Наведіть контрприклад цього твердження: Кожне просте число є непарним числом.

    Рішення

    Єдиним зустрічним прикладом є число 2: парне число (не непарне), яке є простим.

    Рецензія

    Наведіть контрприклад для кожного з наступних тверджень.

    1. Якщо\(n\) ціле число, то\(n^2 >n\).
    2. Усі числа, що закінчуються на 1, є простими числами.
    3. Всі позитивні дроби знаходяться в межах від 0 до 1.
    4. Будь-які три точки, які є компланарними, також є колінеарними.
    5. Всі дівчата люблять морозиво.
    6. Всі старшокласники перебувають у хорі.
    7. Для будь-якого кута існує додатковий кут.
    8. Всі підлітки можуть керувати автомобілем.
    9. Якщо\(n\) ціле число, то\(n>0\).
    10. Всі рівняння мають цілочисельні рішення.

    Огляд (Відповіді)

    Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.5.

    Ресурси

    Лексика

    Термін Визначення
    здогадки Гіпотеза - це освічена здогадка, яка базується на прикладах у шаблоні.
    контрприклад Контрприклад - приклад, який спростовує гіпотезу.
    фракція Дріб - це частина цілого. Дріб записується математично як одне значення поверх іншого, відокремлене бруском дробу. Його ще називають раціональним числом.

    Додаткові ресурси

    Інтерактивний елемент

    Відео: Індуктивні міркування

    Діяльність: Гіпотези та зустрічні приклади Дискусійні питання

    Навчальні посібники: типи міркувань навчальний посібник

    Практика: здогадки та контрприклади

    Реальний світ: здогадки та контрприклади