2.8: Таблиці істинності

Last updated
Save as PDF

Page ID: 54584

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Поки ми знаємо ці символи для логіки:

\(\sim\)not (заперечення)
\(\rightarrow\)якби то
\(\therefore\)тому

Ще два символи:

\(\wedge\)і
\(\lor\)або

Ми б писали «\(p\)і\(q\)» як\(p\wedge q\) і «\(p\)або\(q\)» як\(p\lor q\).

Таблиці істинності використовують ці символи і є ще одним способом аналізу логіки. Для початку давайте зв'яжемо p і\ sim p Щоб було простіше, встановіть p як: парне число. Тому\ sim p - непарне число. Складіть таблицю правди, щоб з'ясувати, чи є вони обома правдивими. Починають з усіх «істин» p, true (T) або false (F).

р
Т
F

Далі пишемо відповідні значення істинності для\(\sim p\). \(\sim p\)має протилежні значення істини\(p\). Отже, якщо\(p\) правда, то\(\sim p\) є помилковим і навпаки.

р	\ Сім п
Т	F
F	Т

Щоб підвести підсумок:

Почніть таблиці істинності з усіма можливими комбінаціями істин. Для 2 змінних є 4 комбінації для 3 змінних є 8. Ви завжди починаєте таблицю правди таким чином.
Робіть будь-які заперечення на будь-яку зі змінних.
Виконайте будь-які комбінації в дужках.
Закінчіть з завершенням того, про що просила проблема.

Малювання таблиці істинності

1. Намалюйте таблицю істинності для\(p\),\(q\) і\(p \wedge q\).

Спочатку зробіть стовпці для p і q. заповніть стовпці всіма можливими істинними і хибними комбінаціями для двох.

р	q
Т	Т
Т	F
F	Т
F	F

Зверніть увагу на всі комбінації р і q У будь-який час у нас є таблиці істини з двома змінними, це завжди, як ми заповнюємо перші два стовпці.

Далі нам потрібно з'ясувати, коли\(p\wedge q\) істинно, виходячи з перших двох стовпців. p\ клин q може бути істинним, тільки якщо обидва p і q є істинними. Отже, заповнена таблиця виглядає наступним чином:

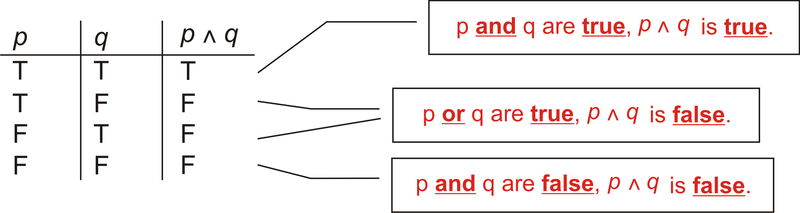F-D_B2B66563E17A9E7BE0769A81E23555C42Ф9447А8Б6 АФБА 5C59A0C06+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{1}\)

Ось так завжди заповнюється таблиця істинності з двома змінними та їх стовпцем «і».

2. Намалюйте таблицю істинності для\(p\),\(q\) і\(p \lor q\).

Спочатку створимо стовпці для\(p \lor q\) і\(q\), як і приклад А.

р	q
Т	Т
Т	F
F	Т
F	F

Далі нам потрібно з'ясувати, коли\(p \lor q\) це правда, виходячи з перших двох стовпців. \(p \lor q\)є істинним, якщо\(p\) АБО\(q\) є істинними, або обидва є істинними. Отже, заповнена таблиця виглядає наступним чином:

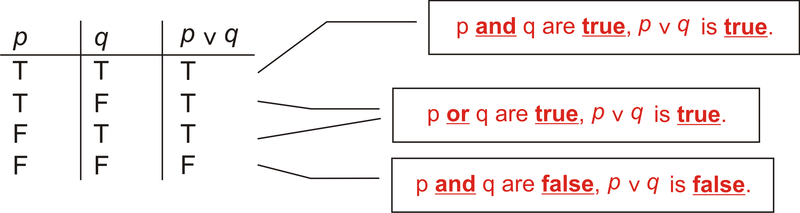F-д_Ф8Б2АФ 3А483387836765 ФА06А98А5ЕФ ФС397Б752608ЕФ4Ф947790+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок\(\PageIndex{2}\)

Різниця між\(p \wedge q\) і\(p \lor q\) є другим і третім рядами. Бо «і» обидва\(p\) і\(q\) повинні бути правдою, але для «або» тільки один повинен бути правдою.

Визначення істин змінних

Визначте істини для\(p \wedge(\sim q \lor r)\).

По-перше, є три змінні, тому ми будемо потрібні всі комбінації їх істин. Для трьох змінних завжди існує 8 можливих комбінацій.

\(p\)	\(q\)	\(r\)
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">Т
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">F
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">Т
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">F
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">Т
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">F
\ (p\) ">F	\ (q\) ">F	\ (r\) ">Т
\ (p\) ">F	\ (q\) ">F	\ (r\) ">F

Далі звертайтеся за адресою\(\sim q\). Це якраз і будуть протилежності\(q\) колони.

\(p\)	\(q\)	\(r\)	\(\sim q\)
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F
\ (p\) ">F	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т
\ (p\) ">F	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т

Тепер давайте зробимо те, що в дужках,\(\sim q\lor r\). Пам'ятайте, для «або» тільки\(\sim q\) АБО\(r\) має бути правдою. Використовуйте лише\(r\) стовпці\(\sim q\) та для визначення значень у цьому стовпці.

\(p\)	\(q\)	\(r\)	\(\sim q\)	\(\sim q\lor r\)
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F	\ (\ sim q\ lor r\) ">Т
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F	\ (\ sim q\ або r\) ">F
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F	\ (\ sim q\ lor r\) ">Т
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F	\ (\ sim q\ або r\) ">F
\ (p\) ">F	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т
\ (p\) ">F	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т

Нарешті, ми можемо вирішити всю проблему,\(p \wedge(\sim q \lor r)\). Використовуйте\(p\) і\(\sim q\lor r\) для визначення значень. Пам'ятайте, для «і» обох\(p\) і\(\sim q\lor r\) повинні бути правдою.

\(p\)	\(q\)	\(r\)	\(\sim q\)	\(\sim q\lor r\)	\(p \wedge(\sim q \lor r)\)
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">T
\ (p\) ">Т	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F	\ (\ sim q\ або r\) ">F	\ (p\ клин (\ sim q\ lor r)\) ">F
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">T
\ (p\) ">Т	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">T
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">Т	\ (\ sim q\) ">F	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">F
\ (p\) ">F	\ (q\) ">Т	\ (r\) ">F	\ (\ sim q\) ">F	\ (\ sim q\ або r\) ">F	\ (p\ клин (\ sim q\ lor r)\) ">F
\ (p\) ">F	\ (q\) ">F	\ (r\) ">Т	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">F
\ (p\) ">F	\ (q\) ">F	\ (r\) ">F	\ (\ sim q\) ">Т	\ (\ sim q\ lor r\) ">Т	\ (p\ клин (\ sim q\ lor r)\) ">F

Напишіть таблицю істинності для наступних змінних.

Приклад\(\PageIndex{1}\)

\(p \wedge \sim p\)

Рішення

Спочатку зробіть стовпці для\(p\), потім додайте\(\sim p\) і, нарешті, оцініть\(p \wedge \sim p\).

\(p\)	\(\sim p\)	\(p \wedge \sim p\)
\ (p\) ">Т	\ (\ sim p\) ">F	\ (p\ клин\ сім р\) ">F
\ (p\) ">F	\ (\ sim p\) ">Т	\ (p\ клин\ сім р\) ">F

Приклад\(\PageIndex{2}\)

\(\sim p \lor \sim q\)

Рішення

Спочатку зробіть стовпці для\(p\) і\(q\), потім додайте в\(\sim p\) і\(\sim q\). Нарешті, оцініть\(\sim p \lor \sim q\).

\(p\)	\(q\)	\(\sim p\)	\(\sim q\)	\(\sim p \lor \sim q\)
\ (p\) ">\(p \lor \sim q\)	\ (q\) ">Т	\ (\ sim p\) ">F	\ (\ sim q\) ">F	\ (\ sim p\ lor\ sim q\) ">F
\ (p\) ">Т	\ (q\) ">F	\ (\ sim p\) ">F	\ (\ sim q\) ">Т	\ (\ sim p\ lor\ sim q\) ">T
\ (p\) ">F	\ (q\) ">Т	\ (\ sim p\) ">Т	\ (\ sim q\) ">F	\ (\ sim p\ lor\ sim q\) ">T
\ (p\) ">F	\ (q\) ">F	\ (\ sim p\) ">Т	\ (\ sim q\) ">Т	\ (\ sim p\ lor\ sim q\) ">T

Приклад\(\PageIndex{3}\)

\(p \wedge (q\lor \sim q)\)

Рішення

Спочатку зробіть стовпчики для p і q, потім додайте в\(\sim q\) і\(q\lor \sim q\). Нарешті, оцініть\(p\wedge (q\lor \sim q)\).

\(p\)	\(q\)	\(\sim q\)	\(q\lor \sim q\)	\(p\wedge (q\lor \sim q)\)
\ (p\) ">Т	\ (q\) ">Т	\ (\ sim q\) ">F	\ (q\ lor\ сім q\) ">T	\ (p\ клин (q\ lor\ sim q)\) ">T
\ (p\) ">Т	\ (q\) ">F	\ (\ sim q\) ">Т	\ (q\ lor\ сім q\) ">T	\ (p\ клин (q\ lor\ sim q)\) ">T
\ (p\) ">F	\ (q\) ">Т	\ (\ sim q\) ">F	\ (q\ lor\ сім q\) ">T	\ (p\ клин (q\ lor\ sim q)\) ">F
\ (p\) ">F	\ (q\) ">F	\ (\ sim q\) ">Т	\ (q\ lor\ сім q\) ">T	\ (p\ клин (q\ lor\ sim q)\) ">F

Рецензія

Напишіть таблицю істинності для наступних змінних.

\((p \wedge q)\lor \sim r\)
\(p \lor ( \sim q \lor r)\)
\(p \wedge (q \lor \sim r)\)
Єдина відмінність між #1 і #3 полягає в розміщенні дужок. Чим відрізняються таблиці істинності?
Коли це\(p \lor q \lor r\) правда?
\(p \lor q \lor r\)
\((p \lor q) \lor \sim r\)
\(( \sim p \wedge \sim q) \wedge r\)
\(( \sim p \lor \sim q) \wedge r\)

Чи є наступне вагомим аргументом? Якщо так, то який закон використовується? ПІДКАЗКА: Заяви можуть вийти з ладу.

\(p \rightarrow q\)

\(r \rightarrow p\)

\(\therefore r \rightarrow q\)

\(p \rightarrow q\)

\(r \rightarrow q\)

\(\therefore p \rightarrow r\)

\(p \rightarrow \sim r\)

\(r \)

\(\therefore \sim p\)

\(\sim q \rightarrow r\)

\(q \)

\(\therefore \sim r\)

\(p \rightarrow (r \rightarrow s)\)

\(p \)

\(\therefore r \rightarrow s\)

\(r \rightarrow q\)

\(r \rightarrow s \)

\(\therefore q \rightarrow s\)

Додаткові ресурси

Відео: Принципи таблиць істинності

Практика: Таблиці істинності