2.5: Індуктивні міркування з шаблонів

Last updated

Oct 27, 2022
Save as PDF
- 2.4: Типи міркувань
- 2.6: Гіпотези та зустрічні приклади

$\newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} }$

$\newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\id}{\mathrm{id}}$

$\newcommand{\Span}{\mathrm{span}}$

$\newcommand{\kernel}{\mathrm{null}\,}$

$\newcommand{\range}{\mathrm{range}\,}$

$\newcommand{\RealPart}{\mathrm{Re}}$

$\newcommand{\ImaginaryPart}{\mathrm{Im}}$

$\newcommand{\Argument}{\mathrm{Arg}}$

$\newcommand{\norm}[1]{\| #1 \|}$

$\newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$\newcommand{\Span}{\mathrm{span}}$

Індуктивні міркування

Одним з видів міркувань є індуктивні міркування. Індуктивне міркування тягне за собою робити висновки на основі прикладів і закономірностей. Візуальні шаблони та числові моделі дають хороші приклади індуктивних міркувань. Давайте розглянемо деякі закономірності, щоб зрозуміти, що таке індуктивні міркування.

Що робити, якщо вам дали візерунок з трьох чисел або фігур і попросили визначити шосте число або форму, яка відповідає цьому малюнку?

Приклад $\PageIndex{1}$

Крапковий візерунок показаний нижче. Скільки точок було б на $4^{th}$ малюнку? Скільки точок було б на $6^{th}$ малюнку?

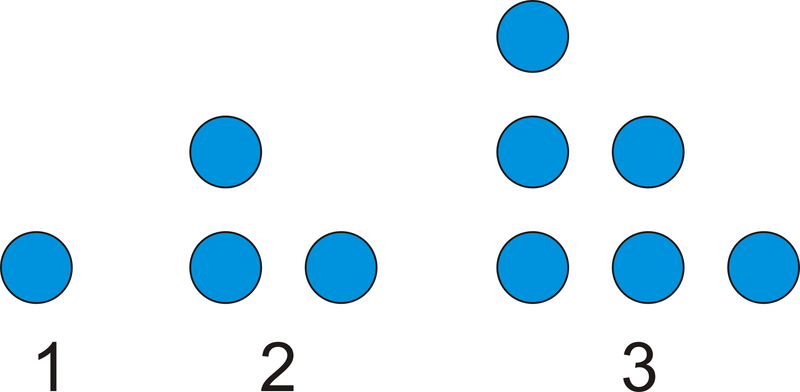Ф-д_5Ф28АФ9А1387Б192Е21Д0АБЕК 0782Ф00374А18841Ф87C24FF1FF235+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{1}$

Рішення

Намалюйте малюнок. Підраховуючи точки, є $4+3+2+1=10$ точки.

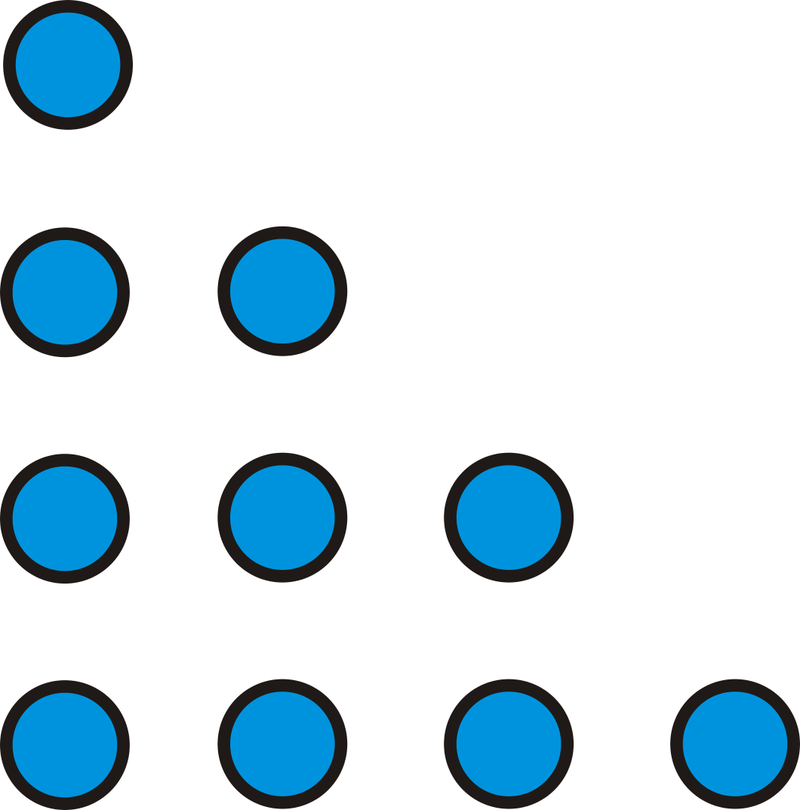F-D_E598B4 Беа А0Д3Е0ФД168 ДД7 КБД1С6 БФ А2ФА187 А97Д6ФБ905Д83+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{2}$

Для $6^{th}$ фігури ми можемо використовувати той же візерунок, $6+5+4+3+2+1$ . На $6^{th}$ малюнку 21 крапка.

Приклад $\PageIndex{2}$

Скільки трикутників було б на $10^{th}$ малюнку?

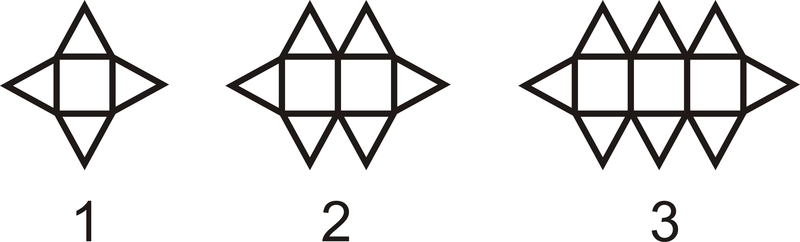F-д_Е6 Фе 357 ДБФ де 893328 ББ8Е809Е234Е10А7ДД9Д2А11Е9Ф3С04037858+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{3}$

Рішення

На $10^{th}$ малюнку було б 10 квадратів, з трикутником вище і нижче кожного. Також на кожному кінці фігури є трикутник. Це робить $10+10+2=22$ трикутники у всіх.

Приклад $\PageIndex{3}$

Подивіться на візерунок $2, 4, 6, 8, 10, \ldots$ Що таке $19^{th}$ термін у викрійці?

Рішення

Кожен термін на 2 більше, ніж попередній термін.

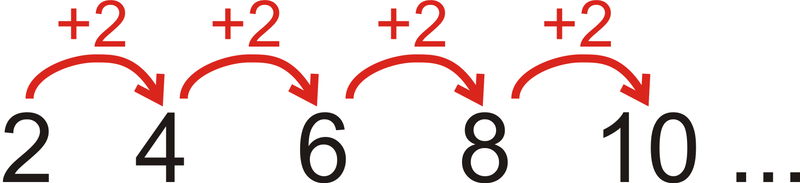Ф-д_ад 6Б5Е85А1АААА3 А46Е 0502 АААФ 30095Е6ДБ3Е490БК4235А8+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{4}$

Ви могли б порахувати шаблон до $19^{th}$ терміну, але це може зайняти деякий час. Зверніть увагу, що $1^{st}$ термін є $2 \cdot 1$ , 2-й термін - це $2 \cdot 2$ , 3-й термін - $2 \cdot 3$ і так далі. Отже, $19^{th}$ термін був би $2 \cdot 19$ або 38.

Приклад $\PageIndex{4}$

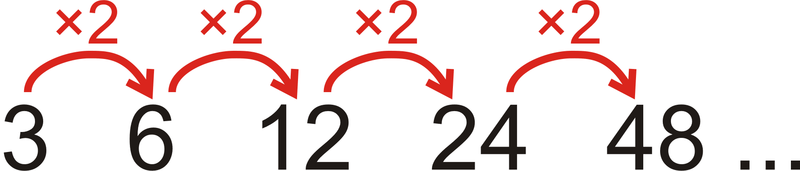
Подивіться на викрійку: $3, 6, 12, 24, 48, \ldots$

Який наступний термін у шаблоні? Що таке $10^{th}$ термін?

Рішення

Кожен член множиться на 2, щоб отримати наступний термін.

F-D_335655172E89D5550E8D04D9E3D938811D3Б 40117ФД7Ф5482Ф2С+зображення_крихіткий+зображення_крихіткий.PNG — Малюнок $\PageIndex{5}$

Тому наступний термін буде $48 \cdot 2$ або 96.

Щоб знайти $10^{th}$ термін, продовжуйте множити на 2, або $3\cdot \underbrace{2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2 \cdot 2 }_{2^{9}}=1536$ .

Приклад $\PageIndex{5}$

Знайдіть 8-й термін у списку чисел: $2, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots$

Рішення

Спочатку змініть 2 на дріб, або $\dfrac{2}{1}$ . Отже, візерунок тепер $\dfrac{2}{1}, \dfrac{3}{4}, \dfrac{4}{9}, \dfrac{5}{16}, \dfrac{6}{25}\ldots$ Верх є $2, 3, 4, 5, 6$ . Він щоразу збільшується на 1, тому чисельник $8^{th}$ терміна дорівнює 9. Знаменниками є квадратні числа, тому знаменник $8^{th}$ терміна дорівнює $8^2$ або 64. $8^{th}$ Термін є $\dfrac{9}{64}$ .

Рецензія

Для питань 1-3 визначте, скільки точок буде в $4^{th}$ і $10^{th}$ візерунок кожного малюнка нижче.

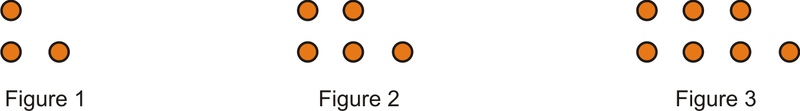Малюнок $\PageIndex{6}$
Малюнок $\PageIndex{7}$
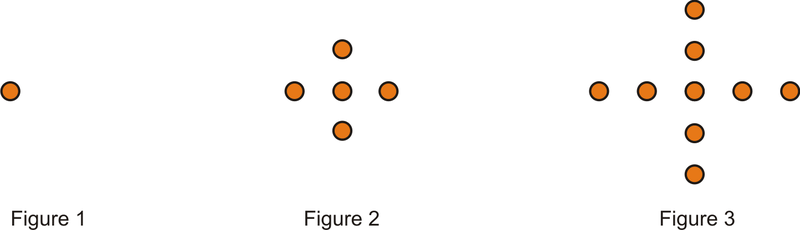
Малюнок $\PageIndex{8}$
Скористайтеся шаблоном нижче, щоб відповісти на питання.

Малюнок $\PageIndex{9}$
1. Намалюйте наступну фігуру в викрійці.
2. Як число точок у кожній зірці співвідноситься з номером фігури?
Скористайтеся шаблоном нижче, щоб відповісти на питання. Всі трикутники - це рівносторонні трикутники.

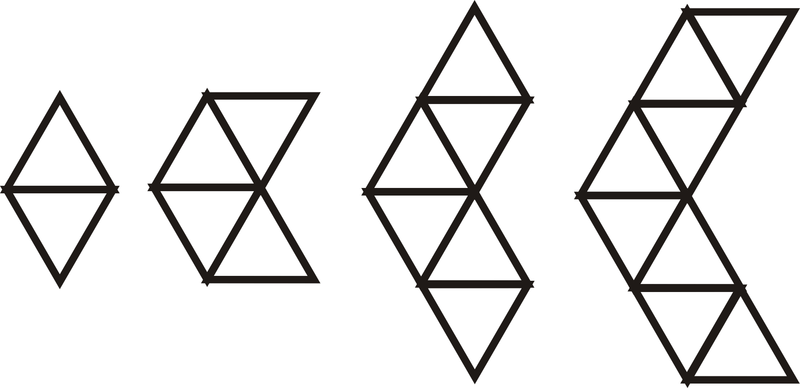Малюнок $\PageIndex{10}$
1. Намалюйте наступну фігуру в викрійці. Скільки трикутників у нього?
2. Визначте, скільки трикутників на $24^{th}$ малюнку.

Для питань 6-13 визначте: наступні три терміни в викрійці.

$5, 8, 11, 14, 17, \ldots$
$6, 1, -4, -9, -14, \ldots$
$2, 4, 8, 16, 32, \ldots$
$67, 56, 45, 34, 23, \ldots$
$9, -4, 6, -8, 3, \ldots$
$\dfrac{1}{2}, \dfrac{2}{3}, \dfrac{3}{4}, \dfrac{4}{5}, \dfrac{5}{6}, \ldots$
$\dfrac{2}{3}, \dfrac{4}{7}, \dfrac{6}{11},\dfrac{8}{15}, \dfrac{10}{19},\ldots$
$-1, 5, -9, 13, -17, \ldots$

Для питань 14-17 визначте наступні два терміни і опишіть закономірність.

$3, 6, 11, 18, 27, \ldots$
$3, 8, 15, 24, 35, \ldots$
$1, 8, 27, 64, 125, \ldots$
$1, 1, 2, 3, 5, \ldots$

Огляд (Відповіді)

Щоб переглянути відповіді на огляд, відкрийте цей PDF-файл і знайдіть розділ 2.1.

Лексика

Термін	Визначення
Індуктивні міркування	Індуктивні міркування - це тип міркування, де можна зробити висновки з шаблонів та попередніх прикладів.
Рівносторонній трикутник	Рівносторонній трикутник - це трикутник, у якого всі три сторони мають однакову довжину.

Додаткові ресурси

Інтерактивний елемент

Відео: Індуктивні міркування

Діяльність: Індуктивні міркування з питань обговорення шаблонів

Навчальні посібники: типи міркувань навчальний посібник

Практика: Індуктивні міркування з шаблонів

Реальний світ: наука про індукцію