3.6: Категоричні силогізми

Як ми вже говорили, Aristotelian Logic обмежується оцінкою аргументів, всі пропозиції яких - передумови та висновки - є категоричними. Є ще одне обмеження: Аристотельська логіка оцінює лише категоричні силогізми. Це особливий вид аргументу, що відповідає наступним умовам:

Категоричний силогізм - це дедуктивний аргумент, що складається з трьох категоріальних пропозицій (двох передумов і висновку); в сукупності ці три пропозиції мають рівно три класи; кожен з трьох класів зустрічається рівно в двох з пропозицій.

Це рот, але приклад дасть зрозуміти. Ось такий (дурний) категоричний силогізм:

Всі бурундуки - республіканці.
Деякі республіканці є гравцями в гольф.
Тому деякі бурундуки є гравцями в гольф.

Цей аргумент відповідає умовам у визначенні: він має три пропозиції; задіяні рівно три класи (бурундуки, республіканці та гравці в гольф); і кожен з трьох класів зустрічається рівно в двох з пропозицій (перевірте це і дивіться).

Існує певна спеціальна термінологія для класових термінів і приміщень в категоричних силогізмах. Кожен з трьох класових термінів має спеціальне позначення. Так званий основний термін термін, який з'являється в присудок положення в висновку; в нашому дурному прикладі, що 's' гольфістів'. Мінорний термін - це термін, який фігурує в предметній позиції у висновку; у нашому прикладі це «бурундуки». Середній термін - це інший, той, який з'являється в кожному з приміщень; у нашому прикладі це «республіканці».

Приміщення також мають спеціальні позначення. Основна передумова є той, який має основний термін в ньому; в нашому прикладі, що 's' s Деякі республіканці є гравцями в гольфі'. Незначна передумова - це інша, та, що містить незначний термін; у нашому прикладі це «Усі бурундуки - республіканці».

Остаточне обмеження: категоричні силогізми повинні бути написані в стандартній формі. Це означає перерахування приміщень у правильному порядку, з основним приміщенням першим, а другорядним приміщенням другого. Якщо ви подивитеся на наш дурний приклад, то зауважте, що він не в стандартному вигляді. Щоб її закріпити, нам потрібно змінити порядок приміщень:

Деякі республіканці є гравцями в гольф.
Всі бурундуки - республіканці.
Тому деякі бурундуки є гравцями в гольф.

На цьому етапі може виникнути старе занепокоєння: обмежуючись таким обмеженим класом аргументів, чи не ризикує Аристотелівська логіка не бути в змозі оцінити багато реальних аргументів, про які нас хвилюють? Відповідь на це занепокоєння залишається незмінною: хоча більшість (майже всі) реальні аргументи не представлені як стандартна форма категоричних силогізмів, дивовижна кількість з них може бути переведена в цю форму. Наприклад, аргументи з більш ніж двома передумовами можуть бути переписані як ланцюжки суб-аргументів з двома передумовами. Як і у випадку, коли ми підняли цю стурбованість раніше, ми відкинемо брудні деталі того, як саме це відбувається в окремих випадках.

Логічна форма

Як ми говорили на початку нашого дослідження дедуктивної логіки, є три речі, які повинна робити така логіка: (1) приручити природну мову; (2) точно визначити логічну форму; і (3) розробити спосіб перевірки логічних форм на валідність. До цих пір ми були стурбовані першим кроком. Настав (нарешті) час приступити до другого і третього.

Логічна форма категоричного силогізму визначається двома ознаками аргументу: його настроєм і фігурою. По-перше, настрій. Настрій силогізму визначається типами категоричних суджень, що містяться в аргументі, і порядком, в якому вони відбуваються. Щоб визначити настрій, поставте аргумент в стандартну форму, а потім просто перерахуйте типи категорій (A, E, I, O), ознаками в тому порядку, в якому вони зустрічаються. Давайте зробимо це з нашим дурним прикладом:

Деякі республіканці є гравцями в гольф.
Всі бурундуки - республіканці.
Тому деякі бурундуки є гравцями в гольф.

Зверху вниз у нас є I, A, і I. Таким чином, настрій нашого аргументу IAI. Це так просто. Виявляється, існує 64 можливих настрою - 64 способи об'єднання A, E, I і O в унікальні трилітерні комбінації, від ААА до OOO і все, що між ними.

Іншим аспектом логічної форми є фігура аргументу. Фігура категоричного силогізму визначається розташуванням його термінів. Враховуючи обмеження нашого визначення, існує чотири різні можливості для силогізмів стандартної форми. Ми перерахуємо їх схематично, використовуючи ці конвенції: нехай 'S' позначає другорядний термін, 'P' означає основний термін, а 'M' - для середньострокової. Ось чотири цифри:

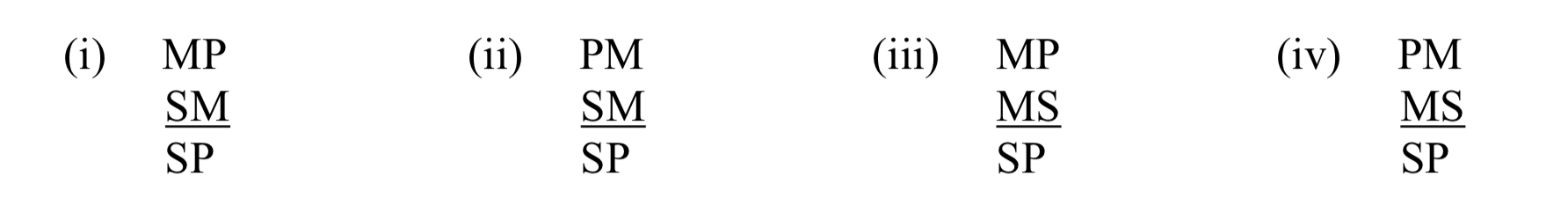
Знову ж таки, єдине, що визначає цифру, - це розташування термінів - чи з'являються вони в предметному або присудковому положенні у своїх приміщеннях. У наших схемах, що буква вказана першою вказує на те, що термін з'являється в позиції суб'єкта; що він з'являється другим вказує на те, що він знаходиться в положенні присудка. Отже, на першому малюнку, у головній передумові (першому), середній член (M) знаходиться в предметній позиції, а основний термін (P) - у позиції присудка. Зверніть увагу, що для всіх чотирьох цифр суб'єкт і присудок висновку залишаються однаковими: це відбувається тому, що за визначенням другорядний термін (S) є предметом висновку і основним терміном (П) його присудком.

Повертаючись до нашого дурного прикладу, можна визначити його фігуру:

Деякі республіканці є гравцями в гольф.
Всі бурундуки - республіканці.
Тому деякі бурундуки є гравцями в гольф.

Мабуть, найпростіше зробити це зосередитися на середньостроковій перспективі, той, який з'являється в кожному з приміщень - в даному випадку «республіканці». Це відбувається в предметному положенні в головній передумові, потім в позиції предиката в другорядній передумові. Скануючи чотири фігури, я просто шукаю ту, яка має 'M' перераховані в першій позиції вгорі, потім другу позицію посередині. Це перша цифра.

Таким чином, настрій нашого зразка аргументу IAI, і це на першій цифрі. Логічна форма - це якраз настрій і фігура, і умовно перерахуємо логічні форми так: ІАІ-1 (настрій, тире, потім число від 1 до 4 для фігури).

Є 4 фігури і 64 настрою. Це дає нам 256 можливих логічних форм. Виявляється, дійсні лише 15 з них. Нам потрібен спосіб перевірити їх. Саме до цього завдання ми зараз перейдемо.

Тест діаграми Венна на валідність

Щоб перевірити силогістичні форми на валідність, ми діємо в три етапи:

1. Намалюйте три кола, що перекриваються, ось так:

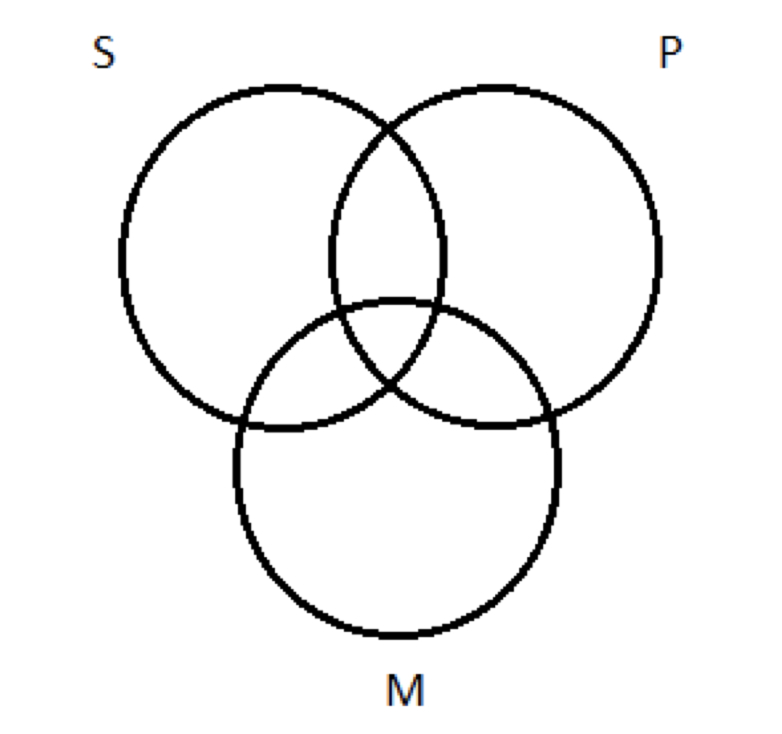
Це дає нам одне коло для кожного з трьох термінів у силогізмі: мінор (S), мажор (P) та середній (M).

2. Зобразіть твердження, зроблені передумовами силогізму на цій діаграмі, використовуючи затінення та Xs відповідно, зображуючи окремі пропозиції A, E, I або O звичайним чином:

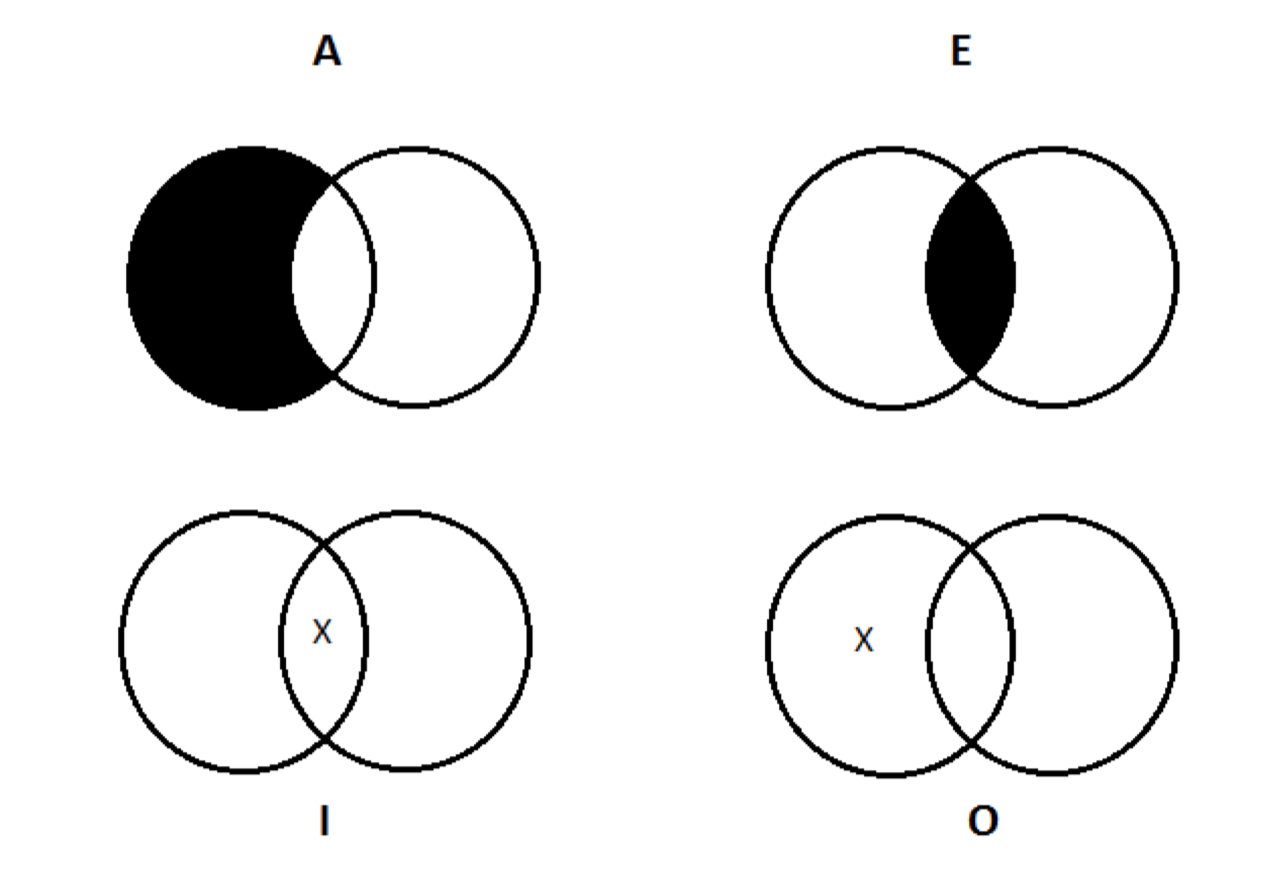
Кожне з приміщень буде пропозицією, що стосується лише двох з трьох класів (S, P та M). Основна передумова стосуватиметься M і P (в деякому порядку); незначна передумова стосуватиметься M і S (в деякому порядку). Те, як будуть маркуватися кола (з S, M, P) буде залежати від цих деталей.

3. Після того як приміщення було зображено на триколірній схемі, дивимося готовий виріб і запитуємо: «Чи тягне за собою ця картина правдивість висновку?» Якщо це так, форма є дійсною; якщо вона не є, вона недійсна.

Під час виконання тесту ми будемо мати на увазі дві речі - одне правило і одна конвенція:

Емпіричне правило: На кроці 2 зобразіть універсальні (A та E) приміщення перед конкретними (I та O) (якщо є вибір).

Умовність: У випадках невизначеності намалюйте Xs трансмісійні лінії кордону.

Нам потрібно пояснити, що означає «невизначеність»; ми будемо через мить. Наразі, щоб все це було зрозуміліше, нам слід пробігти кілька прикладів.

Почнемо з початку (алфавітно-чисельно): AAA-1. Ми хочемо перевірити цю силогістичну форму на валідність. Як виглядає аргумент цієї форми, схематично? Ну, всі три його пропозиції є універсальними стверджуючими, тому всі вони мають форму Всі __ є __. У нас є:

Всі __ є __
Всі __ є __
Отже, всі __ є __

Ось що нам говорить настрій (AAA). Ми повинні з'ясувати, як заповнити пробіли з S, P і M. Цифра говорить нам, як це зробити. ААА-1: Отже, перша цифра. Це виглядає так:

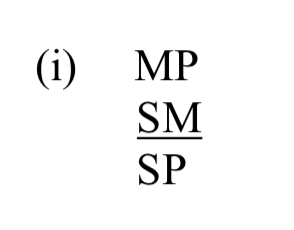
Отже, ААА-1 можна схематично винести таким чином:

Всі М є P.
Всі S є М.
Таким чином, всі S є P.

Щоб перевірити цю форму на валідність, починаємо з кроку 1, і малюємо три кола:

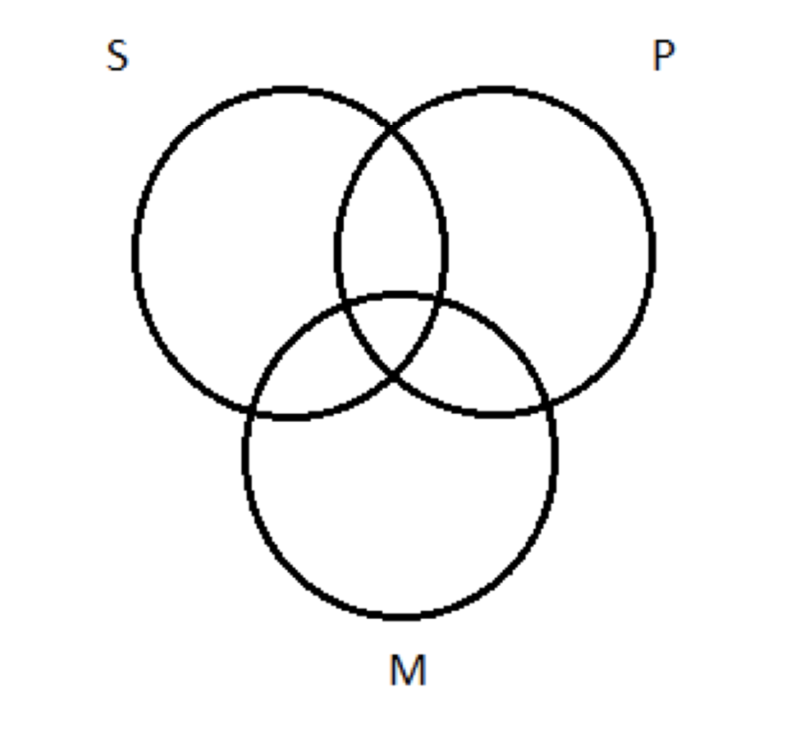
На кроці 2 ми зображуємо приміщення на цій схемі. (Ми повинні мати на увазі правило, що, враховуючи вибір, ми повинні зображати універсальні приміщення перед конкретними, але оскільки обидва приміщення є універсальними, це правило не поширюється на цей випадок.) Ми можемо почати з основної передумови: всі М є P. На регулярній двоколірній діаграмі Венна, що виглядатиме так:

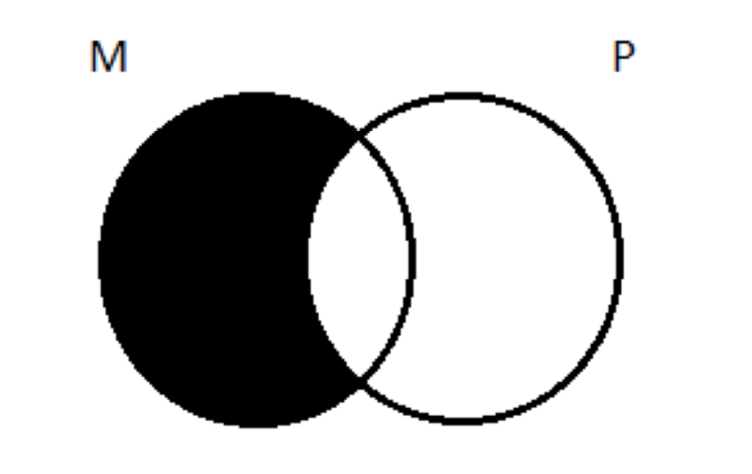
Хитрість полягає в тому, щоб перенести цю діаграму з двома кругами на три кола. При цьому ми маємо на увазі, що всі частини M, які знаходяться поза P, повинні бути затінені. Це дає нам це:

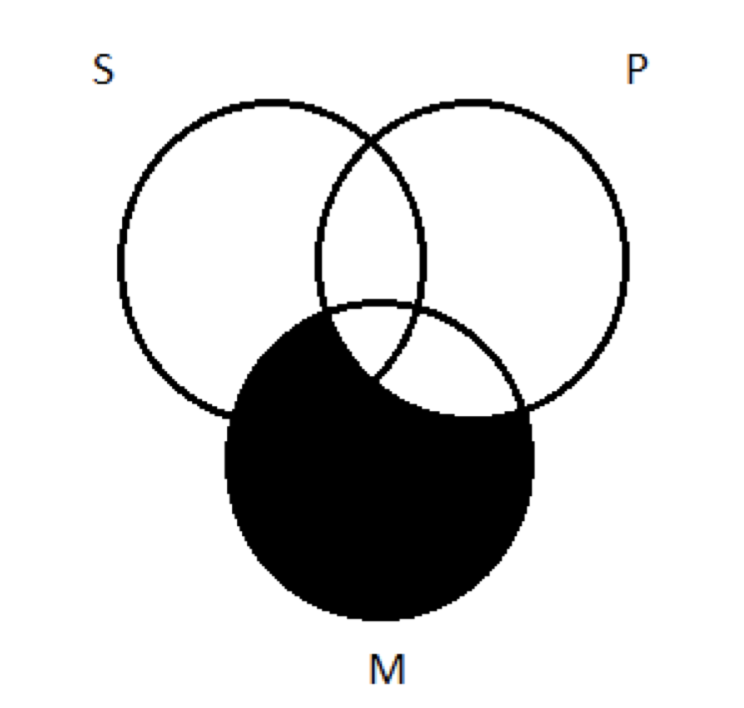
Зверніть увагу, що в ході затінення потрібних областей М ми затінювали частину S. Це нормально. Ті члени класу S - це Ms, які не є Ps; немає такої речі, тому вони повинні йти.

Далі зображуємо другорядну передумову: Всі S - це М. З двома колами, що б виглядало так:

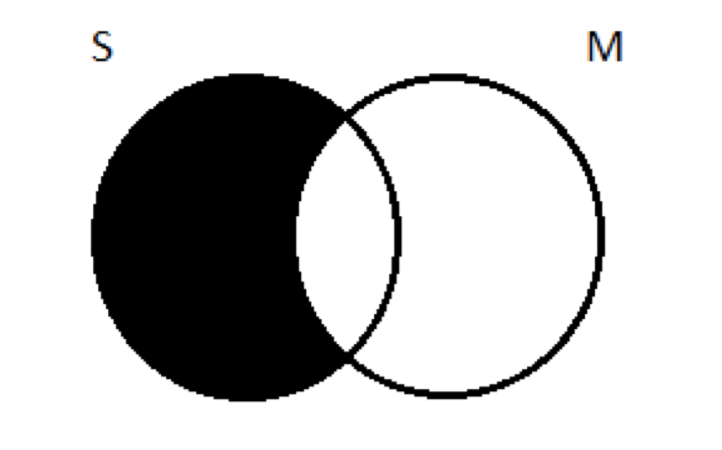
Перенесення цього на діаграму трьох кіл означає затінення всіх частин S поза M:

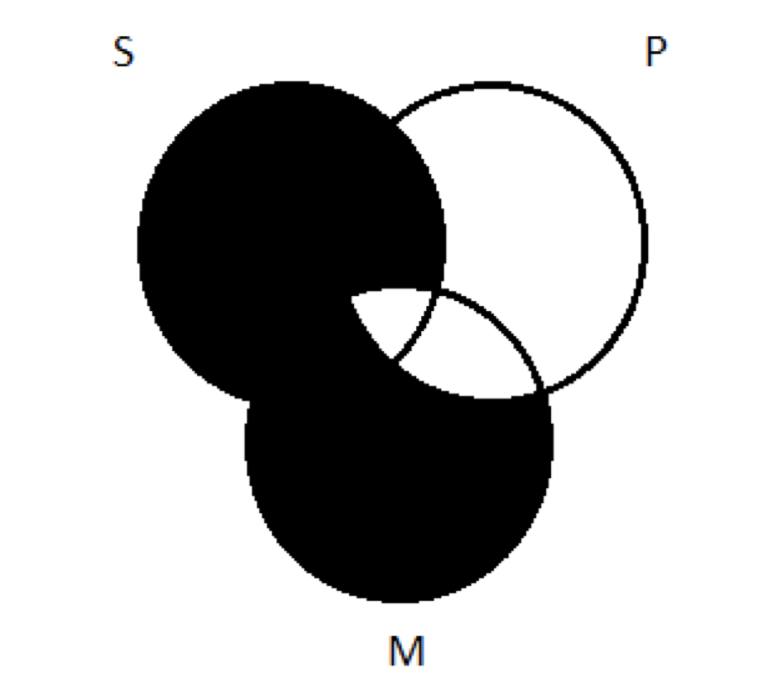
Крок 2 завершений: ми зобразили твердження, зроблені приміщенням. На кроці 3 ми запитуємо, чи гарантує ця діаграма істинність висновку. Ну, наш висновок - все S є P. У діаграмі з двома кругами, що виглядає так:

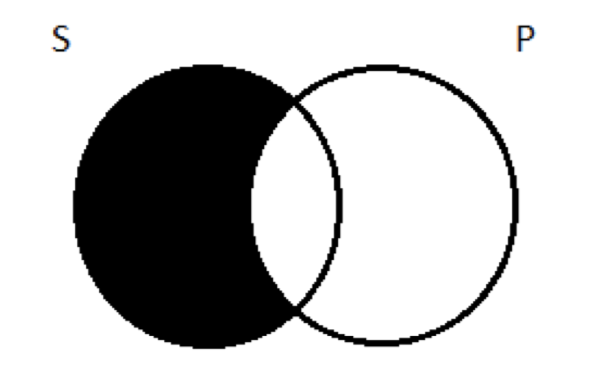
Чи гарантує наша триколірна діаграма правду All S є P? Зосереджуючись на S і P колах і порівнюючи дві діаграми, є невелика різниця: частина області перекриття між S і P затінена в нашій триколірній діаграмі, але це не в зображенні двох кіл. Але це не впливає на наше судження про те, чи гарантує діаграма Всі S є P. Пам'ятайте, це можна розглядати як твердження про те, що певної речі не існує - S, що знаходиться за межами кола P. Якщо є якісь Ss (а їх може і не бути), вони теж будуть Ps. Наша триколірна діаграма насправді гарантує це. Там не може бути S, що не P; ці області затінені. Будь-який S, який ви знайдете, також буде P; це буде в тій маленькій області в центрі, де всі три кола перекриваються.

Отже, оскільки відповідь на наше питання - «так», силогістична форма ААА-1 діє. Тривіальний факт: всім дійсним силогістичним формам в середні віки давали мнемонічні прізвиська, щоб допомогти учням запам'ятати їх. ААА-1 називається «Варвара». Ні насправді. Всі літери в назві мали певне значення: голосні вказують на настрій (AAA); інші літери означають особливості форми, які виходять за рамки нашого короткого дослідження Аристотелівської логіки.

Ми повинні на мить задуматися над тим, чому цей метод працює. Малюємо картину, на якій зображені твердження, зроблені передумовами аргументу. Тоді ми запитуємо, чи гарантує ця картина висновок. Це повинно звучати звично. Ми тестуємо на валідність, і за визначенням аргумент є дійсним на випадок, якщо його приміщення гарантують його висновок; тобто, ЯКЩО приміщення вірні, то висновок також повинен бути вірним. Наш метод відображає визначення. Коли ми зображуємо приміщення на триколірній схемі, ми малюємо картину того, як воно виглядає, щоб приміщення було правдою. Тоді ми запитуємо про цю картину, яка показує світ, в якому передумови правдиві - чи змушує це нас прийняти висновок - чи зображує вона світ, в якому висновок повинен бути правдивим. Якщо це так, аргумент є дійсним; якщо це не так, то це не так. Метод випливає безпосередньо з визначення дійсності.

Щоб додатково проілюструвати метод, слід зробити ще кілька прикладів. AII-3 є корисним. Настрій говорить нам, що це буде виглядати так:

Всі __ є __
Деякі __ є __
Тому деякі __ є __

І ми на третьому малюнку:

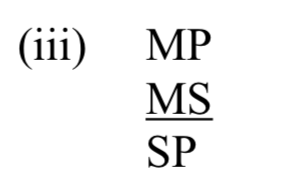
Так заповнюємо заготовки, щоб отримати схематичну форму:

Всі M є P
Деякі M є S
Тому деякі S є P

Починаємо перевірку цієї форми з заготовки триколірної схеми:

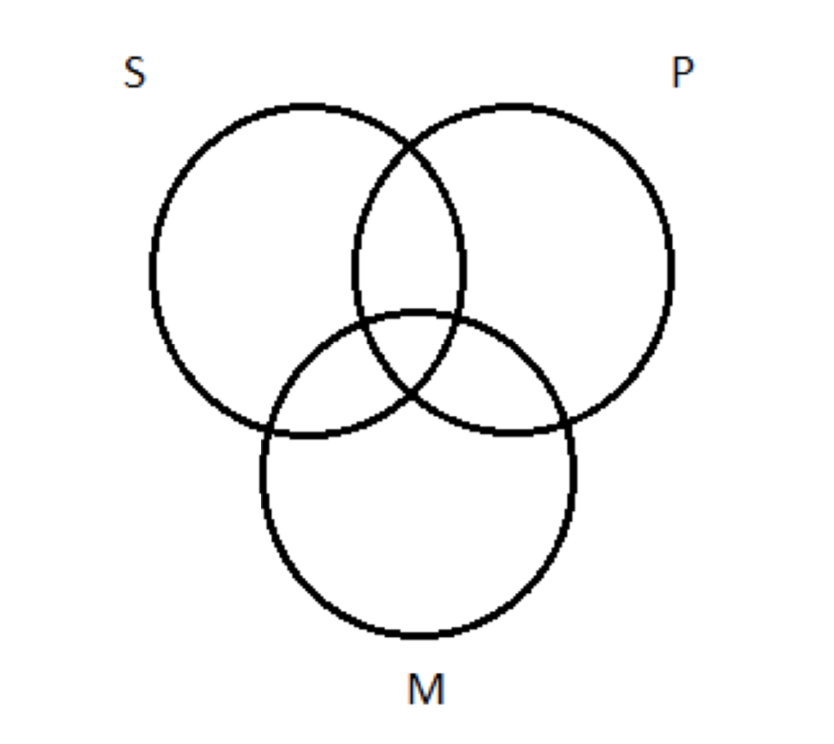
Крок 2: зображуємо приміщення. І тут діє наше емпіричне правило: зобразити універсали перед деталями. Основна передумова - універсальна (А) пропозиція; незначна передумова - це особлива (I). Тому ми зображуємо основну передумову в першу чергу. Ось і все М є П. Ми це вже зробили. Нагадаємо, що Барбара має таку ж основну передумову. Отже, зображення, що на схемі дає нам це:

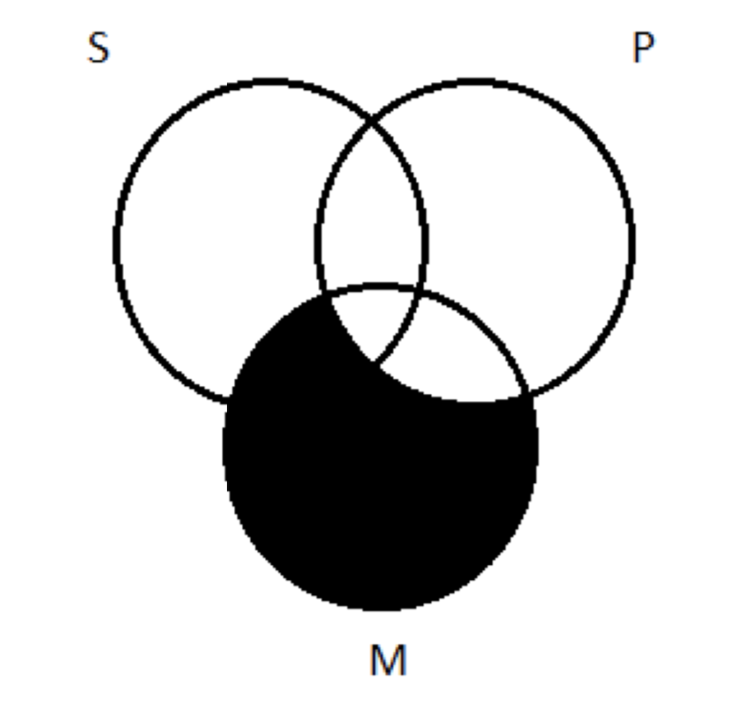
Далі незначна передумова: Деякі M є S. нагадаємо, з конкретними пропозиціями, ми зображуємо їх за допомогою X, щоб вказати річ, яка говорила, що існує. Ця пропозиція стверджує, що є принаймні одна річ, яка є і M, і S:

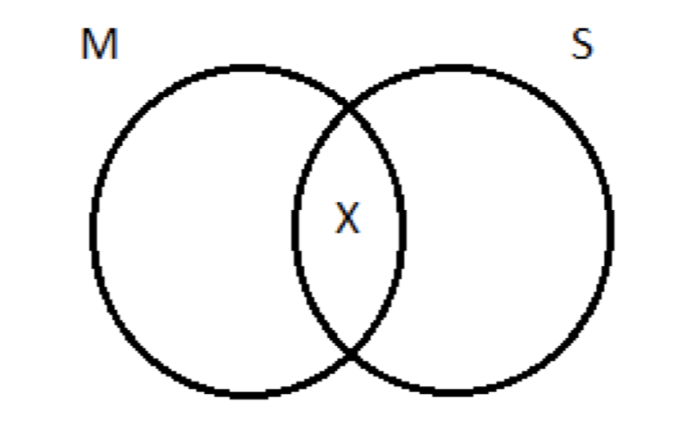
Нам потрібно перенести це на триколірну схему. Нам потрібен X, який знаходиться в обох M і S колах. Якщо ми подивимося на область перекриття між двома, ми бачимо, що частина його була затінена в результаті зображення основної передумови, так що є тільки одне місце для X йти:

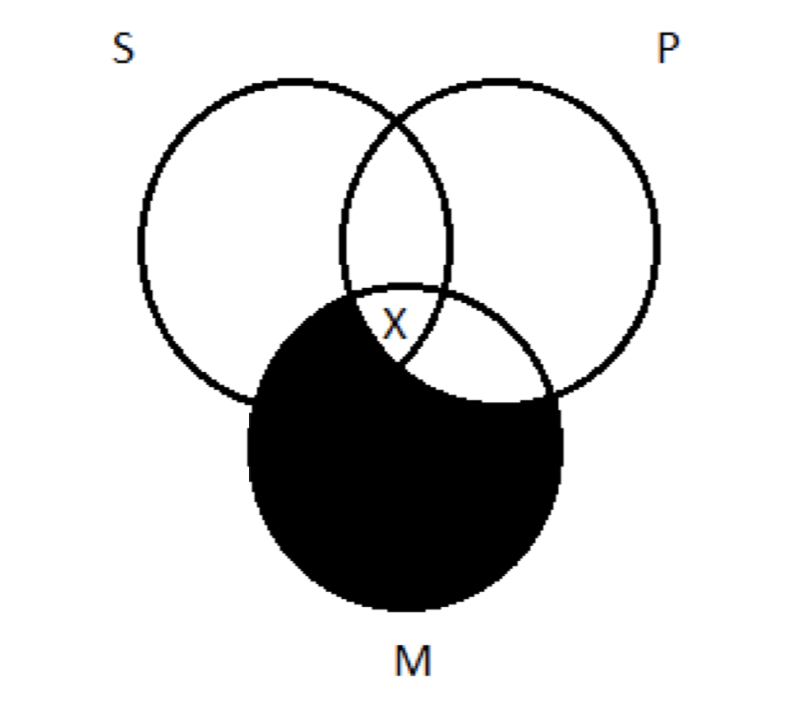
Крок 2 завершений: зображено приміщення. Отже, ми переходимо до кроку 3 і запитуємо: «Чи гарантує ця картина висновок?» Висновок полягає в тому, що деякі S є P; це твердження, що є принаймні одна річ, яка є і S, і P. Чи є? Так! Той Х, який ми намалювали в ході зображення другорядної передумови, знаходиться в солодкому місці - область перекриття між S і P. Це гарантує висновок. Аргумент є справедливим. (Якщо вам цікаво, його мнемонічне прізвисько - «Datisi». Дивно, я знаю; це було Середньовіччя.)

Це ще одне успішне використання тесту на діаграму Венна для валідності, але я хочу повернутися до деяких з них. Я хочу, щоб ми розмірковували над тим, чому у нас є правило зображати універсальні приміщення перед конкретними. Пам'ятайте, що у нас була універсальна основна передумова Всі М є P і конкретна незначна передумова Деякі М є S. Емпіричне правило змусило нас зобразити їх у такому порядку. Чому? Що б сталося, якби ми зробили речі навпаки? Ми б почали з порожньої діаграми три кола і повинні були зобразити деякі M є S на ній. Це означає, що X в області перекриття між M і S. Ця область, однак, розділена на два субрегіони (позначені 'a' і 'b'):

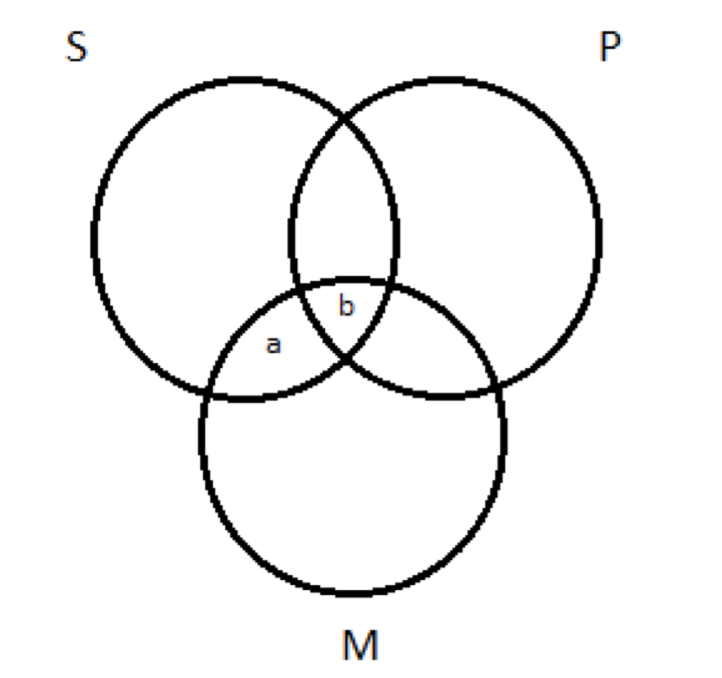
Де я можу поставити свій X - в області a або b? Зверніть увагу, це робить різницю: якщо я поклав X є область a, то це поза P коло; якщо я поклав його в область b, то це всередині P коло. Питання: «Це річ, про яку говорить незначна передумова, існує P чи ні P?» Я зображую передумову, яка лише стверджує, що деякі М є S. Ця передумова нічого не говорить про П. Це мовчить на наше запитання; це не дає нам вказівок щодо вибору між регіонами a та b Що робити? Це один із випадків «невизначеності», про який ми згадували раніше, коли ми ввели конвенцію, яку слід пам'ятати при запуску тесту на валідність: У випадках невизначеності намалюйте Xs трансмісійні лінії кордону. У нас немає жодного способу вибору між регіонами a та b, тому, коли ми малюємо наш X, ми розділимо різницю:

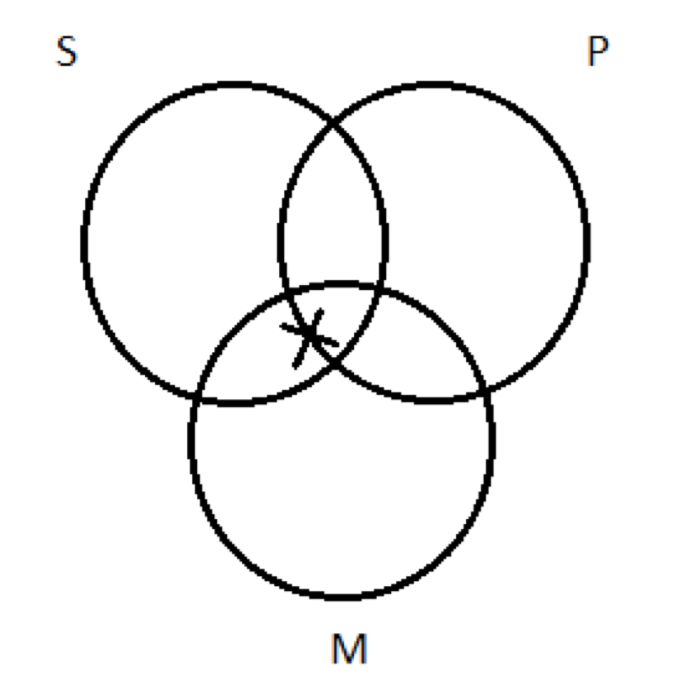
Цей малюнок вказує на те, що є X там десь, або всередині або за межами P коло, ми не знаємо, який.

І тепер ми бачимо причину нашого правила великого пальця - зображуємо універсали перед деталями. Тому що, якщо ми перейдемо до зображення універсальної передумови All M є P, ми відтіняємо таким чином:

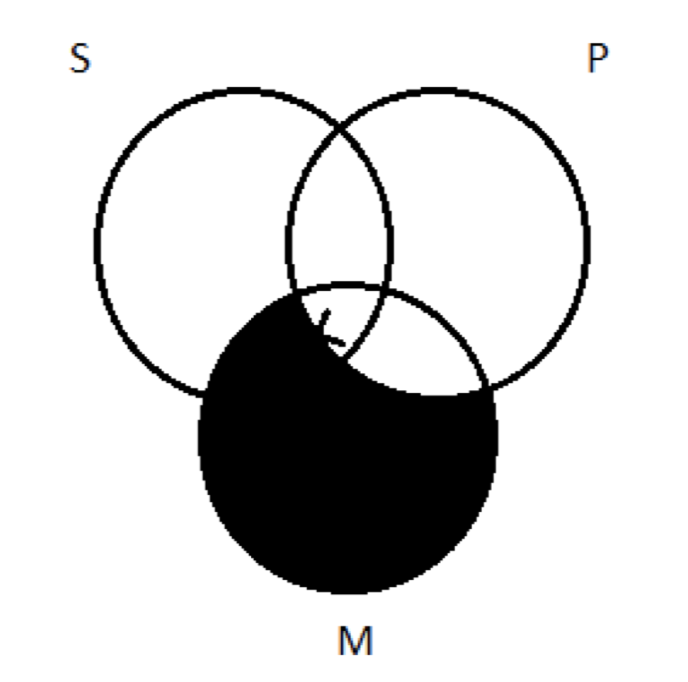
Затінення стерло половину нашого X. Тобто вирішило наше питання про те, чи повинен X йти в окружності P: він повинен. Отже, тепер ми повинні повернутися назад стерти половину AN-X, що залишилося, і повторно намалювати X в цій центральній області і в кінцевому підсумку з готовою діаграмою ми приїхали раніше:

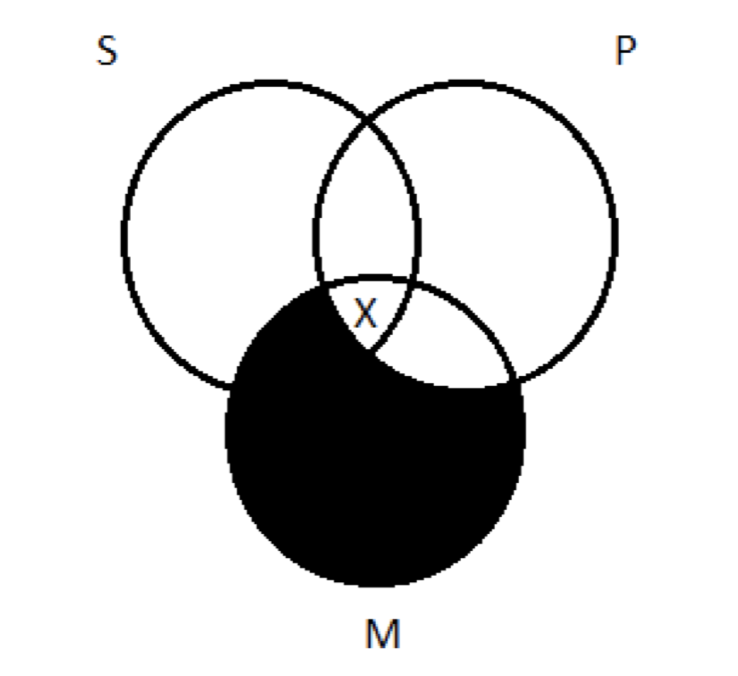
Ми врятували б собі неприємності, якби ми просто дотримувалися правила, щоб почати з і зобразили універсал перед особливим - затінення перед X. Це корисність правила: іноді це усуває невизначеність, яка інакше була б присутня.

Ще один приклад, щоб проілюструвати, як працює цей метод. Давайте перевіримо EOI-1. Відзначивши, що на першому малюнку середнім терміном є спочатку підмет, а потім присудок, ми можемо швидко заповнити схему:

Ні М є P
Деякі S не M
Тому деякі S є P.

Слідуючи правилу, спочатку зображуємо універсальну (E) передумову. Ні M є P стверджує, що немає нічого, що є в обох цих класах. Площа перекриття між ними порожня. З двома колами ми маємо це:

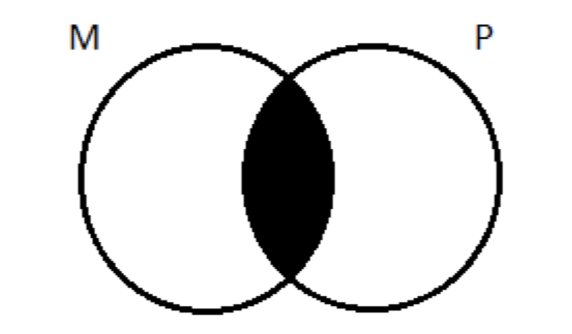
Перенесівши це на триколірну діаграму, затінюємо всю площу перекриття між M і P колами (відсікаючи по шляху частина S):

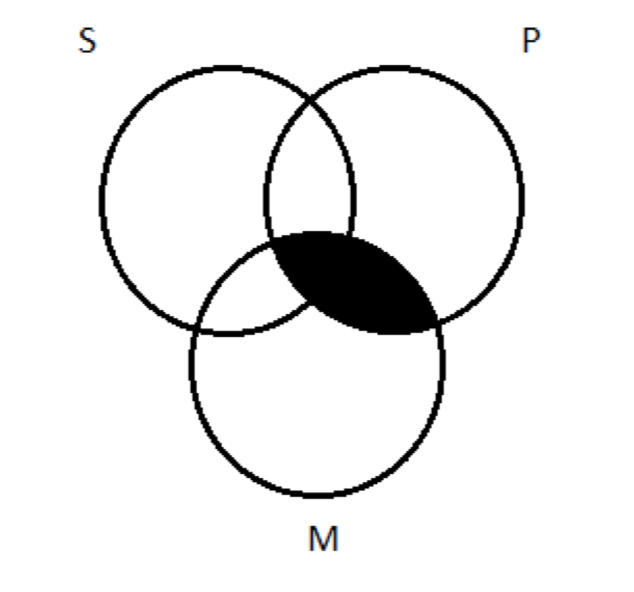
Далі, особлива (O) передумова: Деякі S не є М. Це стверджує існування something— а саме, річ, яка є S, але не М. Нам потрібен X у колі S, що поза M кола:

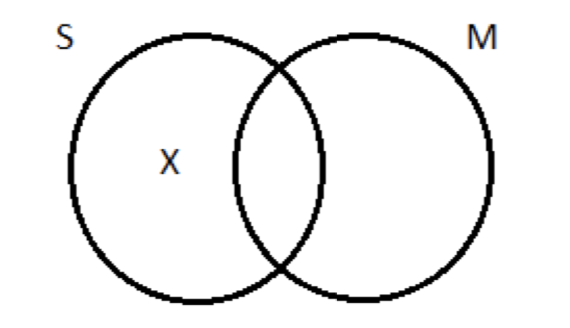
Однак, переходячи до діаграми з трьома колами, все стає брудним. Площа S, що знаходиться за межами M, ділиться на два субрегіони (позначені 'a' і 'b'):

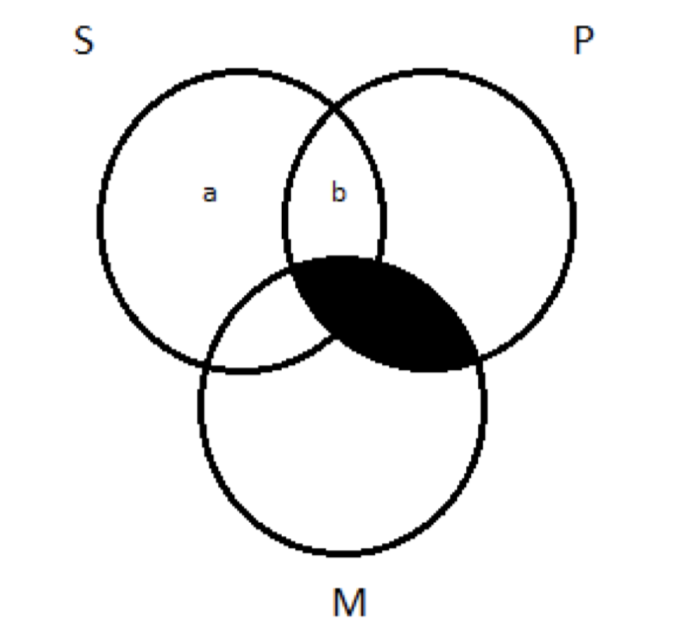
Нам потрібен X десь там, але ми ставимо його в область а або регіон b? Це має значення: якщо ми поставимо його в область b, це P; якщо ми поставимо його в область a, це не так. Це та сама проблема, з якою ми стикалися раніше. Ми зображуємо приміщення - деякі S не M - це мовчить на питання про те, чи є річ невизначеністю P. Ми не можемо визначитися між a та b, тому ми розділимо різницю:

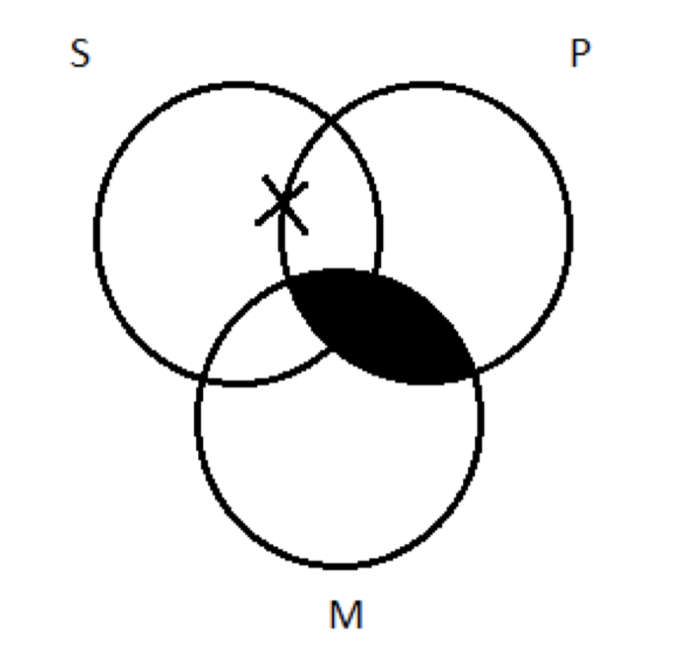
Що X може бути всередині P, а може і ні; ми не знаємо. Це випадок, коли ми дотримувалися правила, зображуючи універсальну передумову перед конкретною, але вона не мала тієї користі, яку вона мала, коли ми тестували AII-3: це не видалило невизначеності. Це може статися. Емпіричне правило діє, оскільки воно іноді усуває невизначеність; хоча це не завжди працює.

Тож тепер, коли ми зобразили приміщення, ми запитуємо, чи гарантують вони висновок. Чи є світ, зображений на нашій діаграмі, той, в якому висновок повинен бути вірним? Висновок полягає в тому, що деякі S є P: він стверджує, що є принаймні одна річ, яка є і S, і P. Чи є наша картина така річ? На малюнку є X. Чи підходить він під рахунок? Це і S, і P? Ну, ех... Може бути? Що X може бути всередині області перекриття між S і P; знову ж таки, це може бути не так.

Ой. Що ми говоримо? Спокусливо сказати це: ми не знаємо, чи є аргумент дійсним чи ні; це залежить від того, де насправді знаходиться цей Х. Але це не правильна відповідь. Пам'ятайте, що ми тестуємо на валідність - чи гарантують приміщення висновок. Ми можемо відповісти на це питання: вони цього не роблять. Для гарантії нам знадобиться X на нашій картині, яка, безумовно, знаходиться всередині цього середнього регіону. У нас немає такого X. Ці приміщення залишають відкритою можливість того, що висновок вірний; вони цього не виключають. Але цього недостатньо для обґрунтованості. Щоб аргумент був дійсним, приміщення повинно вимагати укладення, змусити його на нас. Це не так. Форма EOI-1 недійсна. (Сумно, але правда: недійсні силогістичні форми не мають мнемонічних прізвиськ.)

Вправи

1. Визначте логічну форму наступних аргументів.

(а) Оскільки деякі вісконсиніти є злочинцями, а всі злочинці - негідники, з цього випливає, що деякі негідники є вісконсинітами.
(б) Жодні серфери не є священиками, тому що всі священики - чоловіки, а деякі серфери - не чоловіки.
(c) Деякі автори є феміністками, оскільки деякі жінки є авторами, а деякі жінки - феміністки.
(г) Всі комарі є потенційними переносниками хвороб; тому деякі комарі становлять загрозу суспільству, оскільки всі потенційні переносники хвороб становлять загрозу суспільству.
(e) Оскільки деякі неонацисти є блогерами, деякі неонацисти не є геніями, оскільки жоден геній не є блогерами.

2. Перевірте наступні силогістичні форми на валідність.

a) ЕАЕ-2
(b) ЕАЕ-3
(c) ОАО-3
(d) ЕІО-4
(е) АОО-4
(f) ІАІ-1
(g) АІІ-1

3. Перевірте наступні аргументи на достовірність.

(а) Деякі пірати є найманцями; отже, деякі моряки є піратами, тому що всі моряки є найманцями.
(б) Деякі жінки не черниці, але всі черниці - кохані; з цього випливає, що деякі жінки не є коханими.
(c) Деякі республіканці не є політиками, бо деякі республіканці не є християнами, а деякі християни не є політиками.

4. Перевірте аргументи у вправі 1 на достовірність.