9.11: Охоронність

Last updated
Save as PDF

Page ID: 52889

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Система деривації, така як природний дедукція, є здоровою, якщо вона не може вивести речі, які насправді не слідують. Таким чином, надійність є своєрідним гарантованим властивістю безпеки для систем деривації. Залежно від того, про яку теоретичну властивість доказу йде мова, ми хотіли б знати, наприклад, що

кожне похідне речення є дійсним;
якщо вирок випливає з деяких інших, то воно також є їх наслідком;
якщо сукупність пропозицій суперечлива, вона незадовільна.

Це важливі властивості дериваційної системи. Якщо хтось із них не тримається, система деривації є недостатньою - вона призведе до занадто багато. Отже, встановлення надійності системи деривації має першорядне значення.

Теорема\(\PageIndex{1}\): Soundness

Якщо\(A\) виводиться з нерозряджених припущень\(\Gamma\), то\(\Gamma \Entails A\).

Доказ. \(\delta\)Дозволяти бути виведенням\(A\). Приступаємо по індукції за кількістю умовиводів в\(\delta\).

Для індукційної основи показуємо претензію, якщо кількість умовиводів дорівнює\(0\). В даному випадку\(\delta\) складається тільки з єдиного речення\(A\), тобто припущення. Це припущення є нерозрядженим, оскільки припущення можуть бути виписані лише умовиводами, а висновків немає. Отже, будь-яка структура,\(\Struct{M}\) яка задовольняє всім нерозрядженим припущенням доказу, також задовольняє\(A\).

Тепер про індуктивному кроці. Припустимо, що\(\delta\) містить\(n\) висновки. Передумова (и) самого нижнього висновку походять з використанням піддеривацій, кожне з яких містить менше, ніж\(n\) умовиводів. Ми припускаємо індукційну гіпотезу: Передумови самого нижнього висновку випливають з нерозряджених припущень про суб-похідні, що закінчуються в цих приміщеннях. Ми повинні показати, що висновок\(A\) випливає з нерозряджених припущень всього доказу.

Розрізняємо відмінки за типом самого нижнього висновку. Спочатку розглянемо можливі висновки тільки з однією передумовою.

Припустимо, що останній висновок\(\Intro{\lnot}\): деривація має вигляд

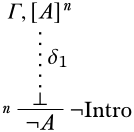
За індуктивною гіпотезою,\(\lfalse\) випливає з нерозряджених\(\Gamma \cup \{A\}\) припущень\(\delta_1\). Розглянемо структуру\(\Struct{M}\). Ми повинні показати, що, якщо\(\Sat{M}{\Gamma}\), то\(\Sat{M}{\lnot A}\). Припустимо, для скорочення що\(\Sat{M}{\Gamma}\), але\(\SatN{M}{\lnot A}\), т. Е\(\Sat{M}{A}\). Це означало б, що\(\Sat{M}{\Gamma \cup \{A\}}\). Це суперечить нашій індуктивній гіпотезі. Отже,\(\Sat{M}{\lnot A}\).
Останній висновок\(\Elim{\land}\): Є два варіанти:\(A\) або\(B\) може бути виведений з передумови\(A \land B\). Розглянемо перший випадок. Виведення\(\delta\) виглядає наступним чином:

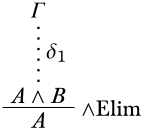
За індуктивною гіпотезою,\(A \land B\) випливає з нерозряджених\(\Gamma\) припущень\(\delta_1\). Розглянемо структуру\(\Struct{M}\). Ми повинні показати, що, якщо\(\Sat{M}{\Gamma}\), то\(\Sat{M}{A}\). Припустимо\(\Sat{M}{\Gamma}\). За нашою індуктивною гіпотезою (\(\Gamma \Entails A \land B\)) ми це знаємо\(\Sat{M}{A \land B}\). За визначенням,\(\Sat{M}{A \land B}\) якщо\(\Sat{M}{A}\) і\(\Sat{M}{B}\). (Випадок, з якого\(B\) виводиться\(A \land B\), обробляється аналогічно.)
Останній висновок\(\Intro{\lor}\): Є два варіанти:\(A \lor B\) може бути виведений з приміщення\(A\) або приміщення\(B\). Розглянемо перший випадок. Похідний має вигляд

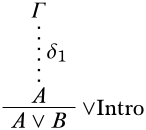
За індуктивною гіпотезою,\(A\) випливає з нерозряджених\(\Gamma\) припущень\(\delta_1\). Розглянемо структуру\(\Struct{M}\). Ми повинні показати, що, якщо\(\Sat{M}{\Gamma}\), то\(\Sat{M}{A \lor B}\). Припустимо\(\Sat{M}{\Gamma}\); то\(\Sat{M}{A}\) з тих пір\(\Gamma \Entails A\) (індуктивна гіпотеза). Так що це також повинно бути так\(\Sat{M}{A \lor B}\). (Випадок, з якого\(A \lor B\) виводиться\(B\), обробляється аналогічно.)
Останній висновок\(\Intro{\lif}\):\(A \lif B\) виводиться з піддоказу з припущенням\(A\) і висновком\(B\), тобто,

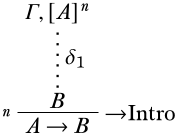
За індуктивною гіпотезою,\(B\) випливає з нерозряджених припущень\(\delta_1\), т. Е\(\Gamma \cup \{A\} \Entails B\). Розглянемо структуру\(\Struct{M}\). Нерозряджені припущення\(\delta\) справедливі\(\Gamma\), так як\(A\) розряджається на останньому висновку. Тому нам потрібно показати, що\(\Gamma \Entails A \lif B\). Для reductio, припустимо, що для якоїсь структури\(\Struct{M}\),\(\Sat{M}{\Gamma}\) але\(\SatN{M}{A \lif B}\). Отже,\(\Sat{M}{A}\) і\(\SatN{M}{B}\). Але за гіпотезою,\(B\) є наслідком\(\Gamma \cup \{A\}\), тобто\(\Sat{M}{B}\), що є протиріччям. Отже,\(\Gamma \Entails A \lif B\).
Останній висновок\(\FalseInt\): Тут\(\delta\) закінчується

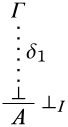
За індукційною гіпотезою,\(\Gamma \Entails \lfalse\). Ми мусимо це показати\(\Gamma \Entails A\). Припустимо, ні; тоді для деяких у\({\Struct{M}}\) нас є\(\Sat{M}{\Gamma}\) і\(\SatN{M}{A}\). Але у нас завжди є\(\SatN{M}{\lfalse}\), так що це означало б\(\Gamma \EntailsN \lfalse\), що, всупереч індукційній гіпотезі.
Останній висновок\(\FalseCl\): Вправа.
Останній висновок\(\Intro{\lforall{}{}}\): Тоді\(\delta\) має форму

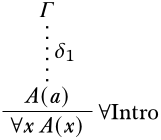
Передумова\(A(a)\) є наслідком нерозряджених припущень\(\Gamma\) індукційної гіпотезою. Розглянемо якусь структуру\(\Struct{M}\), таку, що\(\Sat{M}{\Gamma}\). Нам потрібно це показати\(\Sat{M}{\lforall{x}{A(x)}}\). Оскільки\(\lforall{x}{A(x)}\) це речення, це означає, що ми повинні показати, що для кожного присвоєння змінної\(s\),\(\Sat[,s]{M}{A(x)}\) (Пропозиція 5.12.4). Оскільки\(\Gamma\) складається повністю з речень,\(\Sat[,s]{M}{B}\) для всіх\(B \in \Gamma\) за визначенням 5.11.4. Нехай\(\Struct{M'}\) буде як\(\Struct{M}\) хіба що\(\Assign{a}{M'} = s(x)\). Оскільки\(a\) не відбувається в\(\Gamma\),\(\Sat{M'}{\Gamma}\) Слідство 5.13.1. З тих пір\(\Gamma \Entails A(a)\),\(\Sat{M'}{A(a)}\). Оскільки\(A(a)\) є реченням,\(\Sat[,s]{M'}{A(a)}\) за пропозицією 5.12.3. \(\Sat[,s]{M'}{A(x)}\)iff\(\Sat{M'}{A(a)}\) за пропозицією 5.13.3 (нагадаємо, що\(A(a)\) це просто\(\Subst{A(x)}{a}{x}\)). Отже,\(\Sat[,s]{M'}{A(x)}\). Оскільки\(a\) не відбувається в\(A(x)\), за пропозицією 5.13.1,\(\Sat[,s]{M}{A(x)}\). Але\(s\) була довільна змінна присвоєння, так що\(\Sat{M}{\lforall{x}{A(x)}}\).
Останній висновок\(\Intro{\lexists{}{}}\): Вправа.
Останній висновок\(\Elim{\forall}\): Вправа.

Тепер розглянемо можливі висновки з декількома приміщеннями:\(\Elim{\lor}\),\(\Intro{\land}\),\(\Elim{\lif}\), and \(\Elim{\lexists{}{}}\).

Останній висновок -\(\Intro{\land}\). \(A \land B\)виводиться з приміщення\(A\)\(B\) і\(\delta\) має вигляд

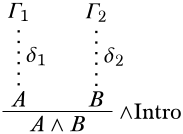
За індукційною гіпотезою,\(A\) випливає з\(\Gamma_1\) нерозряджених припущень\(\delta_1\) і\(B\) випливає з\(\Gamma_2\) нерозряджених припущень\(\delta_2\). Нерозряджені припущення\(\delta\) є\(\Gamma_1 \cup \Gamma_2\), тому ми повинні показати це\(\Gamma_1 \cup \Gamma_2 \Entails A \land B\). Розглянемо структуру\(\Struct{M}\) с\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). Так як\(\Sat{M}{\Gamma_1}\), це повинно бути так, що\(\Sat{M}{A}\) як\(\Gamma_1 \Entails A\), і\(\Sat{M}{B}\) так\(\Sat{M}{\Gamma_2}\), з\(\Gamma_2 \Entails B\). Разом,\(\Sat{M}{A \land B}\).
Останній висновок\(\Elim{\lor}\): Вправа.
Останній висновок -\(\Elim{\lif}\). \(B\)виводиться з приміщення\(A \lif B\) і\(A\). Виведення\(\delta\) виглядає наступним чином:

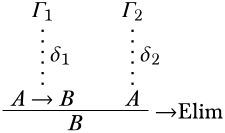
За індукційною гіпотезою,\(A \lif B\) випливає з\(\Gamma_1\) нерозряджених припущень\(\delta_1\) і\(A\) випливає з\(\Gamma_2\) нерозряджених припущень\(\delta_2\). Розглянемо структуру\(\Struct{M}\). Ми повинні показати, що, якщо\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\), то\(\Sat{M}{B}\). Припустимо\(\Sat{M}{\Gamma_1 \cup \Gamma_2}\). З тих пір\(\Gamma_1 \Entails A \lif B\),\(\Sat{M}{A \lif B}\). З тих пір\(\Gamma_2 \Entails A\), у нас є\(\Sat{M}{A}\). Це означає, що\(\Sat{M}{B}\) (Бо якщо\(\SatN{M}{B}\), так як\(\Sat{M}{A}\), ми б мали\(\SatN{M}{A \lif B}\), суперечить\(\Sat{M}{A \lif B}\)).
Останній висновок\(\Elim{\lnot}\): Вправа.
Останній висновок\(\Elim{\lexists{}{}}\): Вправа.

◻

Проблема\(\PageIndex{1}\)

Завершіть доказ теореми\(\PageIndex{1}\).

Слідство\(\PageIndex{1}\)

Якщо\(\Proves A\), то\(A\) дійсний.

Слідство\(\PageIndex{2}\)

Якщо\(\Gamma\) задовольняється, значить, послідовно.

Доказ. Доводимо контрапозитив. Припустимо, що\(\Gamma\) це не послідовно. Потім\(\Gamma \Proves \lfalse\), тобто відбувається виведення\(\lfalse\) з нерозряджених припущень в\(\Gamma\). За теоремою будь-яка структура\(\PageIndex{1}\),\(\Struct{M}\) яка задовольняє,\(\Gamma\) повинна задовольняти\(\lfalse\). Так як\(\SatN{M}{\lfalse}\) для кожної\(\Struct{M}\) споруди ніяка не\(\Struct{M}\) може задовольнити\(\Gamma\),\(\Gamma\) тобто не задовольняє. ◻