Skip to main content
LibreTexts - Ukrayinska

9.8: Вихідність та послідовність

  1. Last updated
  2. Save as PDF
  • Page ID
    52859

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Template:MathJaxZach

    Зараз ми встановимо ряд властивостей відношення похідності. Вони самостійно цікаві, але кожен зіграє свою роль в доведенні теореми про повноту.

    Пропозиція\(\PageIndex{1}\)

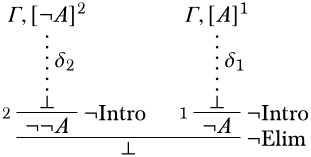
    Якщо\(\Gamma \Proves A\) і\(\Gamma \cup \{A\}\) є непослідовним, то\(\Gamma\) непослідовно.

    Доказ. Нехай виведенням\(A\) від\(\Gamma\) бути\(\delta_1\) і виведенням\(\lfalse\) від\(\Gamma \cup \{A\}\) бути\(\delta_2\). Потім ми можемо вивести:

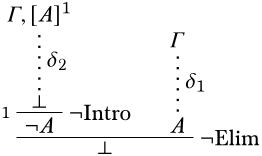
    9.8.1.png

    У новій похідній припущення\(A\) виписується, тому воно є похідним від\(\Gamma\). ◻

    Пропозиція\(\PageIndex{2}\)

    \(\Gamma \Proves A\)iff\(\Gamma \cup \{\lnot A\}\) є непослідовним.

    Доказ. По-перше\(\Gamma \Proves A\), припустимо, тобто є висновок\(A\) з\(\delta_0\) нерозряджених припущень\(\Gamma\). Отримаємо похідний\(\lfalse\) від\(\Gamma \cup \{\lnot A\}\) наступного:

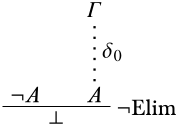
    9.8.2.png

    Тепер припускаємо, що\(\Gamma \cup \{\lnot A\}\) це непослідовно, і нехай\(\delta_1\) буде відповідне виведення\(\lfalse\) з нерозряджених припущень в\(\Gamma \cup \{\lnot A\}\). Ми отримуємо похідний\(A\) від\(\Gamma\) одного за допомогою\(\FalseCl\):

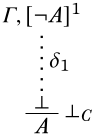
    9.8.3.png

    ◻

    Проблема\(\PageIndex{1}\)

    Доведіть, що\(\Gamma \Proves \lnot A\) iff\(\Gamma \cup \{A\}\) є непослідовним.

    Пропозиція\(\PageIndex{3}\)

    Якщо\(\Gamma \Proves A\) і\(\lnot A \in \Gamma\), то\(\Gamma\) непослідовно.

    Доказ. Припустимо\(\Gamma \Proves A\), і\(\lnot A \in \Gamma\). Потім відбувається виведення\(\delta\)\(A\) від\(\Gamma\). Розглянемо це просте застосування\(\Elim{\lnot}\) правила:

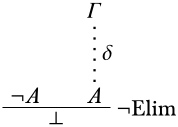
    9.8.4.png

    Оскільки\(\lnot A \in \Gamma\), всі нерозряджені припущення знаходяться в\(\Gamma\), це показує, що\(\Gamma \Proves \lfalse\). ◻

    Пропозиція\(\PageIndex{4}\)

    Якщо\(\Gamma \cup \{A\}\) і\(\Gamma \cup \{\lnot A\}\) обидва несумісні, то\(\Gamma\) непослідовні.

    Доказ. Існують\(\delta_2\) похідні\(\delta_1\) і\(\lfalse\) від\(\Gamma \cup \{ A \}\) і\(\lfalse\) від\(\Gamma \cup \{ \lnot A \}\) відповідно. Потім ми можемо вивести

    9.8.5.png

    Так як припущення\(A\) і\(\lnot A\) виписані, то це виведення\(\lfalse\) від\(\Gamma\) одного. Отже\(\Gamma\), це непослідовно. ◻