8.12: Обґрунтованість

Template:MathJaxZach

Система деривації, така як послідовне обчислення, є звуковою, якщо вона не може вивести речі, які насправді не тримають. Таким чином, надійність є своєрідним гарантованим властивістю безпеки для систем деривації. Залежно від того, про яку теоретичну властивість доказу йде мова, ми хотіли б знати, наприклад, що

1. кожен похідний\(A\) є дійсним;

2. якщо вирок випливає з деяких інших, то воно також є їх наслідком;

3. якщо сукупність пропозицій суперечлива, вона незадовільна.

Це важливі властивості дериваційної системи. Якщо хтось із них не тримається, система деривації є недостатньою - вона призведе до занадто багато. Отже, встановлення надійності системи деривації має першорядне значення.

Оскільки всі ці доказно-теоретичні властивості визначаються через похідність у послідовному обчисленні певних послідовностей, доведення (1) — (3) вище вимагає доведення чогось про семантичні властивості похідних послідовностей. Спочатку ми визначимо, що означає, щоб послідовність була дійсною, а потім покажемо, що кожна похідна послідовність є дійсною. (1) — (3) потім слідують за наслідками цього результату.

Визначення\(\PageIndex{1}\)

Структура\(\Struct M\) задовольняє послідовний\(\Gamma \Sequent \Delta\) iff або\(\SatN{M}{A}\) для деяких,\(A \in \Gamma\) або\(\Sat{M}{A}\) для деяких\(A \in \Delta\).

Послідовність діє, якщо кожна структура її\(\Struct M\) задовольняє.

Теорема\(\PageIndex{1}\): Soundness

Якщо\(\Log{LK}\) виводить\(\Theta \Sequent \Xi\), то\(\Theta \Sequent \Xi\) дійсний.

Доказ. \(\pi\)Дозволяти бути виведенням\(\Theta \Sequent \Xi\). Приступаємо по індукції за кількістю умовиводів\(n\) в\(\pi\).

Якщо кількість умовиводів є\(0\), то\(\pi\) складається тільки з початкової послідовності. Кожна початкова послідовність,\(A \Sequent A\) очевидно, дійсна, оскільки для кожного\(\Struct M\),\(\SatN{M}{A}\) або\(\Sat{M}{A}\).

Якщо кількість умовиводів більше 0, розрізняємо відмінки за типом самого нижнього висновку. За індукційною гіпотезою можна припустити, що передумови цього висновку є дійсними, оскільки кількість висновків у доказі будь-якої передумови менше, ніж\(n\).

Спочатку розглянемо можливі висновки тільки з однією передумовою.

1. Останній висновок - ослаблення. Тоді\(\Theta \Sequent \Xi\) є або\(A, \Gamma \Sequent \Delta\) (якщо останній висновок є\(\LeftR{\Weakening}\)) або\(\Gamma \Sequent \Delta, A\) (якщо це\(\RightR{\Weakening}\)), і деривація закінчується в одному з

   

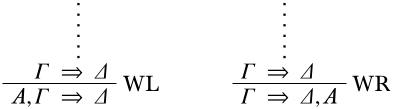
   За індукційною гіпотезою,\(\Gamma \Sequent \Delta\) є дійсним, тобто для кожної структури\(\Struct{M}\), або є якась\(C \in \Gamma\) така, що\(\SatN{M}{C}\) або є якась\(C \in \Delta\) така, що\(\Sat{M}{C}\).

   Якщо\(\SatN{M}{C}\) для деяких\(C \in \Gamma\), то\(C \in \Theta\) як і так\(\Theta = A, \Gamma\), і так\(\SatN{M}{C}\) для деяких\(C \in \Theta\). Аналогічно, якщо\(\Sat{M}{C}\) для деяких\(C \in \Delta\), як\(C \in \Xi\),\(\Sat{M}{C}\) для деяких\(C \in \Xi\). Отже,\(\Theta \Sequent \Xi\) діє.

2. Останній висновок\(\LeftR{\lnot}\): Тоді передумова останнього висновку є,\(\Gamma \Sequent \Delta, A\) і висновок є\(\lnot A, \Gamma \Sequent \Delta\), тобто похідний закінчується

   

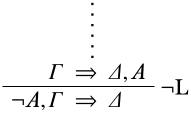
   і\(\Theta = \lnot A, \Gamma\) поки\(\Xi = \Delta\).

   Індукційна гіпотеза говорить нам, що\(\Gamma \Sequent \Delta, A\) дійсна\(\Struct{M}\), тобто для кожного, або (а) для деяких\(C \in \Gamma\)\(\SatN{M}{C}\), або (b) для деяких\(C \in \Delta\)\(\Sat{M}{C}\), або (c)\(\Sat{M}{A}\). Ми хочемо показати, що також\(\Theta \Sequent \Xi\) є дійсним. \(\Struct{M}\)Дозволяти буде будовою. Якщо (а) тримає, то є\(C \in \Gamma\) так\(\SatN{M}{C}\), що, але\(C \in \Theta\) так само. Якщо (б) тримає, є\(C \in \Delta\) таке\(\Sat{M}{C}\), що, але\(C \in \Xi\) також. Нарешті, якщо\(\Sat{M}{A}\), то\(\SatN{M}{\lnot A}\). Так як\(\lnot A \in \Theta\), є\(C \in \Theta\) таке, що\(\SatN{M}{C}\). Отже,\(\Theta \Sequent \Xi\) діє.

3. Останній висновок\(\RightR{\lnot}\): Вправа.

4. Останній висновок\(\LeftR{\land}\): Є два варіанти:\(A \land B\) може бути виведений зліва від\(A\) або з\(B\) лівого боку приміщення. У першому випадку\(\pi\) закінчується в

   

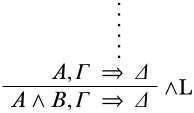
   і\(\Theta = A \land B, \Gamma\) поки\(\Xi = \Delta\). Розглянемо структуру\(\Struct M\). Оскільки за індукційною гіпотезою,\(A, \Gamma \Sequent \Delta\) є дійсним\(\SatN{M}{A}\), (а), (b)\(\SatN{M}{C}\) для деяких\(C \in \Gamma\), або (c)\(\Sat{M}{C}\) для деяких\(C \in \Delta\). У випадку (а)\(\SatN{M}{A \land B}\), так є\(C \in \Theta\) (а саме,\(A \land B\)) такий, що\(\SatN{M}{C}\). У випадку (б), є\(C \in \Gamma\) таке\(\SatN{M}{C}\), що, а\(C \in \Theta\) також. У випадку (с), є\(C \in \Delta\) таке\(\Sat{M}{C}\), що,\(C \in \Xi\) а так само з\(\Xi = \Delta\). Так що в кожному конкретному випадку\(\Struct M\) задовольняє\(A \land B, \Gamma \Sequent \Delta\). Так як\(\Struct{M}\) був\(\Gamma \Sequent \Delta\) довільним, є дійсним. Випадок, з якого\(A \land B\) виводиться,\(B\) обробляється однаково, змінюючи\(A\) на\(B\).

5. Останній висновок\(\RightR{\lor}\): Є два варіанти:\(A \lor B\) може бути виведений праворуч від\(A\) або з правого\(B\) боку приміщення. У першому випадку\(\pi\) закінчується

   

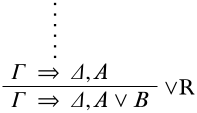
   Тепер\(\Theta = \Gamma\) і\(\Xi = \Delta, A \lor B\). Розглянемо структуру\(\Struct{M}\). Оскільки\(\Gamma \Sequent \Delta, A\) дійсний, (a)\(\Sat{M}{A}\), (b)\(\SatN{M}{C}\) для деяких\(C \in \Gamma\), або (c)\(\Sat{M}{C}\) для деяких\(C \in \Delta\). У випадку (а),\(\Sat{M}{A \lor B}\). У випадку (б), є\(C \in \Gamma\) таке, що\(\SatN{M}{C}\). У випадку (с), є\(C \in \Delta\) таке, що\(\Sat{M}{C}\). Так що в кожному конкретному випадку\(\Struct{M}\) задовольняє\(\Gamma \Sequent \Delta, A \lor B\), т. Е\(\Theta \Sequent \Xi\). Так як\(\Struct{M}\) був\(\Theta \Sequent \Xi\) довільним, є дійсним. Випадок, з якого\(A \lor B\) виводиться,\(B\) обробляється однаково, змінюючи\(A\) на\(B\).

6. Останній висновок\(\RightR{\lif}\): Потім\(\pi\) закінчується в

   

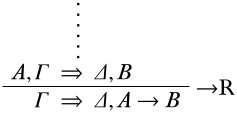
   Знову ж таки, індукційна гіпотеза говорить, що передумова є дійсною; ми хочемо показати, що висновок також дійсний. \(\Struct{M}\)Дозволяти бути довільним. Оскільки\(A, \Gamma \Sequent \Delta, B\) дійсний, принаймні один із наступних випадків отримує: (a)\(\SatN{M}{A}\), (b)\(\Sat{M}{B}\), (c)\(\SatN{M}{C}\) для деяких\(~C \in \Gamma\) або (d)\(\Sat{M}{C}\) для деяких\(C \in \Delta\). У випадках (а) і (б),\(\Sat{M}{A \lif B}\) і так є\(C \in \Delta, A \lif B\) таке, що\(\Sat{M}{C}\). У випадку (c), для деяких\(C \in \Gamma\),\(\SatN{M}{C}\). У випадку (d), для деяких\(C \in \Delta\),\(\Sat{M}{C}\). У кожному конкретному випадку\(\Struct{M}\) задовольняє\(\Gamma \Sequent \Delta, A \lif B\). Так як\(\Struct{M}\) був\(\Gamma \Sequent \Delta, A \lif B\) довільним, є дійсним.

7. Останній висновок\(\LeftR{\lforall{}{}}\): Тоді існує формула\(A(x)\) і закритий термін,\(t\) такий, який\(\pi\) закінчується

   

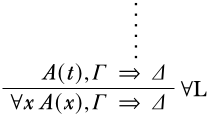
   Хочемо показати, що висновок\(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\) дійсний. Розглянемо структуру\(\Struct M\). Оскільки передумова\(A(t), \Gamma \Sequent \Delta\) є дійсною, (а)\(\SatN{M}{A(t)}\), (b)\(\SatN{M}{C}\) для деяких\(C \in \Gamma\), або (c)\(\Sat{M}{C}\) для деяких\(C \in \Delta\). У випадку (а), за пропозицією 5.14.4, якщо\(\Sat{M}{\lforall{x}{A(x)}}\), то\(\Sat{M}{A(t)}\). З тих пір\(\SatN{M}{A(t)}\),\(\SatN{M}{\lforall{x}{A(x)}}\). У випадку (b) і (c),\(\Struct{M}\) також задовольняє\(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\). Так як\(\Struct M\) був\(\lforall{x}{A(x)}, \Gamma \Sequent \Delta\) довільним, є дійсним.

8. Останній висновок\(\RightR{\lexists{}{}}\): Вправа.

9. Останній висновок\(\RightR{\lforall{}{}}\): Тоді є формула\(A(x)\) і постійний символ,\(a\) такий, який\(\pi\) закінчується

   

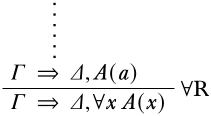
   де виконується умова власної змінної, тобто\(a\) не зустрічається в\(A(x)\)\(\Gamma\), або\(\Delta\). За індукційною гіпотезою, передумова останнього висновку є дійсною. Ми повинні показати, що висновок також дійсний, тобто, що для будь-якої структури\(\Struct M\), (a)\(\Sat{M}{\lforall{x}{A(x)}}\), (b)\(\SatN{M}{C}\) для деяких\(C \in \Gamma\), або (c)\(\Sat{M}{C}\) для деяких\(C \in \Delta\).

   Припустимо,\(\Struct{M}\) це довільна структура. Якщо (b) або (c) тримає, ми зробили, тому припустимо, що ні тримає: для всіх\(C \in \Gamma\)\(\Sat{M}{C}\), і для всіх\(C \in \Delta\),\(\SatN{M}{C}\). Ми повинні показати, що (а) тримає, тобто\(\Sat{M}{\lforall{x}{A(x)}}\). За пропозицією 5.12.4, якщо достатньо, щоб показати, що\(\Sat[,s]{M}{A(x)}\) для всіх присвоєнь змінних\(s\). Так що давайте\(s\) довільна змінна присвоєння. Розглянемо структуру\(\Struct{M'}\), яка так само, як\(\Struct{M}\) крім\(\Assign{a}{M'} = s(x)\). За наслідком 5.13.1, для будь-якого\(C \in \Gamma\),\(\Sat{M'}{C}\) так як\(a\) не відбувається в\(\Gamma\), і для будь-якого\(C \in \Delta\),\(\SatN{M'}{C}\). Але передумова дійсна, так що\(\Sat{M'}{A(a)}\). За пропозицією 5.12.3\(\Sat[,s]{M'}{A(a)}\), оскільки\(A(a)\) є реченням. Тепер\(\varAssign{s}{s}{x}\) з\(s(x) = \Value[s]{a}{M'}\), так як ми\(\Struct{M'}\) визначили саме таким чином. Так Пропозиція 5.13.3 застосовується, і ми отримуємо\(\Sat[,s]{M'}{A(x)}\). Оскільки\(a\) не відбувається в\(A(x)\), за пропозицією 5.13.1,\(\Sat[,s]{M}{A(x)}\). Оскільки\(s\) було довільним, ми завершили доказ того, що\(\Sat[,s]{M}{A(x)}\) для всіх змінних присвоєнь.

10. Останній висновок\(\LeftR{\lexists{}{}}\): Вправа.

Тепер розглянемо можливі висновки з двома приміщеннями.

1. Останній висновок - це розріз: потім\(\pi\) закінчується

   

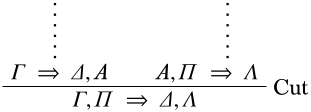
   \(\Struct{M}\)Дозволяти буде будовою. За індукційною гіпотезою приміщення є дійсними, тому\(\Struct{M}\) задовольняє обидва приміщення. Розрізняємо два випадки: (а)\(\SatN{M}{A}\) і (б)\(\Sat{M}{A}\). У випадку (а), для того,\(\Struct{M}\) щоб задовольнити ліве приміщення, воно повинно задовольнити\(\Gamma \Sequent \Delta\). Але потім це також задовольняє висновок. У випадку (b), щоб\(\Struct{M}\) задовольнити правильне приміщення, воно повинно задовольнити\(\Pi \setminus \Lambda\). Знову\(\Struct{M}\) задовольняє висновок.

2. Останній висновок -\(\RightR{\land}\). Потім\(\pi\) закінчується

   

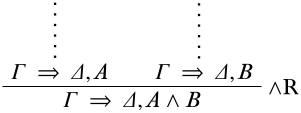
   Розглянемо структуру\(\Struct M\). Якщо\(\Struct{M}\) задовольняє\(\Gamma \Sequent \Delta\), ми закінчили. Отже, припустимо, що це не так, оскільки\(\Gamma \fCenter \Delta, A\) діє за індукційною гіпотезою,\(\Sat{M}{A}\). Аналогічно,\(\Gamma \Sequent \Delta, B\) оскільки діє,\(\Sat{M}{B}\). Але потім\(\Sat{M}{A \land B}\).

3. Останній висновок\(\LeftR{\lor}\): Вправа.

4. Останній висновок -\(\LeftR{\lif}\). Потім\(\pi\) закінчується

   

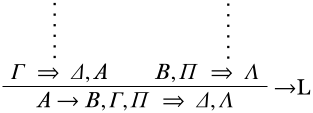
   Знову ж таки, розгляньте структуру\(\Struct{M}\) і припустимо\(\Struct{M}\), що не задовольняє\(\Gamma, \Pi \Sequent \Delta, \Lambda\). Ми маємо це показати\(\SatN{M}{A \lif B}\). Якщо\(\Struct{M}\) не задовольняє\(\Gamma, \Pi \Sequent \Delta, \Lambda\), то ні\(\Gamma \Sequent \Delta\) ні задовольняє\(\Pi \Sequent \Lambda\). Так як,\(\Gamma \Sequent \Delta, A\) дійсно, у нас є\(\Sat{M}{A}\). Так як\(B, \Pi \Sequent \Lambda\) діє, у нас є\(\SatN{M}{B}\). Але потім\(\SatN{M}{A \lif B}\), що ми хотіли показати.

◻

Проблема\(\PageIndex{1}\)

Завершіть доказ теореми\(\PageIndex{1}\).

Слідство\(\PageIndex{1}\)

Якщо\(\Proves A\) тоді\(A\) дійсний.

Слідство\(\PageIndex{2}\)

Якщо\(\Gamma \Proves A\) тоді\(\Gamma \Entails A\).

Доказ. Якщо\(\Gamma \Proves A\) тоді для деякої скінченної\(\Gamma_0 \subseteq \Gamma\) підмножини, існує виведення\(\Gamma_0 \Sequent A\). За теоремою\(\PageIndex{1}\), кожна структура\(\Struct{M}\) або робить щось\(B \in \Gamma_0\) хибним, або робить\(A\) правдою. Отже, якщо\(\Sat{M}{\Gamma}\) тоді і\(\Sat{M}{A}\). ◻

Слідство\(\PageIndex{3}\)

Якщо\(\Gamma\) задовольняється, значить, послідовно.

Доказ. Доводимо контрапозитив. Припустимо, що\(\Gamma\) це не послідовно. Потім відбувається\(\Gamma_0 \subseteq \Gamma\) кінцеве і виведення\(\Gamma_0 \Sequent \quad\). За теоремою\(\PageIndex{1}\),\(\Gamma_0 \Sequent \quad\) є дійсним. Іншими словами, для кожної структури існує\(C \in \Gamma_0\) так\(\Struct{M}\), що\(\SatN{M}{C}\), і з тих пір\(\Gamma_0 \subseteq \Gamma\), що теж\(C\) є в\(\Gamma\). Таким чином, ніщо не\(\Struct{M}\)\(\Gamma\) задовольняє\(\Gamma\), і не задовольняє. ◻