9.6: Похідні з кількісними показниками

Last updated
Save as PDF

Page ID: 52876

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Template:MathJaxZach

Приклад\(\PageIndex{1}\)

Маючи справу з квантифікаторами, ми повинні переконатися, що не порушувати умову власної змінної, а іноді це вимагає від нас пограти з порядком проведення певних висновків. Загалом, це допомагає спочатку спробувати подбати про правила, що підлягають умові власної змінної (вони будуть нижче в готовому доказі).

Давайте подивимося, як ми б дали виведення формули\(\lexists{x}{\lnot A(x)} \lif \lnot \lforall{x}{A(x)}\). Починаючи як зазвичай, пишемо

9.6.1.png

Ми починаємо з того, що записуємо, що потрібно, щоб виправдати цей останній крок за допомогою\(\Intro{\lif}\) правила.

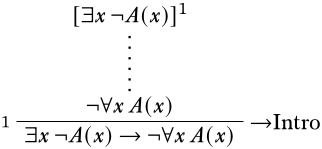
9.6.2.png

Оскільки немає очевидного правила, до якого слід застосувати\(\lnot \lforall{x}{A(x)}\), ми продовжимо налаштування деривації, щоб ми могли використовувати\(\Elim{\lexists{}{}}\) правило. Тут ми повинні звернути увагу на власнузмінну умову, і вибрати константу, яка не з'являється в\(\lexists{x}{A(x)}\) або будь-яких припущеннях, від яких вона залежить. (Оскільки не з'являються постійні символи, однак, будь-який вибір буде робити добре.)

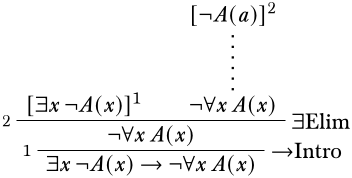
9.6.3.png

Для того, щоб вивести\(\lnot \lforall{x}{A(x)}\), ми спробуємо скористатися\(\Intro{\lnot}\) правилом: це вимагає, щоб ми вивели протиріччя, можливо, використовуючи\(\lforall{x}{A(x)}\) як додаткове припущення. Звичайно, це протиріччя може включати припущення\(\lnot A(a)\), яке буде вичерпано\(\Intro{\lif}\) умовиведенням. Ми можемо налаштувати його наступним чином:

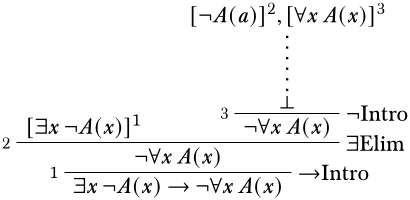
9.6.4.png

Схоже, ми близькі до того, щоб отримати протиріччя. Найпростішим правилом для застосування є те\(\Elim{\lforall{}{}}\), що не має власнихзмінних умов. Оскільки ми можемо використовувати будь-який термін, який ми хочемо замінити універсально кількісно\(x\), є найбільш сенс продовжувати використовувати,\(a\) щоб ми могли досягти протиріччя.

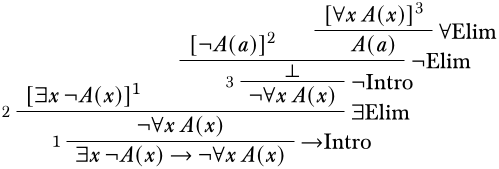
9.6.5.png

Важливо, особливо при роботі з квантифікаторами, двічі перевірити, що власна змінна умова не була порушена. Оскільки єдине правило, яке ми застосували, яке підпорядковується умові власної змінної\(\Elim{\exists}\), було, а власна змінна\(a\) не зустрічається в будь-яких припущеннях, від яких вона залежить, це правильна похідність.

Приклад\(\PageIndex{2}\)

Іноді ми можемо отримати формулу з інших формул. У цих випадках ми можемо мати невичерпні припущення. Важливо відстежувати наші припущення, а також кінцеву мету.

Давайте подивимося, як ми б дали виведення формули\(\lexists{x}{C(x,b)}\) з припущень\(\lexists{x}{(A(x) \land B(x))}\) і\(\lforall{x}{(B(x) \lif C(x,b))}\). Починаючи як завжди, пишемо висновок внизу.

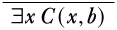
9.6.6.png

У нас є два приміщення для роботи. Для використання першого, тобто спробувати знайти похідне\(\lexists{x}{C(x, b)}\) від\(\lexists{x}{(A(x) \land B(x))}\) ми б скористалися\(\Elim{\lexists{}{}}\) правилом. Оскільки він має власну змінну умову, ми застосуємо це правило в першу чергу. Отримуємо наступне:

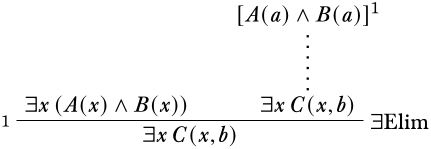
9.6.7.пнг

Два припущення, з якими ми працюємо, поділяють\(B\). На цьому етапі може бути корисно подати заявку\(\Elim{\land}\) на відокремлення\(B(a)\).

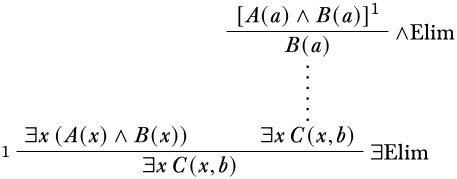
9.6.8.png

Друге припущення, з яким ми маємо працювати, - це\(\lforall{x}{(B(x) \lif C(x,b))}\). Оскільки немає власної змінної умови, ми можемо створити екземпляр\(x\) з постійним символом,\(a\) використовуючи\(\Elim{\lforall{}{}}\) для отримання\(B(a) \lif C(a, b)\). У нас тепер є\(B(a) \lif C(a,b)\) і те, і інше\(B(a)\). Наступним нашим кроком має стати пряме застосування\(\Elim{\lif}\) правила.

9.6.9.png

Ми так близько! Одне застосування\(\Intro{\lexists{}{}}\) і ми досягли своєї мети.

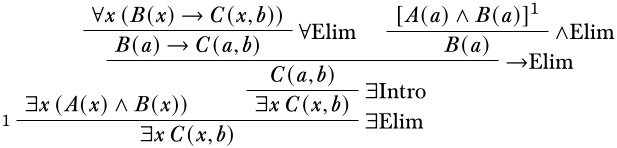
9.6.10.пнг

Так як ми переконалися на кожному кроці, щоб власнізмінні умови не були порушені, то можемо бути впевнені, що це правильна деривація.

Приклад\(\PageIndex{3}\)

Дайте висновок формули\(\lnot\lforall{x}{A(x)}\) з припущень\(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\) і\(\lnot\lexists{y}{B(y)}\). Починаючи як завжди, записуємо цільову формулу внизу.

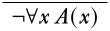
9.6.11.пнг

Останній рядок деривації - заперечення, тому спробуємо скористатися\(\Intro{\lnot}\). Для цього потрібно, щоб ми з'ясували, як вивести протиріччя.

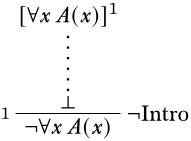
9.6.12.пнг

Поки що добре. Ми можемо використовувати\(\Elim{\lforall{}{}}\), але це не очевидно, чи це допоможе нам досягти нашої мети. Замість цього давайте використаємо одне з наших припущень. \(\lforall{x}{A(x)} \lif \lexists{y}{B(y)}\)разом з\(\lforall{x}{A(x)}\) дозволить нам скористатися\(\Elim{\lif}\) правилом.

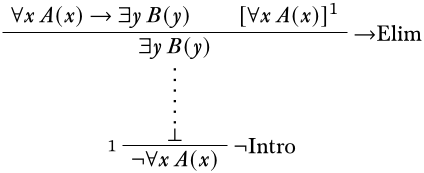
9.6.13.пнг

Тепер у нас є одне остаточне припущення, з яким слід працювати, і, схоже, це допоможе нам досягти протиріччя за допомогою використання\(\Elim{\lnot}\).

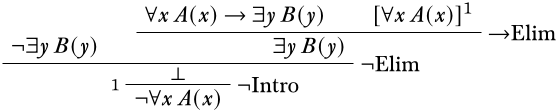
9.6.14.пнг

Проблема\(\PageIndex{1}\)

Дайте похідні такі:

\(\lexists{y}{A(y)} \lif B\)з припущення\(\lforall{x}{(A(x) \lif B)}\)
\(\lexists{x}{(A(x) \lif \lforall{y}{A(y)})}\)