Skip to main content
LibreTexts - Ukrayinska

9.7: Доказно-теоретичні поняття

  1. Last updated
  2. Save as PDF
  • Page ID
    52917

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Template:MathJaxZach

    Подібно до того, як ми визначили низку важливих семантичних понять (валідність, тяговість, задовільність), ми тепер визначаємо відповідні теоретичні поняття. Вони визначаються не апеляцією до задоволення вироків у структурах, а зверненням до похідності або невід'ємності певних речень від інших. Важливим відкриттям було те, що ці поняття збігаються. Те, що вони роблять, - це зміст теорем про обґрунтованість та повноту.

    Визначення\(\PageIndex{1}\): Theorems

    Речення\(A\) - це теорема, якщо є виведення\(A\) в природному відрахуванні, в якому виписані всі припущення. Ми пишемо\(A\),\(\Proves A\) якщо це теорема, а\(\ProvesN A\) якщо це не так.

    Визначення\(\PageIndex{2}\): Derivability

    Речення\(A\) випливає з набору пропозицій\(\Gamma\)\(\Gamma \Proves A\), якщо є похідний з висновком\(A\) і в якому кожне припущення або виписано, або знаходиться в\(\Gamma\). Якщо\(A\) не виводиться з\(\Gamma\) пишемо\(\Gamma \ProvesN A\).

    Визначення\(\PageIndex{3}\): Consistency

    Сукупність пропозицій\(\Gamma\) є непослідовним iff\(\Gamma \Proves \lfalse\). Якщо не\(\Gamma\) є суперечливим, тобто, якщо\(\Gamma \ProvesN \lfalse\), ми говоримо, що це послідовно.

    Пропозиція\(\PageIndex{1}\): Reflexivity

    Якщо\(A \in \Gamma\), то\(\Gamma \Proves A\).

    Доказ. Саме\(A\) по собі припущення є виведенням того,\(A\) де знаходиться кожне нерозряджене припущення (тобто\(A\))\(\Gamma\). ◻

    Пропозиція\(\PageIndex{2}\): Monotony

    Якщо\(\Gamma \subseteq \Delta\) і\(\Gamma \Proves A\), то\(\Delta \Proves A\).

    Доказ. Будь-яке\(\Gamma\) похідне\(A\) від також є виведенням\(A\) від\(\Delta\). ◻

    Пропозиція\(\PageIndex{3}\): Transitivity

    Якщо\(\Gamma \Proves A\) і\(\{A\} \cup \Delta \Proves B\), то\(\Gamma \cup \Delta \Proves B\).

    Доказ. Якщо\(\Gamma \Proves A\), є виведення\(\delta_0\) з усіма\(A\) нерозрядженими припущеннями в\(\Gamma\). Якщо\(\{A\} \cup \Delta \Proves B\), то відбувається виведення\(\delta_1\) з усіма\(B\) нерозрядженими припущеннями в\(\{A\} \cup \Delta\). Тепер розглянемо:

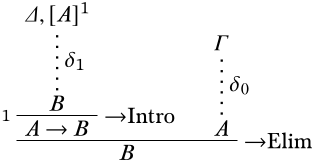
    9.7.1.PNG

    Нерозряджені припущення зараз всі серед\(\Gamma \cup \Delta\), так що це показує\(\Gamma \cup \Delta \Proves B\). ◻

    Коли\(\Gamma = \{A_1, A_2, \ldots, A_k\}\) є кінцевим множиною, ми можемо використовувати спрощене позначення\(A_1,A_2,\ldots,A_k \Proves B\) для\(\Gamma \Proves B\), зокрема\(A \Proves B\) означає, що\(\{A\} \Proves B\).

    Зверніть увагу, що якщо\(\Gamma \Proves A\) і\(A \Proves B\), то\(\Gamma \Proves B\). Звідси випливає також, що якщо\(A_1, \dots, A_n \Proves B\) і\(\Gamma \Proves A_i\) для кожного\(i\), то\(\Gamma \Proves B\).

    Пропозиція\(\PageIndex{4}\)

    Наступні є рівнозначними.

    1. \(\Gamma\)є непослідовним.

    2. \(\Gamma \Proves {A}\)за кожне речення\({A}\).

    3. \(\Gamma \Proves {A}\)і\(\Gamma \Proves \lnot {A}\) для деякого речення\({A}\).

    Доказ. Вправа. ◻

    Проблема\(\PageIndex{1}\)

    Доведіть пропозицію\(\PageIndex{4}\).

    Пропозиція\(\PageIndex{5}\): Compactness

    1. Якщо\(\Gamma \Proves A\) тоді є кінцева підмножина\(\Gamma_0 \subseteq \Gamma\) така, що\(\Gamma_0 \Proves A\).

    2. Якщо кожна скінченна підмножина\(\Gamma\) послідовна,\(\Gamma\) то послідовна.

    Доказ.

    1. Якщо\(\Gamma \Proves A\), то відбувається виведення\(\delta\)\(A\) з\(\Gamma\). \(\Gamma_0\)Дозволяти бути безліччю нерозряджених припущень\(\delta\). Оскільки будь-яке похідне є кінцевим,\(\Gamma_0\) може містити лише скінченно багато речень. Отже,\(\delta\) є виведенням\(A\) від кінцевого\(\Gamma_0 \subseteq \Gamma\).

    2. Це контрапозитив (1) для особливого випадку\(A \ident \lfalse\).

    ◻