Skip to main content
LibreTexts - Ukrayinska

1.7: Імовірності в генетиці

  1. Last updated
  2. Save as PDF
  • Page ID
    7567

    • \( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

    Вступ

    Квадрат Punnett є цінним інструментом, але він не ідеально підходить для кожної проблеми генетики. Наприклад, припустимо, що вас попросили обчислити частоту рецесивного класу не для хреста Aa x Aa, не для хреста AaB x AaBb, а для хреста AabBccdDee x AabBccdDee. Якщо ви хотіли вирішити це питання за допомогою площі Паннетта, ви могли б це зробити - але вам потрібно буде заповнити квадрат Паннетта з 1024 коробками. Напевно, не те, що ви хочете намалювати під час іспиту, або в будь-який інший час, якщо ви можете допомогти йому!

    П'ять генів проблема вище стає менш залякуючим, як тільки ви зрозумієте, що квадрат Пуннетта - це лише візуальний спосіб представлення обчислень ймовірності. Хоча це чудовий інструмент, коли ви працюєте з одним або двома генами, він може стати повільним і громіздким, коли число зростає. У якийсь момент стає швидше (і менш схильним до помилок) просто робити обчислення ймовірності самостійно, без візуального представлення незграбного квадрата Паннетта. У всіх випадках розрахунки та квадрат дають однакову інформацію, але, маючи обидва інструменти на поясі, ви можете бути готові обробляти більш широкий спектр проблем більш ефективним способом.

    У цій статті ми розглянемо деякі основи ймовірності, включаючи те, як обчислити ймовірність двох незалежних подій, що відбуваються (подія X і подія Y) або ймовірність будь-якої з двох взаємовиключних подій (подія X або подія Y). Потім ми побачимо, як ці розрахунки можуть бути застосовані до проблем генетики, і, зокрема, як вони можуть допомогти вам вирішити проблеми, пов'язані з відносно великою кількістю генів.

    [Рішення п'ятигенної перехресної проблеми]

    У цій задачі ми повинні знайти частоту рецесивного класу серед потомства хреста AABBccdddee x AABBcccdddee - тобто частоту осіб aabbcccdddee. Як ми можемо отримати індивіда aabbccddee? Для цього є лише один спосіб: обоє батьків повинні внести абцидну гамету.

    Яка ж тоді ймовірність того, що хтось із батьків зробить абдедовую гамет? Обидва батьки гетерозиготні для всіх п'яти генів, тому є 1/2 шансів отримати рецесивний (нижній регістр) аллель для будь-якого одного гена. Щоб отримати бажану гамету, нам потрібні всі п'ять генів в рецесивній формі (a і b і c і d і e). Це випадок, коли ми можемо застосувати правило продукту, яке стверджує, що ймовірність події X і події Y відбувається є добутком їх індивідуальних ймовірностей (ймовірність X разів ймовірності Y), припускаючи, що X і Y є незалежними подіями. Таким чином, загальна ймовірність того, що один з батьків виробляє абцидний гамет становить:

    Імовірність абцодної гамети = (ймовірність a) x (ймовірність b) x (ймовірність c) x (ймовірність d) x (ймовірність e)

    \(P(abcde)=P(a)\cdot P(b)\cdot P(c)\cdot P(d)\cdot P(e)\)

    \(P(abcde)=(1/2)\cdot (1/2)\cdot (1/2)\cdot (1/2)\cdot (1/2)=(1/2)^5=1/32\)

    Якщо це ймовірність того, що один з батьків зробить abcde gamete, яка ймовірність того, що обидва батьки це роблять? Знову ж таки, ми можемо застосувати правило «і» (правило продукту), оскільки нам потрібно як батько 1, так і батько 2, щоб зробити abcde gamete, щоб отримати нашу цільову рецесивну гомозиготу. Таким чином, загальна ймовірність становить:

    Імовірність aabbccddee індивіда = (ймовірність того, що батько 1 робить абцидну гамету) (ймовірність того, що батько 2 робить абкод гамети)

    \(P(aabbccddee)=P(abcde_\text{parent A})\cdot P(abcde_\text{parent B})\)

    \(P(aabbccddee)=(1/32)\cdot (1/32)=1/1024\)

    Це наша загальна ймовірність рецесивної гомозиготи для всіх п'яти генів.

    Імовірність 1/1024 відповідає 1 коробці з 1024 коробок квадрата Пуннетта, яку ви повинні намалювати, щоб представити цей хрест. Розрахунок ймовірності - це той самий розрахунок, який ми б неявно зробили, малюючи квадрат Пуннетта, просто швидше і з меншими шансами на помилки.

    Основи ймовірності

    Ймовірності - це математичні міри ймовірності. Іншими словами, вони є способом кількісної оцінки (даючи конкретне, числове значення), наскільки ймовірно, що щось трапиться. Імовірність 1 для події означає, що вона гарантовано відбудеться, тоді як ймовірність 0 для події означає, що вона гарантовано не відбудеться. Простий приклад ймовірності - це 1/2 шансу отримати голови, коли ви перевертаєте монету, як пояснює Сал у цьому вступі до ймовірності відео.

    Ймовірності можуть бути або емпіричними, тобто вони обчислюються з реальних спостережень, або теоретичними, що означає, що вони прогнозуються за допомогою набору правил або припущень.

    • Емпірична ймовірність події обчислюється підрахунком кількості разів, коли ця подія відбувається, і діливши її на загальну кількість разів, коли ця подія могла статися. Наприклад, якщо подія, яку ви шукали, була зморшкуватим насінням гороху, і ви бачили його 1850 разів із 7 324 загального насіння, яке ви досліджували, емпірична ймовірність отримання зморшкуватого насіння становила б 1,850/7,324 = 0,253, або дуже близько до 1 на 4 насіння.
    • Теоретична ймовірність події розраховується на основі інформації про правила і обставини, які виробляють подію. Він відображає кількість разів, коли подія, як очікується, відбудеться відносно кількості разів, коли вона могла статися. Наприклад, якби у вас була рослина гороху гетерозиготна для гена форми насіння (Rr) і дозвольте їй самозапліднюватися, ви могли б скористатися правилами ймовірності та своїми знаннями генетики, щоб передбачити, що 1 з кожних 4 потомства отримає два рецесивні алелі (rr) і здасться зморшкуватими, що відповідає ймовірності 0,25 (1/4). Детальніше нижче ми поговоримо про те, як застосовувати правила ймовірності в цьому випадку.

    Взагалі, чим більша кількість точок даних, які використовуються для обчислення емпіричної ймовірності, таких як форми окремих насіння гороху, тим ближче вона буде наближатися до теоретичної ймовірності.

    Правило продукту

    Одне правило ймовірності, яке дуже корисно в генетиці, є правило продукту, яке стверджує, що ймовірність двох (або більше) незалежних подій, що відбуваються разом, можна обчислити шляхом множення індивідуальних ймовірностей подій. Наприклад, якщо ви один раз кидаєте шестигранну матрицю, у вас є шанс 1/6 отримати шістку. Якщо ви кидаєте дві кістки відразу, ваш шанс отримати дві шістки: (ймовірність шести на померти 1) х (ймовірність шести на померти 2) = (1/6) ⋅ (1/6) = 1/36.

    Загалом, ви можете думати про правило продукту як правило «і»: якщо і подія X, і подія Y повинні відбутися для того, щоб відбувся певний результат, і якщо X і Y незалежні один від одного (не впливають на ймовірність один одного), то ви можете використовувати правило продукту для обчислення ймовірності результат шляхом множення ймовірностей X і Y.

    Ми можемо використовувати правило продукту для прогнозування частот подій запліднення. Наприклад, розглянемо щось середнє між двома гетерозиготними (Aa) особинами. Які шанси отримати особистість в наступному поколінні? Єдиний спосіб отримати індивіда - це якщо мати вносить гамет, а батько вносить гамет. Кожен батько має 1/2 шансу зробити гамет. Таким чином, шанс появи потомства аа становить: (ймовірність того, що мати внесе а) х (ймовірність того, що батько внесе а) = (1/2) ⋅ (1/2) = 1/4.

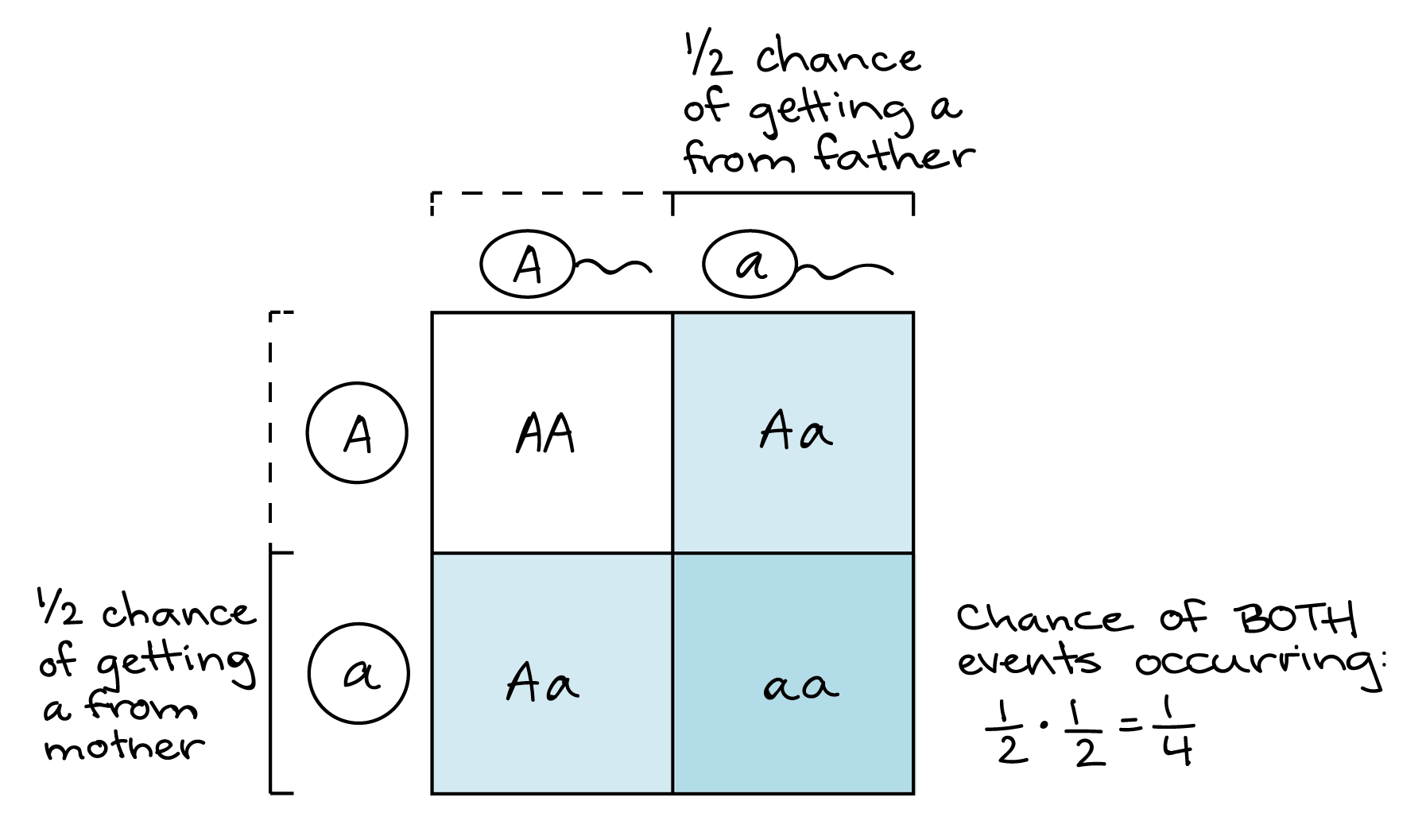
    Ілюстрація того, як квадрат Пуннетта може представляти правило продукту. Площа Пуннетта: ||A|A-|-|-|-A||AA|**AA**AA||_AA_|***AA*** Існує 1/2 шансу отримати алель від батьків-чоловіків, що відповідає крайньому правому стовпчику квадрата Пуннетта. Аналогічно, є 1/2 шанс отримати алель від материнського батька, що відповідає самому нижньому ряду площі Пуннетта. Перетин цих рядків і стовпців, що відповідають нижньому правому полі таблиці, представляє ймовірність отримання алеля від материнського батька і батьківського батька (1 з 4 ящиків у квадраті Пуннетта, або 1/4 шансу).

    Це той самий результат, який ви отримаєте з квадратом Пуннетта, і насправді той самий логічний процес, а також - те, що зайняло у мене роки, щоб зрозуміти! Єдина відмінність полягає в тому, що в квадраті Пуннетта ми будемо робити розрахунок візуально: ми представляємо 1/2 ймовірності гамети від кожного батька як один з двох стовпців (для батька) і один з двох рядків (для матері). 1-квадратний перетин стовпця та рядка (із загальних квадратів 4 таблиці) представляє 1/4 шансу отримати a від обох батьків.

    Правило ймовірності суми

    У деяких генетичних проблемах може знадобитися обчислити ймовірність того, що відбудеться якесь одне з декількох подій. У цьому випадку вам потрібно буде застосувати інше правило ймовірності - правило суми. Згідно з правилом суми, ймовірність того, що відбудеться будь-яка з декількох взаємовиключних подій, дорівнює сумі індивідуальних ймовірностей подій.

    Наприклад, якщо ви кидаєте шестигранну матрицю, у вас є шанс 1/6 отримати будь-яке задане число, але ви можете отримати лише одне число за рулон. Ви ніколи не можете отримати як один, так і шість одночасно; ці результати є взаємовиключними. Таким чином, шанси отримати або одиницю, або шістку такі: (ймовірність отримання 1) + (ймовірність отримання 6) = (1/6) + (1/6) = 1/3.

    Правило суми можна вважати правилом «або»: якщо результат вимагає, щоб відбулася або подія X, або подія Y, а якщо X і Y є взаємовиключними (якщо в даному випадку може статися тільки той чи інший), то ймовірність результату можна обчислити, додавши ймовірності X і Y.

    Як приклад, давайте використаємо правило суми, щоб передбачити частку потомства від хреста Aa x Aa, який матиме домінантний фенотип (генотип AA або Aa). У цьому хресті є три події, які можуть привести до домінантного фенотипу:

    • Зустрічаються дві гамети А (даючи генотип АА), або
    • Гамета від мами зустрічає гамет від тата (даючи генотип Аа), або
    • гамета від мами зустрічає гамет від тата (даючи генотип Аа)

    У будь-якому одному випадку запліднення може виникнути лише одна з цих трьох можливостей (вони є взаємовиключними).

    Оскільки це ситуація «або», коли події взаємовиключні, ми можемо застосувати правило суми. Використовуючи правило продукту, як ми робили вище, ми можемо виявити, що кожна окрема подія має ймовірність 1/4. Отже, ймовірність потомства з домінуючим фенотипом становить: (Імовірність А від мами і А від тата) + (ймовірність А від мами і а від тата) + (ймовірність а від мами і А від тата) = (1/4) + (1/4) + (1/4) = 3/4.

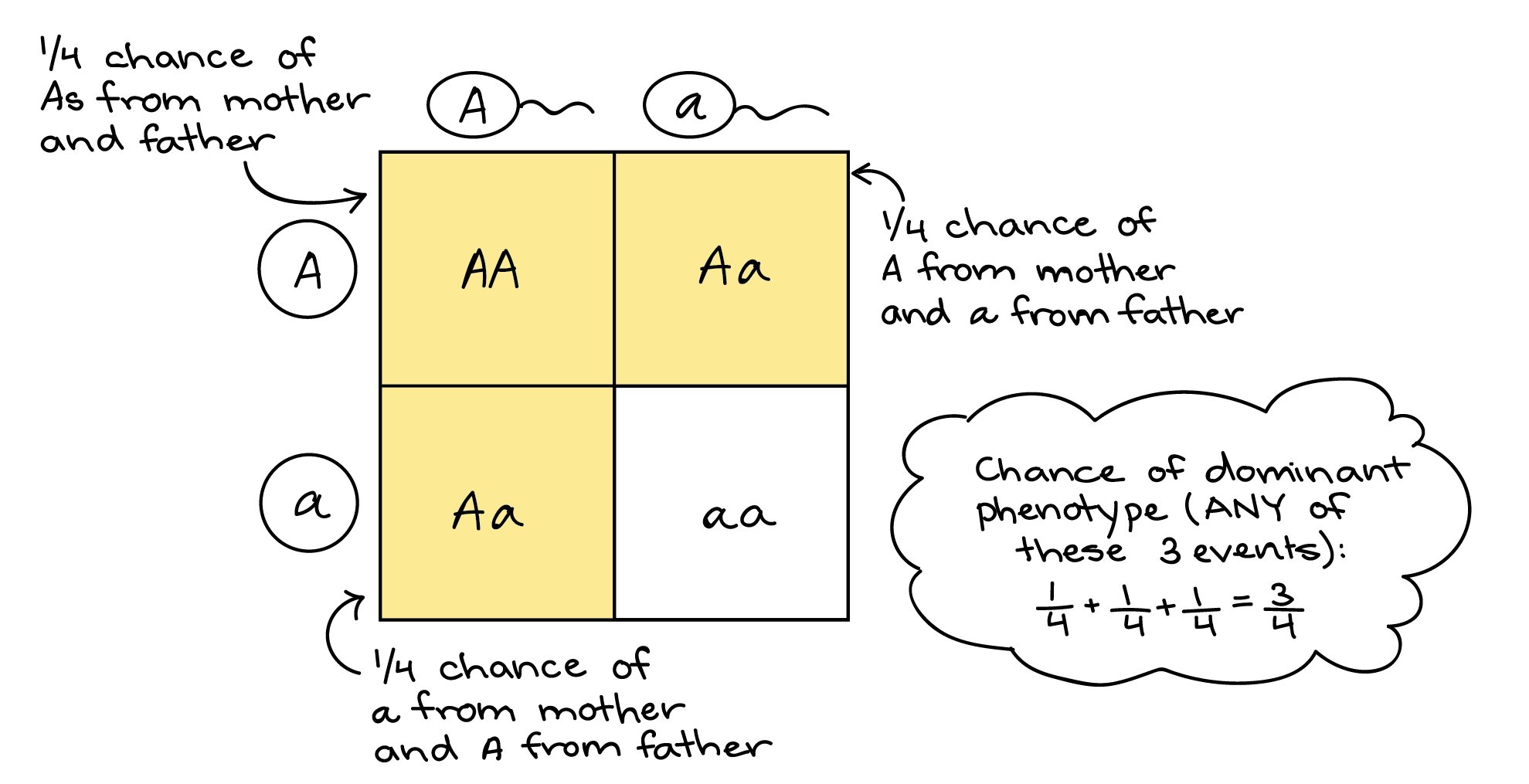
    Ілюстрація того, як квадрат Пуннетта може представляти правило суми. Квадрат Пуннетта: ||A|A-|-|-|-A||**AA**AA**AA||**AA**AA**|AA**жирний** ящики представляють події, які призводять до домінантного фенотипу (генотипу AA або Aa). В одному сперматозоїд А поєднується з яйцеклітиною А. В іншому сперматозоїд А поєднується з яйцеклітиною, а в третині сперматозоїд поєднується з яйцеклітиною А. Кожна подія має 1/4 шансів відбутися (1 з 4 ящиків на площі Пуннетта). Шанс того, що відбудеться будь-яке з цих трьох подій, становить 1/4+1/4+1/4 = 3/4.

    Знову ж таки, це той самий результат, який ми отримаємо з квадратом Punnett. Одна з чотирьох коробок площі Пуннетта тримає домінуючу гомозиготу, АА. Ще дві коробки представляють гетерозиготи, одна з материнською A і батьківською a, інша з протилежною комбінацією. Кожна коробка - це 1 з 4 коробок у всій площі Паннетта, і оскільки коробки не перекриваються (вони взаємовиключні), ми можемо скласти їх (1/4 + 1/4 + 1/4 = 3/4), щоб отримати ймовірність потомства з домінуючим фенотипом.

    Правило добутку та правило суми

    Правило продукту Правило суми
    Для незалежних подій X і Y ймовірність (\(P\)) з них обох зустрічаються (X і Y) дорівнює\(P(X)\cdot P(Y)\). Для взаємовиключних подій X і Y ймовірність (\(P\)), що один відбудеться (X або Y) дорівнює\(P(X)+P(Y)\).

    Застосування правил ймовірності до дигібридних схрещувань

    Прямий розрахунок ймовірностей не має великої переваги перед квадратами Паннетта для сценаріїв успадкування одного гена. (Насправді, якщо ви віддаєте перевагу вчитися візуально, ви можете знайти прямий розрахунок складніше, ніж простіше.) Однак, де вірогідності світяться, коли ви дивитеся на поведінку двох, а то й більше генів.

    Наприклад, уявімо, що ми розводимо двох собак з генотипом BBcc, де домінантний алель B визначає чорний колір шерсті (проти b, жовтий колір шерсті), а домінантний алель C визначає пряме хутро (проти c, кучеряве хутро). Припускаючи, що два гени асортуються незалежно і не пов'язані з сексом, як ми можемо передбачити кількість цуценят BBCC серед потомства?

    Один з підходів полягає в тому, щоб намалювати 16-квадратний квадрат Punnett. Для хреста, що включає два гени, квадрат Пуннетта все ще є гарною стратегією. Крім того, ми можемо використовувати техніку ярлика, що включає чотири квадрати Punnett квадратів і невелике застосування правила продукту. У цій техніці ми розбиваємо загальне питання на два менших питання, кожне з яких стосується іншої генетичної події:

    1. Яка ймовірність отримання генотипу Bb?
    2. Яка ймовірність отримання генотипу Cc?

    Для того, щоб щеня мав генотип BBCc, повинні відбутися обидві ці події: щеня повинен отримувати алелі Bb, і він повинен отримувати алелі Cc. Ці дві події є незалежними, оскільки гени самостійно сортують (не впливають на спадщину один одного). Отже, як тільки ми обчислимо ймовірність кожної генетичної події, ми можемо помножити ці ймовірності, використовуючи правило продукту, щоб отримати ймовірність генотипу інтересу (bbCC).

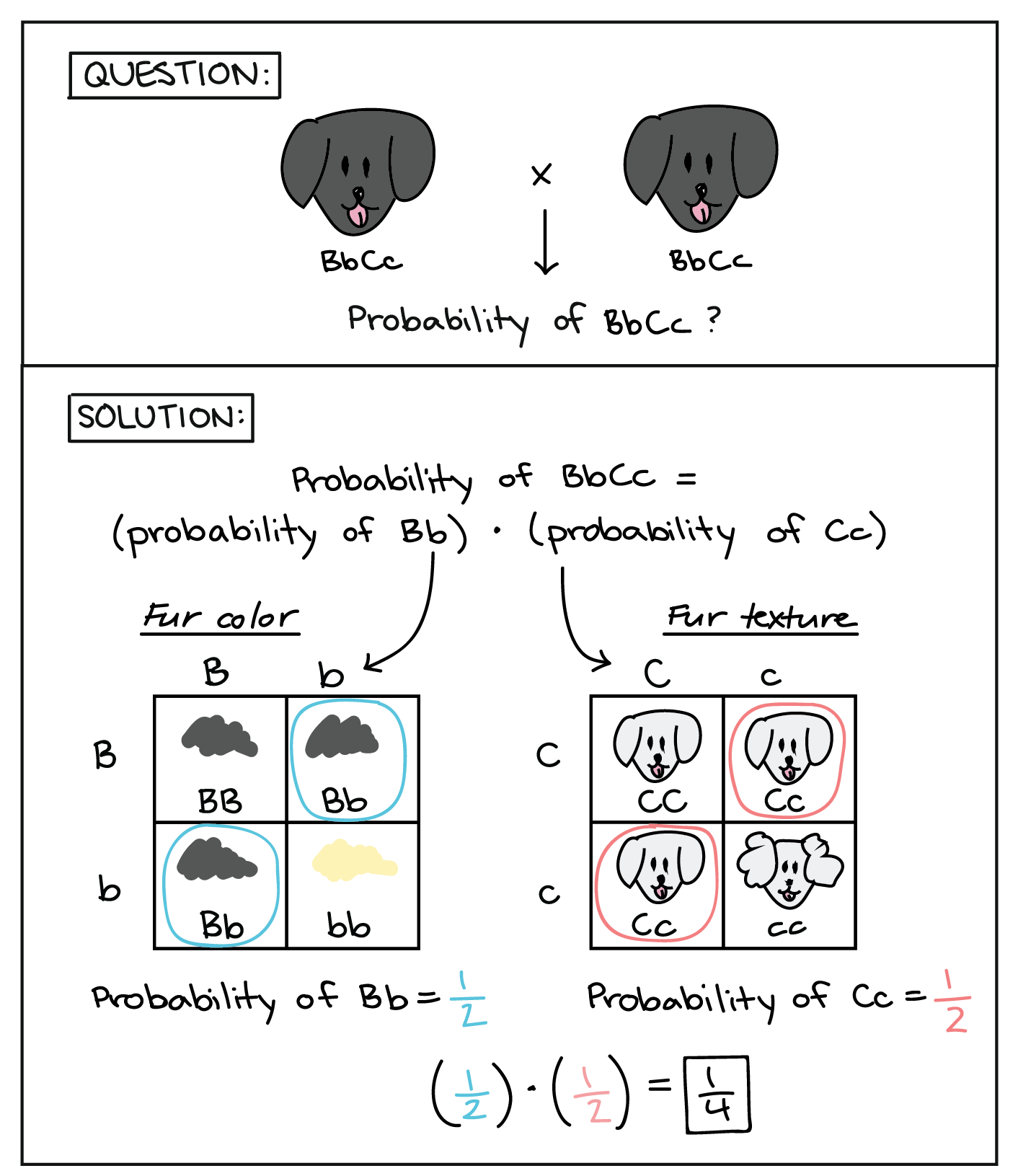
    Діаграма, що ілюструє, як 2X2 квадрати Пуннетта можуть бути використані спільно з правилом добутку для визначення ймовірності певного генотипу в дигібридному хресті. Верхня панель: Питання: коли схрещуються дві собаки BBcc, яка ймовірність отримати особину нащадків BBCC? Нижня панель: Рішення: ймовірність bbCc = (ймовірність Bb) x (ймовірність Cc). Квадрат Пуннетта для забарвлення хутра: ||B|B-|-|-|-B||BB|**BB**B||**BB**|BB Імовірність генотипу Bb: 1/2. Квадрат Пуннетта для текстури хутра: ||C|C-|-|-|-C||CC|**CC**C|||**CC**|CC Ймовірність генотипу Cc: 1/2. Імовірність bbCc = (ймовірність Bb) x (ймовірність Cc). Імовірність BBCC = (1/2) х (1/2) = 1/4

    Щоб обчислити ймовірність отримання генотипу Bb, ми можемо намалювати 4-квадратний квадрат Пуннетта, використовуючи алелі батьків лише для гена кольору шерсті, як показано вище. Використовуючи квадрат Пуннетта, можна помітити, що ймовірність генотипу Bb дорівнює 1/2. (Крім того, ми могли б обчислити ймовірність Bb, використовуючи правило продукту для внесків гамет від двох батьків та правило суми для двох комбінацій гамет, які дають Bb.) Використовуючи подібний квадрат Punnett для алелей текстури хутра батьків, ймовірність отримання генотипу Cc також становить 1/2. Щоб отримати загальну ймовірність генотипу bbCC, ми можемо просто помножити дві ймовірності, даючи загальну ймовірність 1/4.

    [Давайте перевіримо, що з квадратом Punnett]

    16-квадратний квадрат Пуннетта, що ілюструє те ж рішення, досягнуте за допомогою методу ймовірності. ||БК|БК|БК|БК-|-|-|-|-|-БК||ББК|ББК|ББК|**ББК||ББКК||ББКК|**BBCC**|BBCC||BBCC**|BBCC**|BBCC|Фракція потомства геногену**BBCC** тип: 4/16 = 1/4

    Ви також можете використовувати цю техніку для прогнозування частот фенотипу. Дайте йому спробувати в питанні практики нижче!

    Перевірте своє розуміння

    Запит\(\PageIndex{1}\)

    Activity
    [Підказка]

    Ми можемо розбити питання на два менших питання:

    1. Яка частка потомства матиме чорне забарвлення шерсті?
    2. Яку частку потомства матиме пряме хутро?

    Оскільки чорний колір шерсті та пряме хутро є домінуючими рисами, всі цуценята BB та Bb матимуть чорні шуби, а всі цуценята CC та Cc матимуть пряме хутро, відповідне 3/4 цуценят у кожному випадку. (Ви можете намалювати окремі квадрати Punnett для генів кольору та текстури, щоб підтвердити ці частоти.)

    Щоб отримати ймовірність того, що щеня має як чорний колір шерсті, так і пряму шерсть, можна помножити ймовірності цих двох самостійних подій:\((3/4)\cdot(3/4)=9/16\).

    9/16 цуценят матимуть чорні шуби і пряме хутро.

    Поза дигібридними кросами

    Метод ймовірності є найбільш потужним (і корисним) у випадках, пов'язаних з великою кількістю генів.

    Наприклад, уявіть собі щось середнє між двома особами з різними алелями чотирьох незв'язаних генів: AABBcCDD x AabBCCdd. Припустимо, ви хотіли з'ясувати ймовірність отримання потомства з домінуючим фенотипом за всіма чотирма ознаками. На щастя, ви можете застосувати ту саму логіку, що і у випадку з дигібридними кросами вище. Щоб мати домінантний фенотип за всіма чотирма ознаками, і організм повинен мати: одну або кілька копій домінантного аллеля А і одну або кілька копій домінантного алелю В і одну або кілька копій домінантного алелю С і одну або кілька. копії домінантного аллеля D.

    Оскільки гени не пов'язані, це чотири незалежні події, тому ми можемо обчислити ймовірність для кожного, а потім помножити ймовірності, щоб отримати ймовірність загального результату.

    • Імовірність отримання однієї або декількох копій домінуючого Алеля дорівнює 3/4. (Намалюйте квадрат Punnett для Aa x Aa, щоб підтвердити для себе, що 3 з 4 квадратів - це AA або Aa.)
    • Імовірність отримання однієї або декількох копій домінантного В-алеля становить 1/2. (Намалюйте квадрат Punnett для Bb x bb: ви виявите, що половина потомства - Bb, а інша половина bb.)
    • Імовірність отримання однієї або декількох копій домінуючого С алеля дорівнює 1. (Якщо один з батьків гомозиготний КК, немає можливості отримати потомство без алелю С!)
    • Імовірність отримання однієї або декількох копій домінантного D алеля становить 1/2, як для В. (Половина потомства буде Dd, а інша половина - dd.)

    Щоб отримати загальну ймовірність потомства з домінуючим фенотипом для всіх чотирьох генів, ми можемо помножити ймовірності чотирьох незалежних подій:\((3/4)\cdot(1/2)\cdot(1)\cdot(1/2)=3/16\).

    Перевірте своє розуміння

    Запит\(\PageIndex{2}\)

    Activity
    [Підказка]

    Неможливо отримати чотиримісний гомозиготний рецесивний індивід з цього хреста. Це тому, що ймовірність отримання двох рецесивних алелей дорівнює нулю. Перший батько має лише домінантні алелі для цього гена, гарантуючи, що кожен з потомства отримає принаймні один домінантний алель С (і, таким чином, не може відображати рецесивний фенотип).

    Як математично нульова ймовірність фігури генотипу cc? Щоб отримати загальну ймовірність генотипу aabbccdd, нам доведеться помножити ймовірності бажаних генотипів для інших трьох генів (aa, 1/4; bb, 1/2; і dd, 1/2) на нуль, що відповідає генотипу cc, даючи загальний ймовірність нуля.

    \(P(aabbccdd)=P(aa) \cdot P(bb) \cdot P(cc) \cdot P(dd)\)

    \(P(aabbccdd)=(1/4)\cdot(1/2)\cdot(0)\cdot(1/2)=0\)

    Імовірність отримання індивіда з рецесивним фенотипом для всіх чотирьох генів дорівнює 0.

    Дописувачі та атрибуція

    [Атрибуція та посилання]

    Зазначення авторства:

    Ця стаття є модифікованою похідною наступних статей:

    Змінена стаття ліцензується за ліцензією CC BY-NC-SA 4.0.

    Додаткові посилання:

    Гріффітс, А.Дж., Міллер, Дж., Сузукі, Д., Левонтін, Р.К., і Гельбарт, W.M. (2000). Використання генетичних співвідношень. Вступ до генетичного аналізу (7-е видання). Нью-Йорк, Нью-Йорк: Фрімен. Отримано з http://www.ncbi.nlm.nih.gov/books/NBK21812/.

    Первс, В.К., Садава, Д., Оріанс, Г.Х., і Хеллер, Г.К. (2003). Квадрати Пеннетта або обчислення ймовірностей: Вибір методів. У житті: Наука біології (7-е изд., с. 195-196). Сандерленд, Массачусетс: Sinauer Associates.

    Ріс, Дж. Б., Уррі, Л.А., Каїн, М.Л., Вассерман, С.А., Мінорський, П.В., і Джексон, Р.Б. (2011). Мендель і генна ідея. У біології Кемпбелла (10-е видання, стор. 267-291). Сан-Франциско, Каліфорнія: Пірсон.

    Ворон, П.Х., Джонсон, Г.Б., Мейсон, К.А., Лосос, Дж. Б., і Сінгер, С.Р. (2014). Шаблони спадкування. У біології (10-е изд., А.П., с. 221-238). Нью-Йорк, Нью-Йорк: Макгроу-Хілл.

    Староцик А. Квадратний калькулятор Punnett. У науці Primer.com. Отримано з http://scienceprimer.com/punnett-square-calculator.

    Проект Адапа. (2014, 13 серпня). Які закони сегрегації і незалежного асортименту і чому вони так важливі? У Біокнизі. Отримано з https://adapaproject.org/bbk_temp/tiki-index.php?page=Leaf%3A+What+are+the+laws+of+segregation+and+independent+assortment+and+why+are+they+so+important%3F.