3.3: Правила диференціації
- Page ID
- 62278
- Створіть постійну, постійну кратну та владу правила.
- Застосовуйте правила суми та різниці для об'єднання похідних.
- Використовуйте правило добутку для знаходження похідної добутку функцій.
- Використовуйте часткове правило для знаходження похідної частки функцій.
- Розширте правило потужності на функції з негативними показниками.
- Об'єднайте правила диференціації, щоб знайти похідну полінома або раціональної функції.
Пошук похідних функцій за допомогою визначення похідної може бути тривалим і, для певних функцій, досить складним процесом. Наприклад, раніше ми виявили, що
\[\dfrac{d}{dx}\left(\sqrt{x}\right)=\dfrac{1}{2\sqrt{x}} \nonumber \]
за допомогою процесу, який передбачав множення виразу на сполучений перед оцінкою межі.
Процес, який ми могли б використовувати для оцінки\(\dfrac{d}{dx}\left(\sqrt[3]{x}\right)\) за допомогою визначення, хоча і схожий, складніший.
У цьому розділі ми розробляємо правила пошуку похідних, які дозволяють обійти цей процес. Починаємо з основ.
Основні правила
Функції\(f(x)=c\) і\(g(x)=x^n\) де\(n\) - натуральне ціле число - це будівельні блоки, з яких будуються всі поліноми і раціональні функції. Щоб ефективно знаходити похідні поліномів і раціональних функцій, не вдаючись до граничного визначення похідної, потрібно спочатку розробити формули для диференціації цих основних функцій.
Постійне правило
Спочатку застосуємо граничне визначення похідної, щоб знайти похідну від постійної функції,\(f(x)=c\). Для цієї функції обидва\(f(x)=c\) і\(f(x+h)=c\), таким чином отримуємо наступний результат:
\[\begin{align*} f′(x) &=\lim_{h→0} \dfrac{f(x+h)−f(x)}{h} \\[4pt] &=\lim_{h→0}\dfrac{c−c}{h} \\[4pt] &=\lim_{h→0}\dfrac{0}{h} \\[4pt] &=\lim_{h→0}0=0. \end{align*}\]
Правило диференціації постійних функцій називається правилом константи. Він стверджує, що похідна постійної функції дорівнює нулю; тобто, оскільки постійна функція - це горизонтальна лінія, нахил або швидкість зміни постійної функції є\(0\). Ми повторюємо це правило в наступній теоремі.
Нехай\(c\) буде постійною. Якщо\(f(x)=c\), то\(f′(x)=0.\)
Крім того, ми можемо висловити це правило як
\[\dfrac{d}{dx}(c)=0. \nonumber \]
Знайдіть похідну від\(f(x)=8.\)
Рішення
Це всього лише одноетапне застосування правила:\(f′(8)=0.\)
Знайдіть похідну від\(g(x)=−3\).
- Підказка
-
Використовуйте попередній приклад як орієнтир
- Відповідь
-
0
Правило влади
Ми показали, що
\[\dfrac{d}{dx}\left(x^2\right)=2x\quad\text{ and }\quad\dfrac{d}{dx}\left(x^{1/2}\right)=\dfrac{1}{2}x^{−1/2}. \nonumber \]
На цьому етапі ви можете побачити шаблон, який починає розвиватися для похідних форми\(\dfrac{d}{dx}\left(x^n\right)\). Продовжуємо дослідження похідних формул шляхом диференціювання степеневих функцій виду\(f(x)=x^n\), де\(n\) є натуральне число. Розроблено формули для похідних цього типу функцій поетапно, починаючи з натуральних чисел. Перш ніж констатувати і доводити загальне правило для похідних функцій цієї форми, розглянемо конкретний випадок,\(\dfrac{d}{dx}(x^3)\). Коли ми проходимо через цю деривацію, зверніть особливу увагу на частину виразу жирним шрифтом, оскільки техніка, яка використовується в цьому випадку, по суті така ж, як і техніка, яка використовується для доведення загального випадку.
Знайти\(\dfrac{d}{dx}\left(x^3\right)\).
Рішення:
| \(\displaystyle \dfrac{d}{dx}\left(x^3\right)=\lim_{h→0}\dfrac{(x+h)^3−x^3}{h}\) | |
| \(\displaystyle =\lim_{h→0}\dfrac{x^3+3x^2h+3xh^2+h^3−x^3}{h}\) | Зверніть увагу, що перший термін у розширенні\((x+h)^3\) є,\(x^3\) а другий термін є\(3x^2h\). Усі інші терміни містять повноваження\(h\), які є двома або більшими. |
| \(\displaystyle =\lim_{h→0}\dfrac{3x^2h+3xh^2+h^3}{h}\) | На цьому кроці\(x^3\) умови були скасовані, залишивши лише терміни, що містять\(h\). |
| \(\displaystyle =\lim_{h→0}\dfrac{h(3x^2+3xh+h^2)}{h}\) | Фактор з загального фактора\(h\). |
| \(\displaystyle =\lim_{h→0}(3x^2+3xh+h^2)\) | Після скасування загального фактора\(h\), єдиним терміном, який не містить\(h\) є\(3x^2\). |
| \(=3x^2\) | \(h\)Відпустіть в\(0\). |
Знайти\(\dfrac{d}{dx}\left(x^4\right).\)
- Підказка
-
Використовуйте\((x+h)^4=x^4+4x^3h+6x^2h^2+4xh^3+h^4\) та дотримуйтесь процедури, описаної в попередньому прикладі.
- Відповідь
-
\(\dfrac{d}{dx}\left(x^4\right) = 4x^3\)
Як ми побачимо, процедура знаходження похідної загальної форми\(f(x)=x^n\) дуже схожа. Хоча часто нерозумно робити загальні висновки з конкретних прикладів, ми зауважимо\(f(x)=x^3\), що при диференціації потужність на\(x\) стає коефіцієнтом\(x^2\) в похідній, а потужність на\(x\) в похідній зменшується на 1. Наступна теорема стверджує, що правило влади має для всіх натуральних чисел степенів\(x\). Ми врешті-решт продовжимо цей результат до від'ємних цілих сил. Пізніше ми побачимо, що це правило також може бути поширене спочатку на раціональні повноваження,\(x\) а потім на довільні повноваження\(x\). Майте на увазі, однак, що це правило не поширюється на функції, в яких константа підвищується до змінної потужності, наприклад\(f(x)=3^x\).
\(n\)Дозволяти бути натуральним цілим числом. Якщо\(f(x)=x^n\), то
\[f′(x)=nx^{n−1}. \nonumber \]
Крім того, ми можемо висловити це правило як
\[\dfrac{d}{dx}\left(x^n\right)=nx^{n−1.} \nonumber \]
Для\(f(x)=x^n\) де\(n\) є натуральне число, у нас є
\[f′(x)=\lim_{h→0}\dfrac{(x+h)^n−x^n}{h}. \nonumber \]
Так як
\((x+h)^n=x^n+nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n,\)
ми бачимо, що
\((x+h)^n−x^n=nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n.\)
Далі розділіть обидві сторони на h:
\(\dfrac{(x+h)^n−x^n}{h}=\dfrac{nx^{n−1}h+\binom{n}{2}x^{n−2}h^2+\binom{n}{3}x^{n−3}h^3+…+nxh^{n−1}+h^n}{h}.\)
Таким чином,
\(\dfrac{(x+h)^n−x^n}{h}=nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n−1}.\)
Нарешті,
\[f′(x)=\lim_{h→0}(nx^{n−1}+\binom{n}{2}x^{n−2}h+\binom{n}{3}x^{n−3}h^2+…+nxh^{n−2}+h^{n-1}) \nonumber \]
\(=nx^{n−1}.\)
□
Знайдіть похідну функції\(f(x)=x^{10}\), застосувавши правило влади.
Рішення
Використовуючи правило харчування с\(n=10\), отримуємо
\[f'(x)=10x^{10−1}=10x^9. \nonumber \]
Знайдіть похідну від\(f(x)=x^7\).
- Підказка
-
Використовуйте правило живлення за допомогою\(n=7.\)
- Відповідь
-
\(f′(x)=7x^6\)
Сума, різниця та постійні множинні правила
Ми знаходимо наші наступні правила диференціації, розглядаючи похідні сум, відмінностей та постійних кратних функцій. Так само, як і коли ми працюємо з функціями, існують правила, які полегшують пошук похідних функцій, які ми додаємо, віднімаємо або множимо на константу. Ці правила узагальнені в наступній теоремі.
\(g(x)\)Дозволяти\(f(x)\) і бути диференційованими функціями і\(k\) бути постійною. Тоді кожне з наступних рівнянь тримає.
Правило суми. Похідна суми функції\(f\) і функції така ж, як сума похідної від\(f\) і похідної від\(g\).\(g\)
\[\dfrac{d}{dx}\big(f(x)+g(x)\big)=\dfrac{d}{dx}\big(f(x)\big)+\dfrac{d}{dx}\big(g(x)\big); \nonumber \]
тобто,
\[\text{for }s(x)=f(x)+g(x),\quad s′(x)=f′(x)+g′(x). \nonumber \]
Правило різниці. Похідна різниці функції\(f\) і функції така ж, як різниця похідної від\(f\) і похідної від\(g\):\(g\)
\[\dfrac{d}{dx}(f(x)−g(x))=\dfrac{d}{dx}(f(x))−\dfrac{d}{dx}(g(x)); \nonumber \]
тобто,
\[\text{for }d(x)=f(x)−g(x),\quad d′(x)=f′(x)−g′(x). \nonumber \]
Постійне множинне правило. Похідна константи,\(k\) помножена на функцію\(f\), така ж, як і константа, помножена на похідну:
\[\dfrac{d}{dx}\big(kf(x)\big)=k\dfrac{d}{dx}\big(f(x)\big); \nonumber \]
тобто,
\[\text{for }m(x)=kf(x),\quad m′(x)=kf′(x). \nonumber \]
Тут ми надаємо лише підтвердження правила суми. Решта слідують аналогічним чином.
Для диференційовних функцій\(f(x)\) і\(g(x)\), задаємо\(s(x)=f(x)+g(x)\). Використовуючи граничне визначення похідної, яку ми маємо
\[s′(x)=\lim_{h→0}\dfrac{s(x+h)−s(x)}{h}.\nonumber \]
Підставляючи\(s(x+h)=f(x+h)+g(x+h)\) і\(s(x)=f(x)+g(x),\) отримуємо
\[s′(x)=\lim_{h→0}\dfrac{\big(f(x+h)+g(x+h)\big)−\big(f(x)+g(x)\big)}{h}.\nonumber \]
Переставляючи і перегрупувати терміни, ми маємо
\[s′(x)=\lim_{h→0}\left(\dfrac{f(x+h)−f(x)}{h}+\dfrac{g(x+h)−g(x)}{h}\right).\nonumber \]
Тепер ми застосовуємо закон суми для лімітів та визначення похідної для отримання
\[s′(x)=\lim_{h→0}\dfrac{f(x+h)−f(x)}{h}+\lim_{h→0}\dfrac{g(x+h)−g(x)}{h}=f′(x)+g′(x).\nonumber \]
□
Знайдіть похідну від\(g(x)=3x^2\) і порівняйте її з похідною\(f(x)=x^2.\)
Рішення
Використовуємо безпосередньо правило харчування:
\[g′(x)=\dfrac{d}{dx}(3x^2)=3\dfrac{d}{dx}(x^2)=3(2x)=6x.\nonumber \]
Оскільки\(f(x)=x^2\) має похідну\(f′(x)=2x\), ми бачимо, що похідна в\(g(x)\) 3 рази більше похідної від\(f(x)\). Цей зв'язок проілюстровано на малюнку\(\PageIndex{1}\).
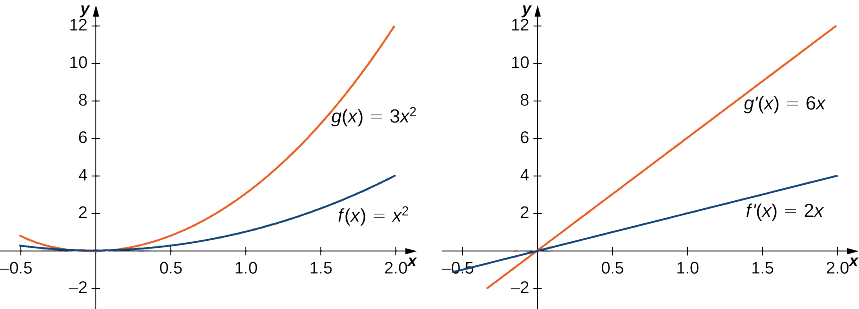
Знайдіть похідну від\(f(x)=2x^5+7\).
Рішення
Почнемо з застосування правила диференціації суми двох функцій, за яким слідують правила диференціації постійних кратних функцій і правило диференціації ступенів. Щоб краще зрозуміти послідовність, в якій застосовуються правила диференціації, використовуємо позначення Лейбніца по всьому розв'язку:
\ (\ почати {вирівнювати*} f′ (x) &=\ dfrac {d} {dx}\ ліворуч (2x^5+7\ праворуч)\\ [4pt]
&=\ dfrac {d} {dx} (2x^5) +\ dfrac {d} {dx} (7) &\ text {Застосувати правило суми.}\\ [4pt]
&=2\ dx frac {d} {dx} (x^5) +\ dfrac {d} {dx} (7) &\ text {Застосувати постійне кратне правило.}\\ [4pt]
&=2 (5 x^4) +0 &\ text {Застосувати правило живлення та правило константи.}\\ [4pt]
&=10x^4 &\ text {Спрощення.} \ end {вирівнювати*}\)
Знайдіть похідну від\(f(x)=2x^3−6x^2+3.\)
- Підказка
-
Використовуйте попередній приклад як орієнтир.
- Відповідь
-
\(f′(x)=6x^2−12x.\)
Знайти рівняння прямої дотичної до графіка\(f(x)=x^2−4x+6\) at\(x=1\)
Рішення
Щоб знайти рівняння дотичної прямої, нам знадобиться точка і ухил. Щоб знайти точку, обчислити
\[f(1)=1^2−4(1)+6=3. \nonumber \]
Це дає нам крапку\((1,3)\). Так як нахил дотичної лінії в 1 є\(f′(1)\), ми повинні спочатку знайти\(f′(x)\). Використовуючи визначення похідної, ми маємо
\[f′(x)=2x−4\nonumber \]
так нахил дотичної лінії є\(f′(1)=−2\). Використовуючи формулу точка-нахил, бачимо, що рівняння дотичної прямої
\[y−3=−2(x−1).\nonumber \]
Поставивши рівняння прямої в ухило-перехопленому вигляді, отримаємо
\[y=−2x+5.\nonumber \]
Знайти рівняння прямої дотичної до графіка\(f(x)=3x^2−11\) at\(x=2\). Використовуйте точково-ухил форму.
- Підказка
-
Використовуйте попередній приклад як орієнтир.
- Відповідь
-
\(y=12x−23\)
Правило продукту
Тепер, коли ми розглянули основні правила, ми можемо почати розглядати деякі з більш просунутих правил. Перший досліджує похідну добутку двох функцій. Хоча може бути спокусливо припустити, що похідна продукту є добутком похідних, подібно до правил суми та різниці, правило продукту не відповідає цій схемі. Щоб зрозуміти, чому ми не можемо використовувати цей шаблон, розглянемо функцію\(f(x)=x^2\), похідна якої є,\(f′(x)=2x\) а ні\(\dfrac{d}{dx}(x)⋅\dfrac{d}{dx}(x)=1⋅1=1.\)
\(g(x)\)Дозволяти\(f(x)\) і бути диференційованими функціями. Тоді
\[\dfrac{d}{dx}(f(x)g(x))=\dfrac{d}{dx}(f(x))⋅g(x)+\dfrac{d}{dx}(g(x))⋅f(x). \nonumber \]
Тобто,
\[\text{if }p(x)=f(x)g(x),\quad \text{then }p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
Це означає, що похідна добутку двох функцій є похідною першої функції, що умножує другу функцію плюс похідна другої функції на першу функцію.
Почнемо з припущення, що\(f(x)\) і\(g(x)\) є диференційованими функціями. У ключовий момент цього доказу нам потрібно використовувати той факт, що, оскільки\(g(x)\) диференційований, він також є безперервним. Зокрема, ми використовуємо той факт, що оскільки\(g(x)\) є безперервним,\(\displaystyle \lim_{h→0}g(x+h)=g(x).\)
Застосовуючи граничне визначення похідної до\(p(x)=f(x)g(x),\) отримуємо
\[ p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Додаючи і віднімаючи\(f(x)g(x+h)\) в чисельнику, ми маємо
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)+f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Після розбивання цього частки і застосування закону суми для лімітів похідна стає
\[p′(x)=\lim_{h→0}\dfrac{f(x+h)g(x+h)−f(x)g(x+h)}{h}+\lim_{h→0}\dfrac{f(x)g(x+h)−f(x)g(x)}{h}.\nonumber \]
Переставляючи, отримуємо
\ [\ почати {вирівнювати*} p′ (x) &=\ lim_ {h → 0}\ ліворуч (\ dfrac {f (x+h) −f (x)} {h} ⋅г (x+h)\ праворуч) +\ lim_ {h → 0}\ ліворуч (\ dfrac {g (x+h) −g (x)} {h} праворуч)\\ [4pt]
&=\ ліворуч (\ lim_ {h→0}\ dfrac {f (x+h) −f (x)} {h}\ праворуч) ⋅\ ліворуч (\ lim_ {h→0}\; g (x+h)\ праворуч) +\ ліворуч (\ lim_ {h → 0}\ dfrac {г (x+h)\ праворуч) +\ ліворуч (\ lim_ {h → 0}\ dfrac {g (x+h) −г (х))} {h}\ праворуч) ⋅f (x)\ end {align*}\]
Використовуючи безперервність\(g(x)\), визначення похідних\(f(x)\) і\(g(x)\), і застосовуючи граничні закони, ми приходимо до правила продукту,
\[p′(x)=f′(x)g(x)+g′(x)f(x).\nonumber \]
□
Для\(p(x)=f(x)g(x)\), скористайтеся правилом продукту, щоб знайти\(f(2)=3,\; f′(2)=−4,\; g(2)=1\),\(p′(2)\) якщо, і\(g′(2)=6\).
Рішення
Так як\(p(x)=f(x)g(x)\),\(p′(x)=f′(x)g(x)+g′(x)f(x),\) а значить
\(p′(2)=f′(2)g(2)+g′(2)f(2)=(−4)(1)+(6)(3)=14.\)
Для\(p(x)=(x^2+2)(3x^3−5x),\) пошуку\(p′(x)\) можна застосувати правило продукту. Перевірте результат, спочатку знайшовши продукт, а потім диференціювавши.
Рішення
Якщо ставимо\(f(x)=x^2+2\) і\(g(x)=3x^3−5x\), то\(f′(x)=2x\) і\(g′(x)=9x^2−5\). Таким чином,
\(p′(x)=f′(x)g(x)+g′(x)f(x)=(2x)(3x^3−5x)+(9x^2−5)(x^2+2).\)
Спрощуючи, ми маємо
\[p′(x)=15x^4+3x^2−10. \nonumber \]
Щоб перевірити, ми бачимо, що\(p(x)=3x^5+x^3−10x\) і, отже,\(p′(x)=15x^4+3x^2−10.\)
Використовуйте правило продукту, щоб отримати похідну\(p(x)=2x^5(4x^2+x).\)
- Підказка
-
Встановіть\(f(x)=2x^5\)\(g(x)=4x^2+x\) і використовуйте попередній приклад як орієнтир.
- Відповідь
-
\(p′(x)=10x^4(4x^2+x)+(8x+1)(2x^5)=56x^6+12x^5.\)
Правило частки
Розробивши і відпрацювавши правило продукту, ми тепер розглянемо диференціювання коефіцієнтів функцій. Як ми бачимо в наступній теоремі, похідна частки не є часткою похідних; скоріше, це похідна функції в чисельнику разів функція в знаменнику мінус похідна функції в знаменнику рази похідна функції в знаменнику раз функція в чисельнику, все ділиться на квадрат функції в знаменнику. Для того, щоб краще зрозуміти, чому ми не можемо просто взяти частку похідних, майте на увазі, що
\[\dfrac{d}{dx}(x^2)=2x,\text{ not }\dfrac{\dfrac{d}{dx}(x^3)}{\dfrac{d}{dx}(x)}=\dfrac{3x^2}{1}=3x^2.\nonumber \]
\(g(x)\)Дозволяти\(f(x)\) і бути диференційованими функціями. Тоді
\[\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{\dfrac{d}{dx}(f(x))⋅g(x)−\dfrac{d}{dx}(g(x))⋅f(x)}{\big(g(x)\big)^2}. \nonumber \]
Тобто, якщо
\[q(x)=\dfrac{f(x)}{g(x)}\nonumber \]
потім
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}.\nonumber \]
Доказ правила частки дуже схожий на доказ правила продукту, тому воно тут опущено. Замість цього ми застосовуємо це нове правило для пошуку похідних у наступному прикладі.
Використовуйте часткове правило, щоб знайти похідну від\(q(x)=\dfrac{5x^2}{4x+3}.\)
Рішення
Нехай\(f(x)=5x^2\) і\(g(x)=4x+3\). Таким чином,\(f′(x)=10x\) і\(g′(x)=4\).
Підставляючи в часткове правило, ми маємо
\[q′(x)=\dfrac{f′(x)g(x)−g′(x)f(x)}{(g(x))^2}=\dfrac{10x(4x+3)−4(5x^2)}{(4x+3)^2}.\nonumber \]
Спрощуючи, отримуємо
\[q′(x)=\dfrac{20x^2+30x}{(4x+3)^2}\nonumber \]
Знайдіть похідну від\(h(x)=\dfrac{3x+1}{4x−3}\).
- Підказка
-
Застосовуйте часткове правило з\(f(x)=3x+1\) і\(g(x)=4x−3\).
- Відповідь
-
\(h′(x)=−\dfrac{13}{(4x−3)^2}.\)
Тепер можна використовувати часткове правило для розширення правила влади, щоб знайти похідні функцій виду,\(x^k\) де\(k\) є від'ємне ціле число.
Якщо\(k\) від'ємне ціле число, то
\[\dfrac{d}{dx}(x^k)=kx^{k−1}. \nonumber \]
Якщо\(k\) від'ємне ціле число, ми можемо встановити\(n=−k\), так що п - натуральне число з\(k=−n\). Оскільки для кожного натурального цілого числа\(n\)\(x^{−n}=\dfrac{1}{x^n}\), ми можемо тепер застосувати часткове правило, встановивши\(f(x)=1\) і\(g(x)=x^n\). В даному випадку\(f′(x)=0\) і\(g′(x)=nx^{n−1}\). Таким чином,
\[\dfrac{d}{dx}(x^{−n})=\dfrac{0(x^n)−1(nx^{n−1})}{(x^n)^2}.\nonumber \]
Спрощуючи, ми бачимо, що
\[\begin{align*} \dfrac{d}{dx}(x^{−n}) &=\dfrac{−nx^{n−1}}{x^{2n}}\\[4pt]&=−nx^{(n−1)−2n}\\[4pt]&=−nx^{−n−1}.\end{align*}\]
Нарешті, зауважте, що оскільки\(k=−n\), підставляючи ми маємо
\[\dfrac{d}{dx}(x^k)=kx^{k−1}.\nonumber \]
□
Знайти\(\dfrac{d}{dx}(x^{−4})\).
Рішення
Застосовуючи розширене правило потужності с\(k=−4\), отримуємо
\[\dfrac{d}{dx}(x^{−4})=−4x^{−4−1}=−4x^{−5}.\nonumber \]
Використовуйте розширене правило живлення та постійне множинне правило, щоб знайти\(f(x)=\dfrac{6}{x^2}\).
Рішення
Може здатися спокусливим використовувати часткове правило, щоб знайти цю похідну, і це, звичайно, не було б неправильним. Однак набагато простіше диференціювати цю функцію, попередньо переписавши її як\(f(x)=6x^{−2}\).
\ (\ почати {align*} f′ (x) &=\ dfrac {d} {dx}\ ліворуч (\ dfrac {6} {x^2}\ праворуч) =\ dfrac {d} {dx}\ ліворуч (6x^ {−2}\ праворуч) &\ текст {переписати}\ dfrac {6} {x^2}\ текст {як} 6x2} ^ {−2}.\\ [4pt]
&=6\ dfrac {d} {dx}\ ліворуч (x^ {−2}\ праворуч) &\ text {Застосувати постійне кратне правило.}\\ [4pt]
&=6 (−2x^ { −3}) &\ text {Використовуйте розширене правило живлення для диференціації} x^ {−2}.\\ [4pt]
&=−12x^ {−3} &\ text {Simplify.} \ end {вирівнювати*}\)
Знайдіть похідну від\(g(x)=\dfrac{1}{x^7}\) використання правила розширеної потужності.
- Підказка
-
Перепишіть\(g(x)=\dfrac{1}{x^7}=x^{−7}\). Використовуйте розширене правило живлення з\(k=−7\).
- Відповідь
-
\(g′(x)=−7x^{−8}\).
Поєднання правил диференціації
Як ми бачили на прикладах у цьому розділі, рідко трапляється, що ми закликаємо застосувати лише одне правило диференціації, щоб знайти похідну заданої функції. На цьому етапі, поєднуючи правила диференціації, ми можемо знайти похідні будь-якої поліноміальної або раціональної функції. Пізніше ми зіткнемося з більш складними комбінаціями правил диференціації. Хорошим правилом для використання при застосуванні декількох правил є застосування правил у зворотному порядку, в якому ми б оцінили функцію.
Для\(k(x)=3h(x)+x^2g(x)\), знайдіть\(k′(x)\).
Рішення: Для пошуку цієї похідної потрібно правило суми, постійне кратне правило та правило добутку.
| \(k′(x)=\dfrac{d}{dx}\big(3h(x)+x^2g(x)\big)=\dfrac{d}{dx}\big(3h(x)\big)+\dfrac{d}{dx}\big(x^2g(x)\big)\) | Застосуйте правило суми. |
| \(=3\dfrac{d}{dx}\big(h(x)\big)+\left(\dfrac{d}{dx}(x^2)g(x)+\dfrac{d}{dx}(g(x))x^2\right)\) | Застосовуйте постійне множинне правило для диференціації\(3h(x)\) та правило продукту для диференціації\(x^2g(x)\). |
| \(=3h′(x)+2xg(x)+g′(x)x^2\) |
Для\(k(x)=f(x)g(x)h(x)\), висловити\(k′(x)\) в терміні\(f(x),g(x),h(x)\), і їх похідні.
Рішення
Ми можемо думати про функцію\(k(x)\) як добуток функції\(f(x)g(x)\) і функції\(h(x)\). Тобто,\(k(x)=(f(x)g(x))⋅h(x)\). Таким чином,
\ (\ почати {align*} k′ (x) &=\ dfrac {d} {dx}\ великий (f (x) g (x)\ великий) ⋅h (x) +\ dfrac {d} {dx}\ великий (h (x)\ великий (f (x) g (x)\ великий). &\ text {Застосувати правило продукту до добутку} f (x) g (x)\ text {і} h (x).\\ [4pt]
&=\ великий (f′ (x) g (x) +g′ (x) f (x)\ big) h (x) +h ′ (x) f (x) g (x) &\ text {Застосувати правило продукту} f (x) г (х)\\ [4pt]
&= f′ (х) г (х) год (х) +f (x) g′ (x) h (x) +f (x) г (х) h (x). &\ текст {Спрощення.} \ end {вирівнювати*}\)
Для\(h(x)=\dfrac{2x^3k(x)}{3x+2}\), знайдіть\(h′(x)\).
Рішення
Ця процедура характерна для знаходження похідної від раціональної функції.
\ (\ begin {align*} h′ (x) &=\ dfrac {\ dfrac {d} {dx} (2x^3k (x)) ⋅ (3x+2) −\ dfrac {d} {dx} (3x+2) ⋅ (2x^3k (x))} {(3x+2) ^2} &\ text {Застосувати правило частки}.\\ [4pt]
&=\ dfrac {(6x^2k (x) +k′ (x) ⋅2x^3) (3x+2) −3 (2x^3k (x))} {(3x+2) ^2} &\ text {Застосуйте правило продукту, щоб знайти}\ dfrac {d} {dx} (2x^3k (x)). \ текст {Використовувати}\ dfrac {d} {dx} (3x+2) =3.\\ [4pt]
&=\ dfrac {−6x^3k (x) +12х^2k (x) +6х^4kk (x) +4x^3k′ (x)} {(3x+2) ^2} &\ текст {Спростити}\ end {align*}\)
Знайти\(\dfrac{d}{dx}(3f(x)−2g(x)).\)
- Підказка
-
Застосуйте правило різниці та постійне множинне правило.
- Відповідь
-
\(3f′(x)−2g′(x).\)
Визначте значення\(x\) для яких\(f(x)=x^3−7x^2+8x+1\) має горизонтальна дотична лінія.
Рішення
Щоб знайти значення\(x\) для яких\(f(x)\) має горизонтальна дотична лінія, ми повинні вирішити\(f′(x)=0\).
З тих пір\(f′(x)=3x^2−14x+8=(3x−2)(x−4)\),
ми повинні вирішити\((3x−2)(x−4)=0\). Таким чином, ми бачимо, що функція має горизонтальні дотичні лінії в\(x=\dfrac{2}{3}\) і\(x=4\), як показано на наступному графіку.
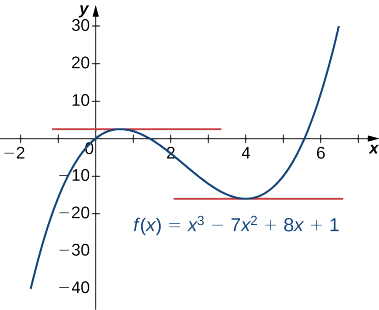
Положення об'єкта на осі координат в часі\(t\) задається\(s(t)=\dfrac{t}{t^2+1}.\) Якою початковою швидкістю об'єкта?
Рішення
Оскільки початкова швидкість\(v(0)=s′(0),\) починається з знаходження\(s′(t)\), застосовуючи часткове правило:
\(s′(t)=\dfrac{1(t^2+1)−2t(t)}{(t^2+1)^2}=\dfrac{1−t^2}{(t^2+1)^2}\).
Оцінивши, ми бачимо, що\(v(0)=1.\)
Знайти значення,\(x\) для яких дотична до графіка прямої\(f(x)=4x^2−3x+2\) має дотичну пряму, паралельну прямій.\(y=2x+3.\)
- Підказка
-
Вирішити\(f′(x)=2\).
- Відповідь
-
\(\dfrac{5}{8}\)
Автомобільні перегони Формули-1 можуть бути дуже захоплюючими для перегляду та залучення великої кількості глядачів. Дизайнери треків Формули-1 повинні забезпечити достатній простір трибуни навколо доріжки, щоб розмістити цих глядачів. Однак автомобільні перегони можуть бути небезпечними, а міркування безпеки є першорядними. Трибуни повинні бути розміщені там, де глядачам не загрожує небезпека, якщо водій втратить контроль над автомобілем (рис.\(\PageIndex{3}\)).

Безпека особливо турбує на поворотах. Якщо водій недостатньо гальмує перед входом в поворот, автомобіль може зісковзнути з іподрому. Зазвичай це просто призводить до більш широкого повороту, який уповільнює водія. Але якщо водій втратить управління повністю, автомобіль може злетіти з траси цілком, по дотичній до кривої траси іподрому.
Припустимо, ви проектуєте новий трек Формули-1. Одна ділянка доріжки може бути змодельована функцією\(f(x)=x^3+3x^2+x\) (рис.\(\PageIndex{4}\)). Поточний план передбачає, що трибуни будуть побудовані вздовж першої одразу та навколо частини першої кривої. Плани передбачають, що передній кут трибуни повинен бути розташований у точці (\(−1.9,2.8\)). Ми хочемо визначити, чи загрожує ця локація глядачам, якщо водій втратить контроль над автомобілем.
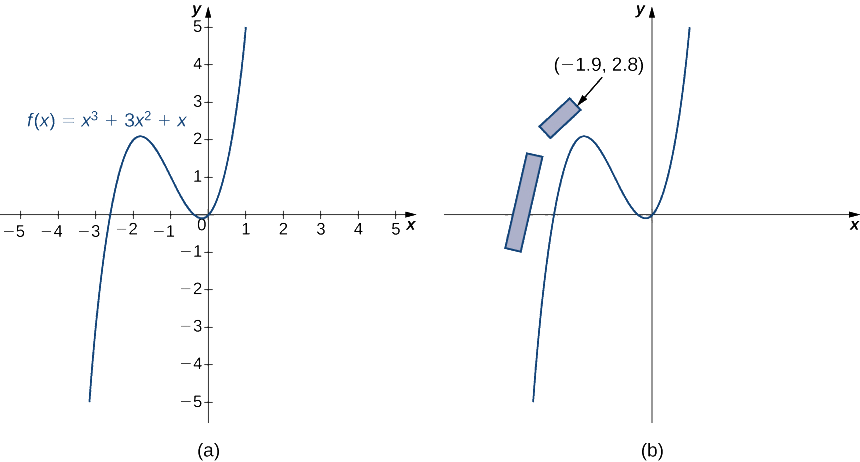
- Фізики визначили, що водії, швидше за все, втратять контроль над своїми автомобілями, коли вони йдуть в поворот, в точці, де нахил дотичної лінії дорівнює 1. Знайдіть\((x,y)\) координати цієї точки біля повороту.
- Знайдіть рівняння дотичної лінії до кривої в цій точці.
- Щоб визначити, чи загрожує глядачам небезпека в цьому сценарії, знайдіть\(x\) -координату точки, де дотична лінія перетинає лінію\(y=2.8\). Чи безпечно цей пункт праворуч від трибуни? Або глядачам загрожує небезпека?
- Що робити, якщо водій втрачає контроль раніше, ніж проект фізиків? Припустимо, водій втрачає контроль у точці (\(−2.5,0.625\)). Який нахил дотичної лінії в цій точці?
- Якщо водій втрачає контроль, як описано в частині 4, чи безпечні глядачі?
- Чи варто продовжувати поточний дизайн трибуни, або трибуни повинні бути переміщені?
Ключові концепції
- Похідна постійної функції дорівнює нулю.
- Похідна від степеневої функції - це функція, при якій влада включена\(x\) стає коефіцієнтом члена, а влада включена\(x\) в похідній зменшується на 1.
- Похідна константи,\(c\) помножена на функцію\(f\), така ж, як і константа, помножена на похідну.
- Похідна суми функції\(f\) і функції така ж, як сума похідної від\(f\) і похідної від\(g\).\(g\)
- Похідна різниці функції\(f\) і функції така ж, як різниця похідної від\(f\) і похідної від\(g\).\(g\)
- Похідна добутку двох функцій є похідною першої функції, що умножує другу функцію плюс похідна другої функції на першу функцію.
- Похідна частки двох функцій є похідною першої функції на другу за вирахуванням похідної другої функції на першу функцію, розділену на квадрат другої функції.
- Ми використовували граничне визначення похідної для розробки формул, що дозволяють знаходити похідні, не вдаючись до визначення похідної. Ці формули можна використовувати поодинці або в поєднанні один з одним.
Глосарій
- постійне множинне правило
- похідна константи,\(c\) помноженої на функцію,\(f\) така ж, як і константа, помножена на похідну:\(\dfrac{d}{dx}\big(cf(x)\big)=cf′(x)\)
- постійне правило
- похідна постійної функції дорівнює нулю:\(\dfrac{d}{dx}(c)=0\), де\(c\) константа
- різниця правило
- похідна різниці функції\(f\) і функції така ж, як різниця похідної від\(f\) і похідної від\(g\):\(g\)\(\dfrac{d}{dx}\big(f(x)−g(x)\big)=f′(x)−g′(x)\)
- влада правило
- похідна від степеневої функції - це функція, в якій влада включена\(x\) стає коефіцієнтом члена, а влада включена\(x\) в похідній зменшується на 1: Якщо\(n\) ціле число, то\(\dfrac{d}{dx}\left(x^n\right)=nx^{n−1}\)
- правило продукту
- похідна добутку двох функцій є похідною першої функції, що умножує другу функцію плюс похідна другої функції на першу функцію:\(\dfrac{d}{dx}\big(f(x)g(x)\big)=f′(x)g(x)+g′(x)f(x)\)
- частка правило
- похідна частки двох функцій є похідною першої функції на другу за вирахуванням похідної другої функції на першу функцію, розділену на квадрат другої функції:\(\dfrac{d}{dx}\left(\dfrac{f(x)}{g(x)}\right)=\dfrac{f′(x)g(x)−g′(x)f(x)}{\big(g(x)\big)^2}\)
- сума правило
- похідна суми функції\(f\) і функції така ж, як сума похідної від\(f\) і похідної від\(g\):\(g\)\(\dfrac{d}{dx}\big(f(x)+g(x)\big)=f′(x)+g′(x)\)
