13.1: Перешкоди

Подвійна щілина

Класичне розташування експерименту з подвійною щілиною проілюстровано на рис\( 13.1\). Є непрозорий екран з двома вузькими прорізами в ньому в\(z = 0\) площині (показаний в поперечному перерізі в\(x-z\) площині — щілини виходять з паперу в\(y\) напрямку) на невеликій\(s\) відстані один від одного. Непрозорий екран висвітлюється «точковим» джерелом світла. Наприклад, це може бути світло з прозорою скляною колбою та кольоровим фільтром, щоб вибрати вузький діапазон частот, далеко в\(z\) напрямку −. Лазерний промінь, розкинутий лінзою, буде служити так само добре. Важливо - виробляти освітлення на непрозорому екрані, в якому частота знаходиться у вузькому діапазоні, а фаза світла, що досягає двох щілин, корелюється. Це, безумовно, буде вірно, якщо освітленість для\(z < 0\) майже плоска хвиля.

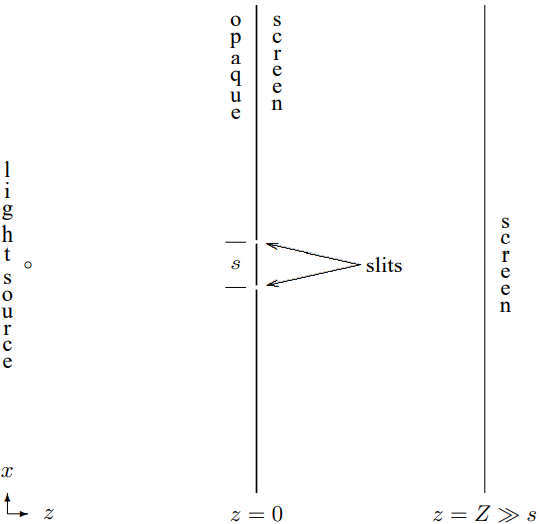
Малюнок\( 13.1\): Експеримент з подвійною щілиною.

Тепер цікава річ відбувається на другому екрані, в\(z = Z\). Цей «екран» може бути фотографічною пластинкою, напівпрозорим екраном або навіть вашою сітківкою. Що з'являється на цьому екрані - це серія паралельних ліній яскравості в\(y\) напрямку (паралельно щілинам). Якщо одна з щілин прикрита, лінії зникають.

Те, що відбувається, - це перешкоди між двома можливими прямими шляхами, за допомогою яких світло може досягати екрана. Ми дамо евристичне, фізичне обговорення втручання в цьому розділі. Тоді в наступному розділі ми отримаємо той самий результат, використовуючи вид примусових коливань та аргументів граничних умов, які ви знаєте з нашого дослідження одновимірних хвиль.

Фізична картина така. Електричне поле при\(z = Z\) - це сума полів, що надходять з двох щілин. При\(x = 0\), в симетричному розташуванні\( 13.1\), показаному на малюнку, два можливих шляху для світла мають однакову довжину. Тому дві складові поля мають однакову фазу. Тому вони заважають «конструктивно» і йде яскрава лінія при\(x = 0\). У міру зміни x\(z = Z\), при зміні відносної довжини двох шляхів змінюється. Потім ми отримаємо чергування позицій конструктивного та руйнівного втручання. Це породжує яскраві лінії.

Ми можемо зрозуміти ефект кількісно, обчислюючи довжину шляху явно. Розглянемо точку на екрані в\(x = X\). Це показано на малюнку\( 13.2\).

Довжина пунктирної лінії на малюнку\( 13.2\) дорівнює\[\sqrt{X^{2}+Z^{2}}.\]

Для верхньої і нижньої щілин довжини шляху трохи коротше і довше відповідно. Загальна різниця в довжині шляху\[\Delta \ell=\sqrt{(X+s / 2)^{2}+Z^{2}}-\sqrt{(X-s / 2)^{2}+Z^{2}}.\]

Для\(Z \gg s\), ми можемо розширити\(\Delta \ell\) в (13.2) в серії Тейлора,\ [\ Delta\ ell\ приблизно\ frac {s X} {\ sqrt {X^ {2} +Z^ {2}}}.\)

Малюнок\( 13.2\): Довжини шляху.

Тому, якщо число кутових хвиль світла є\(k\), різниця фаз між двома шляхами\[\frac{k s X}{\sqrt{X^{2}+Z^{2}}}.\]

Ми отримуємо максимальну інтенсивність кожного разу, коли фаза кратна\(2 \pi\), коли\[\frac{k s X}{\sqrt{X^{2}+Z^{2}}}=2 n \pi\]

З точки зору довжини хвилі\(\lambda=2 \pi / k\), це\[\frac{X}{\sqrt{X^{2}+Z^{2}}}=n \frac{\lambda}{s}.\]

Оптика Фур'є

Припустимо, що замість простого візерунка з двох прорізів на непрозорому екрані є якийсь більш складний малюнок. Загалом, хвильове збудження в\(z = 0\) площині ми можемо описати деякою функцією\(x\) і\(y,^{1}\)\[f(x, y).\]

Наша стратегія полягатиме в тому, щоб думати про хвилю, вироблену\(z > 0\) цією загальною функцією, як про суму ефектів крихітних дірок на всіх значеннях\(x\) і\(y\) для яких\(f(x, y)\) є ненульовими. Для кожного маленького фрагмента функції, ми можемо обчислити довжину шляху до певної точки на екрані в\(z = Z\). Потім ми можемо скласти всі шматочки.

Припустимо, для простоти,\(f(x, y)\) тобто тільки ненульовий в якомусь невеликому регіоні навколо походження, так що\(x\) і\(y\) буде мало\[x, y \ll Z\]

для всіх відповідних значень\(x\) і\(y\). Тепер довжина шляху від точки\((x, y, 0)\) на екрані\(z = 0\) в точці\((X, Y,Z)\) на екрані\(z = Z\) в\[\sqrt{(X-x)^{2}+(Y-y)^{2}+Z^{2}}.\]

Використовуючи (13.8), ми можемо розширити це наступним чином:\[R+\Delta \ell(x, y)+\cdots ,\]

де\[R=\sqrt{X^{2}+Y^{2}+Z^{2}}\]

і\[\Delta \ell(x, y)=-\frac{x X+y Y}{R}\]

Таким чином, хвиля на шляху від\((x, y, 0)\) до\((X, Y,Z)\) отримує фазу приблизно\[e^{i k(R+\Delta \ell)}.\]

Тепер ми можемо скласти шматки хвилі назад, щоб побачити, як працює перешкода в точці\((X, Y,Z)\). Ми просто підсумовуємо над усіма значеннями\(x\) і\(y\), з коефіцієнтом фази і функції,\(f(x, y)\). Тому що\(x\) і\(y\) є безперервними змінними, сума насправді є інтегралом,\[\int d x \int d y f(x, y) e^{i k(R+\Delta \ell)}=e^{i k R} \int d x \int d y f(x, y) e^{-i(x X+y Y) k / R}.\]

Як ми побачимо більш детально нижче, це двовимірне перетворення Фур'є функції,\(f(x, y)\).

Рівняння (13.14) є основним результатом оптики Фур'є. У ньому міститься значна частина фізики дифракції. Ми зробили ряд припущень, виводячи його, які потребують подальшого обговорення. У наступному розділі ми виведемо його по-іншому, розглядаючи хвилю для\(z > 0\) як результат вимушеного коливання, виробленого хвилею в\(z = 0\) площині. Це дасть нам альтернативний фізичний опис дифракції. Але буде корисно тримати на увазі просту картину складання всіх можливих шляхів, коли ми заглиблюємося в явища інтерференції та дифракції.

_____________________________

¹ Ми ігноруємо поляризацію.