1.8: Диференціальна форма закону Снелла

Закон Снелла у формі\(n \sin \theta\) = константа корисний для обчислення того, як промінь світла зігнутий при переході від одного середовища до іншого, де відбувається дискретна зміна показника заломлення. Якщо є середовище, в якій показник заломлення постійно змінюється, може стати в нагоді диференціальна форма закону Снелла. Це виходить просто диференціацією\(n \sin \theta\) = постійної, щоб отримати диференціальну форму закону Снелла

\[ \cot \theta d \theta = -\frac{dn}{n}.\label{eq:1.9.1} \]

Якщо висловити це через взаємодоповнюючий кут\(\Psi\) (див. Рис. I.24), це рівняння набуває вигляду

\[ \tan\Psi d \Psi = \frac{dn}{n}.\label{eq:1.9.2} \]

Давайте подивимося, як це може бути використано. Припустимо, наприклад, що у нас є якесь середовище, в якому показник заломлення зменшується лінійно з\(y\) координатою відповідно до

\[ n = n_0 - \frac{(n_0-1)y}{a}. \label{eq:1.9.3} \]

Цю форму має\(n = n_0\) при\(y = 0\), зменшуючись лінійно до\(n = 1\) ат\(y = a\). Ми вважаємо, що\(n = 1\) скрізь за межами\(y = a\). Рівняння спрощується, якщо ми запишемо\(\mu\) for\(n −1\) і\(\mu_0\) for\(n_0 −1\), так що

\[ \mu = \mu_0 \left(1 - \frac{y}{a}\right),\label{eq:1.9.4} \]

який має лінійно\(\mu\)\(\mu_0\) зменшуватися від нуля. Припустимо, що ми направляємо світловий промінь вгору від початку в напрямку, що робить кут\(\alpha\) з горизонталлю, і ми хочемо простежити промінь через середовище, коли показник заломлення постійно змінюється. Див. Малюнок I.24. Зі зміною показника заломлення, як у рівнянні\(\ref{eq:1.9.4}\), закон Снелла набуває вигляду

\[ tan \Psi d\Psi = -\frac{dy}{k-y}, \quad \text{where} \quad k = \frac{n_0a}{\mu_0}.\label{eq:1.9.5} \]

На інтеграції це стає

\[ y = k\left(1- \frac{\cos\alpha}{\cos\Psi}\right) \quad \text{or} \quad \cos\Psi = \frac{k\cos\alpha}{k-y}.\label{eq:1.9.6} \]

Це\((y, \Psi)\) рівняння шляху, пройденого світлом. З цього рівняння видно, що шлях стає горизонтальним, коли\(y = k(1 − \cos\alpha\). Щоб знайти\((x ,y)\) рівняння, використовуємо тотожності\( \cos\Psi = (1+\tan^2 \Psi)^{-1/2} \) і\( \tan\Psi =\frac{dy}{dx} \). Заміна їх у Рівняння\(\ref{eq:1.9.6}\) дає диференціальне рівняння шляху в\((x , y)\) координатах:

\[ \left(\frac{dy}{dx}\right)^2 = \frac{(k-y)^2 -l^2}{l^2}, \quad \text{where} \quad l = k\cos\alpha. \label{eq:1.9.10} \]

Це можна легко інтегрувати, щоб дати\((x ,y)\) рівняння шляху:

\[ x = l\ln\left[\frac{k(1+\sin\alpha)}{k-y\pm\sqrt{(k-y)^2-l^2}}\right]. \label{eq:1.9.11} \]

На малюнку I.25 я взяв\(a = 1\) (іншими словами, я висловлюю всі відстані в одиницях\(a\)), і я беру\(n_0 = 1.5\) (отже\(k = 3\)), і обчислюю шляхи для\(\alpha\) = 15°, 30°, 45°, 60°, 75°.

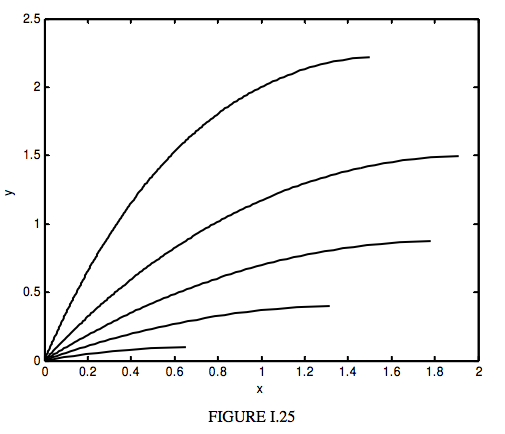
Рисунок I.25 та Рівняння\(\ref{eq:1.9.11}\) показують шляхи світла, якщо показник заломлення змінюється від\(n_0\) at\(y = 0\), до 1 at,\(y = a\) як описано рівнянням\(\ref{eq:1.9.3}\). Але тепер припустимо, що показник заломлення змінюється з висотою відповідно до

\[ n = \frac{n_0a}{(n_0-1)y+a}.\label{eq:1.9.12} \]

У цій моделі теж показник заломлення йде від\(n_0\) at\(y = 0\), до 1 at\(y = a\), але варіація не лінійна. Насправді ви можете переконати себе, що саме швидкість світла зростає лінійно від\(y = 0\) до\(y = a\). Подивіться, чи зможете ви простежити шляхи світлових променів в цій ситуації. Я думаю, що це дуги кіл, і ви можете обчислити радіуси і координати центрів кіл. Ось ще один:

\[ n = \sqrt{\frac{n^2_0a}{(n^2_0-1)y+a}}. \label{eq:1.9.13} \]

Тут теж показник заломлення йде від\(n_0\) ат\(y = 0\), до 1 ат\(y = a\). Ви можете спробувати простежити промені в цій моделі. Я думаю, що вони можуть бути дугами циклоїдів. Звичайно, ці приклади можуть здатися дуже малоймовірними. Чи можете ви уявити скляний блок ширини\(a\), виготовлений зі скла, показник заломлення якого безперервно змінюється від 1,5 на одному краю до нуля на іншому? Не дуже ймовірно, все ж є ситуація, яка спадає на думку, при якій відбувається безперервне зміна показника заломлення від якогось базального значення\(n_0\) до нуля. Я думаю про атмосферу Землі (або навіть про атмосферу будь-якої планети). Коли світло від зірки подорожує по атмосфері Землі, воно рухається не по прямій лінії, а в невеликій кривій, так що він відхиляється через кілька дугових хвилин до того, як він досягне телескопа астронома. Для зірки низько внизу біля горизонту заломлення становить майже половину градуса. Це потрібно враховувати, коли астрономи роблять точні позиційні вимірювання. А звукові хвилі, проходячи через атмосферу, також схильні до заломлення через диференціальну форму закону Снелла. Швидкість звуку (а значить і показник заломлення) змінюється в залежності від температури атмосфери, а значить, і з висотою в атмосфері. Серед багатьох застосувань такого роду теорії є шлях звукових хвиль від метеоритів, що мчать через атмосферу. Про це йдеться у статті, опублікованій в Метеоритика та планетарна наука 34, 572-585 (1999).