1.3: Заломлення на площинній поверхні

Коли промінь світла потрапляє в більш щільне середовище, він заломлюється до норми таким чином, ніж відношення синуса кута падіння до синуса кута заломлення є постійним, ця константа називається показником заломлення $n$.

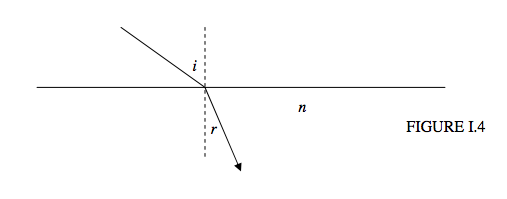
Це все гаразд, наскільки це йде, але ми можемо зробити краще.

1. Згадайте курмуджєтільки професора, який дасть вам лише половину оцінок, якщо ви також не скажете, що падаючий промінь, заломлений промінь і нормальний є компланарними.
2. рівняння

$$\dfrac{ \sin i }{ \sin r } = n, \label{eq:1.3.1}$$

де$n$ показник заломлення середовища, все в порядку до тих пір, поки світло потрапляє в середовище з вакууму. Показник заломлення повітря дуже мало відрізняється від одиниці. Детально про показник заломлення повітря можна знайти в розділі 7.1 Зоряних атмосфер і Розділі 11.3.3 Небесної механіки. Якщо світло рухається від одного середовища до іншого, закон заломлення набуває вигляду

$$n_1 \sin \theta_1 = n_2 \sin \theta_2. \label{eq:1.3.2}$$

iii. Заява закону Снелла, як зазначено вище, передбачає, якщо приймати буквально, що між показником заломлення та щільністю існує відношення один до одного. Повинна бути формула, що стосується показника заломлення і щільності. Якщо я скажу вам щільність, ви зможете сказати мені показник заломлення. І якщо я скажу вам показник заломлення, ви зможете сказати мені щільність. Якщо розташувати речовини в порядку збільшення щільності, це також буде їх порядок збільшення показника заломлення.

Не зовсім вірно

Це не зовсім так, і, якщо ви витратите трохи під час пошуку щільності і показників заломлення речовин в, наприклад, CRC Довідник з фізики і хімії, ви знайдете безліч прикладів менш щільних речовин, що мають більш високий показник заломлення, ніж більш щільні речовини. Це правда в загальному сенсі зазвичай, що більш щільні речовини мають більш високі показники, але немає відповідності один до одного.

Насправді світло згинається до норми в «більш щільному» середовищі в результаті його повільнішої швидкості в цьому середовищі, і дійсно швидкість$v$ світла в середовищі показника заломлення$n$ задається

$$n = c/v, \label{eq:1.3.3}$$

$c$де швидкість світла у вакуумі. Тепер швидкість світла в середовищі є функцією електричної діелектричної проникності$\epsilon$ та магнітної проникності$\mu$:

$$v = 1 / \sqrt{ \epsilon \mu }. \label{eq:1.3.4}$$

Проникність більшості неферомагнітних середовищ дуже мало відрізняється від проникності вакууму, тому показник заломлення середовища задається приблизно

$$n \approx \sqrt{ \frac{ \epsilon }{ \epsilon_0 }} \label{eq:1.3.5}$$

Таким чином, існує набагато тісніша кореляція між показником заломлення і відносною діелектричною проникністю (діелектричної проникністю), ніж між показником заломлення і щільністю. Зверніть увагу, однак, що це лише приблизне відношення. У докладній теорії існує невелика залежність швидкості світла і, отже, показника заломлення від частоти (звідси і довжини хвилі) світла. При цьому показник заломлення більший для фіолетового світла, ніж для червоного (фіолетове світло заломлюється сильніше). Розщеплення білого світла на складові його кольори шляхом заломлення називається дисперсією.

Ось промінь світла, що подорожує від одного середовища до іншого:

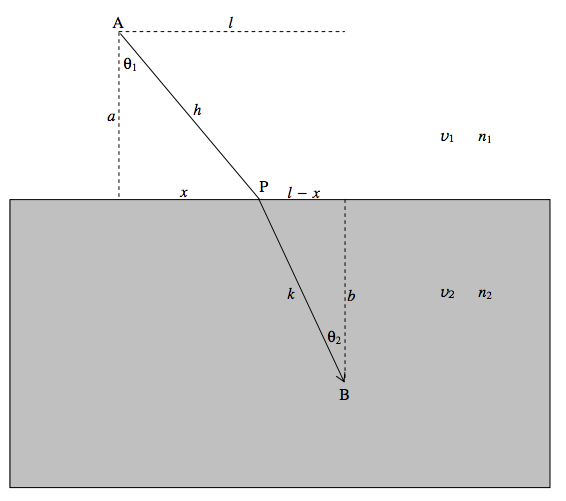
Він рухається швидше у верхньому середовищі, ніж у нижньому середовищі.

Час, необхідний для того, щоб дістатися від А до Б:

$$t = \frac{ \sqrt{ a^2 + x^2}}{ v_1} + \frac{ \sqrt{ b^2+(1-x)^2 }}{v^2}. \label{eq:1.3.6}$$

Тобто:

$$ct = n_1 \sqrt{ a^2 + x^2 } + n_2 \sqrt{ b^2 + (l -x)^2}. \label{eq:1.3.7}$$

Ось час, прийнятий в якості функції положення Р, розраховане для$n_2 / n_1 = 1.5$.

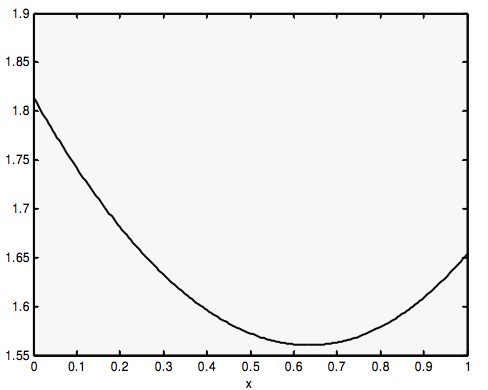
Як бачите, вона проходить мінімум. Ви можете знайти, де він знаходиться, диференціюючи рівняння$\ref{eq:1.3.7}$:

$$c \frac{ dt }{ dx } = \frac{ n_1x }{ \sqrt{ a^2 + x^2 }} - \frac{ n_2 ( l - x ) }{ \sqrt{ b^2 + ( l -x )^2 }} = n_1 \sin \theta_1 - n_2 \sin \theta_2, \label{eq:1.3.8}$$

Це нуль, коли$n_1 \sin \theta_1 − n_2 \sin \theta_2 = 0$. Таким чином, закон Снелла такий, що насправді пройдений шлях - це шлях, який займає найкоротший час. Тривіальна, або глибока?

Будівництво Гюйгенса

Ось хвильовий фронт, що рухається вгору. «Світлові «промені» є нормалями хвильового фронту.

Будівництво Гюйгенса - це спосіб передбачення того, що буде далі. Це говорить про те, що ви можете уявити кожну точку на хвильовому фронті, щоб бути джерелом, який генерує невеликий вейвлет. Потім, через деякий час хвилі виглядають так - і новий хвильовий фронт є загальною дотичною до всіх вейвлетів.

Спочатку це може здатися тривіальним, хоча про це написано багато - тобто чи представляє вона реальність, чи є просто зручною конструкцією. І, якщо реально, що відбувається з хвилетами в зворотному напрямку? Ми не будемо продовжувати це тут, але ми можемо використовувати конструкцію Гюйгенса як цікавий спосіб думати про закон Снелла.

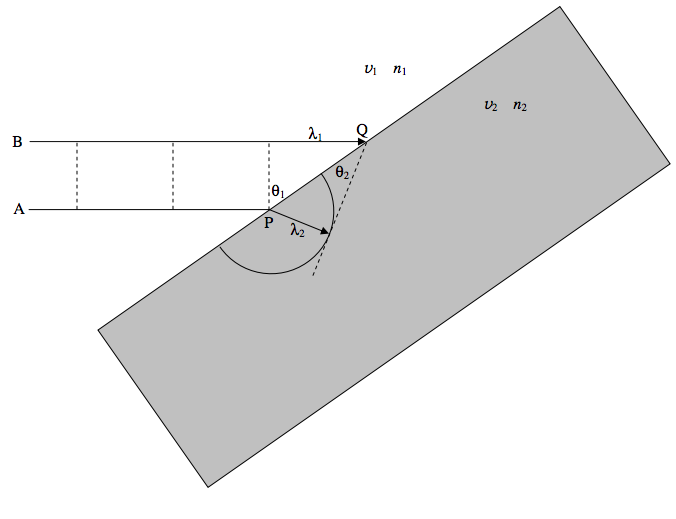
Промінь світла довжини хвилі$\lambda_1$ наближається до скляного блоку зліва зі швидкістю$v_1$. Пунктирні лінії представляють хвильові фронти. Промінь А досягає блоку першим, на P при P генерується вейвлет, рухаючись зі швидкістю$v_2$. Малюнок зроблений на той момент, коли промінь B досягає точки Q. новий хвильовий фронт - це тангенс від Q до маленького вейвлету, який розпочався в P. Геометрія покаже, що$\frac{ \lambda_1 } { \lambda_2 } = \frac{ v_1 }{ v_2 } = \frac{ n_2 }{ n_1}$ і тому$\sin \theta_1 = n_2 \sin \theta_2$.

Приклад$\PageIndex{1}$: Refraction through a glass block

На малюнку I.6 зображений промінь світла, що проходить через прямокутний скляний блок товщини$t$ і показника заломлення$n$ (прийнятий за 1,5 на кресленні). Нормаль до поверхні блоку робить кут$\theta$ з вхідним променем. Справа в простій геометрії (зроби це!) показати, що бічне$h$ зміщення променя задається

$$h = t ( \sin \theta - \cos \theta \tan \phi ), \label{eq:1.3.6.1}$$

де$\phi$ - кут заломлення, заданий$\sin \theta = n \sin \phi$. З точки зору$\theta, n$ і$t$, це

$$h = t \sin \theta \left( 1 - \frac{ \cos \theta }{ \sqrt{ n^2 - \sin^2 \theta }}\right). \label{eq:1.3.7.1}$$

Малюнок I.7 малюється для$n = 1.5$.

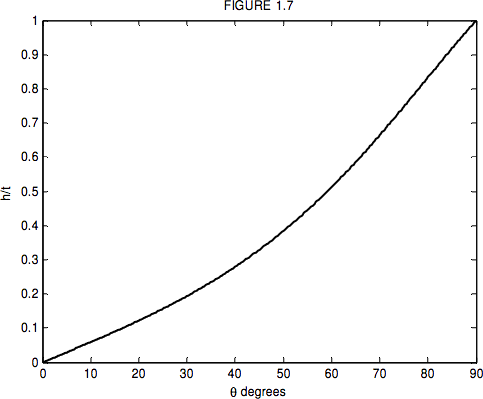
Можна собі уявити, використовуючи це для вимірювання відстані між двома точками, близькими один до одного. Наприклад, припустимо, що у вас є фотографія деяких зірок на старій фотопластині, і вона включає близьку пару зірок, і ви хочете виміряти відстань між двома зображеннями зірок. (Сьогодні фотографія була б на ПЗС-детекторі, а відстань між двома зображеннями записується в електронному вигляді, тому я вказую стару фотографічну табличку.) Ви дивитесь на фотографію через мікроскоп і бачите одну з зірок, розділених перехрестям, в окулярі мікроскопа. Але перед фотографією у вас є скляна пластина, і ви нахиляєте тарілку, щоб змістити зображення так, щоб зображення рухалися, а друга зірка тепер розділена перехрестям. З великого кута, через який ви нахиляєте тарілку, ви можете відпрацювати крихітну відстань між двома зображеннями. Ви хочете використовувати монохроматичне світло, і вам потрібно знати показник заломлення на цій довжині хвилі.

Як ви будете вимірювати кут, через який розгорнулася пластина? Ну, ви могли б світити лазерний промінь від нього; відбите світло буде рухатися з подвійною швидкістю пластини, і ви можете дозволити їй висвітлити аркуш графічного паперу на відстані декількох футів. Таким чином, крихітна відстань між зображеннями буде відповідати великій відстані на графічному папері. Може бути одна або дві інші практичні деталі, про які ви хочете подумати. Наприклад, наскільки товстою ви хочете, щоб скляна пластина була? Тонкий слайд мікроскопа, може, або щось набагато товщі, ніж це? Чи було б краще працювати під кутами$\theta$ менше, ніж приблизно 40º, де нахил малюнка I.7 невеликий, або під кутами більше 50º, де нахил більший?

Ви також можете перемістити лазерний промінь вбік через невелику і контрольовану кількість. Ви можете поставити скляний блок на поворотний стіл, який можна повернути через крихітний вимірюваний кут і таким чином переміщати лазерний промінь збоку і точно через дуже крихітну кількість.

Продовжимо зі склоблоком.

Приклад$\PageIndex{2}$: Refraction through a moving glass block

Покажіть, що, якби скляний блок обертався проти годинникової стрілки з кутовою швидкістю$\omega$, лазерний промінь рухався б вгору зі швидкістю

$$\dot{h} = t \left[ \cos \theta - \frac{ n^2 - 2n^2 \sin^2 \theta + \sin^4 \theta }{ ( n^2 - \sin^2 \theta )^{3/2} }\right]\omega \label{eq:1.3.8.1}$$

Якщо ми пишемо$\sin^2 \theta$ як$1 - \cos^2 \theta$, ми зможемо висловити це цілком з точки зору$\cos \theta$. І якщо для ілюстративних цілей я візьму$n = 1.5$, рівняння стає

$$\frac{ \dot{h}}{ t \omega } = c + \frac{ 1.25 - 2.5c^2 - c^4 }{ (1.25 + c^2 ) ^ {3/2}}, \label{eq:1.3.9}$$

де$c = \cos \theta$. Для зручності в обчисленні я поставлю$C = c^2$. Рівняння$\ref{eq:1.3.9}$ тоді стає

$$\frac{ \dot{h}}{ t \omega } = c + \frac{ 1.25 - C(2.5+C)}{ (1.25 +C ) ^ {3/2}}. \label{eq:1.4.0}$$

Це легко обчислити, а результат показаний на графіку нижче.

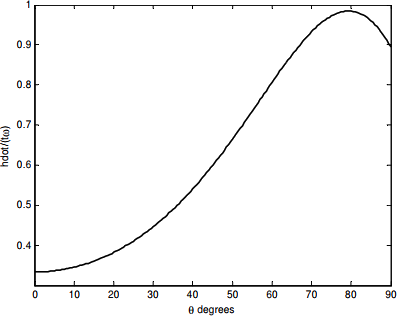
Ми бачимо, можливо, на наш подив, що$\dot{h}$ & проходить максимум при приблизно$\theta$ = 79º. Щоб отримати рівняння$\ref{eq:1.3.9}$, нам довелося диференціювати рівняння$\ref{eq:1.3.7}$. Тепер, щоб з'ясувати, де$\dot{h}$ проходить максимум, нам доведеться знову диференціювати, хоча милостиво ми можемо диференціювати рівняння$\ref{eq:1.4.0}$ відносно,$C$ а не до$\theta$. Якщо ми це зробимо, а потім встановимо похідну в нуль, ми знаходимо, після деякого спрощення,

$$\frac{ 1 }{ 2C^{1/2 }} = \frac{ 5 + 1.25C + 0.5C^2 }{ (1.25 + C)^{5/2}} \label{eq:1.4.1}$$

Якщо ми квадратимо це і збираємо повноваження$C$, ми дійдемо до рівняння чверті в$C$:

$625 - 17980C - 6240C^2 - 2176C^3 + 256C^4 = 0.$

де$C = c^2 = \cos^2 \theta$.

Рішення цього рівняння є$C = 0.034 346 549 0$, відповідним

$\theta$= 79º.319 731 1