1.7: Веселка

Last updated
Save as PDF

Page ID: 79056

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Я не знаю точної форми краплі дощу, але я дуже сумніваюся, якщо вона каплевидна! Більшість крапель дощу будуть більш-менш сферичними, особливо дрібними краплями, через поверхневого натягу. Якщо великі падаючі краплі спотворюються від точної сферичної форми, я думаю, що вони, швидше за все, будуть сплющені до якоїсь горизонтальної форми млинця, а не до форми краплі. Незважаючи на це, при аналізі в цьому розділі я припускаю, що краплі сферичні, оскільки я впевнений, що невеликі краплі будуть.

Ми хочемо слідувати за світловим променем, коли він входить у сферичну краплю, внутрішньо відбивається і, нарешті, з'являється. Див. Малюнок I.15. Ми будемо називати відстань\(b\) параметром удару.

Ми бачимо промінь світла, спрямований на краплю, яку я беру, щоб мати радіус одиниці, на параметр удару\(b\). Відхилення напрямку виходить променя від напрямку падаючого променя дорівнює

\[D = \theta - \theta' + \pi -2\theta' +\theta - \theta' = \pi + 2\theta - 4\theta'. \label{eq:1.7.1} \]

Однак нас буде більше цікавити кут\(r = \pi − D\). Промінь світла, який був відхилений,\(D\) буде наближатися до спостерігача з напрямку, який робить кут\(r\) від центру лука, який знаходиться в антисонячній точці (рис. I.16)

Ми хотіли б знайти відхилення\(D\) як функцію параметра впливу. Кути падіння і заломлення пов'язані з параметром удару наступним чином:

\[\sin\theta=b,\label{eq:1.7.2} \]

\[\cos\theta=\sqrt{1-b^2},\label{eq:1.7.3} \]

\[\sin\theta' = b/n,\label{eq:1.7.4} \]

\[ \cos\theta = \sqrt{1-b^2/n^2}. \label{eq:1.7.5} \]

Вони разом з рівнянням\(\ref{eq:1.7.1}\) дають нам відхилення як функцію параметра впливу. Відхилення проходить через мінімум — і\(r\) проходить максимум. Відхилення для світлового променя параметра удару\(b\) дорівнює

\[D = \pi + 2\sin^{-1}b - 4\sin^{-1}(b/n)\label{eq:1.7.6} \]

Кутова відстань\(r\) від центру носової частини становить\(r = \pi − D\), так що

\[r = 4 \sin^{-1}(b/n) - 2\sin^{-1}b.\label{eq:1.7.7} \]

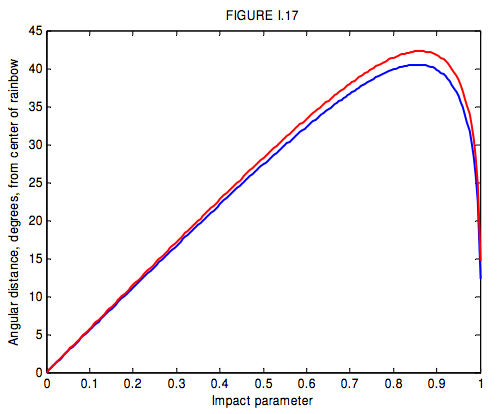
Це показано на малюнку I.17 для\(n\) = 1,3439 (синій -\(\gamma\) = 400 нм) і\(n\) = 1,3316 (червоний -\(\gamma\) = 650 нм).

Диференціація дає максимальне значення\(R\), of\(r\) - тобто радіус носової частини - або мінімальне відхилення\(D_{\text{min}}\). Отримуємо для радіуса лука

\[R = 4\sin^{-1}\sqrt{\frac{4-n^2}{3n^2}}- 2\sin^{-1}\sqrt{\frac{4-n^2}{3}}. \label{eq:1.7.8} \]

Для\(n\) = 1.3439 (синій) це 40 ° 31', а для\(n\) = 1.3316 (червоний) це 42 ° 17'. Таким чином синій знаходиться на внутрішній стороні лука, а червоний на зовнішній.

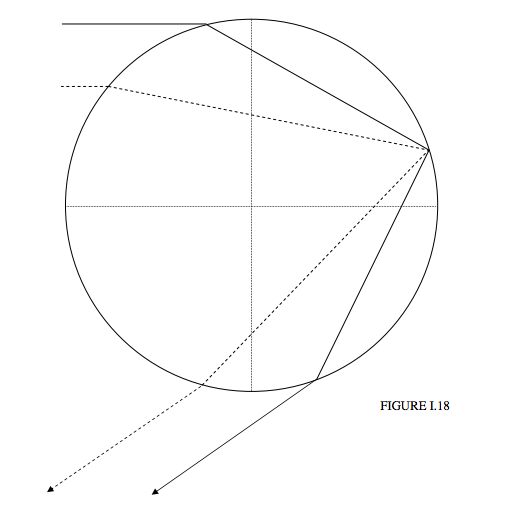
Для випасу випасу (параметр впливу = 1) відхилення становить\( 2 \pi -4 \sin^{-1}(1/n)\), або 167 ° 40' для синього або 165 ° 18' для червоного. Це відповідає відстані від центру лука\( r = 4 \sin^{-1}(1/n)-\pi\), яка становить '12 ° 20' для синього і 14 ° 42' для червоного. З малюнка I.17 видно, що для радіусів менше\(R\) (тобто всередині веселки), але більше 12 ° 20' для синього і 14 ° 42' для червоного є два параметри удару, які призводять до того ж відхилення, тобто в тому ж положенні всередині лука. Шляхи двох променів з однаковим відхиленням показані на малюнку I.18. Один промінь малюється як повна лінія, інший - пунктирною лінією. Вони починаються з різних параметрів удару, і проходять різні шляхи через краплю, але закінчують в одному напрямку. Креслення робиться для відхилення 145 °, або 35 ° від центру носової частини. Два параметри впливу - 0,969 і 0,636. Коли ці два промені рекомбінуються шляхом фокусування на сітківці ока, вони задовольняють всі умови для перешкод, і результатом буде яскравість або темрява відповідно до того, чи є різниця шляху парною або непарною кількістю половини довжин хвиль.

Якщо заглянути тільки всередину внутрішнього (синього) краю лука, то часто можна чітко побачити інтерференційні бахроми, вироблені двома променями з однаковим відхиленням. Я не пробував, але якщо ви переглянете фільтр, який передає лише один колір, ці бахроми (якщо вони досить яскраві, щоб побачити) повинні бути чітко визначені. Оптична різниця шляху для даного відхилення, або заданого\(r\), залежить від радіуса краплі (і від його показника заломлення). Для краплі радіуса\(a\) легко побачити, що різниця оптичного шляху

\( 2a(\cos\theta_2 - \cos\theta_1) - 4n(\cos\theta'_2-\cos\theta'_1),\)

де\(\theta_1\) більший з двох кутів падіння. Імовірно, якби ви вимірювали відстань між бахромою, ви могли б визначити розмір крапель. Або, якби вам довелося провести Фур'є аналіз видимості окантовки, ви могли б визначити, принаймні в принципі, розмірний розподіл крапель.

Деяка відстань поза основною веселкою, є вторинна веселка, з кольорами зворотні - тобто червоний на внутрішній стороні, синій зовні. Це утворено двома внутрішніми відображеннями всередині краплі (рис. I.19). Відхилення кінцевого з'являється променя від напрямку падаючого променя становить\((\theta − \theta') + (π − 2\theta') + (π − 2\theta') + (\theta − \theta')\), або\(2π + 2\theta − 6\theta'\) проти годинникової стрілки, що дорівнює годинниковій\(D = 6\theta' − 2\theta\) стрілці. Тобто,

\[ D = 6\sin^{-1}(b/n)-2\sin^{-1}b. \label{eq:1.7.9} \]

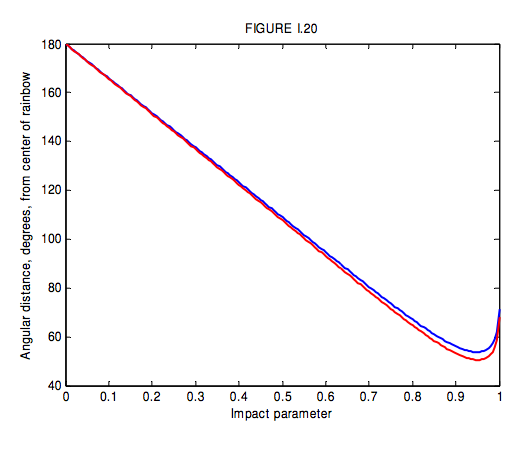
за годинниковою стрілкою, і, як і раніше, це відповідає кутовій відстані від центру лука\(r = \pi − D\). Я показую на малюнку I.20 кутову відстань від центру лука проти параметра удару\(b\). Зверніть увагу, що\(D\) проходить максимум і, отже,\(r\) має мінімальне значення. Немає світла, розсіяного за межами первинного лука, і немає світла, розсіяного всередині вторинного лука. Коли спостерігається повна слава первинного лука та вторинного лука, буде видно, що простір між двома луками відносно темний, тоді як він яскравіший всередині первинного лука та зовні вторинного лука.

Диференціація показує, що найменша величина\(r\), (найбільше відхилення), що відповідає радіусу вторинного лука, є

\[R = 6\sin^{-1} \sqrt{\frac{3-n^2}{2n^2}} - 2\sin^{-1}\sqrt{\frac{3-n^2}{2}}\label{eq:1.7.10} \]

Для\(n = 1.3439\) (синього) це 53° 42', а для\(n = 1.3316\) (червоний) це 50° 31'. Таким чином червоний знаходиться на внутрішній стороні лука, а синій на зовнішній.

В принципі можливий третинний уклін, що включає в себе три внутрішні роздуми. Я не знаю, чи хтось спостерігав третинний лук, але мені кажуть, що основний лук синій зсередини, вторинний лук - червоний зсередини, і «отже» третинний лук був би синім зсередини. Навпаки, я стверджую, що третинний лук був би червоним зсередини. Чому це?

Повернемося до первинного лука. Відхилення є (Рівняння\(\ref{eq:1.7.1}\))\(D = π + 2\theta − 4\theta'\). Давайте візьмемо\(n = 4/3\), для чого це буде десь посередині спектра. Відповідно до Рівняння\(\ref{eq:1.7.8}\), радіус носової\((R = \pi − D_{\text{min}})\) частини тоді становить близько 42°. Тобто\(2\theta' − \theta\) = 21°. Якщо ми поєднаємо це із законом Снелла\(3\sin \theta = 4\sin \theta'\), то виявимо, що при мінімальному відхиленні (тобто там, де основний лук),\(\theta\) = 60°.5 і\(\theta'\) = 40°.8. Тепер у точці внутрішнього відбиття відбивається не все світло (тому що\(\theta'\) менше критичного кута 36°.9), і буде видно, що кут між відбитими і заломленими променями становить (180 − 60,6 − 40,8) градусів = 78°.6. Ті читачі, які знайомі з законом Брюстера, зрозуміють, що коли відбиті і передані промені знаходяться під прямим кутом один до одного, відбитий промінь повністю плоский поляризований. Кут, як ми бачили, не 90°, а становить 78°.6, але це досить близько до умови Брюстера, що відбите світло, хоча і не повністю плоске поляризоване, сильно поляризоване. Таким чином, як можна переконатися за допомогою поляризаційного фільтра, веселка сильно плоска поляризована.

Зараз я хочу звернутися до питання про те, як змінюється яскравість лука від центру до кола. Найяскравіше, коли нахил кривої відхилення від параметра удару найменший - тобто при мінімальному відхиленні (для первинного лука) або максимальному відхиленні (для вторинного лука). Дійсно, сяйво (яскравість поверхні) на заданій відстані від центру лука (серед іншого) обернено пропорційно нахилу цієї кривої. Ситуація трохи ускладнюється тим, що для відхилень між\(D_{\text{min}}\) і\(2\pi - 4\sin^{-1}(1/n)\), (це останнє відхилення для випасу випасу), є два параметри удару, що породжують однакове відхилення, але для відхилень більше, ніж це (тобто ближче до центру носової частини) тільки один удар параметр відповідає заданому відхиленню.

Давайте запитаємо себе, наприклад, наскільки яскравим є лук на 35° від центру (відхилення 145°)? Відхилення пов'язане з параметром впливу рівнянням\(\ref{eq:1.7.6}\). Для\(n = 4/3\), знайдемо, що параметри впливу при відхиленнях 144, 145 і 146 градусів такі:

Д°	б
144	0,6583 та 0,9623
145	0,6366 та 0,9693
146	0,6157 та 0,9736

На малюнку I.21 показана крапля дощу, помічена з напрямку наближаються фотонів.

Будь-які фотони з параметрами удару в межах двох темних аннулів будуть відхилені між 144° і 146° і в кінцевому підсумку наближаються до спостерігача на кутових відстанях між 36° і 34° від центру. Сяйво на відстані 35° від центру буде пропорційно, серед іншого, сумі площ цих двох річних.

Я сказав «серед іншого». Давайте тепер подумаємо про інші речі. Я намалював малюнок I.15 так, ніби все світло передається, коли воно потрапляє в краплю, а потім все це внутрішньо відбивається всередині краплі, і, нарешті, все це з'являється, коли він залишає краплю. Це не так, звичайно. При вході, при внутрішньому відображенні і при появі частина світла відбивається, а частина передається. Дроби, які відбиваються або передаються, залежать від кута падіння, але, при мінімальному відхиленні, близько 94% передається при вході в і знову при виході з краплі, але внутрішньо відбивається лише близько 6%. Також після входу, внутрішнього відображення і виходу збільшується відсоток поляризації променя. Формули коефіцієнтів відбиття та пропускання (рівняння Френеля) дещо складні (Рівняння 1.5.1 та 1.5.2) призначені для неполяризованого падаючого світла), але я дотримувався їх через як функцію параметра удару, а також врахував розміри один або два аннулі беруть участь для кожного параметра удару, і я, отже, розрахував варіацію яскравості поверхні для одного кольору\((n = 4/3)\) від центру до окружності лука. Я опускаю деталі розрахунків, так як ця глава спочатку планувалася як елементарний рахунок відображення і передачі, і ми, здається, вийшли трохи далі цього, але результати розрахунку я показую на малюнку I.22. Я, однак, не врахував інтерференційні явища, які часто можна чітко побачити тільки в межах первинного лука.