1.3:1.3 Функція логарифма

Last updated
Save as PDF

Page ID: 79745

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)

Оскільки експоненціальна є функцією один до одного, її зворотна є чітко визначеною функцією. Ми називаємо це натуральним логарифмом:\[\label{eq:1}\ln(x) \equiv y \;\; \mathrm{such}~\mathrm{that}\; \exp(y) = x.\] Для стислості ми відтепер будемо використовувати «логарифм» для позначення натурального логарифма, якщо не вказано інше («ненатуральні» логарифми не є нашою турботою в цьому курсі). Домен логарифма є\(y \in \mathbb{R}^+\), а його діапазон -\(\mathbb{R}\). Її графік наведено нижче:

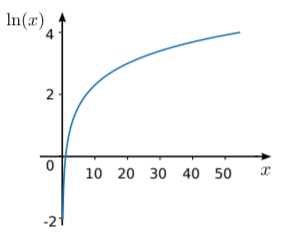
Зверніть увагу, що графік збільшується надзвичайно повільно з\(x\), точно протилежним поведінці експоненціального.

Використовуючи Eq. (1.2.3), ми можемо довести, що логарифм задовольняє правилам добутку і частки\[\begin{align} \ln(xy) &= \ln(x) + \ln(y) \\ \ln(x/y) &= \ln(x) - \ln(y).\end{align}\]