29.4: Ідеальний газ

Розглянемо газ, що складається з великої кількості молекул всередині жорсткої ємності. Будемо вважати, що обсяг, який займають молекули, невеликий в порівнянні з обсягом, займаним газом, тобто обсягом ємності (припущення розбавленого газу). Ми також припускаємо, що молекули рухаються випадковим чином і задовольняють Закони руху Ньютона. Молекули газу стикаються між собою і стінками ємності. Будемо вважати, що всі зіткнення є миттєвими і будь-яка енергія, перетворена в потенційну енергію під час зіткнення, відновлюється як кінетична енергія після завершення зіткнення. Таким чином, зіткнення пружні і мають ефект зміни напрямку швидкостей молекул, але не їх швидкості. Ми також припускаємо, що міжмолекулярні взаємодії вносять незначний внесок у внутрішню енергію.

Внутрішня енергія одноатомного газу

Ідеальний одноатомний атом газу не має внутрішньої структури, тому ми розглядаємо його як точкову частинку. Тому не існує можливих обертальних ступенів свободи або внутрішніх ступенів свободи; ідеальний газ має лише три ступені свободи, а внутрішня енергія ідеального газу\[E_{\text {intemal }}=N \frac{3}{2} k T \nonumber \] Рівняння (29.4.1) називається тепловим рівнянням стану одноатомного ідеального газу. Середня кінетична енергія кожного ідеального атома\[\frac{1}{2} m\left(v^{2}\right)_{\mathrm{ave}}=\frac{3}{2} k T \nonumber \] газу\(\left(v^{2}\right)_{\text {ave }}\) - це середнє значення квадрата швидкостей і задається\[\left(v^{2}\right)_{\mathrm{ave}}=\frac{3 k T}{m} \nonumber \] Температура цього ідеального газу пропорційна середній кінетичній молекули ідеального газу. Це неправильний висновок сказати, що температура визначається як середня кінетична енергія газу. При низьких температурах або нерозбавлених щільностях кінетична енергія вже не пропорційна температурі. Для деяких газів кінетична енергія залежить від щільності чисел і більш складної залежності від температури, ніж та, що наведена в Рівнянні (29.4.2).

Тиск ідеального газу

Розглянемо ідеальний газ, що складається з великої кількості N однакових молекул газу, кожна масою m, всередині ємності об'ємом V і тиском P. Число молекул газу на одиницю об'єму тоді\(n = N / V\). Щільність газу дорівнює\(\rho = nm\). Молекули газу пружно стикаються один з одним і стінками ємності. Тиск, який газ чинить на ємність, обумовлено пружними зіткненнями молекул газу зі стінками ємності. Тепер ми будемо використовувати поняття енергії та імпульсу для моделювання зіткнень між молекулами газу та стінками контейнера, щоб визначити тиск газу через об'єм V, число частинок N і температуру Кельвіна T.

Рисунок 29.2 Зіткнення молекули газу зі стінкою контейнера

Почнемо з розгляду зіткнення однієї молекули з однією зі стінок контейнера, орієнтованого з одиничним нормальним вектором, що вказує з контейнера в позитивному\(\hat{\mathbf{i}}\) -напрямку (рис. 29.2). Припустимо, молекула має масу m і рухається зі швидкістю\(\overrightarrow{\mathbf{v}}=v_{x} \hat{\mathbf{i}}+v_{y} \hat{\mathbf{j}}+v_{z} \hat{\mathbf{k}}\). Оскільки зіткнення зі стінкою пружне, y -і z - складові швидкості молекули залишаються постійними і х-складова знака зміни швидкості (рис. 29.2), в результаті чого відбувається зміна імпульсу молекули газу;\[\Delta \overrightarrow{\mathbf{p}}_{m}=\overrightarrow{\mathbf{p}}_{m, f}-\overrightarrow{\mathbf{p}}_{m, i}=-2 m v_{x} \hat{\mathbf{i}} \nonumber \] тому імпульс, що передається молекулою газу на Стінка\[\Delta \overrightarrow{\mathbf{p}}_{w}=2 m v_{x} \hat{\mathbf{i}} \nonumber \] тепер, давайте розглянемо ефект зіткнень великої кількості випадково рухаються молекул. Для наших цілей «випадковим» буде прийнято вважати, що будь-який напрямок руху можливий, а розподіл складових швидкості однаковий для кожного напрямку.

Малюнок 29.3 Малий обсяг, що примикає до стінки контейнера

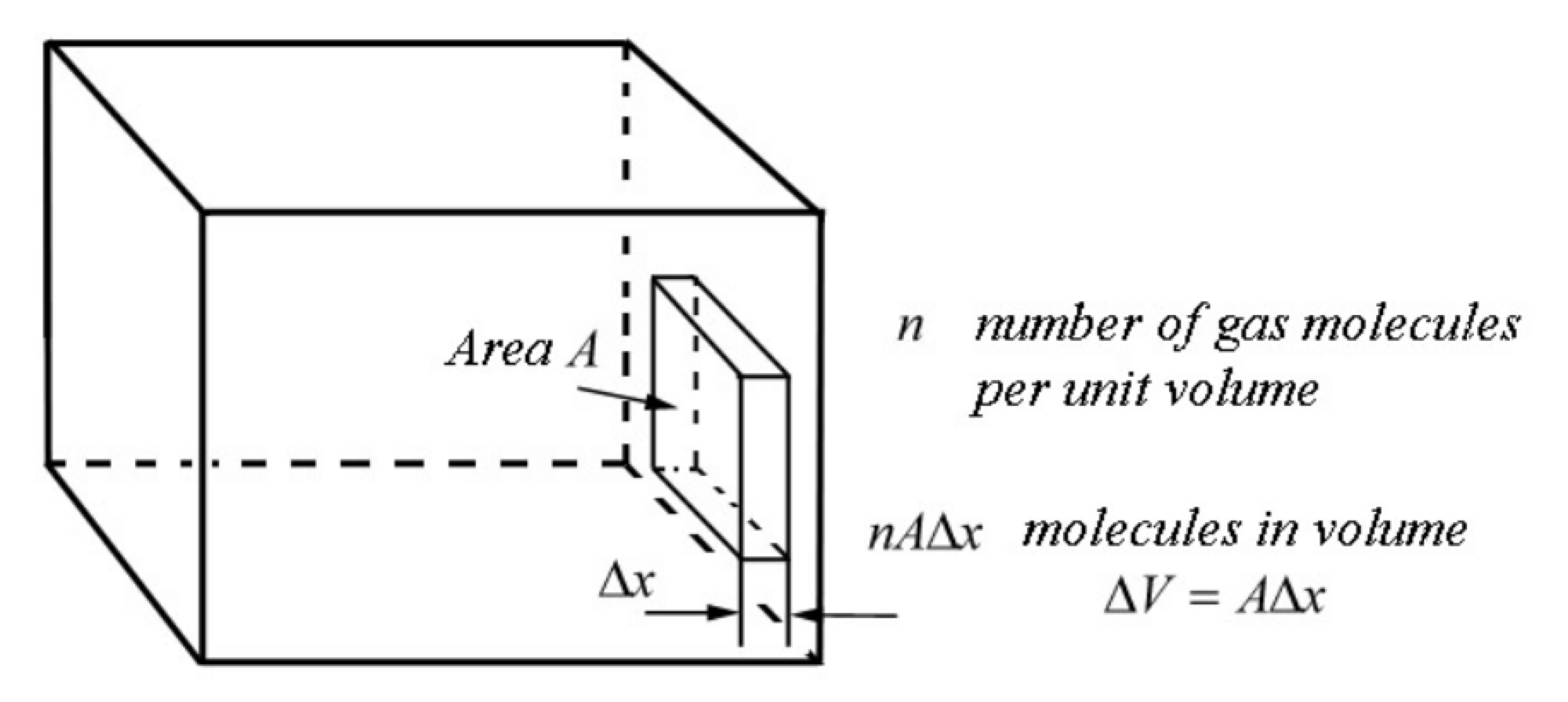
Розглянемо невеликий прямокутний\(\Delta V=A \Delta x\) обсяг газу, що примикає до однієї зі стінок ємності, як показано на малюнку 29.3. У цьому невеликому обсязі знаходяться молекули\(n A \Delta x\) газу. Нехай кожна група має однакову x-складову швидкості. Нехай\(n_{j}\) позначимо кількість молекул газу в\(j^{t h}\) групі з х -складовою швидкості\(v_{x, j}\). Оскільки молекули газу рухаються випадковим чином, лише половина молекул газу в кожній групі буде рухатися до стінки в позитивному напрямку x. Тому в часовому інтервалі кількість молекул газу\(\Delta t_{j}=\Delta x / v_{x, j}\), які вражають стінку з х-складовою швидкості\(\mathcal{V}_{x, j}\) задається\[\Delta n_{j}=\frac{1}{2} n_{j} A \Delta x \nonumber \] (Протягом цього часового інтервалу деякі молекули газу можуть покинути краю коробки, а тому число, яке перетинає площу в секунду, пропорційно площа, в межі як Δx → 0, число, що виходить з ребер, також наближається до нуля.) Кількість молекул газу в секунду дорівнює тоді\[\frac{\Delta n_{j}}{\Delta t_{j}}=\frac{1}{2} n_{j} A \frac{\Delta x}{\Delta t_{j}}=\frac{1}{2} n_{j} A v_{x, j} \nonumber \] Імпульс в секунду, який молекули газу в цій групі доставляють до стінки, - це За другим\[\frac{\Delta \overrightarrow{\mathbf{p}}_{j}}{\Delta t_{j}}=\frac{\Delta n_{j}}{\Delta t_{j}} 2 m v_{x, j} \hat{\mathbf{j}}=n_{j} m A v_{x, j}^{2} \hat{\mathbf{i}} \nonumber \] законом Ньютона середня сила на стінці завдяки цій групі молекул дорівнює імпульсу в секунду, що доставляється молекулами газу до стінка;\[\left(\overrightarrow{\mathbf{F}}_{j, w}\right)_{\mathrm{ave}}=\frac{\Delta \overrightarrow{\mathbf{p}}_{j}}{\Delta t_{j}}=n_{j} m A v_{x, j}^{2} \hat{\mathbf{i}} \nonumber \] Тиск, що вноситься цією групою молекул газу, є тоді\[P_{j}=\frac{\left|\left(\overrightarrow{\mathbf{F}}_{j, w}\right)_{\mathrm{ave}}\right|}{A}=n_{j} m v_{x, j}^{2} \nonumber \] Тиск, що чиниться всіма групами молекул газу, є сумою\[P=\sum_{j=1}^{j=N_{g}}\left(P_{j}\right)_{\text {ave }}=m \sum_{j=1}^{j=N_{g}} n_{j} v_{x, j}^{2} \nonumber \]. Середнє значення квадрата х -складової швидкості задається тим,\[\left(v_{x}^{2}\right)_{\text {ave }}=\frac{1}{n} \sum_{j=1}^{j=N_{g}} n_{j} v_{x, j}^{2} \nonumber \] де n - кількість молекул газу на одиницю обсяг в контейнері. Тому ми можемо переписати рівняння (29.4.11) як\[P=m n\left(v_{x}^{2}\right)_{\text {ave }}=\rho\left(v_{x}^{2}\right)_{\text {ave }} \nonumber \] де\(\rho\) щільність газу. Оскільки ми припустили, що молекули газу рухаються випадковим чином, середнє значення квадрата x -, y - і z -складових швидкості руху молекул газу рівні,\[\left(v_{x}^{2}\right)_{\text {ave }}=\left(v_{y}^{2}\right)_{\text {ave }}=\left(v_{z}^{2}\right)_{\text {ave }} \nonumber \] середнє значення квадрата швидкості\(\left(v^{2}\right)_{\text {ave }}\) дорівнює сумі середніх квадратів складових швидкість,\[\left(v^{2}\right)_{\text {ave }}=\left(v_{x}^{2}\right)_{\text {ave }}+\left(v_{y}^{2}\right)_{\text {ave }}+\left(v_{z}^{2}\right)_{\text {ave }} \nonumber \]. Тому\[\left(v^{2}\right)_{\text {ave }}=3\left(v_{x}^{2}\right)_{\text {ave }} \nonumber \] підставляючи рівняння (29.4.16) у рівняння (29.4.13) для тиску виходу газу\[P=\frac{1}{3} \rho\left(v^{2}\right)_{\mathrm{ave}} \nonumber \]

Квадратний корінь\(\left(v^{2}\right)_{\text {ave }}\) називається середньоквадратичної («середньоквадратичної») швидкістю молекул

Заміна рівняння (29.4.3) на рівняння (29.4.17) дає\[P=\frac{\rho k T}{m} \nonumber \] Згадаймо, що щільність газу\[\rho=\frac{M}{V}=\frac{N m}{V} \nonumber \] Тому рівняння (29.4.18) може бути перезаписано як\[P=\frac{N k T}{V} \nonumber \] рівняння (29.4.20) може бути повторно виражене як\[P V=N k T \nonumber \] рівняння (29.4.21) відоме як рівняння ідеального газу також відомий як Закон про ідеальний газ або Закон про ідеальний газ.

Загальна кількість молекул в газі\(N=n_{\mathrm{m}} N_{A}\) де\(n_{\mathrm{m}}\) число молей і\(N_{A}\) є постійною Авогадро. Ідеальним газовим законом стає\[P V=n_{\mathrm{m}} N_{A} k T \nonumber \] Універсальна газова константа є\(R=k N_{A}=8.31 \mathrm{J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\). Закон ідеального газу може бути повторно виражений як\[P V=n_{\mathrm{m}} R T \nonumber \] Хоча ми почали з атомістичного опису зіткнень окремих молекул газу, що задовольняють принципам збереження енергії та імпульсу, ми закінчилися взаємозв'язком між макроскопічними змінними тиском, об'ємом, кількістю молів, і температури, які є вимірюваними властивостями системи.

Одним з важливих наслідків закону ідеального газу є те, що рівні обсяги різних ідеальних газів при однаковій температурі і тиску повинні містити однакову кількість молекул,\[N=\frac{1}{k} \frac{P V}{T} \nonumber \] Коли гази об'єднуються в хімічних реакціях при постійній температурі і тиску, числа кожного типу молекул газу об'єднуються в простих невід'ємних пропорціях. З цього випливає, що обсяги газів завжди повинні бути в простих цілісних пропорціях. Авогадро використовував це останнє спостереження щодо газових реакцій, щоб визначити один моль газу як одиницю для великої кількості частинок.