29.5: Атмосфера
- Page ID
- 75820
Атмосфера являє собою дуже складну динамічну взаємодію між багатьма різними видами атомів і молекул. Середній процентний склад одинадцяти найбільш поширених газів в атмосфері до висоти 25 км наведені в таблиці 1.
Таблиця 1: Середній склад атмосфери до висоти 25 км.
| Назва газу | Хімічна формула | Відсоток об'єму |
| Азот | \({N}_{2}\) | 78.08% |
| Кисень | \({O}_{2}\) | 20,95% |
| *Вода | \({H}_{2}O\) | Від 0 до 4% |
| Аргон | \(Ar\) | 0,93% |
| * Вуглекислий газ | \({CO}_{2}\) | 0,0360% |
| Неонові | \(Ne\) | 0,0018% |
| Гелій | \(He\) | 0,0005% |
| * Метан | \(\mathrm{CH}_{4}\) | 0.00017% |
| Водень | \(H_{2}\) | 0,00005% |
| * Закис азоту | \(\mathrm{N}_{2} \mathrm{O}\) | 0,00003% |
| * Озон | \(O_{3}\) | 0,000004% |
* змінні гази
В атмосфері азот утворює двоатомну молекулу з молярною масою,\(M_{\mathrm{N}_{2}}=28.0 \mathrm{g} \cdot \mathrm{mol}^{-1}\) а кисень також утворює двоатомну молекулу\(O_{2}\) з молярною масою\(M_{\mathrm{O}}=32.0 \mathrm{g} \cdot \mathrm{mol}^{-1}\). Оскільки ці два гази об'єднуються, утворюючи 99% атмосфери, середня молярна маса O2 атмосфери становить\[M_{\mathrm{atm}} \simeq(0.78)\left(28.0 \mathrm{g} \cdot \mathrm{mol}^{-1}\right)+(0.21)\left(32.0 \mathrm{g} \cdot \mathrm{mol}^{-1}\right)=28.6 \mathrm{g} \cdot \mathrm{mol}^{-1} \nonumber \]
\(\rho\)Щільність атмосфери як функція молярної маси\(M_{\mathrm{atm}}\), об'єму V і атм кількості молів,\(n_{m}\) що містяться в обсязі, задається\[\rho=\frac{M^{\text {total }}}{V}=\frac{n_{\mathrm{m}} M_{\text {molar }}}{V} \nonumber \] Як змінюється тиск атмосфери залежно від висоти над поверхнею землі? На малюнку 29.4 висота над рівнем моря в кілометрах побудована проти тиску. (Також на графіку нанесена функція висоти щільність в кілограмах на кубічний метр.)

Ізотермічна ідеальна газова атмосфера
Змоделюємо атмосферу як ідеальний газ в статичній рівновазі при постійній температурі\(T=250 \mathrm{K}\). Тиск на поверхні землі є\(P_{0}=1.02 \times 10^{5} \mathrm{Pa}\). Тиск ідеального газу, використовуючи рівняння стану ідеального газу (Рівняння (29.4.23)) може бути виражено через тиск P, універсальної газової постійної R, молярної маси\(M_{\mathrm{atm}}\) атмосфери і температури T,\[P=n_{\mathrm{m}} R \frac{T}{V}=\frac{M^{\text {total }}}{V} \frac{R T}{M_{\text {atm }}}=\rho \frac{R T}{M_{\text {atm }}} \nonumber \] Таким чином рівняння стану для щільності газу може бути виражено як \[\rho=\frac{M_{\text {atm }}}{R T} P \nonumber \]За допомогою другого закону Ньютона визначаємо умову про сили, що діють на малий циліндричний об'єм атмосфери (рис. 29.5а) в статичній рівновазі площі перерізу А, розташованої між висотами\(z\) і\(z+\Delta z\)

Маса, що міститься в цьому елементі, є добутком щільності\(\rho\) і об'ємного елемента\(\Delta V=A \Delta z\),\[\Delta m=\rho \Delta V=\rho A \Delta z \nonumber \]
Сила внаслідок тиску на верхню частину циліндра спрямована вниз і дорівнює\(\overrightarrow{\mathbf{F}}(z+\Delta z)=-P(z+\Delta z) A \hat{\mathbf{k}}\) (рис. 29.5 (б)), де\(\hat{\mathbf{k}}\) - одиничний вектор, спрямований вгору. Сила внаслідок тиску на дно циліндра спрямована вгору і дорівнює\(\overrightarrow{\mathbf{F}}(z)=P(z) A \hat{\mathbf{k}}\). Тиск на верх\(P(z+\Delta z)\) і\(P(z)\) низ цього елемента не рівні, а відрізняються на величину\(\Delta P=P(z+\Delta z)-P(z)\). Діаграма сили для цього елемента показана на малюнку 29.5б.
Оскільки атмосфера знаходиться в статичній рівновазі в нашій моделі, сума сил на об'ємному елементі дорівнює нулю,\[\overrightarrow{\mathbf{F}}^{\text {total }}=\Delta m \overrightarrow{\mathbf{a}}=\overrightarrow{\mathbf{0}} \nonumber \] Таким чином умова статичної рівноваги сил у напрямку z -це\[-P(z+\Delta z) A+P(z) A-\Delta m g=0 \nonumber \] Зміна тиску потім задається\[\Delta P A=-\Delta m g \nonumber \] використанням рівняння (29.5.5) для маси Δm, підставити в Рівняння (29.5.8),\[\Delta P A=-\rho A \Delta z g=-\frac{M_{\mathrm{atm}} g}{R T} A \Delta z P \nonumber \] що дає Похідна тиску як функція висоти, то лінійно пропорційна тиску,\[\frac{d P}{d z}=\lim _{\Delta z \rightarrow 0} \frac{\Delta P}{\Delta z}=-\frac{M_{\text {atm }} g}{R T} P \nonumber \] Це відокремлюване диференціальне рівняння; розділення змінних,\[\frac{d P}{P}=-\frac{M_{\text {atm }} g}{R T} d z \nonumber \] Інтеграція рівняння (29.5.11), щоб отримати\[\int_{P_{0}}^{P(z)} \frac{d P}{P}=\ln \left(\frac{P(z)}{P_{0}}\right)=-\int_{0}^{z} \frac{M_{\text {atm }} g}{R T} d z=-\frac{M_{\text {atm }} g}{R T} z \nonumber \] експоненціат обидві сторони Рівняння (29.5.12) знайти тиск P (z) в атмосфері як функцію висоти z над поверхнею землі,\[P(z)=P_{0} \exp \left(-\frac{M_{\mathrm{atm}} g}{R T} z\right) \nonumber \]
Приклад 29.2 Ідеальний атмосферний тиск газу
Яке відношення атмосферного тиску при z = 9,0 км до атмосферного тиску на поверхні землі для нашої ідеально-газової атмосфери?
Рішення\[\frac{P(9.0 \mathrm{km})}{P_{0}}=\exp \left(-\frac{\left(28.6 \times 10^{-3} \mathrm{kg} \cdot \mathrm{mol}^{-1}\right)\left(9.8 \mathrm{m} \cdot \mathrm{s}^{-2}\right)}{\left(8.31 \mathrm{J} \cdot \mathrm{K}^{-1} \cdot \mathrm{mol}^{-1}\right)(250 \mathrm{K})}\left(9.0 \times 10^{3} \mathrm{m}\right)\right) = 30 \nonumber \]
Атмосфера Землі
Ми зробили два припущення про атмосферу, що температура була рівномірною і що різні молекули газу були рівномірно змішані. Фактична температура змінюється залежно від конкретного регіону атмосфери. Графік температури як функції висоти показаний на малюнку 29.6.

У тропосфері температура знижується з висотою; земля є основним джерелом тепла, в якому відбувається поглинання інфрачервоного (ІЧ) випромінювання слідовими газами і хмарами, а також відбувається конвекція і провідність теплової енергії. У стратосфері температура зростає з висотою за рахунок поглинання ультрафіолетового (УФ) випромінювання від сонця озоном. У мезосфері температура знижується з висотою. Атмосфера і земля під мезосферою є основним джерелом ІЧ, який поглинається озоном. У термосфері сонце нагріває термосферу за рахунок поглинання рентгенівських променів і УФ киснем. Температура коливається від 500 К до 2000 К в залежності від сонячної активності.
У нижній атмосфері переважає турбулентне змішування, яке не залежить від молекулярної маси. Близько 100 км відбувається як дифузійне, так і турбулентне змішування. Верхній склад атмосфери обумовлений дифузією. Змінюється співвідношення змішування газів і середня молярна маса зменшується в залежності від висоти. Тільки найлегші гази присутні на більш високих рівнях. Змінні компоненти, такі як водяна пара та озон, також впливатимуть на поглинання сонячної радіації та ІЧ-випромінювання від землі. Графік висоти проти середньої молекулярної маси показаний на малюнку 29.7. Щільність чисельності окремих видів і загальна щільність чисельності побудовані на малюнку 29.8.
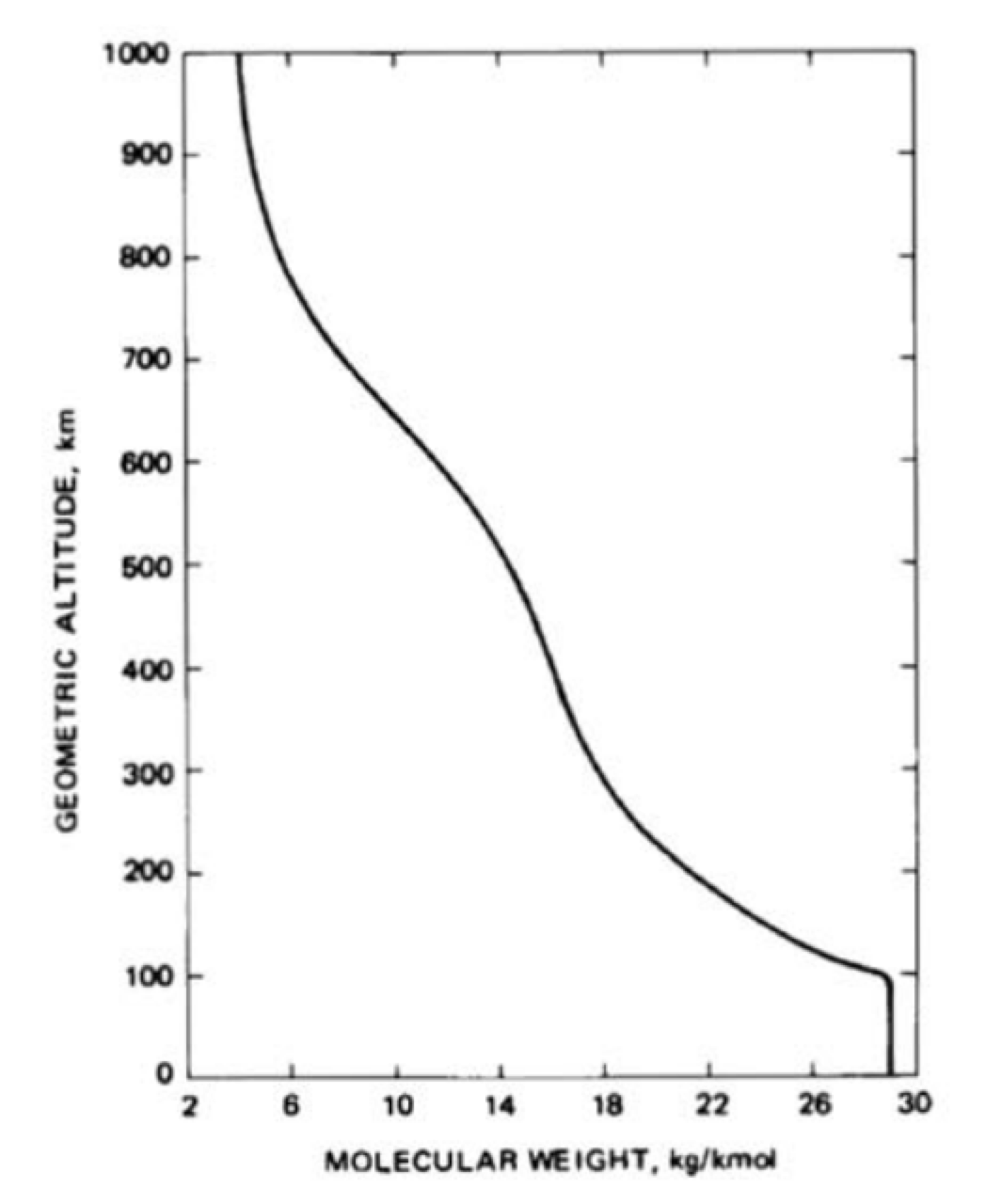

(Зверніть увагу, що у наведеній вище етикетці та підписі до малюнка 29.8 замість більш відповідної «молекулярної маси» або «молярної маси» використовується термін «молекулярна маса».)
