9.5: Конгруенції, розширення та жорсткість
- Page ID
- 77216
Цілі навчання
- Поясніть математичні методи для підходу до різних питань, таких як розширення, обертання та зсув

Цей розділ зосереджений на флуксах збережених кількостей; ми хотіли виключити такі зображення, як малюнок\(\PageIndex{1}\) (1), в яких поява та зникнення світових ліній означало б незбереження таких властивостей, як заряд та масова енергія. Але математичні методи, які ми розробили, виявляються елегантним способом підійти до різних питань, описаних в інших частинок фігури\(\PageIndex{1}\).
Конгруенції
На малюнку\(\PageIndex{1}\) (2) ми маємо розширення. Наприклад, світові лінії можуть представляти галактики, що стають все далі один від одного через космологічне розширення в результаті Великого вибуху. Ми не очікуємо, що лінійки будуть розширюватися або скорочуватися, в тому сенсі, що, хоча лінійка може демонструвати стиснення Лоренца, вона завжди повинна мати однакову довжину у власній рамці відпочинку, якщо вона не була механічно підкреслена або змінена.
Якщо є більше одного просторового виміру, то ми можемо мати обертання, як на малюнку\(\PageIndex{1}\) (3). Ці світові лінії можуть представляти сузір'я орбітальних супутників або фіксованих точок у обертовій лабораторії.
Іншою цікавою можливістю, якщо є більше одного просторового виміру, є зсув, малюнок\(\PageIndex{1}\) (4). Тут прямокутна група з чотирьох частинок стискається в одному напрямку, розширюючись в іншому, щоб зберегти константу закритого\(2\) обсягу.
Для того, щоб обговорити ці можливості, зручно визначити поняття часоподібної конгруентності, яка являє собою сукупність непересічних, плавних, схожих на час світових ліній, об'єднання яких становить всі події в якомусь регіоні простору-часу. Тобто ми «заповнюємо» простор часу нескінченною кількістю світових ліній, щоб між ними не було простору. Це щось на зразок зерна в шматку дерева, або концепція Фарадея про польові лінії, що заповнюють простір, за винятком того, що один з наших\(n + 1\) вимірів схожий на час, і лінії не дозволяють вказувати в напрямках, які лежать поза світловим конусом. Один із способів вказати конгруентність - дати нормований вектор швидкості, який є дотичним до світової лінії, що проходить через будь-яку задану точку.
Приклад\(\PageIndex{1}\): An expanding congruence
Як приклад конгруентності в\(1+1\) розмірах розглянемо множину всіх кривих виду\(x = ae^{bt}\), де\(a\) і\(b\) є додатними константами. Це виглядало б як цифра\(\PageIndex{1}\) (2). Нехай
\[u = \frac{\mathrm{d} x}{\mathrm{d} t} = abe^{bt}\]
вектор швидкості дорівнює
\[v^λ = γ^{-1} (1,u)\]
де фактор\(\gamma ^{-1} = \sqrt{1 - u^2}\) дає правильну нормалізацію\(v^λ v_λ = 1\).
Приклад\(\PageIndex{2}\): A boring congruence
Припустимо, ми замість цього дозволимо конгруентності складатися з безлічі всіх кривих форми\(x = c + ut\), де\(c\) і\(u\) є константами і\(|u| < 1\). Тоді, як і в наведеному вище прикладі,\(v^λ = γ^{-1} (1,u)\). Світові лінії інерційні і паралельні один одному.
Розширення і жорсткість
Протягом решти цієї дискусії ми обмежуємося\(1 + 1\) -мірним випадком, так що обертання і зсув неможливі, і єдине цікаве питання полягає в тому, чи має дана конгруентність розширення. У\(1 + 1\) розмірах конгруентність можна задати, надавши функцію\(u(x,t)\), де, як у прикладах вище,\(u = dx/dt\). Якщо\(u\) постійний, то у нас є приклад\(\PageIndex{2}\), і явно немає розширення. Таким чином, розширення вимагає\(∂u/∂t\) або або\(∂u/∂x\), або обох, бути ненульовим.
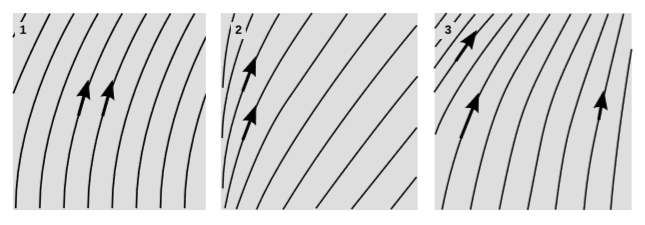
На малюнку\(\PageIndex{1}\) (1) показаний випадок, де\(∂u/∂x = 0\) і\(∂u/∂t \neq 0\). Кожна лінія світу є копією інших, які були зрушені просторово, і два вектори швидкості, показані як стрілки, рівні. Це саме парадокс космічного корабля Белла (розділ 3.9). Хоча горизонтальний інтервал між світовими лініями залишається постійним, як це визначено фіксованою системою відліку, яка використовується для діаграми, спостерігач, що прискорюється разом з однією з частинок, виявить, що вони розширилися одна від одної, тому що лічильники спостерігача мають Lorentz контракт. Це реальне розширення в тому сенсі, що якщо світові лінії є частинками в твердому об'єкті, об'єкт потрапляє під зростаючу напругу.
На малюнку\(\PageIndex{2}\) (2) ми маємо\(∂u/∂t = 0\) і\(∂u/∂x \neq 0\). Світові лінії - це копії один одного, які були зрушені тимчасово. Два вектори швидкості на діаграмі однакові. Всі частинки почали прискорюватися з однієї точки в просторі, але в різний час. Тут явно є розширення, тому що світові лінії стають все далі один від одного.
Припустимо, що ми прискорюємо такий жорсткий предмет, як лінійка. Тоді у нас повинно бути щось на зразок фігури\(\PageIndex{2}\) (3). Щоб уникнути ситуацій, описаних у розділах\(\PageIndex{2}\)\(\PageIndex{2}\) (1) та (2), вектор швидкості повинен змінюватися з обома\(t\) і\(x\); три вектори швидкості на малюнку різні. Коли частинки прискорюються, інтервал між ними Лоренц стискається, так що спостерігач, що прискорюється разом з ними, бачить інтервал як постійний.
Це поняття жорсткого руху в відносності називається Борна ригідність. Жодна фізична речовина, природно, не може бути абсолютно жорстким (Народжений жорстким), бо якби це було, то швидкість, з якою звукові хвилі пройшли в ньому, була б більшою, ніж c Народжена жорсткість може бути досягнута лише за допомогою набору зовнішніх сил, прикладених у всіх точках об'єкта згідно з програмою, яка була запланована заздалегідь. Справжній об'єкт, такий як лінійка, не зберігає власної народженої жорсткості, але з часом він повернеться до свого початкового розміру та форми після того, як зазнав релятивістського прискорення, завдяки власним еластичним властивостям, за умови, що прискорення було досить м'яким, щоб не пошкодити його назавжди. У\(1+1\) розмірах жорсткість Борна еквівалентна відсутності розширення. За\(3 + 1\) розмірами ми також вимагаємо зсуву зсуву.
Математично зрозуміло, що умова зникнення розширення повинна бути вираженою в\(1 + 1\) розмірах з точки зору часткових похідних\(∂u/∂t\) і\(∂u/∂x\), і оскільки ми змогли описати умову незалежним від кадру способом (посилаючись на спостереження, зроблені comoving спостерігач), це також повинно бути те, що ми можемо висловити як скаляр у граматиці індексної гімнастики. Існує тільки один можливий спосіб висловити таку умову, який є
\[∂_a v^a = 0\]
Насправді ми можемо визначити скаляр\(Θ\), званий скалярним розширенням, відповідно до
\[Θ = ∂_a v^a\]
Це визначення справедливо в\(n+1\) розмірах, але в\(1+1\) розмірах воно зводиться до
\[\Theta = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\]
Скаляр розширення інтерпретується як дробова швидкість зміни обсягу набору частинок, що рухаються по світових лініях, визначених конгруентністю, де швидкість зміни визначається щодо\(τ\) належного часу спостерігача, що рухається разом з частинками. Наприклад, космологічне розширення призводить до дробового збільшення відстаней між галактиками,\(∆L/L\) яке за невеликий проміжок часу дорівнює тому\(∆τ\), де\(H_o∆τ\)\(H_o\), звана постійною Хаббла, знаходиться приблизно\(2.3×10^{-18}\; s^{-1}\). Тобто дробова швидкість зміни є\((1/L)dL/dτ = H_o\). Оскільки відстані розширюються у всіх трьох просторових вимірах, дробова швидкість зміни об'єму становить
\[\Theta = \frac{1}{V}\frac{\mathrm{d} V}{\mathrm{d} \tau } = 3H_o\]
У цьому прикладі spacetime не є плаваючою, тому нам доведеться висловити\(Θ\) в терміні коваріантної похідної,\(∇_a\) визначеної в розділі 9.4, а не часткової похідної\(∂a\).
Приклад\(\PageIndex{3}\): A catastrophe
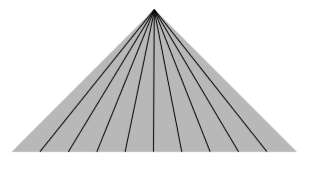
Розглянемо часоподібну конгруентність в\(1+1\) розмірах, визначених\(u = x/t\). Це складається з безлічі всіх інерційних світових ліній, що проходять через початок. Оскільки наше визначення конгруентності вимагає, щоб світові лінії не перетиналися, давайте обмежимося цим прикладом внутрішньою частиною минулого світлового конуса походження,\(|x| < -t\). У нас є Всесвіт, повний нещасних частинок, і всі вони прямують як лемінги до катастрофічного зіткнення. Діаграма просторового часу виглядає як діаграма оптичних променів для формування реального зображення. Обчислення дає несподівано простий результат\(Θ = γ/t\). Бо\(t < 0\), це негативне, що вказує на скорочення, і воно підривається до мінус нескінченності у міру\(t\) наближення\(0\).
їдкі
Верхівка шишки в прикладі\(\PageIndex{3}\) - їдкий. З огляду на набір прямих ліній, що заповнюють простір, виникає їдка, де їх інтенсивність розходиться до нескінченності. Слово означає «горіння», тому що в оптиці їдка світлових променів концентрує енергію і може спалювати речі. Приклад\(\PageIndex{3}\) включає в себе їдкий час, як світові лінії, і «прямі» слід інтерпретувати як значення того, що світові лінії є інерційними.

\(\PageIndex{4}\)На малюнку показані дві каустики, утворені простороподібними лініями для прискореної системи координат, описаної в розділі 7.1. Тут, як це часто буває, їдкі - це не просто точки.
Прикладом із загальної теорії відносності є те, що коли чорна діра утворюється гравітаційним колапсом, їдка утворюється в одній точці набором світлоподібних світових ліній, які входять в горизонт подій із зовнішнього Всесвіту в момент формування горизонту. Якщо з цієї їдкої точки випромінюється промінь світла, він залишається на горизонті подій назавжди, як і всі промені, що випромінюються на горизонті у напрямку назовні в більш пізні часи. Горизонт подій - це такий же набір подій, як об'єднання всіх світлоподібних світових ліній, які входять в горизонт у їдкого. 4
Теорема Герглоца-Нетера в розмірах 1+1
Деякі народжені жорсткі типи руху можливі, а інші - ні, чисто як питання кінематики. Виявляється можливим розігнати стрижень народженим жорстким способом по власній довжині, але, на подив, не представляється можливим, наприклад, щоб сфера залишалася народженою жорсткою при одночасному обертанні і прискорення її центру маси. Можливі типи руху окреслені теоремою, яка називається теоремою Герглоца-Нетера. На відміну від\(3+1\) -мірної версії теореми,\(1+1\) -мірна версія не є ні дивною, ні важко констатувати або довести.
Теорема Герглоца-Нетера в\(1+1\) розмірах: Будь-який жорсткий рух у\(1 + 1\) розмірах однозначно визначається світовою лінією однієї\(W\) точки, за умови, що світова лінія цієї точки є гладкою і схожою на час. Загалом можна лише розширити конгруентність, що описує рух, на деяку околицю\(W\).
Доказ
Щоб уникнути технічних проблем, припускаємо, що «гладкий» означає аналітичний, що трохи послаблює результат. Як обговорювалося вище, нульове розширення еквівалентно тому\(0 = \frac{\partial \gamma }{\partial t} + \frac{\partial (u\gamma )}{\partial x}\), де\((t,x)\) знаходиться будь-який набір координат Мінковського. Це можна викласти в форму\(\frac{\partial u}{\partial x} = f(u) \frac{\partial u}{\partial t}\), де\(f\) рівно для\(-1 < u < 1\) і\(f(0) = 0\). Потрібно довести, що розв'язання цього рівняння з частинними похідними, якщо воно існує, є єдиним заданим\(W\). Ми довільно вибираємо одну подію далі\(W\). За припущенням,\(W\) це час, як в цей момент, тому ми вільні вибирати наші координати Мінковського таким чином, що наша точка знаходиться в спокої в цій події на початку. Так як\(f(0) = 0\), випливає, що за походженням\(∂u/∂x = 0\). Ми можемо аналогічно оцінити вищі похідні\(∂^n u/∂x^n\), і\(u\) тому що гладко ми можемо в цьому обчисленні вільно обмінюватися порядком часткових похідних\(∂x\) і\(∂t\). Це просто показати, що ці вищі похідні також\(∂^n u/∂x^n\) є нулем. Оскільки\(u(x)\) вважається аналітичним, то випливає, що\(u(0,x) = 0\) для всіх\(x\), тобто спостерігач миттєво рухається уздовж\(W\),\(t = 0\) говорить, що всі інші точки знаходяться в стані спокою, а в той час. Але тому, що\(W\) це час, ми завжди можемо знайти деяке\(A\) сусідство з\(W\) таким, що кожна точка одночасно з унікальною подією на\(W\) відповідно до спостерігача на цій події рухається разом з\(W\).\(A\) Тому значення\(u\) визначається скрізь в\(A\), і це завершує доказ того, що конгруентність існує і є унікальною в\(A\).
Зауваження
- \(1 + 1\)-вимірна версія теореми Герглоца-Нетера не є окремим випадком\(3 + 1\) -мірного варіанту. Останнє, як правило, доведено для конгруентності, що заповнює простір, і він виходить з ладу, коли тіло, про яке йде мова, не охоплює обсяг, наприклад, у випадку тонкого стрижня або букви «C».
- Теорему можна посилити, послабивши вимогу гладкості так, що потрібно лише існування другої похідної положення щодо належного часу. 5
- Якщо рух прискорено, то жорсткий рух не можна продовжити на довільну відстань від\(W\). Якщо правильне прискорення\(W\) може бути настільки ж великим, як а, то як в прикладі?? , р.?? , ми очікуємо, що зможемо продовжити жорсткий рух на належну відстань лише таку велику\(c^2/a\), як, де буде їдкий, подібний до тієї, що на малюнку\(\PageIndex{4}\).
Парадокс космічного корабля Белла переглянуто
Парадокс космічного корабля Белла обговорювався в розділі 3.9. У парадоксі два космічних корабля починають прискорюватися одночасно і мають рівні прискорення в кадрі зовнішнього, інерційного спостерігача, внаслідок чого натягнута між ними нитка розривається. Тепер наведемо більш сувору і математично елегантну демонстрацію того ж результату, запропонованого П.Алленом.
Рух нитки по всій її довжині можна описати часомподібної конгруентністю. Якщо нитка не повинна піддаватися ніякому напруженню, то це повинна бути вроджено-жорстка конгруентність. За\(1+1\) -мірною теоремою Герглоца-Нетера конгруентність однозначно визначається рухом однієї з її точок, яку ми приймаємо за задню ракету. Ця конгруентність буває відома. Вона визначається системою прискорених координат (координати Ріндлера), описаної в розділі 7.1. Зникнення скаляра розширення для цієї конгруентності залишається для перевірки читача. Але ця конгруентність складається зі світових ліній, чиї власні прискорення є кожною постійною і всі відрізняються один від одного, і це суперечить опису, наданому в парадоксі Белла, де зазначено, що існує кадр, в якому руху двох кораблів ідентичні, за винятком перекладу. Тому нитка не може рухатися жорстко.
На цьому вирішення парадоксу завершено, але в якості наочного прикладу ми наведемо явний розрахунок скаляра розширення для конгруентності, яку можна було б найбільш природно уявити під описом парадоксу. Це дається\((x + c)^2 = 1 + t^2\). Для заданого значення параметра\(c\) отримаємо прискорюючу світову лінію. (Його правильне прискорення\(a = 1\) буває постійним, хоча це не потрібно для цілей обговорення парадоксу.) Кожна світова лінія починається в стані спокою\(t = 0\), і кожна з них має однакове прискорення в будь-який момент\(t\). Вибравши будь-які два різних значення\(c\) як кінцевих точок потоку, ми отримуємо буквальну ситуацію, описану в парадоксі.
Неявна диференціація дає\(u = \frac{t}{\sqrt{1 + t^2}}\). Зараз алгебра стає трохи брудною, тому я використовував систему комп'ютерної алгебри з відкритим вихідним кодом Maxima. Наступна програма, яка повинна бути досить читабельною без попереднього знання синтаксису Maxima, обчислює тензор розширення:
- u: т/кв (1+т ^ 2);
- гамма:1/квадратний (1-u ^ 2);
- тета:різниця (гамма, т) +диф (u*гамма, х);
- є (дорівнює (тета, гамма*u^2/t));
У третьому рядку виводиться складний вираз\(Θ\), для якого четвертий рядок показує, можна спростити\(γu^2/t\). Це позитивно для\(t > 0\), що показує, що нитка змушена розширюватися. Зверніть увагу, що хоча розрахунок проводився в певному наборі координат, релятивістський скаляр, такий як\(Θ\) має координатно-незалежне значення. Посилання на ту чи іншу систему координат або систему відліку відбувається тільки при початковому визначенні конгруентності, яке визначається для того, щоб змоделювати ситуацію, описану в парадоксі, який викладається в терміні конкретного зовнішнього спостерігача.
